Weiyu Luo
School of Mathematics and Statistics, Guangxi Normal University, Guilin, China.
DOI: 10.4236/jamp.2024.121008   PDF    HTML   XML   38 Downloads   172 Views   Citations

Abstract

In this article, new visual and intuitive interpretations of Lorentz transformation and Einstein velocity addition are given. We first obtain geometric interpretations of isometries of vertical projection model of hyperbolic space, which are the analogues of the geometric construction of inversions with respect to a circle on the complex plane. These results are then applied to Lorentz transformation and Einstein velocity addition to obtain geometric illustrations. We gain new insights into the relationship between special relativity and hyperbolic geometry.

Keywords

Lorentz Transformation, Einstein Velocity Addition, Hyperbolic Space

Share and Cite:

1. Introduction

Einstein’s special relativity theory is one of the foundation blocks of modern theoretical physics [1] [2] [3] and its rich mathematical structures have been intensively studied [4] [5] . The composition law for velocities in special relativity is intimately related to hyperbolic geometry, as was first pointed out by Sommerfeld [6] , Varičak [7] [8] , Robb [9] , and Borel [10] . More recently, the subject was elaborated on by Ungar [11] [12] . In light of an all-important observation described in Theorem 2.1 below, which involves geometric description of isometries in hyperbolic space, we obtain new intuitive understandings of Lorentz transformation and relativistic addition of velocities in special relativity. Though Minkowski had given a geometric meaning of Lorentz transformation [1] , ours seems to be more geometrically satisfactory.

The basic idea of this article stems from the geometric construction of inversions with respect to a circle on the complex plane, that is, given a point P inside a circle C, the inversion point of P with respect to the circle C can be obtained by geometric construction with ruler and compass as follows: Starting from the center O of the circle C and passing through P, create a ray OP; draw the perpendicular line of OP through P, which intersects with C at point Q; draw the tangent of C through Q, then the intersection point of this tangent with the ray OP is the inversion point of P. Since inversions, which are isometries of conformal ball model of hyperbolic space, have the above geometric constructions, it is interesting to establish the analogous geometric description of isometries of other hyperbolic models. We succeed in finding out the analogous geometric description of isometries of vertical projection model of hyperbolic space (Theorem 2.1) and, furthermore, use it to obtain geometric illustrations of Lorentz transformation and Einstein velocity addition because they can all be recognized as isometries of hyperbolic space.

2. New Geometric Interpretation of Isometries in Vertical Projection Model of Hyperbolic Space

Let n be a positive integer. Let ${ℝ}^{n\mathrm{,1}}=\left({ℝ}^{n+1}\mathrm{,}\text{d}{s}_{{ℝ}^{n\mathrm{,1}}}^2=-\text{d}{x}_0^2+\text{d}{x}_1^2+\cdots +\text{d}{x}_n^2\right)$ be the Lorentzian n+1-space. For $x=\left(x_1\mathrm{,}\cdots \mathrm{,}{x}_n\right)\in {ℝ}^n$ , $y=\left(y_1\mathrm{,}\cdots \mathrm{,}{y}_n\right)\in {ℝ}^n$ , denote $x\cdot y\mathrm{<mo>\; :\; </mo>}=x_1{y}_1+\cdots +x_n{y}_n$ and ${\left|x\right|}^2=x\cdot x$ . Notations $\cdot$ and $\times$ signify the usual dot (scalar) and cross (vector) product between two vectors throughout. Let c be a positive number (or the speed of light). The hyperboloid $H_{+}^n\left(c\right)\mathrm{<mo>\; :\; </mo>}=\left\{\left(x_0\mathrm{,}x\right)=\left(x_0\mathrm{,}{x}_1\mathrm{,}\cdots \mathrm{,}{x}_n\right)\in {ℝ}^{n+1}\mathrm{<mo>\; |\; </mo>}-x_0^2+x_1^2+\cdots +x_n^2=-c^2\text{and}{x}_0>0\right\}$ . The open c-ball in ${ℝ}^n$ is $B_c^n\mathrm{<mo>\; :\; </mo>}=\left\{\left(x_1,\cdots ,x_n\right)\in {ℝ}^n|x_1^2+\cdots +x_n^2<c^2\right\}$ . We use the following four models of hyperbolic n-space:

1) Hyperboloid model:

${ℍ}_h^n\left(c\right)\mathrm{<mo>\; :\; </mo>}=\left(H_{+}^n\left(c\right)\mathrm{,}\text{d}{s}_{{ℍ}_h^n\left(c\right)}^2={\text{d}{s}_{{ℝ}^{n\mathrm{,1}}}^2|}_{H_{+}^n\left(c\right)}\right)\mathrm{,}$

2) Conformal ball model:

${ℍ}_c^n\left(c\right)\mathrm{<mo>\; :\; </mo>}=\left(B_c^n\mathrm{,}\text{d}{s}_{{ℍ}_c^n\left(c\right)}^2=\frac{4}{{\left(1-\frac{{\left|x\right|}^2}{c^2}\right)}^2}\left(\text{d}{x}_1^2+\cdots +\text{d}{x}_n^2\right)\right)\mathrm{,}$

3) Projective model:

${ℍ}_p^n\left(c\right)\mathrm{<mo>\; :\; </mo>}=\left(B_c^n\mathrm{,}\text{d}{s}_{{ℍ}_p^n\left(c\right)}^2=\frac{c^2}{c^2-{\left|x\right|}^2}{\left(\text{d}{x}_1+\cdots +\text{d}{x}_n\right)}^2+\frac{c^2}{{\left(c^2-{\left|x\right|}^2\right)}^2}{\left(x_1\text{d}{x}_1+\cdots +x_n\text{d}{x}_n\right)}^2\right)\mathrm{,}$

4) Vertical projection model (abbreviated as VP model):

${ℍ}_{vp}^n\left(c\right)\mathrm{<mo>\; :\; </mo>}=\left({ℝ}^n\mathrm{,}\text{d}{s}_{{ℍ}_{vp}^n\left(c\right)}^2=\text{d}{x}_1^2+\cdots +\text{d}{x}_n^2-\frac{1}{c^2+{\left|x\right|}^2}{\left(x_1\text{d}{x}_1+\cdots +x_n\text{d}{x}_n\right)}^2\right)\mathrm{.}$

The following natural isometries among these models are needed below:

Remark 2.1. From the isometry ${\phi }_{41}$ , we know that the vertical projection model is just the vertical projection of the hyperboloid model, that’s why we named it vertical projection model (VP model for short). We will see that the vertical projection model is particularly suitable to express the relations in special relativity.

We first introduce some isometries in conformal ball model ${ℍ}_c^n\left(c\right)$ . Let:

$T_a\left(x\right)\mathrm{<mo>\; :\; </mo>}=\frac{\left(1-\frac{1}{c^2}{\left|a\right|}^2\right)x-\left(1+\frac{1}{c^2}{\left|x\right|}^2-\frac{2}{c^2}a\cdot x\right)a}{1-\frac{2}{c^2}a\cdot x+\frac{1}{c^4}{\left|a\right|}^2{\left|x\right|}^2}\mathrm{,}$ (2.1)

which is the analogue of the mapping $z\to \left(z-a\right)/\left(1-\bar{a}z\right)$ on the unit disk of complex plane. This mapping $T_a\left(x\right)$ is of fundamental importance to us, because its physical contents are Lorentz boost and Einstein velocity addition as can be seemed in Sections 3 and 4.

Let $S\left(a\mathrm{,}r\right)$ denotes a sphere with center $a$ and radius r. The inversion with respect to $S\left(a\mathrm{,}r\right)$ is the mapping:

$\begin{array}{l}{i}_{S\left(a\mathrm{,}r\right)}\mathrm{<mo>\; :\; </mo>}{ℝ}^n\backslash \left\{a\right\}\to {ℝ}^n\backslash \left\{a\right\}\\ x\mapsto a+\frac{r^2}{{\left|x-a\right|}^2}\left(x-a\right)\mathrm{.}\end{array}$ (2.2)

Let $r_a$ be the reflection with respect to the hyperplane $a\cdot x=0$ , that is:

$r_a\left(x\right)=x-2\frac{x\cdot a}{a\cdot a}a\mathrm{.}$ (2.3)

For $a\in {ℍ}_c^n\left(c\right)\backslash \left\{0\right\}$ , $S\left(\frac{c^2}{{\left|a\right|}^2}a\mathrm{,}\frac{c\sqrt{c^2-{\left|a\right|}^2}}{\left|a\right|}\right)$ is the unique sphere perpendicular to $S\left(0\mathrm{,}c\right)$ , whose center lies on the ray $\stackrel{\leftarrow }{0a}$ , and the inversion with respect to which sends $a$ to the origin $0$ . Denote the isometry $i_{S\left(\frac{c^2}{{\left|a\right|}^2}a\mathrm{,}\frac{c\sqrt{c^2-{\left|a\right|}^2}}{\left|a\right|}\right)}\left(x\right)$ as $i_a\left(x\right)$ . $i_{S\left(a\mathrm{,}r\right)}^2=1$ , $r_a^2=1$ .

$T_a\left(x\right)=r_a\circ i_a\left(x\right)\mathrm{,}a\mathrm{,}x\in {ℍ}_c^n\left(c\right)\mathrm{.}$ (2.4)

Since $i_a\left(x\right)$ and $r_a$ are isometries of ${ℍ}_c^n\left(c\right)$ , $T_a\left(x\right)$ are also isometries of ${ℍ}_c^n\left(c\right)$ by (2.4).

Recall that k-dimensional totally geodesic submanifolds in hyperbolic space are called k-planes. It is well known that spheres of dimension k that meet the boundary orthogonally and k-dimensional vector subspaces represent totally geodesic hyperbolic k-planes in ${ℍ}_c^n\left(c\right)$ . Especially, $\left(n-1\right)$ -planes in ${ℍ}_c^n\left(c\right)$ are $\left(n-1\right)$ -dimensional vector subspaces and spheres of the form: $S\left(\frac{c^2}{{\left|a\right|}^2}a\mathrm{,}\frac{c\sqrt{c^2-{\left|a\right|}^2}}{\left|a\right|}\right)$ , $a\in {ℍ}_c^n\left(c\right)\backslash \left\{0\right\}$ .

In the subsequent, we describe the above isometries in vertical projection model ${ℍ}_{vp}^n\left(c\right)$ .

Proposition 2.1. 1) $\left(n-1\right)$ -planes in VP model ${ℍ}_{vp}^n\left(c\right)$ are $\left(n-1\right)$ -dimensional vector subspaces and hyperboloid of the form

$H_a\mathrm{<mo>\; :\; </mo>}=\left\{x\in {ℝ}^n\mathrm{<mo>\; |\; </mo>}\sqrt{1+\frac{{\left|x\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot x}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}-1}=0\right\}$ , $a\in {ℍ}_{vp}^n\left(c\right)\backslash \left\{0\right\}$ . Furthermore, the k-planes ( $1\le k<n$ ) in ${ℍ}_{vp}^n\left(c\right)$ are the nonempty intersection of $\left(n-1\right)$ -planes with $\left(k+1\right)$ -dimensional vector subspaces.

2) In ${ℍ}_{vp}^n\left(c\right)$ , the inversion with respect to $H_a$ , denoted by $i_a^{vp}\left(x\right)$ , is the mapping:

$i_a^{vp}\left(x\right)=x+\left(\sqrt{1+\frac{{\left|x\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot x}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}-1}\right)a\mathrm{,}a\in {ℍ}_{vp}^n\left(c\right)\backslash \left\{0\right\}\mathrm{,}x\in {ℍ}_{vp}^n\left(c\right)\mathrm{.}$ (2.5)

3) The corresponding isometry in ${ℍ}_{vp}^n\left(c\right)$ of $T_a\left(x\right)$ (see (2.1)), denoted as $T_a^{vp}\left(x\right)$ , is:

$T_a^{vp}\left(x\right)=x-\left(\sqrt{1+\frac{{\left|x\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot x}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}+1}\right)a\mathrm{,}a\mathrm{,}x\in {ℍ}_{vp}^n\left(c\right)\mathrm{.}$ (2.6)

4)

$T_a^{vp}\left(x\right)=r_a\circ i_a^{vp}\left(x\right)\mathrm{,}a\in {ℍ}_{vp}^n\left(c\right)\backslash \left\{0\right\}\mathrm{,}x\in {ℍ}_{vp}^n\left(c\right)\mathrm{.}$ (2.7)

Proof: The isometry ${\phi }_{42}$ maps $\left(n-1\right)$ -plane $S\left(\frac{c^2}{{\left|a\right|}^2}a\mathrm{,}\frac{c\sqrt{c^2-{\left|a\right|}^2}}{\left|a\right|}\right)$ , $a\in {ℍ}_c^n\left(c\right)\backslash \left\{0\right\}$ in ${ℍ}_c^n\left(c\right)$ onto $\left(n-1\right)$ -plane in ${ℍ}_{vp}^n\left(c\right)$ , which is a sheet of hyperboloid given by:

$H_a\mathrm{<mo>\; :\; </mo>}\sqrt{1+\frac{{\left|x\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot x}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}-1}=\mathrm{0,}a\in {ℍ}_{vp}^n\left(c\right)\backslash \left\{0\right\}\mathrm{.}$

In ${ℍ}_{vp}^n\left(c\right)$ , the inversion with respect to $H_a$ is:

$\begin{array}{c}{i}_a^{vp}\left(x\right)={\phi }_{24}^{-1}\circ i_{{\phi }_{24}\left(a\right)}\circ {\phi }_{24}\left(x\right)\\ =x+\left(\sqrt{1+\frac{{\left|x\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot x}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}-1}\right)a\mathrm{,}a\in {ℍ}_{vp}^n\left(c\right)\backslash \left\{0\right\}\mathrm{,}x\in {ℍ}_{vp}^n\left(c\right)\mathrm{.}\end{array}$

$T_a^{vp}\left(x\right)={\phi }_{24}^{-1}\circ T_{{\phi }_{24}\left(a\right)}\circ {\phi }_{24}\left(x\right)=x-\left(\sqrt{1+\frac{{\left|x\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot x}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}+1}\right)a\mathrm{.}$

n

These isometries $i_a^{vp}\left(x\right)$ and $T_a^{vp}\left(x\right)$ in VP model ${ℍ}_{vp}^n\left(c\right)$ have the following quite clear geometric descriptions, which are analogous to the geometric construction of inversion on Euclidean space ${ℝ}^n$ .

Theorem 2.1 (Geometric meaning of $i_a^{vp}\left(x\right)$ and $T_a^{vp}\left(x\right)$ ) 1) The image point $i_a^{vp}\left(A\right)$ of $A\in \left\{x\in {ℝ}^n\mathrm{<mo>\; |\; </mo>}\sqrt{1+\frac{{\left|x\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot x}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}-1}<0\right\}$ can be drawn as follows (Figure 1): Make a sphere S with center $0$ and radius $\left|\stackrel{\leftarrow }{0A}\right|$ , whose intersection with hyperboloid $H_a$ is a $\left(n-2\right)$ -sphere, and the hyperplane on which the intersection $\left(n-2\right)$ -sphere lies is denoted as $\Pi$ . Through $A$ , we draw a line that is parallel to the vector $\stackrel{\leftarrow }{0a}$ . This line intersects the hyperplane $\Pi$ at $B$ . Extend the vector $\stackrel{\leftarrow }{AB}$ by $\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}+1$ times, we get a vector $\stackrel{\leftarrow }{AC}$ , then $C=i_a^{vp}\left(A\right)$ .

2) Furthermore, the symmetric point of $C$ with respect to the vector subspace perpendicular to $\stackrel{\leftarrow }{0a}$ is $T_a^{vp}\left(A\right)$ (Figure 2).

Proof: A direct calculation shows that:

$\Pi \mathrm{<mo>\; :\; </mo>}\sqrt{1+\frac{{\left|A\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot x}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}-1}=\mathrm{0\; <mo>\; ;\; </mo>}$

$B=A+\left(\sqrt{1+\frac{{\left|A\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot A}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}-1}\right)\frac{a}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}+1}\mathrm{<mo>\; ;\; </mo>}$

$\stackrel{\leftarrow }{AB}=\left(\sqrt{1+\frac{{\left|A\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot A}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}-1}\right)\frac{a}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}+1}\mathrm{<mo>\; ;\; </mo>}$

$C=A+\left(\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}+1\right)\stackrel{\leftarrow }{AB}=A+\left(\sqrt{1+\frac{{\left|A\right|}^2}{c^2}}-\frac{\frac{1}{c^2}a\cdot A}{\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}-1}\right)a=i_a^{vp}\left(A\right)\mathrm{.}$

By (2.7), $T_a^{vp}\left(A\right)=r_a\circ i_a^{vp}\left(A\right)=r_a\left(C\right)$ , so the reflection of $C$ with respect to the vector subspace perpendicular to $\stackrel{\leftarrow }{0a}$ is $T_a^{vp}\left(A\right)$ .n

Remark 2.2. It is worth pointing out that the geometric interpretation of inversion given in Theorem 2.1 survives only in vertical projection model of hyperbolic space. It can’t implement in other models of hyperbolic space. It has some interesting geometric features: the line $A{i}_a^{vp}\left(A\right)$ is parallel to the line $0a$ , in particular, $i_a^{vp}\left(x\right)$ and $T_a^{vp}\left(x\right)$ map every parallel line of $0a$ onto itself; the scale factor $\sqrt{1+\frac{{\left|a\right|}^2}{c^2}}+1$ is a constant.

In order to clarify the relation of Theorem 2.1 with special relativity, we introduce the notion of addition on hyperbolic space ${ℍ}^n\left(c\right)$ (we suppress the subscript here) using triangular rule, parallel transport and exponential map. For curve $\gamma \mathrm{<mo>\; :\; </mo>}\left[a\mathrm{,}b\right]\to {ℍ}^n\left(c\right)$ , let $P^{\gamma }\mathrm{<mo>\; :\; </mo>}{T}_{\gamma \left(a\right)}{ℍ}^n\left(c\right)\to T_{\gamma \left(b\right)}{ℍ}^n\left(c\right)$ be the parallel transport isomorphism. For $x\in {ℍ}^n\left(c\right)$ , let ${\exp }_x\mathrm{<mo>\; :\; </mo>}{T}_x{ℍ}^n\left(c\right)\to {ℍ}^n\left(c\right)$ be the exponential map at $x$ , which is a diffeomorphism. For $u\mathrm{,}v\in {ℍ}^n\left(c\right)$ , we denote the unique oriented geodesic segment joining $u$ to $v$ by $\stackrel{\leftarrow }{uv}$ . Let $0$ be the center point of ${ℍ}^n\left(c\right)$ .

Definition 2.1. For $u\mathrm{,}v\in {ℍ}^n\left(c\right)$ , the addition of $u$ and $v$ is $u\#v:={\exp }_u\circ P^{\stackrel{\leftarrow }{0u}}\circ {\exp }_0^{-1}\left(v\right)$ . For $\lambda \in ℝ$ and $u\in {ℍ}^n\left(c\right)$ , scalar multiplication is $\lambda \odot u\mathrm{<mo>\; :\; </mo>}={\exp }_0\left[\lambda {\exp }_0^{-1}\left(u\right)\right]$ .

Remark 2.3. These are the analogues of addition and scalar multiplication on Euclidean space, but the triple $\left({ℍ}^n\left(c\right),\#\mathrm{,}\odot \right)$ is not a vector space but actually form a so-called Gyrovector space (for definition see [11] [12] ).

Introduce the hyperbolic translation in conformal ball model ${ℍ}_c^n\left(c\right)$ ,

for $a\in {ℍ}_c^n\left(c\right)$ , ${\tau }_a\left(x\right)=\frac{\left(1-\frac{1}{c^2}{\left|a\right|}^2\right)x+\left(1+\frac{1}{c^2}{\left|x\right|}^2+\frac{2}{c^2}a\cdot x\right)a}{1+\frac{2}{c^2}a\cdot x+\frac{1}{c^4}{\left|a\right|}^2{\left|x\right|}^2}=T_{-a}\left(x\right)$ (see (2.1)), (2.8)

which is an isometry of ${ℍ}_c^n\left(c\right)$ by Formula (2.4) (see [13] ).

Lemma 2.1. In ${ℍ}_c^n\left(c\right)$ , we have:

${\left(\text{d}{\tau }_u\right)}_0=P^{\stackrel{\leftarrow }{0u}}\mathrm{.}$ (2.9)

Proof: By direct calculation, we have:

${\left(\text{d}{\tau }_u\right)}_0=\left(1-\frac{{\left|u\right|}^2}{c^2}\right)\text{d}x\mathrm{.}$

On the other hand, $\text{d}{s}_{{ℍ}_c^n\left(c\right)}^2={\displaystyle {\sum }_{1\le i\mathrm{,}j\le n}}{g}_{ij}\text{d}{x}_i\otimes \text{d}{x}_j=\frac{4}{{\left(1-\frac{{\left|x\right|}^2}{c^2}\right)}^2}\left(\text{d}{x}_1^2+\cdots +\text{d}{x}_n^2\right)$ . The parallel transport vector field $X\left(t\right)=\left(X^1\left(t\right)\mathrm{,}\cdots \mathrm{,}{X}^n\left(t\right)\right)$ along curve $\stackrel{\leftarrow }{0u}\mathrm{<mo>\; :\; </mo>}\gamma \left(t\right)=ut\mathrm{,}0\le t\le 1$ satisfies:

$\frac{\text{d}{X}^k}{\text{d}t}\left(t\right)+{\displaystyle \underset{1\le i\mathrm{,}j\le n}{\sum }}\left({\Gamma }_{ij}^k\circ \gamma \right){\stackrel{\dot{}}{\gamma }}^i\left(t\right)X^j\left(t\right)=\mathrm{0,}1\le k\le n\mathrm{,}$ (2.10)

where the Christoffel symbol:

${\Gamma }_{ij}^k=\frac{1}{2}{\displaystyle \underset{1\le l\le n}{\sum }}{g}^{kl}\left(\frac{\partial g_{li}}{\partial x_j}+\frac{\partial g_{lj}}{\partial x_i}-\frac{\partial g_{ij}}{\partial x_l}\right)=\frac{2}{c^2-{\left|x\right|}^2}\left(x_j{\delta }_{ki}+x_i{\delta }_{kj}-x_k{\delta }_{ij}\right)\mathrm{.}$

The unique solution of Equation (2.10) for initial condition $X\left(0\right)=w$ is $X\left(t\right)=\left(1-\frac{{\left|u\right|}^2}{c^2}{t}^2\right)w$ . Hence, also:

$P^{\stackrel{\leftarrow }{0u}}=\left(1-\frac{{\left|u\right|}^2}{c^2}\right)\text{d}x\mathrm{.}$

n

Proposition 2.2. The explicit addition formulas of the above four models are as follows:

1) Conformal ball model: for $u\mathrm{,}v\in {ℍ}_c^n\left(c\right)$ ,

$u{\#}_{c}v=\frac{\left(1-\frac{1}{c^2}{\left|u\right|}^2\right)v+\left(1+\frac{1}{c^2}{\left|v\right|}^2+\frac{2}{c^2}u\cdot v\right)u}{1+\frac{2}{c^2}u\cdot v+\frac{1}{c^4}{\left|u\right|}^2{\left|v\right|}^2}\mathrm{.}$ (2.11)

2) Hyperboloid model: for $U=\left(u_0\mathrm{,}u\right)\in {ℍ}_h^n\left(c\right)\mathrm{,}V=\left(v_0\mathrm{,}v\right)\in {ℍ}_h^n\left(c\right)$ ,

$U{\#}_{h}V=\left(\frac{u_0{v}_0+u\cdot v}{c}\mathrm{,}\frac{v_0}{c}u+v+\left(\frac{u_0}{c}-1\right)\frac{u\cdot v}{{\left|u\right|}^2}u\right)\mathrm{.}$ (2.12)

3) Projective model: for $u\mathrm{,}v\in {ℍ}_p^n\left(c\right)$ ,

$u{\#}_{p}v=\frac{1}{1+\frac{u\cdot v}{c^2}}\left\{u+\sqrt{1-\frac{{\left|u\right|}^2}{c^2}}v+\frac{1}{c^2}\frac{1}{1+\sqrt{1-\frac{{\left|u\right|}^2}{c^2}}}\left(u\cdot v\right)u\right\}\mathrm{.}$ (2.13)

4) Vertical projection model: for $u\mathrm{,}v\in {ℍ}_{vp}^n\left(c\right)$ ,

$u{\#}_{vp}v=u+v+\left\{\frac{1}{\sqrt{1+\frac{{\left|u\right|}^2}{c^2}}+1}\frac{u\cdot v}{c^2}+\sqrt{1+\frac{{\left|v\right|}^2}{c^2}}-1\right\}u\mathrm{.}$ (2.14)

Proof: 1) Since ${\tau }_u\left(x\right)$ is an isometry of ${ℍ}_c^n\left(c\right)$ (see [13] ), it maps geodesic to geodesic, so:

${\tau }_u\circ {\exp }_0={\exp }_u\circ {\left(\text{d}{\tau }_u\right)}_0\mathrm{.}$ (2.15)

Hence, by Definition 2.1 and Lemma 2.1,

$u{\#}_{c}v={\exp }_u\circ P^{\stackrel{\leftarrow }{0u}}\circ {\exp }_0^{-1}\left(v\right)={\exp }_u\circ {\left(\text{d}{\tau }_u\right)}_0\circ {\exp }_0^{-1}\left(v\right)={\tau }_u\circ {\exp }_0\circ {\exp }_0^{-1}\left(v\right)={\tau }_u\left(v\right)\mathrm{.}$

2) $U{\#}_{h}V={\phi }_{21}^{-1}\left[{\phi }_{21}\left(U\right){\#}_c{\phi }_{21}\left(V\right)\right]=\left(\frac{u_0{v}_0+u\cdot v}{c}\mathrm{,}\frac{v_0}{c}u+v+\left(\frac{u_0}{c}-1\right)\frac{u\cdot v}{{\left|u\right|}^2}u\right).$

3) $\begin{array}{c}u{\#}_{p}v={\phi }_{13}^{-1}\left[{\phi }_{13}\left(u\right){\#}_h{\phi }_{13}\left(v\right)\right]\\ =\frac{1}{1+\frac{u\cdot v}{c^2}}\left\{u+\sqrt{1-\frac{{\left|u\right|}^2}{c^2}}v+\frac{1}{c^2}\frac{1}{1+\sqrt{1-\frac{{\left|u\right|}^2}{c^2}}}\left(u\cdot v\right)u\right\}.\end{array}$

4) $\begin{array}{c}u{\#}_{vp}v={\phi }_{24}^{-1}\left[{\phi }_{24}\left(u\right){\#}_c{\phi }_{24}\left(v\right)\right]\\ =u+v+\left\{\frac{1}{\sqrt{1+\frac{{\left|u\right|}^2}{c^2}}+1}\frac{u\cdot v}{c^2}+\sqrt{1+\frac{{\left|v\right|}^2}{c^2}}-1\right\}u.\end{array}$

n

Remark 2.4.

$T_a\left(x\right)=\left(-a\right){\#}_{c}x={\tau }_{-a}\left(x\right)\mathrm{,}{T}_a^{vp}\left(x\right)=\left(-a\right){\#}_{vp}x\mathrm{.}$ (2.16)

In later sections, we shall apply the established results of hyperbolic space in this section to special relativity.

3. Geometric Illustration of Lorentz Transformation

Suppose that a reference frame S' is moving relative to a similarly oriented frame S with velocity $u=\left(u_1\mathrm{,}{u}_2\mathrm{,}{u}_3\right)$ ; and suppose further that they both take the origin of their coordinate systems to be the event at which they pass each other. The standard 4-dimensional Lorentz boost relates space-time coordinates $t^{\prime }\mathrm{,}{x^{\prime }}_1\mathrm{,}{x^{\prime }}_2\mathrm{,}{x^{\prime }}_3$ of frame S' and $t\mathrm{,}{x}_1\mathrm{,}{x}_2\mathrm{,}{x}_3$ of frame S is [2] [3] :

${\left(c{t}^{\prime }{x^{\prime }}_1{x^{\prime }}_2{x^{\prime }}_3\right)}^{\text{T}}=B\left(u\right){\left(ct{x}_1{x}_2{x}_3\right)}^{\text{T}}\mathrm{,}$ (3.1)

(the exponent T indicates transposition) where:

$B\left(u\right)\mathrm{<mo>\; :\; </mo>}=\left(\begin{array}{cccc}{\gamma }_u& -{\gamma }_u{u}_1/c& -{\gamma }_u{u}_2/c& -{\gamma }_u{u}_3/c\\ -{\gamma }_u{u}_1/c& 1+\left({\gamma }_u-1\right)\frac{u_1{u}_1}{{\left|u\right|}^2}& \left({\gamma }_u-1\right)\frac{u_1{u}_2}{{\left|u\right|}^2}& \left({\gamma }_u-1\right)\frac{u_1{u}_3}{{\left|u\right|}^2}\\ -{\gamma }_u{u}_2/c& \left({\gamma }_u-1\right)\frac{u_2{u}_1}{{\left|u\right|}^2}& 1+\left({\gamma }_u-1\right)\frac{u_2{u}_2}{{\left|u\right|}^2}& \left({\gamma }_u-1\right)\frac{u_2{u}_3}{{\left|u\right|}^2}\\ -{\gamma }_u{u}_3/c& \left({\gamma }_u-1\right)\frac{u_3{u}_1}{{\left|u\right|}^2}& \left({\gamma }_u-1\right)\frac{u_3{u}_2}{{\left|u\right|}^2}& 1+\left({\gamma }_u-1\right)\frac{u_3{u}_3}{{\left|u\right|}^2}\end{array}\right)$ (3.2)

and the gamma factor ${\gamma }_u$ is defined by:

${\gamma }_u=\frac{1}{\sqrt{1-\frac{{\left|u\right|}^2}{c^2}}}\mathrm{.}$ (3.3)

When $u=\left(u_1\mathrm{,0,0}\right)$ , the corresponding matrix:

$\left(\begin{array}{cccc}{\gamma }_u& -{\gamma }_u{u}_1/c& 0& 0\\ -{\gamma }_u{u}_1/c& {\gamma }_u& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$ (3.4)

is often called a boost in the $x^1$ -direction.

$B\left(u\right)=A^{\text{T}}\left(\begin{array}{cccc}{\gamma }_u& -{\gamma }_u\left|u\right|/c& 0& 0\\ -{\gamma }_u\left|u\right|/c& {\gamma }_u& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)A\mathrm{,}$ (3.5)

where A is the unimodular orthogonal matrix (rotation in real world space):

$A\mathrm{<mo>\; :\; </mo>}=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& \frac{u_1}{\left|u\right|}& \frac{u_2}{\left|u\right|}& \frac{u_3}{\left|u\right|}\\ 0& \frac{-u_2}{\sqrt{u_1^2+u_2^2}}& \frac{u_1}{\sqrt{u_1^2+u_2^2}}& 0\\ 0& \frac{-u_1{u}_3}{\sqrt{u_1^2+u_2^2}\left|u\right|}& \frac{-u_2{u}_3}{\sqrt{u_1^2+u_2^2}\left|u\right|}& \frac{\sqrt{u_1^2+u_2^2}}{\left|u\right|}\end{array}\right)\mathrm{.}$ (3.6)

Lorentz boost, which acts on the 4-dimensional Minkowski space-time ${ℝ}^{\mathrm{3,1}}$ , can be viewed as an action on the 3-dimensional real world space ${ℝ}^3$ by the following procedure.

Since $x_1^2+x_2^2+x_3^2-{\left(ct\right)}^2$ is Lorentz invariant, Lorentz boost (3.1) maps the hyperboloid $H_{+}^3\left(c\right):=\left\{\left(ct,x_1,x_2,x_3\right)\in {ℝ}^4|-{\left(ct\right)}^2+x_1^2+x_2^2+x_3^2=-c^2,t>0\right\}$ in Minkowski space-time ${ℝ}^{\mathrm{3,1}}$ 1-1 onto itself. Furthermore, since Lorentz transformations are linear and the hyperboloid $H_{+}^3\left(c\right)$ contains a basis of the Minkowski space-time ${ℝ}^{\mathrm{3,1}}$ , the Lorentz boost (3.1) is completely determine by its action on the hyperboloid $H_{+}^3\left(c\right)$ . Denote $ct$ as $x_0$ and use the notations in Section 2. We see that the Lorentz boost (3.1) acts as an isometry on hyperboloid model ${ℍ}_h^3\left(c\right)$ . ${ℍ}_h^3\left(c\right)$ is isometric to VP model ${ℍ}_{vp}^3\left(c\right)$ under the vertical projection ${\phi }_{41}$ . Thus under ${\phi }_{41}$ , Lorentz boost corresponds to an isometry on ${ℍ}_{vp}^3\left(c\right)$ . From the physical point of view, it is more natural to deal with physical objects such as Lorentz boost on VP model ${ℍ}_{vp}^3\left(c\right)$ , because the underlying space of ${ℍ}_{vp}^3\left(c\right)$ is the real world space ${ℝ}^3$ . Also, mathematically, Lorentz boost is simplified when converting to the VP model ${ℍ}_{vp}^3\left(c\right)$ , as can be seen from the following theorem.

Theorem 3.1. When transitioning to the VP model ${ℍ}_{vp}^3\left(c\right)$ , the Lorentz boost (3.1) becomes

$X^{\prime }=X+\left(-\sqrt{1+\frac{{\left|X\right|}^2}{c^2}}+\frac{\frac{1}{c^2}U\cdot X}{\sqrt{1+\frac{{\left|U\right|}^2}{c^2}}+1}\right)U=\mathrm{<mo>\; :\; </mo>}{L}_U\left(X\right)\mathrm{,}$ (3.7)

where $X=\left(x_1\mathrm{,}{x}_2\mathrm{,}{x}_3\right)\mathrm{,}{X}^{\prime }=\left({x^{\prime }}_1\mathrm{,}{x^{\prime }}_2\mathrm{,}{x^{\prime }}_3\right)\mathrm{,}U={\gamma }_u\left(u_1\mathrm{,}{u}_2\mathrm{,}{u}_3\right)$ .

Proof: For $t\mathrm{,}{x}_1\mathrm{,}{x}_2\mathrm{,}{x}_3$ on the hyperboloid $x_1^2+x_2^2+x_3^2-{\left(ct\right)}^2=-c^2,t>0$ , we have:

$ct=\sqrt{c^2+x_1^2+x_2^2+x_3^2}=c\sqrt{1+\frac{{\left|X\right|}^2}{c^2}}\mathrm{.}$

And by (3.1), it follows that:

$\begin{array}{c}=-\sqrt{1+\frac{{\left|X\right|}^2}{c^2}}{U}^{\text{T}}+X^{\text{T}}+\frac{{\gamma }_u-1}{{\left|u\right|}^2}{u}^{\text{T}}u{X}^{\text{T}}\\ =-\sqrt{1+\frac{{\left|X\right|}^2}{c^2}}{U}^{\text{T}}+X^{\text{T}}+\frac{{\gamma }_u-1}{{\left|u\right|}^2}\left(u\cdot X\right)u^{\text{T}}\\ =X^{\text{T}}+\left(-\sqrt{1+\frac{{\left|X\right|}^2}{c^2}}+\frac{\frac{1}{c^2}U\cdot X}{\sqrt{1+\frac{{\left|U\right|}^2}{c^2}}+1}\right)U^{\text{T}}\mathrm{.}\end{array}$

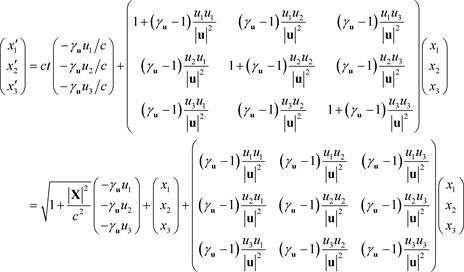
n

Remark 3.1. Lorentz transformations are essentially different from rotations in 4-dimensional Euclidean space, since by Theorem 3.1 Lorentz transformations can reduce to 3-dimension but rotations can’t.

Theorem 3.2. A Lorentz boost is the composition of an inversion with a reflection. More precisely, $X^{\prime }=L_U\left(X\right)=T_U^{vp}\left(X\right)=r_U\circ i_U^{vp}\left(X\right)$ .

Proof: Comparing Formulas (6) and (7), we have $L_U\left(X\right)=T_U^{vp}\left(X\right)$ .n

Remark 3.2. By Theorem 3.2, Remark 2.4 and Definition 2.1 of addition in hyperbolic space, Lorentz boost is a translation operation of hyperbolic space.

By Theorem 2.1 and Theorem 3.2, we get the geometric meaning of Lorentz boosts.

Theorem 3.3 (Geometric meaning of Lorentz boosts). The Lorentz boost $L_U\left(X\right)=T_U^{vp}\left(X\right)$ of $X\in \left\{x\in {ℝ}^3\mathrm{<mo>\; |\; </mo>}\sqrt{1+\frac{{\left|x\right|}^2}{c^2}}-\frac{\frac{1}{c^2}U\cdot x}{\sqrt{1+\frac{{\left|U\right|}^2}{c^2}}-1}<0\right\}$ can be drawn as follows (Figure 3): Make a sphere S with center $0$ and radius $\left|\stackrel{\leftarrow }{0X}\right|$ , whose intersection with hyperboloid $H_U$ is a circle, and the hyperplane on which the intersection circle lies is denoted as $\Pi$ . Through $X$ , we draw a line that is parallel to the vector $\stackrel{\leftarrow }{0U}$ . This line intersects the hyperplane $\Pi$ at $B$ . Extend the vector $\stackrel{\leftarrow }{XB}$ by $\sqrt{1+\frac{{\left|U\right|}^2}{c^2}}+1$ times, we get a vector $\stackrel{\leftarrow }{XC}$ , then $C=i_U^{vp}\left(X\right)$ . Furthermore, the symmetric point of $C$ with respect to the vector subspace perpendicular to $\stackrel{\leftarrow }{0U}$ is $L_U\left(X\right)$ .

Theorem 3.4. A proper orthochronous Lorentz transformation is the composition of a Euclidian rotation with an inversion and a reflection.

Proof: First, a proper orthochronous Lorentz transformation is the composition of a Lorentz boost and a Euclidian rotation [4] . Furthermore, by Theorem 3.2, a Lorentz boost is the composition of an inversion with a reflection.n

Remark 3.3. By Theorem 3.4, the geometric meaning of proper orthochronous Lorentz transformations is clear.

4. Geometric Meaning of Relativistic Addition of Velocities

Consider the worldline of a particle in uniform motion which has velocity $v=\left(v_1\mathrm{,}{v}_2\mathrm{,}{v}_3\right)$ in inertial coordinate system S. Along the particle worldline, the inertial coordinates $t\mathrm{,}x\mathrm{,}y\mathrm{,}z$ are functions of the proper time $\tau$ . The four-velocity of the particle is:

$V=\left(V_0\mathrm{,}{V}_1\mathrm{,}{V}_2\mathrm{,}{V}_3\right)\mathrm{<mo>\; :\; </mo>}=\left(c\frac{\text{d}t}{\text{d}\tau }\mathrm{,}\frac{\text{d}x}{\text{d}\tau }\mathrm{,}\frac{\text{d}y}{\text{d}\tau }\mathrm{,}\frac{\text{d}z}{\text{d}\tau }\right).$ (4.1)

The proper velocity of the particle is:

$V\mathrm{<mo>\; :\; </mo>}=\left(V_1\mathrm{,}{V}_2\mathrm{,}{V}_3\right)=\left(\frac{\text{d}x}{\text{d}\tau }\mathrm{,}\frac{\text{d}y}{\text{d}\tau }\mathrm{,}\frac{\text{d}z}{\text{d}\tau }\right)\mathrm{.}$ (4.2)

The relativity admissible velocity of the particle is:

$v=\left(v_1\mathrm{,}{v}_2\mathrm{,}{v}_3\right)=\left(\frac{\text{d}x}{\text{d}t}\mathrm{,}\frac{\text{d}y}{\text{d}t}\mathrm{,}\frac{\text{d}z}{\text{d}t}\right)\mathrm{.}$ (4.3)

Since

$\frac{\text{d}t}{\text{d}\tau }={\gamma }_v=\frac{1}{\sqrt{1-\frac{{\left|v\right|}^2}{c^2}}}\mathrm{,}$ (4.4)

it follows that:

$\left(V_0\mathrm{,}{V}_1\mathrm{,}{V}_2\mathrm{,}{V}_3\right)={\gamma }_v\left(c\mathrm{,}v\right)\mathrm{,}-V_0^2+V_1^2+V_2^2+V_3^2=-c^2\mathrm{,}$ (4.5)

and

${\gamma }_v=\frac{V_0}{c}=\sqrt{1+\frac{V_1^2+V_2^2+V_3^2}{c^2}}=\mathrm{<mo>\; :\; </mo>}{\beta }_V\mathrm{.}$ (4.6)

Remark 4.1. The relations of these three kind of velocities are $V={\phi }_{13}\left(v\right)$ , $V={\phi }_{14}\left(V\right)$ . In view of (4.5), the space of four-velocities, endowed with metric $\text{d}{s}^2={-\text{d}{V}_0^2+\text{d}{V}_1^2+\text{d}{V}_2^2+\text{d}{V}_3^2|}_{H_{+}^3\left(c\right)}$ , is just hyperboloid model ${ℍ}_h^3\left(c\right)$ . The space of relativity admissible velocities, endowed with metric ${\phi }_{13}^{\mathrm{<mo>\; *\; </mo>}}\left(\text{d}{s}^2\right)$ , is projective model ${ℍ}_p^3\left(c\right)$ . The space of proper velocities, endowed with metric ${\phi }_{14}^{\mathrm{<mo>\; *\; </mo>}}\left(\text{d}{s}^2\right)$ , is VP model ${ℍ}_{vp}^3\left(c\right)$ .

Let $\left({V^{\prime }}_0\mathrm{,}{V^{\prime }}_1\mathrm{,}{V^{\prime }}_2\mathrm{,}{V^{\prime }}_3\right)$ be the four-velocity of the particle with respect to the system S'. Then take the derivative with respect to proper time $\tau$ in Equation (3.1), we have:

$\left(\begin{array}{c}{V^{\prime }}_0\\ {V^{\prime }}_1\\ {V^{\prime }}_2\\ {V^{\prime }}_3\end{array}\right)=\left(\begin{array}{cccc}{\gamma }_u& -{\gamma }_u{u}_1/c& -{\gamma }_u{u}_2/c& -{\gamma }_u{u}_3/c\\ -{\gamma }_u{u}_1/c& 1+\left({\gamma }_u-1\right)\frac{u_1{u}_1}{{\left|u\right|}^2}& \left({\gamma }_u-1\right)\frac{u_1{u}_2}{{\left|u\right|}^2}& \left({\gamma }_u-1\right)\frac{u_1{u}_3}{{\left|u\right|}^2}\\ -{\gamma }_u{u}_2/c& \left({\gamma }_u-1\right)\frac{u_2{u}_1}{{\left|u\right|}^2}& 1+\left({\gamma }_u-1\right)\frac{u_2{u}_2}{{\left|u\right|}^2}& \left({\gamma }_u-1\right)\frac{u_2{u}_3}{{\left|u\right|}^2}\\ -{\gamma }_u{u}_3/c& \left({\gamma }_u-1\right)\frac{u_3{u}_1}{{\left|u\right|}^2}& \left({\gamma }_u-1\right)\frac{u_3{u}_2}{{\left|u\right|}^2}& 1+\left({\gamma }_u-1\right)\frac{u_3{u}_3}{{\left|u\right|}^2}\end{array}\right)\left(\begin{array}{c}{V}_0\\ V_1\\ V_2\\ V_3\end{array}\right)$ (4.7)

$=\left(\begin{array}{cccc}{U}_0/c& -U_1/c& -U_2/c& -U_3/c\\ -U_1/c& 1+\left(\frac{U_0}{c}-1\right)\frac{U_1{U}_1}{{\left|U\right|}^2}& \left(\frac{U_0}{c}-1\right)\frac{U_1{U}_2}{{\left|U\right|}^2}& \left(\frac{U_0}{c}-1\right)\frac{U_1{U}_3}{{\left|U\right|}^2}\\ -U_2/c& \left(\frac{U_0}{c}-1\right)\frac{U_2{U}_1}{{\left|U\right|}^2}& 1+\left(\frac{U_0}{c}-1\right)\frac{U_2{U}_2}{{\left|U\right|}^2}& \left(\frac{U_0}{c}-1\right)\frac{U_2{U}_3}{{\left|U\right|}^2}\\ -U_3/c& \left(\frac{U_0}{c}-1\right)\frac{U_3{U}_1}{{\left|U\right|}^2}& \left(\frac{U_0}{c}-1\right)\frac{U_3{U}_2}{{\left|U\right|}^2}& 1+\left(\frac{U_0}{c}-1\right)\frac{U_3{U}_3}{{\left|U\right|}^2}\end{array}\right)\left(\begin{array}{c}{V}_0\\ V_1\\ V_2\\ V_3\end{array}\right)$ (4.8)

$={\left(\frac{U_0{V}_0-U\cdot V}{c}\mathrm{,}-\frac{V_0}{c}U+V+\left(\frac{U_0}{c}-1\right)\frac{U\cdot V}{{\left|U\right|}^2}U\right)}^{\text{T}}$ (4.9)

which, comparing with the non-relativistic case, may be heuristically understood as the relativistic “composition velocity” of four-velocities $-U\mathrm{<mo>\; :\; </mo>}=\left(U_0\mathrm{,}-U_1\mathrm{,}-U_2\mathrm{,}-U_3\right)$ (the physical reverse 4-velocity of 4-velocity $U=\left(U_0\mathrm{,}{U}_1\mathrm{,}{U}_2\mathrm{,}{U}_3\right)$ ) and V. Notice Formula (2.12), it is recognized as the addition in hyperboloid model ${ℍ}_h^3\left(c\right)$ :

$V^{\prime }=\left(-U\right){\#}_{h}V\mathrm{.}$ (4.10)

Thus, the space of four-velocities forms hyperboloid model ${ℍ}_h^3\left(c\right)$ and the relativistic addition of four-velocities is exactly the addition in ${ℍ}_h^3\left(c\right)$ as defined in Section 2 Definition 2.1.

Since $V={\phi }_{13}\left(v\right)$ , the relativistic addition of relativity admissible velocities $u$ and $v$ is given by:

$\begin{array}{c}u{\#}_{p}v={\phi }_{13}^{-1}\left({\phi }_{13}\left(u\right){\#}_h{\phi }_{13}\left(v\right)\right)\\ =\frac{1}{1+\frac{u\cdot v}{c^2}}\left\{u+\frac{1}{{\gamma }_u}v+\frac{1}{c^2}\frac{{\gamma }_u}{1+{\gamma }_u}\left(u\cdot v\right)u\right\}\\ =\frac{1}{1+\frac{u\cdot v}{c^2}}\left\{u+v+\frac{1}{c^2}\frac{{\gamma }_u}{1+{\gamma }_u}u\times \left(u\times v\right)\right\}\mathrm{,}\end{array}$ (4.11)

which is the well-known Einstein velocity addition formula. By Proposition 2.2, the space of relativity admissible velocities forms projective model ${ℍ}_p^3\left(c\right)$ and the relativistic addition of relativity admissible velocities is exactly the addition in ${ℍ}_p^3\left(c\right)$ as defined in Definition 2.1.

Since $V={\phi }_{14}\left(V\right)$ , the relativistic addition of proper velocities $U$ and $V$ is given by:

$\begin{array}{l}U{\#}_{vp}V={\phi }_{14}^{-1}\left({\phi }_{14}\left(U\right){\#}_h{\phi }_{14}\left(V\right)\right)\\ =U+V+\left\{\frac{1}{\sqrt{1+\frac{{\left|U\right|}^2}{c^2}}+1}\frac{U\cdot V}{c^2}+\sqrt{1+\frac{{\left|V\right|}^2}{c^2}}-1\right\}U\\ =T_{-U}^{vp}\left(V\right)\left(\text{by}\left(\text{2}.\text{6}\right)\right).\end{array}$ (4.12)

In view of Proposition 2.2, the space of proper velocities forms VP model ${ℍ}_{vp}^3\left(c\right)$ and the relativistic addition of proper velocities is exactly the addition in ${ℍ}_{vp}^3\left(c\right)$ as defined in Definition 2.1.

Remark 4.2. Comparing (3.7) and (4.12), it is interesting to notice that in VP model ${ℍ}_{vp}^3\left(c\right)$ Lorentz transformation and velocity addition are given by the same formula, so they are equivalent to each other.

Proposition 4.1.

${\beta }_{U{\#}_{vp}V}={\beta }_U{\beta }_V+\frac{U\cdot V}{c^2}\mathrm{,}$ (4.13)

$\left|U{\#}_{vp}V\right|=\left|V{\#}_{vp}U\right|=c\sqrt{{\left({\beta }_U{\beta }_V+\frac{U\cdot V}{c^2}\right)}^2-1}\mathrm{.}$ (4.14)

By Formula (4.12) and Theorem 2.1, we get the geometric meaning of relativistic addition formula of velocities.

Theorem 4.1 (Geometric meaning of relativistic velocity addition). The relativistic velocity addition $U{\#}_{vp}V=T_{-U}^{vp}\left(V\right)$ of $V\in \left\{x\in {ℝ}^3\mathrm{<mo>\; |\; </mo>}\sqrt{1+\frac{{\left|x\right|}^2}{c^2}}+\frac{\frac{1}{c^2}U\cdot x}{\sqrt{1+\frac{{\left|U\right|}^2}{c^2}}-1}<0\right\}$ can be drawn as follows (Figure 4): Make a sphere S with center $0$ and radius $\left|\stackrel{\leftarrow }{0V}\right|$ , whose intersection with hyperboloid $H_{-U}$ is a circle, and the hyperplane on which the intersection circle lies is denoted as $\Pi$ . Through $V$ , we draw a line that is parallel to the vector $\stackrel{\leftarrow }{0U}$ . This line intersects the hyperplane $\Pi$ at $B$ . Extend the vector $\stackrel{\leftarrow }{VB}$ by $\sqrt{1+\frac{{\left|U\right|}^2}{c^2}}+1$ times, we get a vector $\stackrel{\leftarrow }{VC}$ , then $C=i_{-U}^{vp}\left(V\right)$ . Furthermore, the symmetric point of $C$ with respect to the vector subspace perpendicular to $\stackrel{\leftarrow }{0U}$ is $U{\#}_{vp}V$ .

Proof: By Formulas (2.6) and (4.12), we have:

$U{\#}_{vp}V=T_{-U}^{vp}\left(V\right)=r_{-U}\circ i_{-U}^{vp}\left(V\right)=r_U\circ i_{-U}^{vp}\left(V\right)\mathrm{.}$ (4.15)

n

Remark 4.3. The dilation factor in Theorem 4.1 is the gamma factor plus one, i.e. $\sqrt{1+\frac{{\left|U\right|}^2}{c^2}}+1={\beta }_U+1$ .

Remark 4.4. When $c\to \infty$ , Lorentz transformation turns into Galilean transformation and addition in hyperbolic space reduces to ordinary addition in Euclidean space.

5. Successive Lorentz Transformations and Thomas Precession

Consider composition of Lorentz boots given by (3.2), by polar decomposition, we have [4] :

$B\left(u\right)B\left(v\right)=B\left(u{\#}_{p}v\right)R\left(\Omega \left[u\mathrm{,}v\right]\right)\mathrm{,}$ (5.1)

where

$R\left(\Omega \left[u\mathrm{,}v\right]\right)=\left(\begin{array}{cc}1& 0\\ 0^{\text{T}}& \Omega \left[u\mathrm{,}v\right]\end{array}\right)\mathrm{,}$ (5.2)

where $\Omega \left[u\mathrm{,}v\right]$ is an unimodular orthogonal matrix, called Thomas rotation, and is given by:

$\Omega \left[u\mathrm{,}v\right]=M-\frac{b^{\text{T}}a}{1+\gamma }\mathrm{,}$ (5.3)

and where:

$\gamma ={\gamma }_u{\gamma }_v\left(1+\frac{u\cdot v}{c^2}\right)\mathrm{,}$ (5.4)

$a={\gamma }_u{\gamma }_v\frac{v}{c}+{\gamma }_u\frac{u}{c}+{\gamma }_u\left({\gamma }_v-1\right)\frac{\left(u\cdot v\right)v}{c{\left|v\right|}^2}\mathrm{,}$ (5.5)

$b={\gamma }_u{\gamma }_v\frac{u}{c}+{\gamma }_v\frac{v}{c}+{\gamma }_v\left({\gamma }_u-1\right)\frac{\left(u\cdot v\right)u}{c{\left|u\right|}^2}\mathrm{,}$ (5.6)

$M=1_3+{\gamma }_u-1\frac{u^{\text{T}}u}{\left|u\right|}+\left({\gamma }_v-1\right)\frac{v^{\text{T}}v}{{\left|v\right|}^2}+\left[{\gamma }_u{\gamma }_v\frac{\left|u\right|\left|v\right|}{c^2}+\left({\gamma }_u-1\right)\left({\gamma }_v-1\right)\frac{u\cdot v}{\left|u\right|\left|v\right|}\right]\frac{u^{\text{T}}v}{\left|u\right|\left|v\right|}\mathrm{.}$ (5.7)

The Thomas rotation takes place in the plane $span\left\{u\mathrm{,}v\right\}$ . The sense of the Thomas rotation in the $uv$ -plane is negative (we orient this plane in the usual way, such that $u\times v$ defines the direction of the normal). And the cosine of the angle of rotation $\theta$ is:

$\cos \theta =\frac{{\left(1+{\gamma }_u+{\gamma }_v+\gamma \right)}^2}{\left({\gamma }_u+1\right)\left({\gamma }_v+1\right)\left(\gamma +1\right)}-1.$ (5.8)

We have:

$u{\#}_{p}v=\Omega \left[u\mathrm{,}v\right]\left(v{\#}_{p}u\right)\mathrm{,}$ (5.9)

and for $x\in {ℝ}^3$ ,

$\begin{array}{l}\Omega \left[u\mathrm{,}v\right]x\\ =x+\left[\left({\gamma }_u-1\right)\left(1-{\gamma }_v\right)\frac{u}{\left|u\right|}+\left(2\left({\gamma }_u-1\right)\left({\gamma }_v-1\right)\frac{u\cdot v}{\left|u\right|\left|v\right|}+{\gamma }_u{\gamma }_v\frac{\left|u\right|\left|v\right|}{c^2}\right)\frac{v}{\left|v\right|}\right]\\ \cdot \frac{x}{1+\gamma }\frac{u^{\text{T}}}{\left|u\right|}+\left[-{\gamma }_u{\gamma }_v\frac{\left|v\right|}{c}\frac{u}{c}+\left({\gamma }_u-1\right)\left(1-{\gamma }_v\right)\frac{v}{\left|v\right|}\right]\cdot \frac{x}{1+\gamma }\frac{v^{\text{T}}}{\left|v\right|}\\ \mathrm{<mo>\; =\; </mo>}x+\left[\frac{{\gamma }_u^2\left(1-{\gamma }_v\right)}{c^2\left(1+{\gamma }_u\right)}u\cdot x+\left(\frac{{\gamma }_u{\gamma }_v}{c^2}+\frac{2{\gamma }_u^2{\gamma }_v^2\left(u\cdot v\right)}{c^4\left({\gamma }_u+1\right)\left({\gamma }_v+1\right)}\right)v\cdot x\right]\frac{u^{\text{T}}}{1+\gamma }\\ +\left[\frac{{\gamma }_v^2\left(1-{\gamma }_u\right)}{c^2\left(1+{\gamma }_v\right)}v\cdot x-\frac{{\gamma }_u{\gamma }_v}{c^2}u\cdot x\right]\frac{v^{\text{T}}}{1+\gamma }\mathrm{.}\end{array}$ (5.10)

The corresponding results in VP model are as follows:

$\begin{array}{l}\Omega \left[U\mathrm{,}V\right]X\\ =X+\left[\frac{1-{\beta }_V}{c^2\left(1+{\beta }_U\right)}U\cdot X+\left(\frac{1}{c^2}+\frac{2\left(U\cdot V\right)}{c^4\left({\beta }_U+1\right)\left({\beta }_V+1\right)}\right)V\cdot X\right]\frac{U^T}{1+{\beta }_{U{\#}_{vp}V}}\\ +\left[\frac{1-{\beta }_U}{c^2\left(1+{\beta }_V\right)}V\cdot X-\frac{1}{c^2}U\cdot X\right]\frac{V^{\text{T}}}{1+{\beta }_{U{\#}_{vp}V}}\mathrm{,}\end{array}$ (5.11)

$L_U\circ L_V\left(X\right)=L_{U{\#}_{vp}V}\left(\Omega \left[U\mathrm{,}V\right]X\right)\mathrm{,}$ (5.12)

$U{\#}_{vp}V=\Omega \left[U\mathrm{,}V\right]\left(V{\#}_{vp}U\right)\mathrm{,}$ (5.13)

$\cos \theta =\frac{{\left(1+{\beta }_U+{\beta }_V+{\beta }_{U{\#}_{vp}V}\right)}^2}{\left({\beta }_U+1\right)\left({\beta }_V+1\right)\left({\beta }_{U{\#}_{vp}V}+1\right)}-1.$ (5.14)

Corollary 5.1 (Geometric meaning of $U{\#}_{vp}V$ for fixed $V$ ). First, repeat the procedure of Theorem 4.1, we get $U{\#}_{vp}V$ , then rotate an angle $\theta$ , which is given by (5.14), in the $UV$ -plane in the negative direction yields $U{\#}_{vp}V$ .

6. Conclusion

In conclusion, Lorentz transformation and relativistic addition of velocities in VP model ${ℍ}_{vp}^3\left(c\right)$ have fairly intuitive descriptions. Since the hyperboloid model ${ℍ}_h^3\left(c\right)$ is the same as the VP model ${ℍ}_{vp}^3\left(c\right)$ up to a vertical projection, the geometric meaning of Lorentz transformation and relativistic addition of velocities in ${ℍ}_h^3\left(c\right)$ are also clear now.