Abstract

In this paper, we consider the following noncooperative elliptic systems where Ω is a bounded domain in R^N with smooth boundary ∂Ω, λ,δ,γ are real parameters, and . We assume that F is subquadratic at zero with respect to the variables u,v. By using a variant Clark’s theorem, we obtain infinitely many nontrivial solutions (u_k,v_k) with as k → ∞. Compared with the existing literature, we do not need to assume the behavior of the nonlinearity ∇F at infinity.

Keywords

Noncooperative Elliptic Systems, (PS)^* Condition, Clark’s Theorem

Share and Cite:

1. Introduction

In this paper, we consider the existence of nontrivial solutions for the following variational noncooperative elliptic system

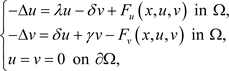
where $\Omega$ is a bounded smooth domain in $R^N$ with smooth boundary $\partial \Omega$ , the numbers $\lambda ,\delta ,\gamma$ are real parameters, and $F\in C^1\left(\bar{\Omega }\times {ℝ}^2,ℝ\right)$ such that $\nabla F=\left(F_u,F_v\right)$ . Here $\nabla F$ denotes the gradient of F in the variables u and v.

System (P) is the so-called noncooperative elliptic system, arising naturally a steady state in reaction-diffusion process that appears in chemical and biological phenomena, including the steady and unsteady state situation (see [1] [2] [3] [4] and references therein). System (P) has been extensively studied in last three decades by using the variational methods under various conditions (see [1] - [17] ). In [1] , Costa and Magalhães established the variational structure to the noncooperative elliptic systems and obtained several existence results under the non-quadraticity at infinity by using minimax methods. In [5] , by using a variant fountain theorem, Bartsch and Figueiredo obtained infinitely many nontrivial solutions for nonlinear noncooperative elliptic systems when $F\left(x,u,v\right)$ satisfied the non-quadraticity condition at infinity. In [6] , Guo obtained the existence and multiplicity of nontrivial solutions for resonant noncooperative elliptic systems by using a new version of Morse theory for strongly indefinite functionals. In [7] , Ke and Tang established the existence of a nontrivial solution for a class of noncooperative elliptic systems with nonlinearities of sup-linear growth by using the minimax methods. In [17] , Zou obtained the multiplicity of nontrivial solutions with the number of them that depends on the dimension of the eigenspaces between resonant values when the noncooperative system is resonant both at zero and at infinity by using a new abstract critical point theorem.

In this paper, we shall study the system (P) when $F\left(x,u,v\right)$ is subquadratic at zero. Compared with the existing results, we do not need to make any assumptions at infinity on the nonlinearity. The nonlinearity can be subquadratic, asymptotically quadratic or superquadratic at infinity. Under this general condition, we shall prove that system (P) has infinitely many nontrivial solutions $\left(u_k,v_k\right)$ with ${\Vert \left(u_k,v_k\right)\Vert }_{L^{\infty }}\to 0$ as $k\to \infty$ . Our main tool is a variant of the Clark’s theorem established by Liu and Wang [18] . In [18] , the authors extended the classical Clark’s theorem and gave a variant of the Clark’s theorem for the strongly indefinite functionals, then they used it to study the sublinear Hamiltonian systems and obtained infinitely many periodic solutions. We make the following assumptions:

(F₁) $F\in C^1\left(\bar{\Omega }\times {ℝ}^2,ℝ\right)$ , and $F\left(x,0,0\right)=0$ ,

(F₂) there exists a $\delta >0$ such that $F\left(x,-u,-v\right)=F\left(x,u,v\right)$ , $\forall x\in \bar{\Omega }$ , $\forall \left(u,v\right)\in B_{\delta }$ , where $B_{\delta }:=\left\{\left(u,v\right)\in {ℝ}^2|\left|\left(u,v\right)\right|=\sqrt{u^2+v^2}<\delta \right\}$ ,

(F₃) $\underset{\left|\left(u,v\right)\right|\to 0}{\lim }\frac{F\left(x,u,v\right)}{{\left|\left(u,v\right)\right|}^2}=+\infty$ uniformly in $x\in \bar{\Omega }$ .

Now we state our main result.

Theorem 1.1. Assume that (F₁)-(F₃) hold, then the system (P) has infinitely many solutions $\left(u_k,v_k\right)$ such that ${\Vert \left(u_k,v_k\right)\Vert }_{L^{\infty }}\to 0$ as $k\to \infty$ .

Remark 1.2. Now we give a comparison between our result and some existing results. In the previous works, the authors always need to make the assumptions on the nonlinearity at infinity. For example, the sub-quadratic cases were considered in [1] , the superquadratic cases were considered in [2] [4] [7] [8] [12] [14] and the asymptotically quadratic cases were considered in [6] [9] [11] [13] [15] [16] [17] . Compared with these results, our nonlinearity F is general at infinity, we do not need to assume the behavior of the nonlinear term F at infinity. Besides, instead of the global symmetry condition: $F\left(x,-u,-v\right)=F\left(x,u,v\right)$ , $\forall \left(x,u,v\right)\in \bar{\Omega }\times {ℝ}^2$ , we only need the local symmetry condition (F₂).

Example 1.3. Let $a\left(x\right)$ be a continuously differentiable positive function on $\bar{\Omega }$ . Let

$F_1\left(x,u,v\right)=a\left(x\right){\left(u^2+v^2\right)}^{\frac{\sigma }{2}}$ ,

$F_2\left(x,u,v\right)=a\left(x\right)\left[{\left(u^2+v^2\right)}^{\frac{\sigma }{2}}+\left(u^2+v^2\right)\right],$

$F_3\left(x,u,v\right)=a\left(x\right)\left[{\left(u^2+v^2\right)}^{\frac{\sigma }{2}}+{\left(u^2+v^2\right)}^{\frac{\theta }{2}}\right],$

where $1<\sigma <2$ , $\theta >2$ . It is not difficult to see that $F_1,F_2$ and $F_3$ are all satisfies the conditions (F₁)-(F₃), but they are subquadratic, asymptotically quadratic and superquadratic at infinity respectively.

Now we give a detailed explanation of our proof. Firstly, we modify the nonlinearity. We choose a modified function $\tilde{F}$ and consider the corresponding modified elliptic system. We define the functional corresponding to this modified system. And due to the resonance of the modified system, we use a penalized functional technique and construct a penalized functional. Secondly, we show that the penalized functional satisfies the ${\left(PS\right)}^{\ast }$ condition and is bounded from below, and prove that the penalized functional satisfies the other conditions of the Clark’s theorem. Finally, by using the Clark’s theorem we prove that the penalized functional has a sequence of nontrivial critical points $\left\{\left(u_k,v_k\right)\right\}$ with their $L^{\infty }$ norm tending to zero. By using this fact, we conclude that they are nontrivial solutions of the system (P) for k large enough.

The paper is organized as follows. In Section 2, we give some preliminary results about the variational structure of the system (P) and a new abstract critical point theorem for the indefinite functional. In Section 3, we give the proof of our main result.

2. Preliminaries

In this section, we give the preliminary results and a variant of Clark’s theorem to prove the Theorem 1.1.

Let $H_0^1\left(\Omega \right)$ be the usual Sobolev space with the inner product

$\langle u,v\rangle ={\displaystyle {\int }_{\Omega }\nabla u\cdot \nabla v\text{d}x},\forall u,v\in H_0^1\left(\Omega \right),$

and the corresponding norm $\Vert \cdot \Vert$ . Denote $U=\left(u,v\right)$ and set $E:=H_0^1\left(\Omega \right)\times H_0^1\left(\Omega \right)$ . The inner product and norm of E are given by

$\langle U,\Phi \rangle =\langle u,\phi \rangle +\langle v,\psi \rangle ,{\Vert U\Vert }^2={\Vert u\Vert }^2+{\Vert v\Vert }^2,$

where $U=\left(u,v\right)$ and $\Phi =\left(\phi ,\psi \right)$ are in E. We use ${\Vert \cdot \Vert }_{L^p}$ to denote the norm of $L^p:=L^p\left(\Omega \right)\times L^p\left(\Omega \right)$ for $1\le p\le \infty$ .

For simplicity, we suppose that $\lambda \ge \gamma$ and $\delta >0$ . Let

$A=\left(\begin{array}{cc}\lambda & -\delta \\ \delta & \gamma \end{array}\right),R=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),U=\left(u,v\right),-\stackrel{\to }{\Delta }U=\left(\begin{array}{c}-\Delta u\\ -\Delta v\end{array}\right).$

Denote by $\sigma \left(A\right)=\left\{\zeta ,\eta \right\}$ the eigenvalues of A and $\sigma \left(-\Delta \right)=\left\{{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_j,\cdots \right\}$ for the eigenvalues of $-\Delta$ on $H_0^1\left(\Omega \right)$ .

Define the operator $\mathcal{L}$ by $\mathcal{L}U=-R\stackrel{\to }{\Delta }U-RAU$ , $U\in E$ . Then, the eigenvalues of the linear problem $\mathcal{L}U=kU$ have the form (see [2] )

${\Lambda }_j^{\pm }=-\frac{\lambda -\gamma }{2}\pm \sqrt{{\left(\frac{\lambda -\gamma }{2}\right)}^2+\det \left({\lambda }_j-A\right)}.$ (2.1)

We only consider the case of $0\in \sigma \left(\mathcal{L}\right)$ , the case of $0\notin \sigma \left(\mathcal{L}\right)$ is similar and simpler. Then let

$\sigma \left(\mathcal{L}\right)=\left\{\cdots <{\mu }_{-2}<{\mu }_{-1}<0={\mu }_0<{\mu }_1<{\mu }_2<\cdots \right\}$

denote all the eigenvalues of the eigenvalue problem $\mathcal{L}U=kU$ . And denote by $E\left({\mu }_i\right)$ the eigenspace corresponding to ${\mu }_i,i\in \mathbb{Z}$ . Define the operator L on E by

$\langle LU,\Phi \rangle ={\langle \mathcal{L}U,\Phi \rangle }_{L^2}={\displaystyle {\int }_{\Omega }\left(-R\stackrel{\to }{\Delta }U-RAU\right)}\cdot \Phi \text{d}x,\forall U,\Phi \in E.$

Then L is a bounded self-adjoint linear operator on E. According to L, we can split E as $E=E^{-}\oplus E^0\oplus E^{+}$ , where $E^{+},E^{-},E^0$ are the subspaces of E on which L is positive definite, negative definite, and null. It is not difficult to see that

$E^{+}=\underset{i=1}{\overset{\infty }{\oplus }}E\left({\mu }_i\right),E^{-}=\underset{i=-\infty }{\overset{-1}{\oplus }}E\left({\mu }_i\right),E^0=E\left({\mu }_0\right).$

And there exists a constant $c>0$ , such that for any $U^{+}\in E^{+}$ , $U^{-}\in E^{-}$ ,

$\langle L{U}^{+},U^{+}\rangle \ge c{\Vert U^{+}\Vert }^2,\langle L{U}^{-},U^{-}\rangle \le -c{\Vert U^{-}\Vert }^2.$ (2.2)

In what follows, for $U\in E$ , we always write $U=U^{+}+U^0+U^{-}$ with $U^{+}\in E^{+}$ , $U^0\in E^0$ and $U^{-}\in E^{-}$ .

Choose $\tilde{F}\in C^1\left(\bar{\Omega }\times {ℝ}^2,ℝ\right)$ such that $\tilde{F}$ is even in U, $\tilde{F}\left(x,U\right)=F\left(x,U\right)$ for $\left(x,U\right)\in \bar{\Omega }\times B_{\delta }$ , and $\tilde{F}\left(x,U\right)=0$ for $\left(x,U\right)\in \bar{\Omega }\times \left({ℝ}^2\backslash B_{2\delta }\right)$ , where $B_{\delta }=\left\{U\in {ℝ}^2|\left|U\right|\le \delta \right\}$ . Consider the following elliptic system

Define the functional J on E by

$J\left(U\right)=\frac{1}{2}\langle LU,U\rangle -{\displaystyle {\int }_{\Omega }\tilde{F}\left(x,U\right)\text{d}x.}$ (2.3)

By the definition of $\tilde{F}$ , it is known that $J\in C^1\left(E,ℝ\right)$ and the solutions of (P') correspond to the critical points of J. Since $\dim E^0>0$ , the functional J may not satisfy the compact condition. To overcome this difficulty, we use a penalized functional technique. Define

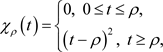
and

$J_{\rho }\left(U\right)=J\left(U\right)+{\chi }_{\rho }\left({\Vert U^0\Vert }^2\right).$ (2.4)

Then $J_{\rho }\left(U\right)\in C^1\left(E,ℝ\right)$ and $J_{\rho }\left(U\right)=J\left(U\right)$ when $U=U^{+}+U^0+U^{-}$ satisfies ${\Vert U^0\Vert }^2\le \rho$ .

In order to prove Theorem 1.1, we introduce a variant of the Clark’s theorem established by Liu and Wang [18] . Let X be a Banach space, ${\left\{X_n\right\}}_{n=0}^{\infty }$ be a sequence of infinitely dimensional closed subspaces of X such that $X_0\subset X_1\subset X_2\subset \cdots$ , the codimension $d_n$ of $X_0$ in $X_n$ is finite, and $X=\stackrel{¯}{{\displaystyle \underset{n=0}{\overset{\infty }{\cup }}{X}_n}}$ . We say that $\Phi \in C^1\left(X,ℝ\right)$ satisfies the ${\left(PS\right)}^{\ast }$ condition with respect to ${\left\{X_n\right\}}_{n=0}^{\infty }$ if for any subsequence $\left\{n_j\right\}$ of $\left\{n\right\}$ , any sequence $\left\{n_j\right\}$ such that $u_j\in X_{n_j}$ , $\Phi \left(u_j\right)$ is bounded, and ${\left(\Phi {|}_{X_{n_j}}\right)}^{\prime }\left(u_j\right)\to 0$ as $j\to \infty$ contains a subsequence converging to a critical point of $\Phi$ . Denote by $\Sigma$ the family of closed symmetric subsets of X which do not contain 0. For $A\in \Sigma$ , the genus $\gamma \left(A\right)$ of A is by definition the smallest integer n for which there exists an odd and continuous mapping $h:A\to {ℝ}^n\backslash \left\{0\right\}$ , $\gamma \left(A\right)=\infty$ if no such mapping exists, and $\gamma (\varnothing )=0$ .

Theorem 2.1 ( [18] ). Assume that $\Phi$ is even and satisfies the ${\left(PS\right)}^{\ast }$ condition with respect to ${\left\{X_n\right\}}_{n=0}^{\infty }$ , ${\Phi |}_{X_0}$ is bounded below and satisfies the (PS) condition, and $\Phi \left(0\right)=0$ . If there exists $n_0>0$ such that for any $k\in {\mathbb{Z}}^{+}$ , there exist ${\epsilon }_k>0$ , ${\rho }_k>0$ with ${\rho }_k\to 0$ , and a symmetric set $A_k\subset \left\{U\in X|\Vert u\Vert ={\rho }_k\right\}$ such that $\gamma \left(X_n\cap A_k\right)=d_n+k$ and ${\sup }_{X_n\cap A_k}\Phi <-{\epsilon }_k$ for all $n\ge n_0$ , then at least one of the following conclusions holds.

1) There exists a sequence of critical points $\left\{u_k\right\}$ satisfying $\Phi \left(u_k\right)<0$ for all k and $\Vert u_k\Vert \to 0$ as $k\to \infty$ .

2) There exists $r>0$ such that for any $0<a<r$ there exists a critical point u such that $\Vert u\Vert =a$ and $\Phi \left(u\right)=0$ .

Remark 2.2. From Theorem 2.1, it is clear that there exist a sequence of critical points $u_k\ne 0$ such that $\Phi \left(u_k\right)\le 0$ , $\Phi \left(u_k\right)\to 0$ and $\Vert u_k\Vert \to 0$ as $k\to \infty$ . The additional information on the norms of the critical points is very important in the proof of Theorem 1.1.

3. Proof of Theorem 1.1

In this section, we shall use Theorem 2.1 to prove Theorem 1.1.

Proof of theorem 1.1. Let

$X_n=\underset{i=-n+1}{\overset{\infty }{\oplus }}E\left({\mu }_i\right),n=0,1,2,\cdots ,$

then ${\left\{X_n\right\}}_0^{\infty }$ is a sequence of infinite dimensional closed subspaces of X, $X_0\subset X_1\subset X_2\subset \cdots$ , and $X=\overline{{\cup }_0^{\infty }{X}_n}$ . Let $P_n:X\to X_n$ be the orthogonal projector. The codimension $d_n$ of $X_0$ in $X_n$ is

$d_n=\dim \left(\underset{i=-n+1}{\overset{0}{\oplus }}E\left({\mu }_i\right)\right)={\displaystyle \underset{i=-n+1}{\overset{0}{\sum }}\dim }E\left({\mu }_i\right)={\displaystyle \underset{i=-n+1}{\overset{0}{\sum }}{l}_i},$

where $l_i=\dim E\left({\mu }_i\right)$ . By (F₁) and the definition of $J_{\rho }$ , we see that $J_{\rho }\in C^1\left(E,ℝ\right)$ , $J_{\rho }\left(0\right)=0$ and $J_{\rho }$ is an even functional. Now we prove that $J_{\rho }$ satisfies the other assumptions of Theorem 2.1 into three steps.

Step 1. We prove that the functional $J_{\rho }$ satisfies the ${\left(PS\right)}^{\ast }$ condition with respect to ${\left\{X_n\right\}}_0^{\infty }$ . Let $\left\{U_j\right\}\subset E$ be a ${\left(PS\right)}^{\ast }$ sequence such that

$U_j\in X_{n_j},n_j\to \infty ,J_{\rho }\left(U_j\right)\text{isbounded},\text{and}{\left(J_{\rho }{|}_{X_{n_j}}\right)}^{\prime }\left(U_j\right)\to 0\text{as}j\to \infty .$ (3.1)

By the definition of $\tilde{F}$ , there exists a constant $C>0$ such that

$\left|{\tilde{F}}_U\left(x,U\right)\right|\le C,\left|\tilde{F}\left(x,U\right)\right|\le C.$ (3.2)

Then by (2.2), (3.1), Hölder inequality and Sobolev inequality, we have

$\begin{array}{c}o\left(\Vert U_j^{+}\Vert +\Vert U_j^{-}\Vert \right)=\langle {\left({J_{\rho }|}_{X_{n_j}}\right)}^{\prime }\left(U_j\right),U_j^{+}-U_j^{-}\rangle =\langle {J^{\prime }}_{\rho }\left(U_j\right),U_j^{+}-U_j^{-}\rangle \\ =\langle L{U}_j^{+},U_j^{+}\rangle -\langle L{U}_j^{-},U_j^{-}\rangle -{\displaystyle {\int }_{\Omega }{\tilde{F}}_U\left(x,U_j\right)\cdot \left(U_j^{+}-U_j^{-}\right)\text{d}x}\\ \ge c\left({\Vert U_j^{+}\Vert }^2+{\Vert U_j^{-}\Vert }^2\right)-{\displaystyle {\int }_{\Omega }\left|{\tilde{F}}_U\left(x,U_j\right)\right|\cdot \left(\left|U_j^{+}\right|+\left|U_j^{-}\right|\right)\text{d}x}\\ \ge c\left({\Vert U_j^{+}\Vert }^2+{\Vert U_j^{-}\Vert }^2\right)-C{\displaystyle {\int }_{\Omega }\left(\left|U_j^{+}\right|+\left|U_j^{-}\right|\right)\text{d}x}\\ \ge c\left({\Vert U_j^{+}\Vert }^2+{\Vert U_j^{-}\Vert }^2\right)-C^{\prime }\left(\Vert U_j^{+}\Vert +\Vert U_j^{-}\Vert \right),\end{array}$

which implies that $\left\{U_j^{+}\right\}$ and $\left\{U_j^{-}\right\}$ are bounded in E. Next we prove that $\left\{U_j^0\right\}$ is also bounded in E. Similarly, one has

$\begin{array}{c}o\left(\Vert U_j^0\Vert \right)=\langle {\left({J_{\rho }|}_{X_{n_j}}\right)}^{\prime }\left(U_j\right),U_j^0\rangle \\ =2{{\chi }^{\prime }}_{\rho }\left({\Vert U_j^0\Vert }^2\right){\Vert U_j^0\Vert }^2-{\displaystyle {\int }_{\Omega }{\tilde{F}}_U\left(x,U_j\right)\cdot U_j^0\text{d}x}\\ \ge 2{{\chi }^{\prime }}_{\rho }\left({\Vert U_j^0\Vert }^2\right){\Vert U_j^0\Vert }^2-C{\displaystyle {\int }_{\Omega }\left|U_j^0\right|\text{d}x}\\ \ge 2{{\chi }^{\prime }}_{\rho }\left({\Vert U_j^0\Vert }^2\right){\Vert U_j^0\Vert }^2-C^{\prime }\Vert U_j^0\Vert ,\end{array}$ (3.3)

which implies that $\left\{U_j^0\right\}$ is also bounded in E by the definition of ${\chi }_{\rho }$ . Therefore $\left\{U_j\right\}$ is bounded in E. Thus there exists a $U^{*}\in E$ such that up to a subsequence,

$U_j\rightharpoonup U^{*}\text{in}E,U_j\to U^{*}\text{in}{L}^2.$ (3.4)

By (2.2), (3.1), (3.4) and note that $\left\{U_j\right\}$ is bounded in E, we have

$\begin{array}{c}0=\underset{j\to \infty }{\lim }\langle {\left({J_{\rho }|}_{X_{n_j}}\right)}^{\prime }\left(U_j\right)-{\left({J_{\rho }|}_{X_{n_j}}\right)}^{\prime }\left(U^{*}\right),U_j^{\text{+}}-U^{*\text{+}}\rangle \\ =\underset{j\to \infty }{\lim }\langle {J^{\prime }}_{\rho }\left(U_j\right)-{J^{\prime }}_{\rho }\left(U^{*}\right),U_j^{\text{+}}-P_{n_j}{U}^{*\text{+}}\rangle \\ =\underset{j\to \infty }{\lim }\langle {J^{\prime }}_{\rho }\left(U_j\right)-{J^{\prime }}_{\rho }\left(U^{*}\right),U_j^{\text{+}}-U^{*\text{+}}\rangle \\ =\underset{j\to \infty }{\lim }\langle L\left(U_j^{+}-U^{*+}\right),U_j^{+}-U^{*+}\rangle \\ -\underset{j\to \infty }{\lim }{\displaystyle {\int }_{\Omega }\left({\tilde{F}}_U\left(x,U_j\right)-{\tilde{F}}_U\left(x,U^{*}\right)\right)\cdot \left(U_j^{+}-U^{*+}\right)\text{d}x}\\ \ge c\underset{j\to \infty }{\lim }{\Vert U_j^{+}-U^{*+}\Vert }^2-\underset{j\to \infty }{\lim }{\displaystyle {\int }_{\Omega }\left({\tilde{F}}_U\left(x,U_j\right)-{\tilde{F}}_U\left(x,U^{*}\right)\right)}\cdot \left(U_j^{+}-U^{*+}\right)\text{d}x.\end{array}$ (3.5)

On the other hand, by (3.2) and (3.4)

$\begin{array}{l}\left|{\displaystyle {\int }_{\Omega }\left({\tilde{F}}_U\left(x,U_j\right)-{\tilde{F}}_U\left(x,U^{*}\right)\right)}\cdot \left(U_j^{+}-U^{*+}\right)\text{d}x\right|\\ \le 2C{\displaystyle {\int }_{\Omega }\left|U_j^{+}-U^{*+}\right|}\text{d}x\\ \le C^{\prime }{\left({\displaystyle {\int }_{\Omega }{\left|U_j^{+}-U^{*+}\right|}^2\text{d}x}\right)}^{\frac{1}{2}}\to 0\text{as}j\to \infty .\end{array}$ (3.6)

Then by (3.5) and (3.6) we have that $U^{*}\in E$ , that is $U_j^{+}\to U^{*+}$ in E. Similarly, we have $U_j^{-}\to U^{*-}$ in E. On the other hand, notice that $E^0$ is a finite dimensional space, we have $U_j^{-}\to U^{*-}$ in E. Hence we conclude that $U_j\to U^{*}$ in E and the ${\left(PS\right)}^{*}$ condition is proved.

Step 2. We prove that ${J_{\rho }|}_{X_0}$ is bounded from below and satisfies the (PS) condition. Note that $X_0=E^{+}$ , then by (2.2), for $U\in X_0$ we have

${J_{\rho }|}_{X_0}\left(U\right)=\frac{1}{2}\langle LU,U\rangle -{\displaystyle {\int }_{\Omega }\tilde{F}}\left(x,U\right)\text{d}x\ge \frac{c}{2}{\Vert U\Vert }^2-C,$ (3.7)

which implies that ${J_{\rho }|}_{X_0}$ is bounded from below. Now we prove that ${J_{\rho }|}_{X_0}$ satisfies the (PS) condition. Assume that $\left\{U_n\right\}\subset X_0$ satisfies that

${J_{\rho }|}_{X_0}\left(U_n\right)\mathrm{is}bounded,\text{and}{\left({J_{\rho }|}_{X_0}\right)}^{\prime }\left(U_n\right)\to 0.$ (3.8)

By (3.7), we see that $\left\{U_n\right\}$ is bounded in $X_0$ . Then up to a subsequence there exists a $\bar{U}\in X_0$ such that

$U_n\rightharpoonup \bar{U}\text{in}{X}_0,\text{and}{U}_n\to \bar{U}\text{in}{L}^2.$ (3.9)

Then by (2.2), (3.8), (3.9), Hölder inequality and Sobolev inequality, we have

$\begin{array}{c}o\left(1\right)=\langle {\left({J_{\rho }|}_{X_0}\right)}^{\prime }\left(U_n\right)-{\left({J_{\rho }|}_{X_0}\right)}^{\prime }\left(\bar{U}\right),U_n-\bar{U}\rangle \\ =\langle {J^{\prime }}_{\rho }\left(U_n\right)-{J^{\prime }}_{\rho }\left(\bar{U}\right),U_n-\bar{U}\rangle \\ =\langle L\left(U_n-\bar{U}\right),U_n-\bar{U}\rangle -{\displaystyle {\int }_{\Omega }\left({\tilde{F}}_U\left(x,U_n\right)-{\tilde{F}}_U\left(x,\bar{U}\right)\right)}\cdot \left(U_n-\bar{U}\right)\text{d}x\\ \ge c{\Vert U_n-\bar{U}\Vert }^2-{\displaystyle {\int }_{\Omega }\left|{\tilde{F}}_U\left(x,U_n\right)-{\tilde{F}}_U\left(x,\bar{U}\right)\right|\cdot \left|U_n-\bar{U}\right|\text{d}x}\\ \ge c{\Vert U_n-\bar{U}\Vert }^2-2C{\displaystyle {\int }_{\Omega }\left|U_n-\bar{U}\right|\text{d}x}\\ \ge c{\Vert U_n-\bar{U}\Vert }^2-C^{\prime }{\left({\displaystyle {\int }_{\Omega }{\left|U_n-\bar{U}\right|}^2}\right)}^{\frac{1}{2}}.\end{array}$ (3.10)

Then by (3.9) and (3.10), we have that $U_n\to \bar{U}$ in $X_0$ . An the (PS) condition is proved.

Step 3. We prove that there exists $n_0>0$ such that for any $k\in {\mathbb{Z}}^{+}$ , there exist ${\epsilon }_k>0$ , ${\rho }_k>0$ with ${\rho }_k\to 0$ , and a symmetric set $A_k\subset \left\{U\in X|\Vert u\Vert ={\rho }_k\right\}$ such that $\gamma \left(X_n\cap A_k\right)=d_n+k$ and ${\sup }_{X_n\cap A_k}{J}_{\rho }<-{\epsilon }_k$ for all $n\ge n_0$ .

For any $T>0$ , from (F₃) and the definition of $\tilde{F}$ , we can find $C=C\left(T\right)>0$ such that

$\tilde{F}\left(x,U\right)\ge T{\left|U\right|}^2-C\left(T\right){\left|U\right|}^4,\forall U\in {ℝ}^2.$

Note that ${\chi }_{\rho }\left(t\right)\le t^2$ , $\forall t\ge 0$ , by the definition of ${\chi }_{\rho }$ . Let $m\ge 1$ and $U\in {\oplus }_{i=-\infty }^{m}E\left({\mu }_i\right)$ , then we have

$\begin{array}{c}{J}_{\rho }\left(U\right)=\frac{1}{2}\langle L{U}^{+},U^{+}\rangle +\frac{1}{2}\langle L{U}^{-},U^{-}\rangle -{\displaystyle {\int }_{\Omega }\tilde{F}\left(x,U\right)\text{d}x}+{\chi }_{\rho }\left({\Vert U^0\Vert }^2\right)\\ \le \frac{\Vert L\Vert }{2}{\Vert U^{+}\Vert }^2-\frac{c}{2}{\Vert U^{-}\Vert }^2-T{\displaystyle {\int }_{\Omega }{\left|U\right|}^2\text{d}x}+C\left(T\right){\displaystyle {\int }_{\Omega }{\left|U\right|}^4\text{d}x}+{\chi }_{\rho }\left({\Vert U^0\Vert }^2\right)\\ \le \frac{\Vert L\Vert }{2}{\Vert U^{+}\Vert }^2-\frac{c}{2}{\Vert U^{-}\Vert }^2-T{\displaystyle {\int }_{\Omega }{\left|U^{+}\right|}^2\text{d}x}-T{\displaystyle {\int }_{\Omega }{\left|U^{-}\right|}^2\text{d}x}\\ -T{\displaystyle {\int }_{\Omega }{\left|U^0\right|}^2\text{d}x}+C\left(T\right){\displaystyle {\int }_{\Omega }{\left|U\right|}^4\text{d}x}+{\Vert U^0\Vert }^4.\end{array}$ (3.12)

Since ${\oplus }_{i=1}^{m}E\left({\mu }_i\right)$ and $E_0$ are finite dimensional spaces, there exists a sufficiently large $T_m>0$ , such that for every $U^{+}\in {\oplus }_{i=1}^{m}E\left({\mu }_i\right)$ , $U^0\in E^0$ ,

$T_m{\displaystyle {\int }_{\Omega }{\left|U^{+}\right|}^2\text{d}x}\ge \Vert L\Vert {\Vert U^{+}\Vert }^2,T_m{\displaystyle {\int }_{\Omega }{\left|U^0\right|}^2\text{d}x}\ge \frac{1}{2}{\Vert U^0\Vert }^2.$ (3.13)

Therefore, for $U\in {\oplus }_{i=-\infty }^{m}E\left({\mu }_i\right)$ ,

$\begin{array}{c}{J}_{\rho }\left(U\right)\le -\frac{\Vert L\Vert }{2}{\Vert U^{+}\Vert }^2-\frac{c}{2}{\Vert U^{-}\Vert }^2-\frac{1}{2}{\Vert U^0\Vert }^2+C\left(T_m\right){\displaystyle {\int }_{\Omega }{\left|U\right|}^4\text{d}x}+{\Vert U^0\Vert }^4\\ \le -\frac{b}{2}{\Vert U\Vert }^2+C_1\left(m\right){\Vert U\Vert }^4,\end{array}$ (3.14)

where $b=\min \left\{\Vert L\Vert ,c,1\right\}$ and $C_1\left(m\right)$ is a constant that depends on m. If $U\in {\oplus }_{i=-\infty }^{m}E\left({\mu }_i\right)$ , and $\Vert U\Vert ={\left(\frac{b}{4C_1\left(m\right)}\right)}^{\frac{1}{2}}$ , then $J_{\rho }\left(U\right)\le -\frac{b^2}{16C_1\left(m\right)}$ . Suppose $C_1\left(m\right)\ge m$ . Recall that for $n\ge 1$ , $d_n={\displaystyle {\sum }_{i=-n+1}^0{l}_i}$ , where $l_i$ is the dimension of $E\left({\mu }_i\right)$ . For simplicity, we denote $d_0=0$ . For each $k\in {\mathbb{Z}}^{+}$ , let $m=m_k$ be the unique integer such that $d_{m-1}<k\le d_m$ . For $i\ge 1$ , we assume that $E\left({\mu }_i\right)={\oplus }_{j=1}^{l_i}{E}_{i,j}$ , where $\dim E_{i,j}=1$ . Define

${\rho }_k={\left(\frac{b}{4C_1\left(m_k\right)}\right)}^{\frac{1}{2}},{\epsilon }_k=\frac{b^2}{16C_1\left(m_k\right)},$

and

$A_k=\left\{U\in \left(\underset{i=-\infty }{\overset{d_{m-1}}{\oplus }}E\left({\mu }_i\right)\right)\oplus \left(\underset{j=1}{\overset{k-d_{m-1}}{\oplus }}{E}_{m,j}\right)|\Vert U\Vert ={\rho }_k\right\}.$

Hence for any $k\in {\mathbb{Z}}^{+}$ and $n\ge 1$ , there exist ${\epsilon }_k>0$ , ${\rho }_k>0$ with ${\rho }_k\to 0$ , and a symmetric set $A_k\subset \left\{U\in X|\Vert u\Vert ={\rho }_k\right\}$ such that $\gamma \left(X_n\cap A_k\right)=d_n+k$ and ${\sup }_{X_n\cap A_k}{J}_{\rho }<-{\epsilon }_k$ .

By Theorem 2.1, $J_{\rho }$ has a sequence of nontrivial critical points $\left\{U_k\right\}$ with $\Vert U_k\Vert \to 0$ as $k\to \infty$ . Then there exists $k_0\in {\mathbb{Z}}^{+}$ such that ${\Vert U_k^0\Vert }^2<\rho$ for all $k\ge k_0$ , thus $\left\{U_k\right\}$ are also nontrivial critical points of J and therefore nontrivial solutions of (P') for all $k\ge k_0$ . By standard regularity theory, we have ${\Vert U_k\Vert }_{L^{\infty }}\to 0$ as $k\to \infty$ . Then there exists $k_1\ge k_0$ such that ${\Vert U_k\Vert }_{L^{\infty }}<\delta$ for all $k\ge k_1$ . Hence $\left\{U_k\right\}$ are also nontrivial solutions of (P) for all $k\ge k_1$ and the theorem is proved.

Acknowledgements

The authors would like to express their gratitude to the referee for his/her valuable comments and suggestions.

Funding

This work was supported by National Natural Science Foundation of China (11901270) and Shandong Provincial Natural Science Foundation (ZR2019BA019).

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References