No CrossRef data available.
Article contents
Measurements and Gδ-Subsets of Domains
Published online by Cambridge University Press: 20 November 2018
Abstract
In this paper we study domains, Scott domains, and the existence of measurements. We use a space created by D. K. Burke to show that there is a Scott domain  $P$ for which
$P$ for which 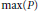 $\max (P)$ is a
$\max (P)$ is a 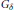 ${{G}_{\delta }}$-subset of
${{G}_{\delta }}$-subset of  $P$ and yet no measurement
$P$ and yet no measurement  $\mu $ on
$\mu $ on  $P$ has
$P$ has 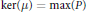 $\text{ker(}\mu \text{)}\,=\,\max (P)$. We also correct a mistake in the literature asserting that
$\text{ker(}\mu \text{)}\,=\,\max (P)$. We also correct a mistake in the literature asserting that 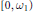 $[0,\,{{\omega }_{1}})$ is a space of this type. We show that if
$[0,\,{{\omega }_{1}})$ is a space of this type. We show that if  $P$ is a Scott domain and
$P$ is a Scott domain and 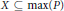 $X\,\subseteq \,\max (P)$ is a
$X\,\subseteq \,\max (P)$ is a 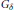 ${{G}_{\delta }}$-subset of
${{G}_{\delta }}$-subset of  $P$, then
$P$, then 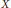 $X$ has a
$X$ has a 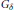 ${{G}_{\delta }}$-diagonal and is weakly developable. We show that if
${{G}_{\delta }}$-diagonal and is weakly developable. We show that if 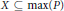 $X\,\subseteq \,\max (P)$ is a
$X\,\subseteq \,\max (P)$ is a 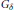 ${{G}_{\delta }}$-subset of
${{G}_{\delta }}$-subset of  $P$, where
$P$, where  $P$ is a domain but perhaps not a Scott domain, then
$P$ is a domain but perhaps not a Scott domain, then 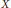 $X$ is domain-representable, first-countable, and is the union of dense, completely metrizable subspaces. We also show that there is a domain
$X$ is domain-representable, first-countable, and is the union of dense, completely metrizable subspaces. We also show that there is a domain  $P$ such that
$P$ such that 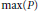 $\max (P)$ is the usual space of countable ordinals and is a
$\max (P)$ is the usual space of countable ordinals and is a 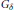 ${{G}_{\delta }}$-subset of
${{G}_{\delta }}$-subset of  $P$ in the Scott topology. Finally we show that the kernel of a measurement on a Scott domain can consistently be a normal, separable, non-metrizable Moore space.
$P$ in the Scott topology. Finally we show that the kernel of a measurement on a Scott domain can consistently be a normal, separable, non-metrizable Moore space.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011




