Assessing Quantum Calculation Methods for the Account of Ligand Field in Lanthanide Compounds
Abstract
:1. Introduction
2. Methods
3. Results and Discussion
3.1. The Multiconfigurational Account of Ligand Field Problems
3.2. Density Functional Account of Ligand Field Problems
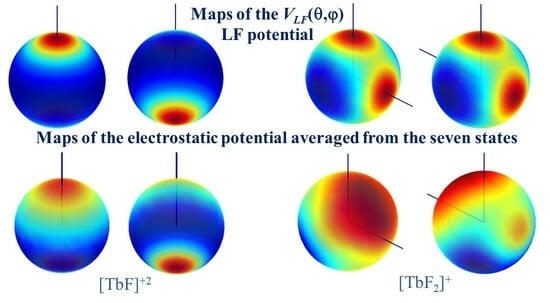
3.3. Revisiting the Crystal Field Electrostatic Approximation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ballhausen, C.J. Introduction to Ligand Field Theory; McGraw-Hill Book Co.: New York, NY, USA, 1962. [Google Scholar]
- Newman, D.J.; Ng, B.K.C. Crystal Field Handbook; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bethe, H. Termaufspaltung in Kristallen. Ann. Der Phys. 1929, 395, 133–208. [Google Scholar] [CrossRef]
- Van Vleck, J.H. Theory of the variations in paramagnetic anisotropy among different salts of the iron group. Phys. Rev. 1932, 41, 208–215. [Google Scholar] [CrossRef]
- Solomon, E.I.; Lever, A.B.P. Inorganic Electronic Structure and Spectroscopy: Methodology Volume I Edition; Wiley-Interscience: New York, NY, USA, 1999. [Google Scholar]
- Singh, S.K.; Eng, J.; Atanasov, M.; Neese, F. Covalency and chemical bonding in transition metal complexes: An ab initio based ligand field perspective. Coord. Chem. Rev. 2017, 344, 2–25. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Xiao, D.J.; Atanasov, M.; Long, G.J.; Grandjean, F.; Neese, F.; Long, J.R. Magnetic blocking in a linear iron(I) complex. Nat. Chem. 2013, 5, 577–581. [Google Scholar] [CrossRef] [PubMed]
- Wybourne, B.G. Spectroscopic Properties of Rare Earths; Wiley Interscience: New York, NY, USA, 1965. [Google Scholar]
- Griffith, J.S. The Theory of Transition-Metal Ions Reissue Edition; Cambridge University Press: London, UK, 1980. [Google Scholar]
- Cotton, F.A. Chemical Applications of Group Theory; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Jørgensen, C.K.; Pappalardo, R.; Schmidtke, H.H. Do the “ligand field” parameters in lanthanides represent weak covalent bonding? J. Chem. Phys. 1963, 39, 1422–1430. [Google Scholar] [CrossRef]
- Schäffer, C.E. Two symmetry parametrizations of the angular overlap model of the ligand field: Relation to the crystal field model. Struct. Bond. 1973, 14, 69–110. [Google Scholar]
- Deeth, R.J.; Gerloch, M. A cellular ligand-field study of the CuCl42− ion in Cs2[CuCl4]. J. Chem. Soc. Dalton Trans. 1986, 8, 1531–1534. [Google Scholar] [CrossRef]
- Schönherr, T.; Atanasov, M.; Adamsky, H. Angular overlap model. In Lever ABP; McCleverty, J.A., Meyer, T.J., Eds.; Comprehensive Coordination Chemistry II; Elsevier: Oxford, UK, 2003; Volume 2, pp. 443–455. [Google Scholar]
- Bridgeman, A.J.; Gerloch, M. A cellular ligand-field model for ‘l-l’ spectral intensities. Mol. Phys. 1993, 79, 1195–1213. [Google Scholar] [CrossRef]
- Gerloch, M.; Guy Woolley, R. The Functional Group in Ligand-Field Studies: The Empirical and Theoretical Status of the Angular Overlap Model. Progr. Inorg. Chem. 1984, 31, 371. [Google Scholar]
- Schonherr, T. Angular overlap model applied to transition metal complexes and dN-ions in oxide host lattices. Top. Curr. Chem. 1997, 191, 87–152. [Google Scholar]
- Bridgeman, A.J.; Gerloch, M. The interpretation of ligand field parameters. Progr. Inorg. Chem. 1997, 45, 179–281. [Google Scholar]
- Schonherr, T.; Atanasov, M.; Adamsky, H. Comprehensive Coordination Chemistry; Elsevier: Amsterdam, The Netherlands, 2003; Volume II, pp. 433–455. [Google Scholar]
- Urland, W. The assessment of the crystal-field parameters for f”-electron systems by the angular overlap model: Rare-earth ions in LiMF4. Chem. Phys. Lett. 1981, 77, 58–62. [Google Scholar] [CrossRef]
- Malta, O.L. A simple overlap model in lanthanide crystal-field theory. Chem. Phys. Lett. 1982, 87, 27–29. [Google Scholar] [CrossRef]
- García-Fuente, A.; Baur, F.; Cimpoesu, F.; Vega, A.; Jüstel, T.; Urland, W. Properties Design: Prediction and Experimental Validation of the Luminescence Properties of a New EuII-Based Phosphor. Chem. Eur. J. 2018, 24, 16276–16281. [Google Scholar] [CrossRef] [Green Version]
- Suta, M.; Cimpoesu, F.; Urland, W. The angular overlap model of ligand field theory for f elements: An intuitive approach building bridges between theory and experiment. Coord. Chem. Rev. 2021, 441, 213981. [Google Scholar] [CrossRef]
- Höppe, H.A. Recent developments in the field of inorganic phosphors. Angew. Chem. Int. Ed. 2009, 48, 3572–3582. [Google Scholar] [CrossRef]
- Dutczak, D.; Jüstel, T.; Ronda, C.; Meijerink, A. Eu2+ luminescence in strontium aluminates. Phys. Chem. Chem. Phys. 2015, 17, 15236–15249. [Google Scholar] [CrossRef] [Green Version]
- Suta, M.; Wickleder, C. Synthesis, Spectroscopic Properties and Applications of Divalent Lanthanides Apart from Eu2+. J. Lumin. 2019, 210, 210–238. [Google Scholar] [CrossRef]
- Jensen, F. Introduction to Computational Chemistry; John Wiley & Sons: West Sussex, UK, 2007. [Google Scholar]
- Koch, W.; Holthausen, M.C. A Chemist’s Guide to Density Functional Theory; Wiley-VCH: Berlin, Germany, 2001. [Google Scholar]
- Roos, B.O. The Complete Active Space Self-Consistent Field Method and its Applications in Electronic Structure Calculations. In Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry Part 2; Lawley, K.P., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; Volume 69. [Google Scholar]
- Nakano, H.; Nakayama, K.; Hirao, K.; Dupuis, M. Transition state barrier height for the reaction H2CO → H2 + CO studied by multireference Mo/ller–Plesset perturbation theory. J. Chem. Phys. 1997, 106, 4912. [Google Scholar] [CrossRef]
- Roos, B.O.; Andersson, K.; Fulscher, M.K.; Malmqvist, P.-A.; Serrano-Andres, L.; Pierloot, K.; Merchan, M. Multiconfigurational perturbation theory: Applications in electronic spectroscopy. Adv. Chem. Phys. 1996, 93, 219. [Google Scholar]
- Angeli, C.; Borini, S.; Cestari, M.; Cimiraglia, R. A quasidegenerate formulation of the second order n-electron valence state perturbation theory approach. J. Chem. Phys. 2004, 121, 4043–4049. [Google Scholar] [CrossRef] [PubMed]
- Bytautas, L.; Matsunaga, N.; Nagata, T.; Gordon, M.S.; Ruedenberg, K. Accurate ab initio potential energy curve of F2. II. Core-valence correlations, relativistic contributions, and long-range interactions. J. Chem. Phys. 2007, 127, 204301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bytautas, L.; Ruedenberg, K. Ab initio potential energy curve of F2. IV. Transition from the covalent to the van der Waals region: Competition between multipolar and correlation forces. J. Chem. Phys. 2009, 130, 164317. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef] [Green Version]
- Nalewajski, R.F. Kohn-Sham description of equilibria and charge transfer in reactive systems. Int. J. Quantum Chem. 1998, 69, 591–605. [Google Scholar] [CrossRef]
- Paulovic, J.; Cimpoesu, F.; Ferbinteanu, M.; Hirao, K. Mechanism of Ferromagnetic Coupling in Copper(II)-Gadolinium(III) Complexes. J. Am. Chem. Soc. 2004, 126, 3321–3331. [Google Scholar] [CrossRef]
- Putz, M.V.; Cimpoesu, F.; Ferbinteanu, M. Structural Chemistry, Principles, Methods, and Case Studies; Springer: Cham, Switzerland, 2018; pp. 389–675. [Google Scholar]
- Ferbinteanu, M.; Kajiwara, T.; Choi, K.-Y.; Nojiri, H.; Nakamoto, A.; Kojima, N.; Cimpoesu, F.; Fujimura, Y.; Takaishi, S.; Yamashita, M. A Binuclear Fe(III)Dy(III) Single Molecule Magnet. Quantum Effects and Models. J. Am. Chem. Soc. 2006, 128, 9008–90009. [Google Scholar] [CrossRef]
- Cimpoesu, F.; Dahan, F.; Ladera, S.; Ferbinteanu, M.; Costes, J.-P. Chiral Crystallization of a Heterodinuclear Ni-Ln Series: Comprehensive Analysis of the Magnetic Properties. Inorg. Chem. 2012, 51, 11279–11293. [Google Scholar] [CrossRef]
- Gao, Y.; Viciano-Chumillas, M.; Toader, A.M.; Teat, S.J.; Ferbinteanu, M.; Tanase, S. Cyanide-bridged coordination polymers constructed from lanthanide ions and octacyanometallate building-blocks. Inorg. Chem. Front. 2018, 5, 1967–1977. [Google Scholar] [CrossRef]
- Aravena, D.; Atanasov, M.; Neese, F. Periodic Trends in Lanthanide Compounds through the Eyes of Multireference ab Initio Theory. Inorg. Chem. 2016, 55, 4457–4469. [Google Scholar]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Bykov, D.; Ganyushin, D.; Hansen, A.; Izsak, R.; Liakos, D.G.; Kollmar, C.; Kossmann, S.; et al. An Ab Initio, DFT, and Semiempirical SCF-MO Package-Version 3.0.; Design and Scientific Directorship; Max Planck Institute for Bioinorganic Chemistry: Mulheim an der Ruhr, Germany, 2012. [Google Scholar]
- Atanasov, M.; Ganyushin, D.; Sivalingam, K.; Neese, F. A Modern First-Principles View on Ligand Field Theory through the Eyes of Correlated Multireference Wavefunctions. In Molecular Electronic Structures of Transition Metal Complexes II in Structure and Bonding; Mingos, D.M.P., Day, P., Dahl, J.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 143, pp. 149–220. [Google Scholar]
- Ferbinteanu, M.; Stroppa, A.; Scarrozza, M.; Humelnicu, I.; Maftei, D.; Frecus, B.; Cimpoesu, F. On the Density Functional Theory Treatment of Lanthanide Coordination Compounds: A Comparative Study in a Series of Cu-Ln (Ln = Gd, Tb, Lu) Binuclear Complexes. Inorg. Chem. 2017, 56, 9474–9485. [Google Scholar] [CrossRef] [PubMed]
- Atanasov, M.; Daul, C.A. Modeling properties of molecules with open d-shells using density functional theory. C. R. Chim. 2005, 8, 1421–1433. [Google Scholar] [CrossRef] [Green Version]
- Atanasov, M.; Daul, C.A.; Rauzy, C. Optical Spectra and Chemical Bonding in Inorganic Compounds. In Structure and Bonding; Mingos, D.M.P., Schonherr, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 106, pp. 97–125. [Google Scholar]
- Ramanantoanina, H.; Cimpoesu, F.; Gottel, C.; Sahnoun, M.; Herden, B.; Suta, M.; Wickleder, C.; Urland, W.; Daul, C. Prospecting Lighting Applications with Ligand Field Tools and Density Functional Theory: A First-Principles Account of the 4f7-4f65d1 Luminescence of CsMgBr3:Eu2+. Inorg. Chem. 2015, 54, 8319–8326. [Google Scholar] [CrossRef] [PubMed]
- Ramanantoanina, H.; Urland, W.; Herden, B.; Cimpoesu, F.; Daul, C. Tailoring the optical properties of lanthanide phosphors: Prediction and characterization of the luminescence of Pr3+-doped LiYF4. Phys. Chem. Chem. Phys. 2015, 17, 9116–9125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- García-Fuente, A.; Cimpoesu, F.; Ramanantoanina, H.; Herden, B.; Daul, C.; Suta, M.; Wickleder, C.; Urland, W. A ligand field theory-based methodology for the characterization of the Eu2+ [Xe]4f65d1 excited states in solid state compounds. Chem. Phys. Lett. 2015, 622, 120–123. [Google Scholar] [CrossRef]
- Ramanantoanina, H.; Sahnoun, M.; Barbiero, A.; Ferbinteanu, M.; Cimpoesu, F. Development and applications of the LFDFT: The non-empirical account of ligand field and the simulation of the f-d transitions by density functional theory. Phys. Chem. Chem. Phys. 2015, 17, 18547–18557. [Google Scholar] [CrossRef] [Green Version]
- Ramanantoanina, H.; Urland, W.; Garcia-Fuente, A.; Cimpoesu, F.; Daul, C. Ligand Field Density Functional Theory for the prediction of future domestic lighting. Phys. Chem. Chem. Phys. 2014, 16, 14625–14634. [Google Scholar] [CrossRef] [Green Version]
- Ramanantoanina, H.; Urland, W.; Cimpoesu, F.; Daul, C. The Angular Overlap Model extended for two-open-shell f and d electrons. Phys. Chem. Chem. Phys. 2014, 16, 12282–12290. [Google Scholar] [CrossRef] [Green Version]
- Ramanantoanina, H.; Urland, W.; García-Fuente, A.; Cimpoesu, F.; Daul, C. Calculation of the 4f1 → 4f0d1 transitions in Ce3+-doped systems by Ligand Field Density Functional Theory. Chem. Phys. Lett. 2013, 588, 260–266. [Google Scholar] [CrossRef]
- Ramanantoanina, H.; Urland, W.; Cimpoesu, F.; Daul, C. Ligand field density functional theory calculation of the 4f2 → 4f15d1 transitions in the quantum cutter Cs2KYF6:Pr3+. Phys. Chem. Chem. Phys. 2013, 15, 13902–13910. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular Orbital Methods. 9. Extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724. [Google Scholar] [CrossRef]
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931. [Google Scholar] [CrossRef]
- Baerends, E.J.; Ziegler, T.; Atkins, A.J.; Autschbach, J.; Baseggio, O.; Bashford, D.; Bérces, A.; Bickelhaupt, F.M.; Bo, C.; Boerrigter, P.M.; et al. ADF2019, SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2019. [Google Scholar]
- MATLAB; Version 6.0; The MathWorks Inc.: Natick, MA, USA, 2000.
- Eaton, J.W.; Bateman, D.; Hauberg, S.; Wehbring, R. GNU Octave, version 3.8.1; Samurai Media Limited: Portsmouth, UK, 2014. [Google Scholar]
- Wolfram Research, Inc. Mathematica; Wolfram Research, Inc.: Champaign, IL, USA, 2014. [Google Scholar]
- Wolfram, S. The Mathematica Book, 5th ed.; Wolfram-Media: Champaign, IL, USA, 2003. [Google Scholar]
- Slater, J.C. The theory of complex spectra. Phys. Rev. 1929, 34, 1293–1322. [Google Scholar] [CrossRef]
- Tondello, E.; De Michelis, G.; Oleari, L.; Di Sipio, L. Slater-Condon parameters for atoms and ions of the first transition period. Coord. Chem. Rev. 1967, 2, 53–63. [Google Scholar] [CrossRef]
- Racah, G. Theory of Complex Spectra II. Phys. Rev. 1942, 62, 438–462. [Google Scholar] [CrossRef]
- Jin, J.; Yu, H.; Guo, L.; Liu, J.; Wu, B.; Guo, Y.; Fu, Y.; Zhao, L. Crystallographic and Spectroscopic Evidence for Intrinsic Distortion in the Disordered Crystal β-NaGdF4. Phys. Chem. Chem. Phys. 2018, 20, 15835–15840. [Google Scholar] [CrossRef]
- Yamamoto, S.; Tatewaki, H. Assignment of electronic spectra of GdF by identifying families using the f-shell Omega decomposition method. Comput. Theor. Chem. 2012, 980, 37–43. [Google Scholar] [CrossRef]
- Tatewaki, H.; Yamamoto, S.; Moriyama, H. Low-Lying Excited States of Lanthanide Diatomics Studied by Four-Component Relativistic Configuration Interaction Methods. In Computational Methods in Lanthanide and Actinide Chemistry; Dolg, M., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015; pp. 89–119. [Google Scholar]
- Schäffer, C.F. The Angular Overlap Model Applied to Chiral Chromophores and the Parentage Interrelation of Absolute Configurations. Proc. R. Soc. A 1967, 297, 96–133. [Google Scholar]
- Schäffer, C.F. A ligand field approach to orthoaxial complexes. Theoret. Chim. Acta 1966, 4, 166–173. [Google Scholar] [CrossRef]
- Richardson, F.S.; Reid, M.F.; Dallara, J.J.; Smith, R.D. Energy levels of lanthanide ions in the cubic Cs2NaLnCl6 and Cs2NaYCl6: Ln3+ (doped) systems. J. Chem. Phys. 1985, 83, 3813. [Google Scholar] [CrossRef]
- Tanner, P.; Duan, C.-K.; Cheng, B.-M. Excitation and Emission Spectra of Cs2NaLnCl6 Crystals Using Synchrotron Radiation. Spectrosc. Lett. 2010, 43, 431–445. [Google Scholar] [CrossRef]
- Schiffbauer, D.; Wickleder, C.; Meyer, G.; Kirm, M.; Stephan, M.; Schmidt, P.C. Crystal structure, electronic structure, and luminescence of Cs2KYF6: Pr3+. Z. Für Anorg. Allg. Chem. 2005, 631, 3046. [Google Scholar] [CrossRef]
- Urland, W. “Magnetochemical Series” for Lanthanoid Compounds. Angew. Chem. Int. Ed. Engl. 1981, 20, 210. [Google Scholar] [CrossRef]
- Perdew, J.P.; Parr, R.G.; Levy, M.; Balduz, J.L. Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy. Phys. Rev. Lett. 1982, 49, 1691–1694. [Google Scholar] [CrossRef]
- Gross, E.K.; Oliveira, L.N.; Kohn, W. Density-functional theory for ensembles of fractionally occupied states. I. Basic formalism. Phys. Rev. A 1988, 37, 2809–2820. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electronic Gas. Phys. Rev. 1964, 136, 864–871. [Google Scholar] [CrossRef] [Green Version]
- Wesolowski, T.A.; Warshel, A. Frozen Density Functional Approach for ab-initio Calculations of Solvated Molecules. J. Phys. Chem. 1993, 97, 8050. [Google Scholar] [CrossRef]
- Jacob, C.R.; Neugebauer, J.; Visscher, L. A flexible implementation of frozen-density embedding for use in multilevel simulations. J. Comput. Chem. 2008, 29, 1011. [Google Scholar] [CrossRef]
- Van Lenthe, E.V.; Snijders, J.G.; Baerends, E.J. The zero-order regular approximation for relativistic effects: The effect of spin–orbit coupling in closed shell molecules. J. Chem. Phys. 1996, 105, 6505–6516. [Google Scholar] [CrossRef] [Green Version]






| [TbF]+2 | efδ(F) | efπ(F) | efσ(F) | |
|---|---|---|---|---|
| Restricted | MO energies | 2984.3 | 5750.9 | 6944.6 |
| Frozen LF configurations | −1202.6 | 6991.4 | 4948.3 | |
| Iterative LF configurations | −851.7 | 2710.1 | 5372.6 | |
| Frozen density MOs | 500.1 | 879.2 | 1032.4 | |
| Unrestricted | α MO energies | 2201.9 | 4549.1 | 4315.2 |
| β MO energies | 2387.5 | 3218.2 | 5258.9 | |
| Frozen LF configurations | −1857.5 | −738.0 | 5171.7 | |
| Iterative LF configurations | −1424.4 | −292.0 | 1554.3 | |
| Frozen density α MOs | 459.7 | 806.6 | 959.8 | |
| Frozen density β MOs | 540.4 | 951.8 | 1121.1 |
| [TbF2]+ | efδ(F) | efπ(F) | efσ(F) | |
|---|---|---|---|---|
| Restricted | MO energies | 1770.4 | 3722.3 | 4920.1 |
| Frozen LF configurations | −382.3 | 2189.05 | 4441.8 | |
| Iterative LF configurations | −128.25 | 2211.6 | 4218.4 | |
| Frozen density MOs | 556.5 | 988.1 | 1193.7 | |
| Unrestricted | α MO energies | 1290.5 | 2355.2 | 2661.7 |
| β MO energies | 1318.7 | 2621.4 | 3472.3 | |
| Frozen LF configurations | −846.9 | 740.4 | 2123.3 | |
| Iterative LF configurations | −572.3 | 831.6 | 1971.7 | |
| Frozen density α MOs | 512.2 | 907.4 | 1096.9 | |
| Frozen density β MOs | 604.9 | 1096.9 | 1330.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toader, A.M.; Frecus, B.; Oprea, C.I.; Buta, M.C. Assessing Quantum Calculation Methods for the Account of Ligand Field in Lanthanide Compounds. Physchem 2023, 3, 270-289. https://doi.org/10.3390/physchem3020019
Toader AM, Frecus B, Oprea CI, Buta MC. Assessing Quantum Calculation Methods for the Account of Ligand Field in Lanthanide Compounds. Physchem. 2023; 3(2):270-289. https://doi.org/10.3390/physchem3020019
Chicago/Turabian StyleToader, Ana Maria, Bogdan Frecus, Corneliu Ioan Oprea, and Maria Cristina Buta. 2023. "Assessing Quantum Calculation Methods for the Account of Ligand Field in Lanthanide Compounds" Physchem 3, no. 2: 270-289. https://doi.org/10.3390/physchem3020019