- Research Center for Economy of Upper Reaches of the Yangtze River, Chongqing Technology and Business University, Chongqing, China
Objective: Scientifically organizing emergency rescue activities to reduce mortality in the early stage of earthquakes.
Methods: A robust casualty scheduling problem to reduce the total expected death probability of the casualties is studied by considering scenarios of disrupted medical points and routes. The problem is described as a 0-1 mixed integer nonlinear programming model. An improved particle swarm optimization (PSO) algorithm is introduced to solve the model. A case study of the Lushan earthquake in China is conducted to verify the feasibility and effectiveness of the model and algorithm.
Results: The results show that the proposed PSO algorithm is superior to the compared genetic algorithm, immune optimization algorithm, and differential evolution algorithm. The optimization results are still robust and reliable even if some medical points fail and routes are disrupted in affected areas when considering point-edge mixed failure scenarios.
Conclusion: Decision makers can balance casualty treatment and system reliability based on the degree of risk preference considering the uncertainty of casualties, to achieve the optimal casualty scheduling effect.
1. Introduction
Earthquakes often occur randomly without warning and bring devasting damages to affected areas. Earthquakes not only cause serious economic losses but also lead to many people's injuries or even death (1, 2). Statistically, the 1976 Tangshan earthquake caused 242,769 deaths and 435,556 injuries. The 2008 Wenchuan earthquake killed 69,227 people, injured 374,643 people, and left 17,923 people missing. After a large-scale destructive earthquake, the number of casualties increases rapidly, the injury states are complicated, and the affected areas are wide. The scientific and effective treatment of the casualties is the primary task of the post-disaster relief work, and its efficiency is related to the success or failure of the post-disaster rescue. Especially the early stage of post-earthquake relief is the critical period for emergency rescue and disaster relief (3). How to organize rescue activities plays a crucial role during this golden rescue period, such as transporting and treating the casualties (4). Consequently, utilizing existing medical resources to build an efficient and reliable emergency logistics network to transport the casualties to medical points efficiently for treatment is an urgent problem to be resolved in the early post-earthquake period.
The problem of casualty transportation scheduling was usually described as an emergency facility location-allocation problem or a delivery vehicle routing problem (5–8). On this basis, some studies considered the type of casualties (9, 10) or the deterioration of the wounded (11) to further optimize the casualty scheduling. However, the above literature generally contained an implicit assumption that the facility was completely reliable without disruption. This assumption did not correspond to reality. Especially in the post-earthquake emergency logistics system, the facilities and routings are easy to fail due to the impact of earthquake disasters and their secondary disasters. The disruption factors were considered in some literature (12–14).
To sum up, researchers have carried out in-depth research on the optimization of emergency scheduling for casualty transportation after earthquake disasters, but there are still some problems that are required further study. Firstly, most of the existing research studied the problem of injury deterioration and casualty scheduling alone without considering the two problems simultaneously. Secondly, most of the current studies assumed that the road and facilities in the earthquake disaster logistics network were completely reliable without failures. Although some literature considered road disruption or facility failures, there are few works considering the mixed failure state of points (facility) and edges (route) in the emergency logistics network simultaneously. Thirdly, existing studies usually assumed that information such as the number of casualties was determined or described as fuzzy parameters. In reality, such a number cannot be estimated exactly. To fill up this gap, this paper considers the point-edge mixed failure scenario, combines the evolution of injury situation, adopts the robust optimization method to deal with the uncertain amounts of casualties, and further studies the optimization problem of casualty transport scheduling in the early stage of post-earthquake relief.
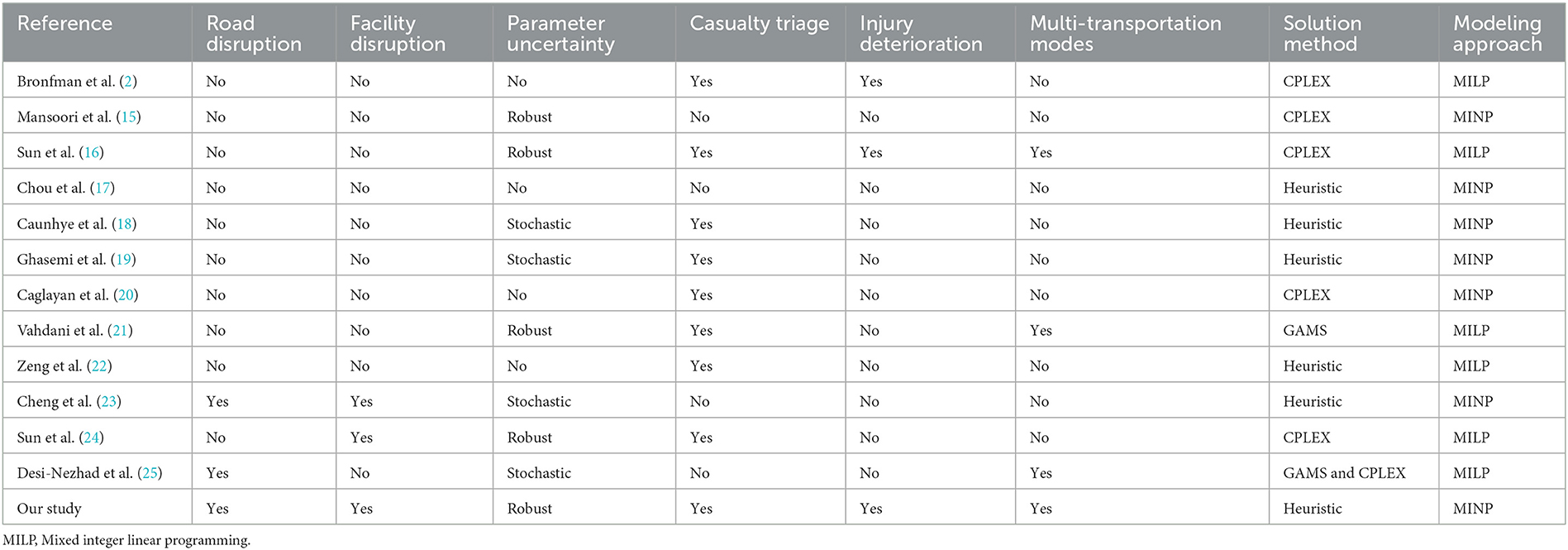
The main differences between this paper and previous studies are summarized in Table 1. More specifically, the contributions of this paper are as follows. (1) We propose a new casualty scheduling robust optimization problem for post-earthquake relief. As mentioned in the previous subsection, the proposed problem considers some new characteristics in the early stage of post-earthquake relief, such as point-edge mixed failure scenarios, injury deterioration, and multiple transportation modes. (2) A mixed integer non-linear programming (MINP) model is established to formulate the proposed problem. (3) According to the characteristics of the model, an improved integer-encoded particle swarm optimization (PSO) algorithm is designed in this paper. The improved PSO is compared with the genetic algorithm (GA), immune algorithm (IA), and differential evolution algorithm (DE).
2. Literature review
This section will review relevant literature in the following three categories.
2.1. Traditional casualty scheduling problems
The problem of casualty transportation scheduling is usually described as an emergency facility location-allocation problem or a delivery vehicle routing problem (5–8). Mansoori et al. (15) proposed a multi-objective humanitarian supply chain design problem that minimizes the total number of injured not transferred to hospitals. Fiedrich et al. (26) proposed a dynamic optimization model where the total number of fatalities during the initial search-and-rescue period after strong earthquakes is minimized. Andersson et al. (27) established a support tool for dynamic ambulance relocation and automatic ambulance dispatching. Xie et al. (28) formulated a lane-based evacuation network optimization problem that integrates lane reversal and crossing elimination strategies. A Lagrangian relaxation algorithm based on the principles of Tabu search is designed to solve the model. Mclay et al. (29) proposed an improved Markov decision model to optimize ambulance dispatch dynamically to maximize the number of critically injured patients. Knyazkov et al. (30) studied the present situation of emergency transport for patients with acute coronary heart disease in St. Petersburg. The optimization of ambulance routes was proposed according to the road network in the city, to improve the number of ambulances per capita and the speed of ambulance response in this work. Sung et al. (31) transformed the problem of treating the injured after a disaster into the dispatching problem of emergency ambulances with the goal of maximizing the expected survival rate and designed a column generation algorithm. Repoussis et al. (32) proposed a mixed integer programming formulation for the combined ambulance dispatching, patient-to-hospital assignment, and treatment ordering problem. The objectives are to minimize the overall response time and the total flow time required to treat all patients. Shavarani et al. (33) described how to properly allocate existing emergency vehicles to hospitals and effectively plan vehicle routes after a disaster in a densely populated area, to maximize patient survival. Sun et al. (16) proposed an emergency model of the location-transportation-allocation problem. The objective is to minimize the total cost and the sum of injury severity scores. The integrated research on the problem of casualty scheduling and emergency facility location is studied in some literature (34, 35). Sheu et al. (36) proposed a method for designing a seamless centralized emergency supply network. A three-stage multi-objective (travel distance minimization, operational cost minimization, and psychological cost minimization) mixed-integer linear programming model is built to describe the problem. Hu et al. (37) proposed a mixed integer programming model that considers the uncertainty of the number of injured people and integrates the decision of locating shelters and transferring injured people. Chou et al. (17) proposed a patient transportation and assignment model considering the routing of ambulances and operational conditions of hospitals.
2.2. Casualty scheduling problems considering wounded types
A large number of wounded personnel emerged in the early stage after an earthquake, thus it is important to dispatch the wounded personnel considering the wounded type (9, 10). Caunhye et al. (18) constructed a three-stage stochastic programming model to locate alternative care facilities and allocate casualties. The model integrates casualty triage and the movement of self-evacuees. Ghasemi et al. (19) proposed a stochastic multi-objective mixed-integer mathematical programming for logistic distribution and evacuation planning during an earthquake. Na et al. (38) classified the wounded according to the results of the field diagnosis of the wounded, combined with the medical resources required by different wounded, assigned rescue vehicles to the wounded, and established a mixed integer linear programming model with cost minimization as the objective function. Talarico et al. (39) classified the injured into two categories: those that can be treated at local sites and those that must be treated in hospitals. They established an optimization model of ambulance routing decisions, aiming at minimizing the weighted waiting time of the injured, and solved the model with a large-scale neighborhood search algorithm. Rezapour et al. (40) divided the injured in each disaster area into yellow and red grades and studied how to reasonably allocate search and rescue personnel and medical personnel to the disaster area. More studies are available in literature (41, 42). The condition of the wounded deteriorates over time in reality. Wilson et al. (43) proposed a Markov chain model for the injury state transfer of casualties. Jin et al. (11) proposed an optimization model for patient delivery and medical resource allocation with capacity restrictions considering the severity of injuries. Liu et al. (44) set up a double objective optimization model for temporary medical service point location and the optimal medical service allocation decisions considering the deterioration of injury. The goals are to maximize the expected number of survival and minimize the total operation cost.
2.3. Casualty scheduling problems considering disruptions
The facilities (points) and the roads (edges) of an emergency logistics network might be disrupted after a large-scale earthquake. The logistics network design problem considering facility failures is studied in some literature. Bayram et al. (45) studied the shelter location and evacuation route assignment problem considering the disruption/degradation of the evacuation road network structure. Cheng et al. (23) adopted a two-stage robust optimization framework to study the robust fixed cost location problem in the case of uncertain demand and facility disruption, and developed a column constraint generation algorithm to accurately solve the model. Zhou et al. (46) constructed a location-allocation model for emergency facilities suitable for the initial stage of post-earthquake rescue, considering facility disruption and multiple types of fuzzy demand. Mohammadi et al. (47) studied a multi-objective reliable optimization model to organize a humanitarian relief chain. They made a broad range of decisions, including reliable facility location-allocation, fair distribution of relief items, assignment of victims, and routing of trucks. Sun et al. (24) proposed a scenario-based robust dual-objective optimization model to study the location of medical facilities, casualty transport, and relief material distribution under the temporary medical point failure scenarios. There are also some studies on the design of emergency logistics networks considering edge (road network) failures. Sabouhi et al. (48) proposed a comprehensive stochastic programming model for the distribution of relief materials in disaster areas, taking the demand and disrupted roads as uncertain parameters. Gong et al. (49) studied the decision optimization of patient scheduling in the early stage of post-earthquake rescue, considering the factors such as the deterioration of the injured and road disruption. Desi-Nezhad et al. (25) developed a two-stage stochastic programming model to transport injured people with consideration of multiple disruptions at transportation links and facilities.
3. Description of injury deterioration
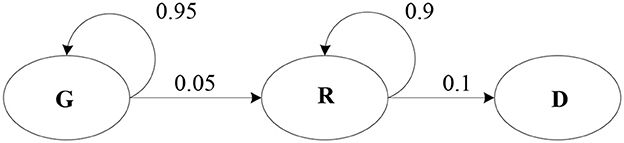
The injury deterioration can be described by a Markov chain proposed by Wilson et al. (43). The injury state of the wounded evolves toward the direction of gradual aggravation or continues to maintain the original state, with a certain probability in the process of waiting for rescue. And death is the end of the injury evolution in process. If the injury at the current stage is severe, the injury may be transferred to the death state or remain severe if effective treatment is not available at the next stage. If the injury is minor at the current stage, the injury may be transferred to severe or remain minor if no rescue is available at the next stage. It can be seen from the evolution of the injury state that the state transfer is stochastic, and the state of the wounded at the next stage only depends on the current state independent of the historical state, which is consistent with the no aftereffect of the Markov process. Therefore, the evolution of the injury has a Markov character.
In this paper, the evolution process of injury is divided into three finite-state Markov processes: minor injury (Green, G), severe injury (Red, R), and death (D). The process is repeated until the casualty dies or is saved. Let the initial time t = 0. All rescue teams are ready at the initial time. The injury level of the casualty is randomly and unidirectionally changed once per minute without any medical treatment, as shown in Figure 1.
It is assumed that there is a linear relationship between the severity of injury and the time before the wounded is treated. According to the random transfer probability between the injury states, the possible death probability of the casualty j whose initial injury state is R is expressed as formula (1).
In expression (1), indicates the time required to transport a severe casualty from the affected point i to the medical point j. Lr represents the injury state of the casualty in the initial time is r. prd indicates the probability that a casualty's injury state changes from severe to death and let prd = 0.1 in this article referring to literature (43).
If , the wounded may die in a waiting process. The death probability of the severe casualty while waiting for rescue can be expressed by Equation (2).
The death probability of the minor casualty can be written by the transition probability equation. That is, the probability of changing from a minor injury to a severe injury is calculated first, and then the probability of deteriorating from the severe injury to death is calculated. The time T that the wounded fully evolves from G to R should be first judged when calculating the death probability. According to Figure 1, the transition probability from state G to R is 0.05. Let 0.05*T = 1, then, T = 20 when G evolves into R. When the ambulance arrival time is <20 units, the wounded does not evolve to death, and the death probability is 0. When the arrival time of the ambulance is >20 units, the death probability in this state is . So, the probability function of death in a minor state is a time-segment function, see expression (3).
Therefore, the death probability functional of a casualty can be expressed as (4).
4. Model
4.1. Problem description
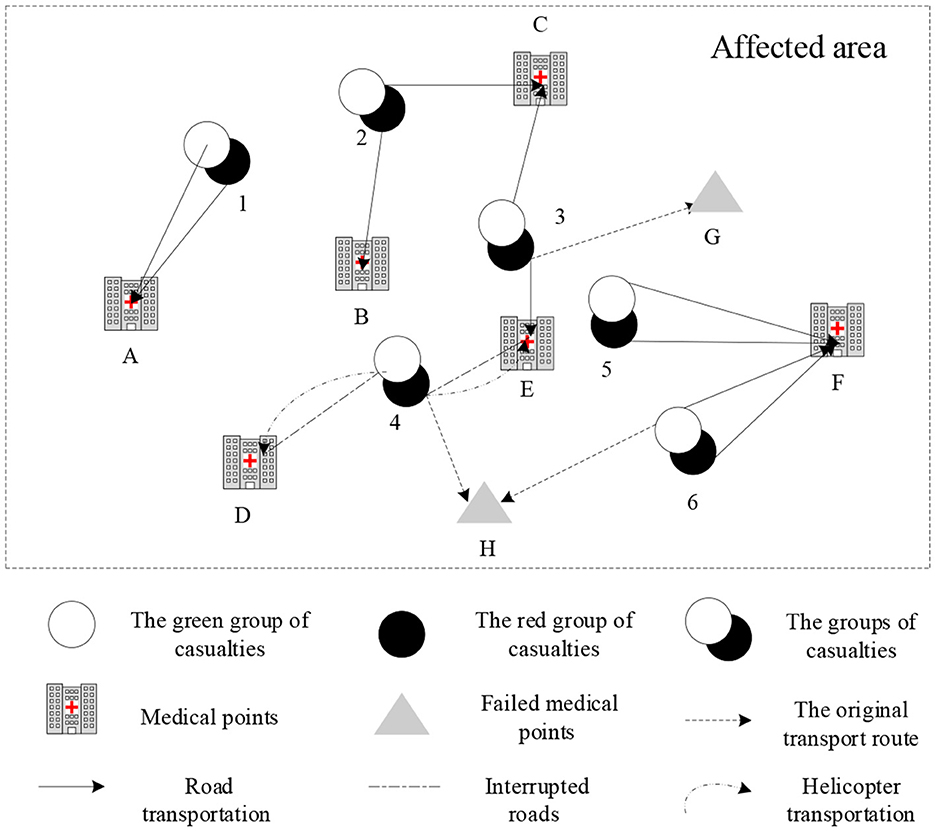
The impact of aftershocks, mudslides, and other secondary disasters, not only leads to medical points failure but also causes road damage or interruption, in the early stage of post-earthquake relief. There is a mixed failure of facility nodes and routes in the emergency logistics network. The transport network diagram with the point-edge mixed failures in the early stage of post-earthquake relief is shown in Figure 2. As can be seen from Figure 2, based on the failures of facility points H and G, the secondary disaster also leads to the interruption of roads between affected point 4 and medical point D, and between affected point 4 and medical point E. At this time, ambulances cannot normally pass on the two roads, so it is necessary to use helicopters to transport the wounded to ensure timely treatment, reduce the death rate of the wounded, and improve the efficiency of emergency rescue.
The purpose of emergency rescue is to treat as many casualties as possible in the shortest time and reduce the death rate of the wounded. Therefore, the goal of the model is to minimize the expected death probability of casualties.
4.2. Assumptions
Model assumptions are as follows. First, the location of affected points and medical points is known, and the resources available at the medical point are limited. Second, each medical point can serve multiple casualty groups at the same time, and each casualty group can be assigned just one medical point. Third, the casualty groups have been classified in advance according to the trauma index of the injured. The severe injuries should be treated first according to the medical resources and ambulance and helicopter transport conditions. Four, each ambulance can only transport two casualties at a time, and each helicopter can transport four casualties at a time.
4.3. Notations
The parameters are as follows.
I: Set of affected points, i ∈ I;
J: Set of medical points, j ∈ J;
S: Set of Scenarios, s ∈ S;
R:The severe state of casualties (marked as red);
G:The minor injury state of casualties (marked as green);
W:Set of injury states,;
:The death probability of casualties;
H: Set of ambulances, h ∈ H;
N: Set of rescue helicopters, n ∈ N;
M: A large positive integer number;
dij: Transportation distance from affected point i to medical point j;
εij: Degree of route damage between affected point i and medical point j; if εij > 0.5, the route is disrupted, and the ambulances cannot pass. Then, the helicopter transportation should be considered. With the support of modern remote sensing technology and communication technology, the damage degree of route in the early stage after earthquake can be sensed in real time without constant trial and error.
: Generalized transportation distance from affected point i to medical point j. The more damaged the route, the slower the vehicle speed, and the longer the transport time. That is, the longer the . can be obtained according to the method mentioned in literature (50), as .
tij: The time taken to transport the wounded from affected point i to medical point j;
T: The horizon of scheduling time,∀t ∈ T;
: The waiting time for ambulances or helicopters rescue for a casualty with injury state w;
vh: The speed of ambulance h;
vn: The speed of helicopter n;
Qj: The number of available resources at medical point j;
Qh: The number of available ambulance h at medical points;
Qn: The number of available helicopter n at medical points;
qh: The number of casualties can be transported by ambulance h at one time;
qn: The number of casualties can be transported by helicopter n at one time;
Cw: Resources needed to treat a casualty with injury state w, W = {w|w = r, g};
a: Number of times an ambulance or a helicopter arrived at an affected point;
fiw: The number of casualties with injury state w in affected point i;
βjs: βjs = 0 represents the medical point j fail in scenario s; otherwise βjs = 1.
The decision variables are as follows.
kijw: The number of casualties with injury state w transported from affected point i to medical point j;
Xij: A binary variable. If medical point j allocated to affected point i, Xij = 1; otherwise Xij = 0;
Xi′j: A binary variable. If medical point j reallocated to affected point i′ after the initial allocated medical point j′ failed, ;otherwise ;
: A binary variable. If ambulance h travels from affected point i′ to medical point j after the initial allocated medical point j′ failed, ; otherwise ;
: A binary variable. If ambulance h travels from affected point i′ to medical point j after the initial allocated medical point j′ failed, Yijh = 1; otherwise Yijh = 0;
Zijn: A binary variable. If helicopter n travels from affected point i to medical point j, Zijn = 1; otherwise Zijn = 0;
: A binary variable. If helicopter n travels from affected point i′ to medical point j after the initial allocated medical point j′ failed, ; otherwise .
4.4. Mathematical formulation
The mathematical model can be formulated as follows.
The objective function (5) is to minimize the total expected death probability of casualties. Constraint (6) denotes the death probability of casualties with different injury states. Constraint (7) is the resource limitation of medical points. Constraint (8) denotes the initial resources of medical points. Constraint (9) denotes the restriction of available resources at medical points at time t. Constraints (10) and (11) denote the restrictions on the number of available ambulances and helicopters from affected points to medical points respectively. Constraints (12) and (13) denote the waiting time for casualties with injury state g and r, respectively. Constraint (14) denotes the transportation distances from affected points to medical points. Constraint (15) denotes the time taken to transport casualties from affected points to medical points. Constraint (16) denotes each affected point will be served by the nearest open backup medical point if its initial allocated medical point has failed. Constraint (17) is a 0–1 variables restriction.
4.5. A robust optimization model
As the destructive earthquake occurred suddenly, and aftershocks may result in injuries in the initial stage after an earthquake, the number of casualties in affected points cannot be accurately estimated. Therefore, robust optimization was used to deal with the number of casualties to reduce the risk caused by uncertainty.
The parameter Γiw and corresponding variables are introduced to process the objective function and constraint Referring (51). Objective function equation (5) has uncertain variables of fiw. Define the value range of as . fiw is the nominal value of uncertain number of casualties. is the maximum deviation of the uncertain number of casualties. We introduce variable f to transform the objective function (5) referring to (52). The objective function (5) is equivalent to (18)–(19).
A protection function for the number of casualties is introduced here as equation (20). Γiw is the control coefficient of the number of casualties.
A protection function for the number of casualties is introduced here as equation (20). Γiw is the control coefficient of the number of casualties. Γiw ∈ [0, |Jiw|]. Where Jiw is the number of Γiw. The objective of this robust method is that the number of casualties varies within their interval at most ⌊Γiw⌋ affected points. Γiw is the balance between robustness and optimality. The bigger the Γiw, the more conservative the mode. The protection function for the number of casualties is introduced as with φ(X, Γiw) consideration of the uncertainty of the number of casualties. The objective function (5) can be transformed into formula (20).
Where, Siw represents the group set of the maximum number of casualties deviating from the nominal value. When Γiw = 0, ∀i, w, the robust model is equivalent to the nominal model.
Formula (20) can be expressed as (21).
If Γiw, ∀i, w is a integer,Γiw = ⌊Γiw⌋, ∀i, w, then
If Γiw = 0, ∀i, w,all the number of casualties are nominal. When Γiw = γ, the number of casualties in all injury states deviates from the nominal values, the model is equivalent to the Soyster model. As Γiw changes, the conservatism of the model also changes accordingly. The objective function (5) can be finally transformed into the following expressions based on the strong duality.
Therefore, the robust optimization model considering the uncertain number of casualties can be given as follows.
5. Algorithm
The built model is a 0–1 mixed integer non-linear programming model, which cannot be solved by exact algorithms such as branch and bound algorithm or operations research software such as CPLEX. An improved integer-coded PSO algorithm is designed to solve the model.
The algorithm steps are described as follows.
5.1. Population initialization
① Initialization of parameters: Set population size as popsize, maximum iterations as maxgen, learning factors as c1 and c2, inertia weight as w.
② Particle encoding and decoding: Supposing there are n casualty groups and k medical points in the model, each particle has a code length of n. Each position of the particle is a positive integer randomly generated between 1 and k, and denotes the relation of assign between a casualty group and a medical point. Taking Figure 3 for example, there are 6 medical points in the affected area, which are required to provide rescue services to 11 casualty groups. The length of the particle is 11. Casualty group 2 and 11 are assigned to medical point 1, casualty group 1 and 10 are assigned to medical point 2, and so on.
③ Initialization of the best value of individuals and groups: The initial location and velocity of particles can be randomly generated. The fitness value of the current population can be calculated by the fitness function. The fitness function is the objective function (25). The individual position is the optimal position of the current individual Pbest. The minimum value of the current particle Pbest_value is the initial optimal value of individuals that can be got by comparing the optimal values of all individuals. Then set the initial Pbest_value as the best value of groups gbest.
5.2. Updating speeds and locations
Population speed and location can be updated as expressions (26) and (27).
In which, r1,r2 are uniform random numbers within the range of [0,1].
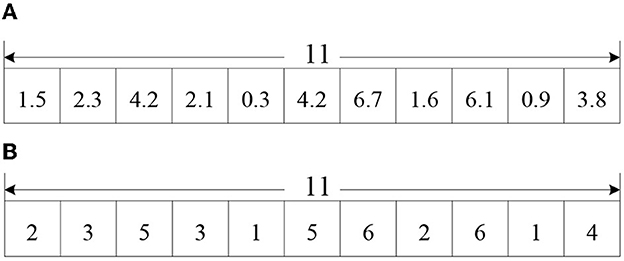
Traditional PSO is mainly used to solve the continuous optimization problem, while the model in this paper belongs to a discrete combinatorial problem. So, the updated particle positions and speeds need integer processing. Figure 4A is the result of an updating particle according to the particle update equations, and Figure 4B is the result of a particle rounds up to integers. Here, casualty group 5 and 10 are assigned to medical point 1, casualty group 1 and 8 are assigned to medical point 2, and so on.
5.3. Updating the best value of individuals
Comparing the current particle fitness value fitness with the individual historical optimal value Pbest_value, the smallest value is taken as the current individual optimal value Pbest_value, and its corresponding position is taken as the current individual optimal position Pbest.
5.4. Updating the best value of groups
Comparing the current individual optimal value Pbest_value with the group historical optimal value gbest_value, the smallest value is taken as the current group optimal value gbest_value, and its corresponding position is taken as the current group global optimal position gbest.
5.5. Termination of the algorithm
Determining whether the algorithm reaches the maximum iteration, if so, the algorithm terminates and outputs the optimal solution. Otherwise, go to step 4.2 and continue the iteration.
6. Computational experiments
6.1. Case description and data
The data of emergency medical rescue for Ya'an, in the Lushan earthquake, Sichuan province of China is used for numerical simulation. Taking town or township as units, Lushan County has jurisdiction over 5 towns and 4 townships. So, 9 affected points are set in this article. The nominal number of casualties in each affected point is shown in Supplementary Table S1. The number of treatment resources required by casualties with injury state r and g is 3 units and 2 units respectively.
Data shows that the Chinese government and military deployed 15 helicopters to transport and rescue casualties in the Lushan earthquake. Therefore, the number of available helicopters in medical points is set as 15. According to the basic Standard for Medical Institutions (Trial) issued by the Chinese Ministry of Health, there is one ambulance for every 50,000 people in the city. The number of ambulances in Ya'an city and Chengdu city is about 30 and 300, respectively. In this paper, it is assumed that 50% of ambulances in Ya'an city can be used normally, and due to the time crunch, only 50% of ambulances from nearby Chengdu city are used for the transport of casualties. So, the total number of available ambulances in this paper is set as 165. The other parameters to the model are set as following. Cr = 3 units, Cg = 2 units, vh = 40 km/h, vn = 120 km/h, qh = 2 persons, qn = 4 persons, T = 30 h. The number of medical resource limitations for each medical point is shown in Supplementary Table S2. The distance between medical points and affected points is shown in Supplementary Table S3.
Referring to literature (46), four failure scenarios are set in Supplementary Table S4. The failure scenarios are set as follows. No medical point failure in scenario 1, medical point 2 failure in scenario 2, medical point 4 failure in scenario 3, medical point 7 failure in scenario 4. 0 means the medical point failure in Supplementary Table S4. Supplementary Table S5 shows the degree of route damage εij.
6.2. Calculation results
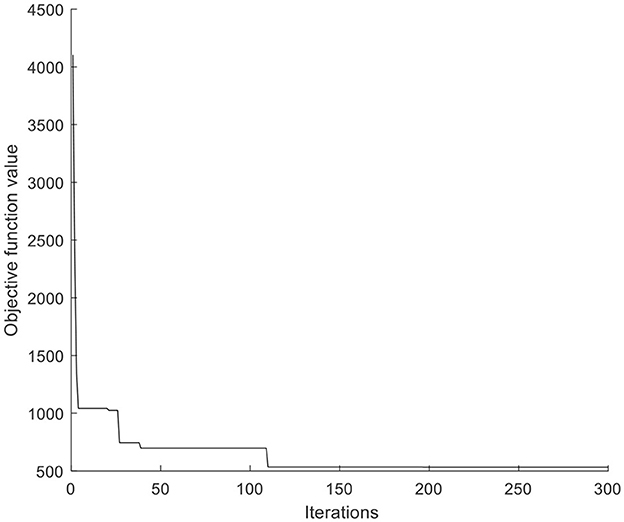
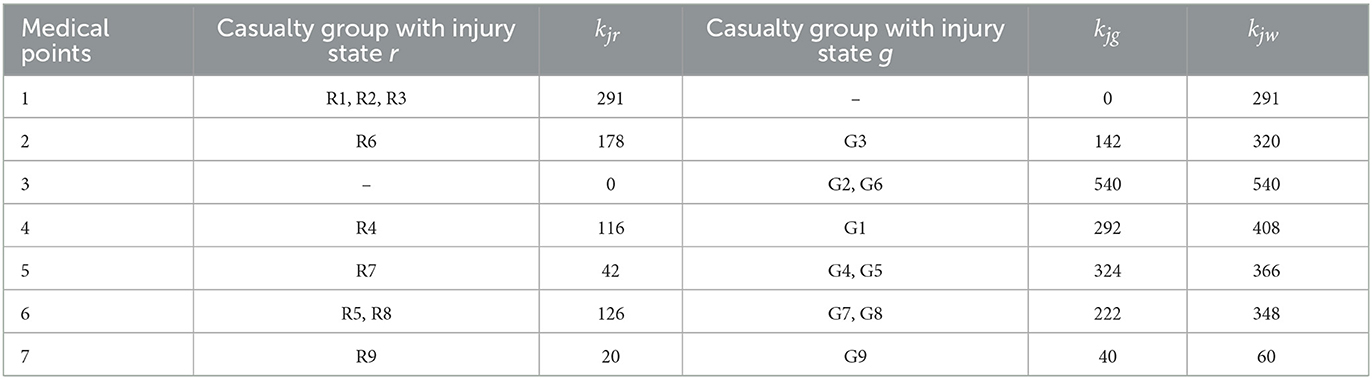
The PSO parameters are set as follows. Population size popsize = 100, learning factors c1 = c2 = 2, inertia weight w= 1, the maximum iterations maxgen = 300. MATLAB R2018b is used for programming, and it runs on a notebook computer with Intel(R) Core (TM) I5-5200U CPU and 12G memory. The optimal solution of the results of 10 operations is taken as the final solution. The convergence time of the algorithm is 10.171 s, and the objective function is 531.629. The convergence diagram of the algorithm is shown in Figure 5. Table 2 and Supplementary Table S6 are treatment information at medical points and affected points respectively.
6.3. Considering failures vs. without considering failures
To test the reliability of the scheme got by considering the point-edge mixed failures, a comparison was made between two schemes. Scheme 1 is the current optimization results got by considering the point-edge mixed failures. Scheme 2 is the results got without considering the failures. It is noted that the original objective function value in scheme 2 contains no factors of failures. The objective function value under each scenario in scheme 2 should be recalculated considering the facility failures and road disruption again (Table 3).
The results show that when there is no failure (scenario 1), the casualty scheduling results under scheme 1 are slightly worse than those under scheme 2. However, when the failure occurs after the earthquake, the solution result considering the failures is better than that without considering the failures. As shown in scenario 3, the total expected death probability of casualties under scheme 2 was 60.22% higher than scheme 1. Therefore, considering the point-edge mixed failure in advance can make more casualties receive timely treatment and reduce the death rate. The reliability of the system can be improved by considering the failures in the design stage of the emergency rescue network.
6.4. Robust optimization vs. deterministic optimization
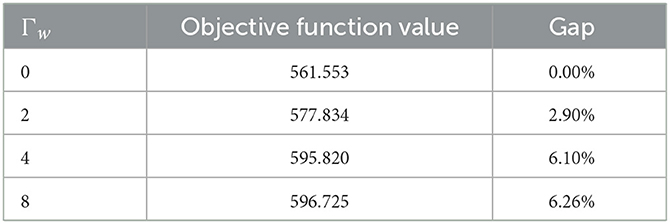
To verify the effectiveness of the robust optimization model, the running results of the robust optimization model and the deterministic model were compared in the same scenario. Four numerical examples are designed according to different control coefficients Γw, and the maximum disturbance value of casualty number deviating from the nominal value is 20%, that is . Table 4 shows the sensitivity analysis results of different robust control coefficients Γw. In general, although the objective function value of the robust optimization model is higher than that of the deterministic model, the gap is not significant. It shows that the robust optimization model can reduce uncertain risk. From the results of sensitivity analysis of Γw, the smaller the Γw, the stronger the robustness of the model. With the increase of the uncertainty of casualty numbers, the objective function value increases. The gap between the robust optimization model and the deterministic model (when Γw is 0) is gradually increasing. The appropriate scheme should be chosen according to the uncertain situation in practical decision-making.
6.5. Algorithm performance analysis
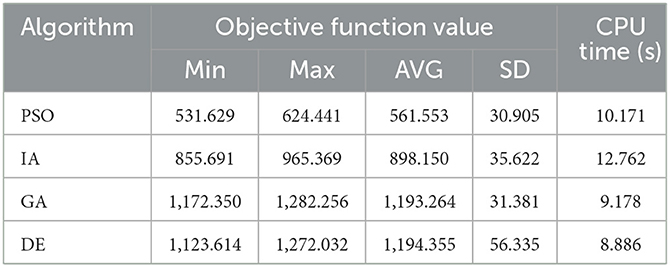
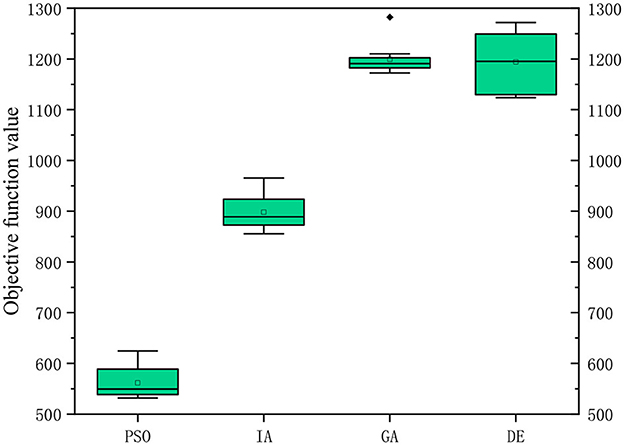
To test the performance of PSO, the algorithm was compared with GA, IA and DE. Each algorithm was run 10 times. The results are shown in Table 5 that the PSO is significantly superior to other algorithms. The average objective function value calculated by PSO reduces by 53.2% compared with GA, 37.5% compared with IA, and 53.0% compared with DE. The computational accuracy of PSO is better than GA, IA and DE, as shown in Figure 6.
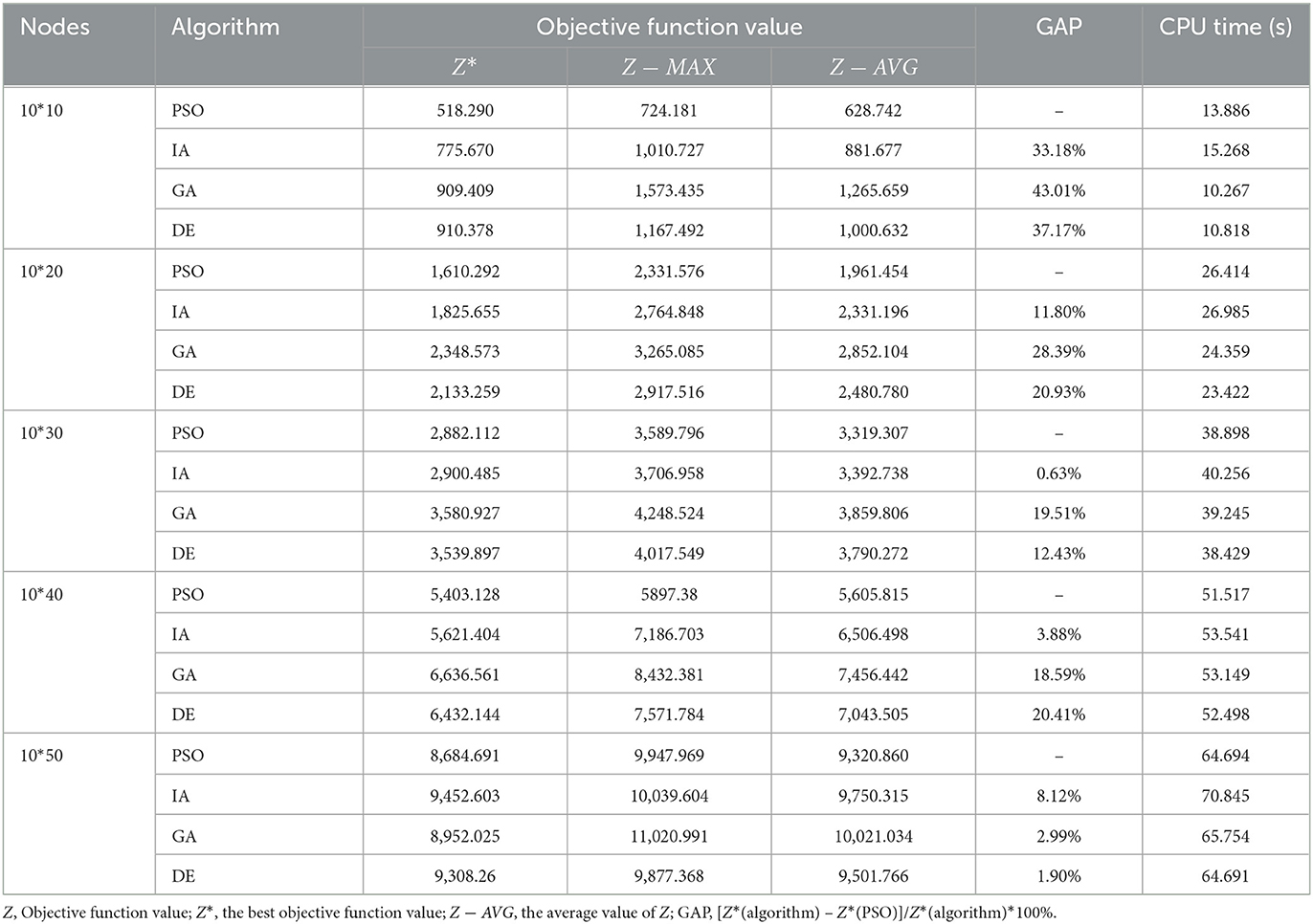
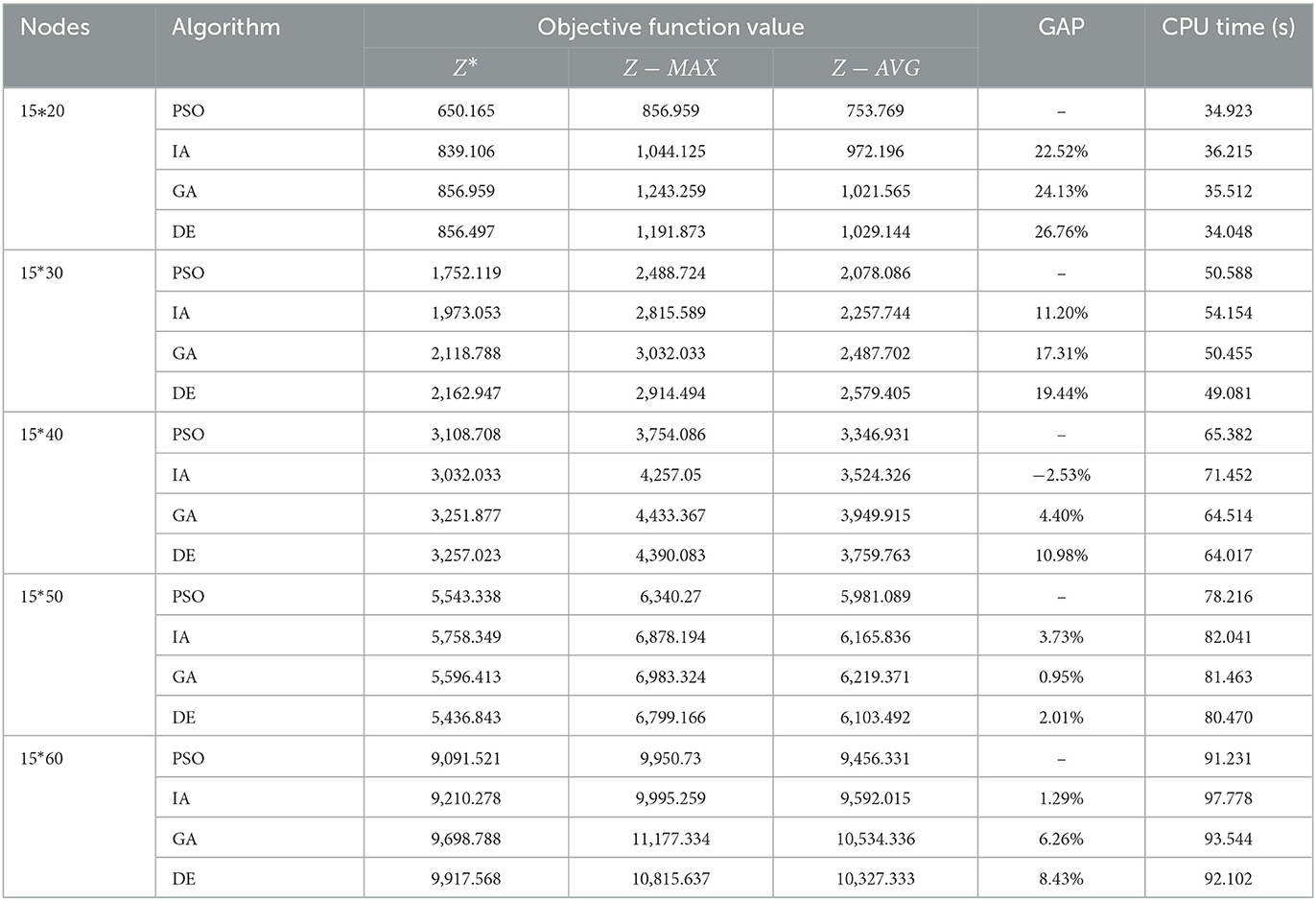
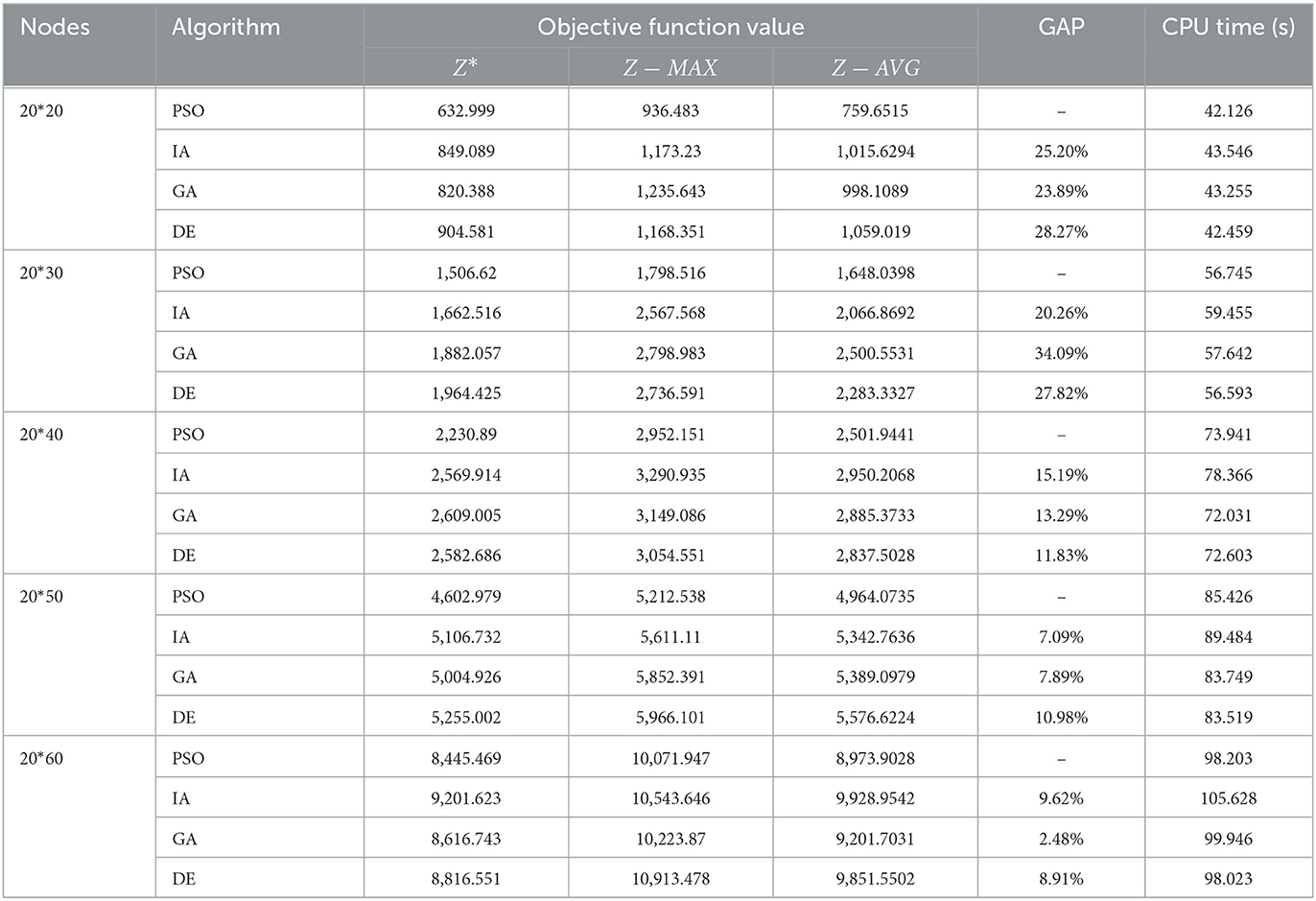
To further test the performance of the algorithm, three groups of examples are set for scale analysis. Each group contains five examples. The three groups have 10, 15 and 20 candidate medical points respectively. The calculation results are shown in Tables 6–8, and the box diagrams of the four algorithms for the three groups are shown in Figures 7A–C. The results show that PSO is better than GA, IA and DE obviously in terms of calculation accuracy. Among the 10 examples, only one example IA is better than PSO. The computational accuracy of PSO is better than GA, IA and DE for most examples. Therefore, the PSO designed in this paper can increase the optimization ability of the algorithm and has a good performance.
7. Conclusions
A robust optimization model was established in this paper to minimize the total expected death probability of casualties in the early stage of emergency rescue after an earthquake, considering the characteristics such as casualty classification, injury deterioration, point-edge mixed failures, medical resource limitation, and casualty number uncertainty. An improved PSO is proposed to solve the problem. Numerical experiments are conducted to verify the effectiveness of the model and algorithm under the context of the Lushan earthquake in China.
The results reveal that the operation effect of the emergency rescue network is significantly improved, and the optimization results are more reliable if the failure scenario is considered in advance. Moreover, robust optimization considering the casualty uncertainty can reduce the uncertainty risk of the system. Therefore, it is necessary to consider the point-edge mixed failures and casualty uncertainty simultaneously in the design stage of the emergency rescue network to establish a more reliable emergency rescue network.
Future research can consider the characteristics of the later stage of post-earthquake rescue comprehensively to study the casualty scheduling problem in the post-earthquake emergency recovery period while considering factors such as resuming normal passage of affected points and transporting the injured.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
YZ: writing and funding acquisition. YG: modeling and methodology. XH: data, algorithm, and computation. All authors contributed to the article and approved the submitted version.
Funding
This research is supported by the Chongqing Social Science Planning Project (No. 2021NDYB070), the Ministry of Education of Humanities and Social Science Project of China (No. 21YJCZH249), Natural Science Foundation of Chongqing Municipality (No. cstc2021jcyj-msxmX0527&cstc2021ycjh-bgzxm0136), Science and Technology Research Projects of Chongqing Education Commission (No. KJQN201900812), Humanities and Social Sciences Research Program of Chongqing Education Commission (No. 22SKGH186), and Innovative Research Project for Graduate Students of Chongqing Technology and Business University (No. yjscxx2022-112-24).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpubh.2023.995829/full#supplementary-material
References
1. Noham R, Tzur M. Designing humanitarian supply chains by incorporating actual post-disaster decisions. Eur J Oper Res. (2018) 265:1064–77. doi: 10.1016/j.ejor.2017.08.042
2. Bronfman A, Beneventti GD, Alvarez PP, Reid S, Paredes-Belmar G. The casualty stabilization-transportation problem in a large-scale disaster. Sustainability. (2022) 14:621. doi: 10.3390/su14020621
3. Liu C, Kou G, Peng Y, Alsaadi FE. Location-routing problem for relief distribution in the early post-earthquake stage from the perspective of fairness. Sustainability. (2019) 11:3420. doi: 10.3390/su11123420
4. Zhou Y, Zheng B, Su J, Li Y. The joint location-transportation model based on grey bi-level programming for early post-earthquake relief. J Indus Manag Optim. (2022) 18:45. doi: 10.3934/jimo.2020142
5. Haghani A, Jung S. A dynamic vehicle routing problem with time-dependent travel times. Comput Oper Res. (2005) 32:11. doi: 10.1016/j.cor.2004.04.013
6. Knightn VA, Harper P R, Smith L. Ambulance allocation for maximal survival with heterogeneous outcome measures. Omega. (2012) 40:918–26. doi: 10.1016/j.omega.2012.02.003
7. Coppi A, Detti P, Raffaelli J. A planning and routing model for patient transportation in health care. Electron Notes Discrete Math. (2013) 41:125–32. doi: 10.1016/j.endm.2013.05.084
8. Nayeri S, Tavakkoli-Moghaddam R, Sazvar Z, Heydari J. A heuristic-based simulated annealing algorithm for the scheduling of relief teams in natural disasters. Soft Comput. (2022) 26:1825–43. doi: 10.1007/s00500-021-06425-6
9. Mills AF, Argon NT, Ziya S. Resource-based patient prioritization in mass-casualty incidents. Manuf Serv Oper Manag. (2013) 15:361–77. doi: 10.1287/msom.1120.0426
10. Jotshi A, Gong Q, Batta R. Dispatching and routing of emergency vehicles in disaster mitigation using data fusion. Socioecon Plann Sci. (2009) 43:1–24. doi: 10.1016/j.seps.2008.02.005
11. Jin S, Jeong S, Kim J, Kim K. A logistics model for the transport of disaster victims with various injuries and survival probabilities. Ann Oper Res. (2015) 230:17–33. doi: 10.1007/s10479-013-1515-0
12. Gu J, Zhou Y, Das A, Moon I, Lee GM. Medical relief shelter location problem with patient severity under a limited relief budget. Comput Indus Eng. (2018) 125:720–8. doi: 10.1016/j.cie.2018.03.027
13. Mills AF, Argon NT, Ziya, S. Dynamic distribution of patients to medical facilities in the aftermath of a disaster. Oper Res. (2018) 66:716–32. doi: 10.1287/opre.2017.1695
14. Zhu L, Gong Y, Xu Y, Gu J. Emergency relief routing models for injured victims considering equity and priority. Ann Oper Res. (2019) 283:1573–606. doi: 10.1007/s10479-018-3089-3
15. Mansoori S, Bozorgi-Amiri A, Pishvaee MS. A robust multi-objective humanitarian relief chain network design for earthquake response, with evacuation assumption under uncertainties. Neural Comput Appl. (2020) 32:2183–203. doi: 10.1007/s00521-019-04193-x
16. Sun H, Wang Y, Xue Y. A bi-objective robust optimization model for disaster response planning under uncertainties. Comput Ind Eng. (2021) 155:107213. doi: 10.1016/j.cie.2021.107213
17. Chou CC, Chiang WC, Chen AY. Emergency medical response in mass casualty incidents considering the traffic congestions in proximity on-site and hospital delays. Transp Res Part E Logist Transp Rev. (2022) 158:102591. doi: 10.1016/j.tre.2021.102591
18. Caunhye AM, Nie X. A stochastic programming model for casualty response planning during catastrophic health events. Transp Sci. (2018) 52:437–53. doi: 10.1287/trsc.2017.0777
19. Ghasemi P, Khalili-Damghani K, Hafezalkotob A, Raissi S. Stochastic optimization model for distribution and evacuation planning (a case study of Tehran earthquake). Socio-Econ Plan Sci. (2020) 71:100745. doi: 10.1016/j.seps.2019.100745
20. Caglayan N, Satoglu SI. Multi-objective two-stage stochastic programming model for a proposed casualty transportation system in large-scale disasters: a case study. Mathematics. (2021) 9:316. doi: 10.3390/math9040316
21. Vahdani B, Veysmoradi D, Mousavi SM, Amiri M. Planning for relief distribution, victim evacuation, redistricting and service sharing under uncertainty. Socioecon Plann Sci. (2022) 80:101158. doi: 10.1016/j.seps.2021.101158
22. Zeng S, Weng S, Ye C. Multi-objective scheduling of wounded rescue vehicle for multi-center collaborative rescue after earthquake. J Control Engl Appl Inform. (2022) 24:24–34.
23. Cheng C, Adulyasak Y, Rousseau LM. Robust facility location under demand uncertainty and facility disruptions. Omega. (2019) 103:1–24. doi: 10.1016/j.omega.2021.102429
24. Sun H, Li J, Wang T, Xue Y. A novel scenario-based robust bi-objective optimization model for humanitarian logistics network under risk of disruptions. Transp Res E Log Transp Rev. (2022) 157:102578. doi: 10.1016/j.tre.2021.102578
25. Desi-Nezhad Z, Sabouhi F, Dehghani Sadrabadi MH. An optimization approach for disaster relief network design under uncertainty and disruption with sustainability considerations. RAIRO Oper Res. (2022) 56:2022021. doi: 10.1051/ro/2022021
26. Fiedrich F, Gehbauer F, Rickers U. Optimized resource allocation for emergency response after earthquake disasters. Saf Sci. (2000) 35:41–57. doi: 10.1016/S0925-7535(00)00021-7
27. Andersson T, Värbrand P. Decision support tools for ambulance dispatch and relocation. J Oper Res Soc. (2007) 58:195–201. doi: 10.1057/palgrave.jors.2602174
28. Xie C, Turnquist MA. Lane-based evacuation network optimization: An integrated Lagrangian relaxation and tabu search approach. Transp Res Part C Emerg Technol. (2011) 19:40–63. doi: 10.1016/j.trc.2010.03.007
29. Mclay LA, Mayorga ME. A model for optimally dispatching ambulances to emergency ALLS with classification errors in patient priorities. IIE Trans. (2013) 45:1–24. doi: 10.1080/0740817X.2012.665200
30. Knyazkov K, Derevitsky I, Mednikov L, Yakovlev A. Evaluation of dynamic ambulance routing for the transportation of patients with acute coronary syndrome in Saint-Pe-tersburg. Proc Comput Sci. (2015) 66:419–28. doi: 10.1016/j.procs.2015.11.048
31. Sung I, Lee T. Optimal allocation of emergency medical resources in a mass casualty incident: Patient prioritization by column generation. Eur J Oper Res. (2016) 252:623–34. doi: 10.1016/j.ejor.2016.01.028
32. Repoussis PP, Paraskevopoulos DC, Vazacopoulos A, Hupert N. Optimizing emergency preparedness and resource utilization in mass-casualty incidents. Eur J Oper Res. (2016) 255: 531–44. doi: 10.1016/j.ejor.2016.05.047
33. Shavarani SM, Vizvari B. Post-disaster transportation of seriously injured people to hospitals. J Human Logist Supply Chain Manage. (2018) 8:227–51. doi: 10.1108/JHLSCM-12-2017-0068
34. Caunhye AM, Li M, Nie X. A location-allocation model for casualty response planning during catastrophic radiological incidents. Socioecon Plann Sci. (2015) 50:32–44. doi: 10.1016/j.seps.2015.02.001
35. Salman FS, Gül S. Deployment of field hospitals in mass casualty incidents. Comput Indus Eng. (2014) 74:37–51. doi: 10.1016/j.cie.2014.04.020
36. Sheu J B, Pan C. A method for designing centralized emergency supply network to respond to large-scale natural disasters. Transp Res B. (2014) 67:284–305. doi: 10.1016/j.trb.2014.05.011
37. Hu Q-M, Zhao L, Li H, Huang R. Integrated design of emergency shelter and medical networks considering diurnal population shifts in urban areas. IISE Trans. (2019) 51:614–37. doi: 10.1080/24725854.2018.1519744
38. Na HS, Banerjee A. A disaster evacuation network model for transporting multiple priority evacuees. IIE Trans. (2015) 47:1287–99. doi: 10.1080/0740817X.2015.1040929
39. Talarico L, Meisel F, Sorensen K. Ambulance routing for disaster response with patient groups. Comput Oper Res. (2014) 56:120–33. doi: 10.1016/j.cor.2014.11.006
40. Rezapour S, Naderi N, Morshedlou N, Rezapourbehnagh S. Optimal deployment of emergency resources in sudden onset disasters. Int J Prod Econ. (2018) 204:365–82. doi: 10.1016/j.ijpe.2018.08.014
41. Feng Y, Liu T, Hu Z, Wang D, Cheng TCE, Yin Y. Casualty transport scheduling considering survival probability and injury classification. Comput Indus Eng. (2021) 161:107655. doi: 10.1016/j.cie.2021.107655
42. Lotfi MM, Baghaian A. Dynamic allocation strategies for medical teams in the first hours after mass casualty incidents. Adv Indus Eng. (2022) 56:43–55. doi: 10.22059/aie.2022.337140.1820
43. Wilson DT, Hawe GI, Coates G, Crouch RS. A multi-objective combinatorial model of casualty processing in major incident response. Eur J Oper Res. (2013) 230:643–55. doi: 10.1016/j.ejor.2013.04.040
44. Liu Y, Cui N, Zhang J. Integrated temporary facility location and casualty allocation planning for post-disaster humanitarian medical service. Transp Res E Logist Transp Rev. (2019) 128:1–16. doi: 10.1016/j.tre.2019.05.008
45. Bayram V, Yaman H. Shelter location and evacuation route assignment under uncertainty: a benders decomposition approach. Transp Sci. (2017) 52:416–36. doi: 10.1287/trsc.2017.0762
46. Zhou Y, Chen N, Li Z, Gong Y. Optimization design of emergency logistics network considering facility disruption scenarios during the early stage of post-earthquake relief. Oper Res Manage Sci. (2020) 29:107–12 (in Chinese). Available online at: https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C44YLTlOAiTRKibYlV5Vjs7i8oRR1PAr7RxjuAJk4dHXoopEuk-KPk0OA4odL6orxfiFzxSpQ2sH_cqCTeP9cICd&uniplatform=NZKPT
47. Mohammadi S, Avakh Darestani S, Vahdani B, Alinezhad A. A robust neutrosophic fuzzy-based approach to integrate reliable facility location and routing decisions for disaster relief under fairness and aftershocks concerns. Comput Ind Eng. (2020) 148:106734. doi: 10.1016/j.cie.2020.106734
48. Sabouhi F, Bozorgi-Amiri A, Vaez P. Stochastic optimization for transportation planning in disaster relief under disruption and uncertainty. Kybernetes. (2021) 50:2632–50. doi: 10.1108/K-10-2020-0632
49. Gong Y, Hu X, Zhou Y, Liu C. Robust optimization of casualty scheduling in the initial stage post-earthquake with road disruption and injury deterioration. Indus Eng Manage. (2022) 2022:1–17 (in Chinese).
50. Xu S. Study on Location-Routing Problem of Emergency Logistics Under Distribution Center Disruptions. Liaoning: Dalian Maritime University (2020) (in Chinese).
51. Bertsimas D, Sim M. The price of robustness. Oper Res. (2004) 52:35–53. doi: 10.1287/opre.1030.0065
52. Sun H, Xiang M, Xue Y. Robust optimization for emergency location-routing problem with uncertainty. Syst Eng Theory Methodol Appl. (2019) 28:1126–33 (in Chinese). Available online at: https://kns.cnki.net/kcms2/article/abstract?v=LP6_FsDEj27Np0Wig-h4b_dT5wXwYE5POeBLiFWGAY-Yh1l8UP8cPycGOtDPMxI3b9WUvusnxzQeh4Qqk0NYLGL-lQnNt5Ee0d5weW6rNkzGGWb_WsqkyjkUvJb0sdtNJHrOiefyOzmwocV_t5qZHw==&uniplatform=NZKPT&language=CHS
Keywords: emergency logistics, the injury worsened, facility disruption, robust optimization, particle swarm optimization
Citation: Zhou Y, Gong Y and Hu X (2023) Robust optimization for casualty scheduling considering injury deterioration and point-edge mixed failures in early stage of post-earthquake relief. Front. Public Health 11:995829. doi: 10.3389/fpubh.2023.995829
Received: 16 July 2022; Accepted: 31 January 2023;
Published: 20 February 2023.
Edited by:
Stephen Waller, Uniformed Services University, United StatesReviewed by:
Arvind Dhaka, Manipal University Jaipur, IndiaChong Xu, Ministry of Emergency Management, China
Yaping Ren, Jinan University, China
Copyright © 2023 Zhou, Gong and Hu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yufeng Zhou,  xtuzyf@qq.com
xtuzyf@qq.com
 Yufeng Zhou
Yufeng Zhou Ying Gong
Ying Gong