Skip to main content

REVIEW article

Front. Phys., 14 May 2024
Sec. Fluid Dynamics
Volume 12 - 2024 | https://doi.org/10.3389/fphy.2024.1383537

Bubble mass transfer in fluids under gravity: a review of theoretical models and intensification technologies in industry

www.frontiersin.orgYiyi Ma1* www.frontiersin.orgLinjiang Guo1 www.frontiersin.orgYuanhao Xiao1 www.frontiersin.orgAnhua Ji2
  • 1Department of Civil Engineering, Zhejiang University, Hangzhou, China
  • 2Senchuan Co., Ltd., Hangzhou, China

Bubble mass transfer is a common phenomenon in industrial applications. In this paper, bubble dynamics in both still and turbulent flow were introduced first, followed by the mass transfer properties of a single bubble and bubble swarms. Then, bubble mass transfer models for different scenarios were summarized, including three classical models, extended models, eddy diffusion and whirlpool theoretical models, and semi- or empirical correlations. Finally, existing methods for mass transfer intensification in industries were reviewed. Despite extensive researches, the mechanism for bubble mass transfer has not been fully understood. Models are commonly limited to some specific conditions and the accuracy is limited, especially for bubble swarms and bubble mass transfer in turbulent and non-Newtonian fluids. Also, the mass transfer intensification methods have their own limitations. Additional exploration of knowledge on bubble mass transfer models and further improvement in mass transfer intensification technologies are still required in the future.

Introduction

Gas-liquid mass transfer is triggered when the gas concentration in the liquid phase is lower than the saturation threshold or when the partial pressure of the gas in the liquid phase is higher than that in the gas phase [1]. It occurs naturally with the presence of gas bubbles in the liquid, like river turbulence-induced aeration, and is also widely applied in multiphase reactors in industries such as bubble columns, aeration tanks, and bio-fermentation plants [2, 3]. As reported, about 25% of chemical engineering reactors are the gas–liquid type [4].

Based on the existing knowledge, the total resistance during a gas-liquid mass transfer process can be divided into the one in the liquid film and the other in the gas film. For gases difficult to dissolve in liquid, like oxygen and nitrogen, the liquid film resistance is dominant [5]. This is the focus of the current study, for which the total mass transfer coefficient basically equals that in the liquid film. The mass transfer coefficient in the liquid phase is commonly denoted as KL, and the gas-liquid mass transfer rate can be calculated as dM/dt = -KLA(Cs - C), where M = gas mass inside bubbles, t = time, A = bubble-liquid interfacial area, C = dissolved gas concentration in liquid, and Cs = equilibrium concentration under the local partial pressure of the gas in the liquid. The mass transfer coefficient is an index measuring mass transfer efficiency, and a large value corresponds to a high efficiency. The gas-liquid mass transfer can also be expressed by the volumetric mass transfer coefficient KLA. Over the past hundred years, the mechanism for gas-liquid mass transfer has been studied extensively. However, due to its complexity and the increasing diversity of mass transfer conditions, the understanding of gas-liquid mass transfer requires further improvement.

In this paper, bubble dynamics were first reviewed, including the effects of path instability, breakup, and coalescence on bubble mass transfer. Then the characteristics of mass transfer of a single bubble and bubble swarms were presented, individually. The bubble mass transfer in non-Newtonian fluids was discussed subsequently. Following that, the bubble mass transfer models based on different principles are summarized, including the three classical models, extended models, and others developed from eddy diffusion theory and whirlpool theory. Semi- or empirical correlations of bubble mass transfer coefficient with different dimensionless numbers were also reviewed. Additionally, the methods for enhancing bubble mass transfer applied in industries were reviewed, including equipment improvement and introduction of a second energy separation agent and mass separation agent. Finally, the remaining issues in mass transfer studies and applications were summarized, and the future research directions were discussed. The paper is organized following Figure 1.

Figure 1
www.frontiersin.org

Figure 1. Organization of the review.

Characteristics of bubble mass transfer

Bubble dynamics and mass transfer

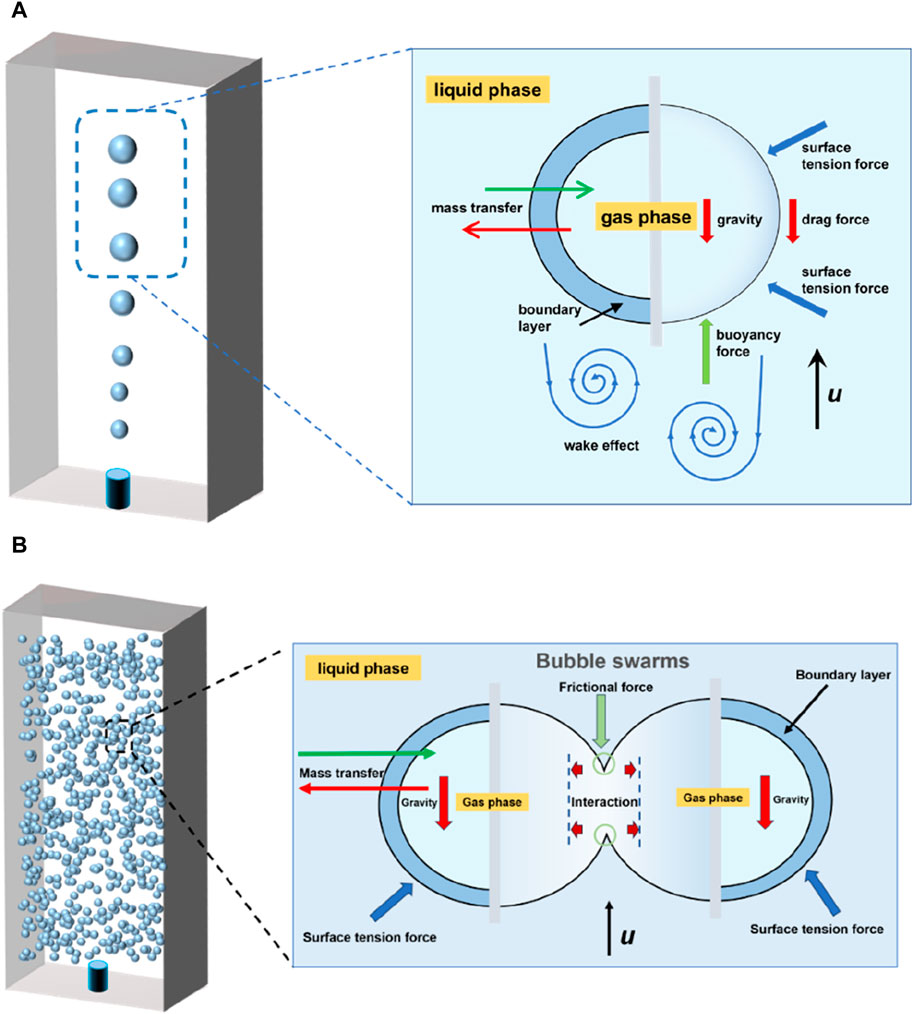
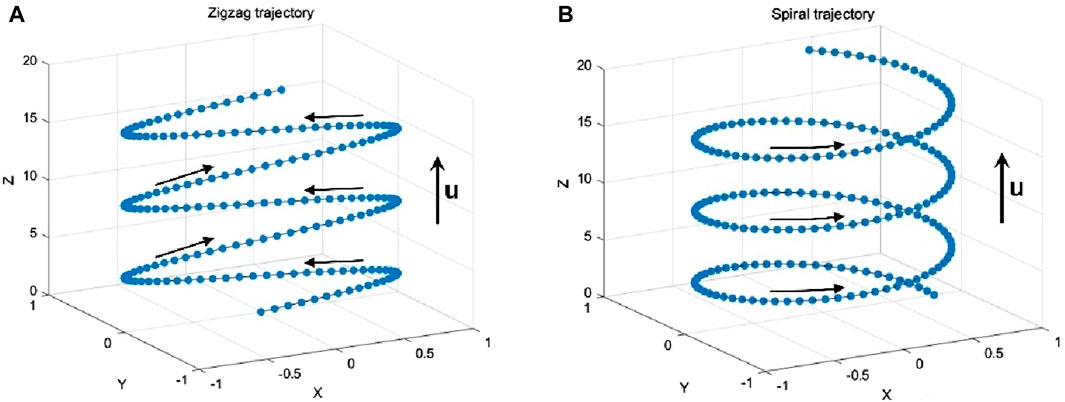
Bubble dynamics, mainly including path instability, breakup, and coalescence, are significantly related to the bubble mass transfer. When a bubble rises freely in still water, it is imposed by buoyancy force, drag force, and lift force, as shown in Figure 2A. Its path can switch to a zigzag or helical trajectory after traveling a straight vertical line, usually accompanied by significant bubble deformations and surface oscillation [6] (Figure 3). The path instability is caused by the symmetry breakage of the wake vortex behind the bubble [7, 8], which is governed by the bubble size [8].

Figure 2
www.frontiersin.org

Figure 2. Schematic of (A) a single bubble and (B) a bubble swarm moving upwards in still water.

Figure 3
www.frontiersin.org

Figure 3. (A) Zigzag and (B) spiral trajectories of a single bubble moving in still water.

There are extensive studies on the dynamics and mass transfer of a single bubble in still liquids, most focusing on the effects of bubble dynamics, bubble shape and trajectory, etc. Generally, the bubble path instability promotes convective transport and thereby strengthens mass transfer [9]. The interface oscillations induced during path instability also enhance the mass transfer near the interface [10]. The zigzag rising trajectory can accelerate the slippage of bubbles and reduce the thickness of the bubble concentration boundary layer, leading to enhanced local mass transfer [11]. The helical rising bubbles can generate an asymmetric wake with a lower terminal velocity than non-helical rising bubbles, and thus, leads to a less efficient mass transfer. The mass transfer coefficient in the bubble columns is also known to be dependent on the bubble dynamics. However, bubble swarms perform a different path instability from a single bubble, due to the turbulence induced among the moving bubbles (Figure 2B). As bubble swarms rise in liquid, bubbles coalescence or rebound frequently, which causes difficulty in determining their trajectories [12, 13].

The behaviors of bubble in turbulent flow are usually characterized by breakup and coalescence. Bubble breakup usually occurs under the effects of turbulent fluctuation and collision, viscous shear stress, shearing-off process, and interfacial instability [14].

Bubble coalescence is more complex than bubble breakup [4], which is not only affected by hydrodynamics, but also dependent on the effect of interfacial characterization. Bubble coalescence is caused by the relative bubble motions induced by the turbulence in the continuous phase, mean-velocity gradients, and buoyancy [15]. Large-size bubbles formed by coalescence exhibit a lower mass transfer efficiency [16]. When they break up into smaller bubbles, the mass transfer process is promoted. In addition, Tse et al. [17] found that, in some instances, the coalescence of two bubbles was accompanied by the formation of a much smaller daughter bubble generated by the annular wave following the breakup process. In coalescence-dominated systems, such processes can generate significant numbers of small bubbles [17]. Essentially, the path instability affects bubble diffusion and controls the local concentration in still water, while the coalescence and breakup of bubbles affect the size distribution of bubbles in turbulent flow [4]. Great turbulence caused by bubble swarm motion under the effect of buoyancy, can result in an enhanced mass transfer.

Most of the industrial reactors are operated under turbulent flow conditions. The dynamic behaviors of bubbles in turbulent flows are dramatically more complex than those in still water due to the random character of the turbulent fluctuations. The flow is not steady and the fluctuating conditions within turbulent flows can lead to deformation, breakup and self-sustained oscillations in the bubble [18]. Secondly, different from still water, there are regions of high vorticity and low-pressure vortices in turbulent flows [4]. The spatial structure of the velocity field around the bubble is unknown and depends on different eddies. For a single bubble in turbulent flow, the bubble mass transfer is strongly dependent on the Reynolds number and the Schmidt number [19]. The bubble Reynolds number based on the bubble slip velocity is used to reflect the bubble-liquid relative motion, and the liquid Reynolds number to characterize the turbulent intensity [20]. The relative velocity between bubble and liquid, and the liquid turbulence both have an important effect on the mass transfer. An increase in the liquid turbulence intensity contributes to the improvement of the surface renewal rate, and thus the enhancement of mass transfer [20].

Mass transfer characteristics of a single bubble in still water

The mass transfer of a single bubble in still water is the basis for understanding bubble mass transfer under complex conditions and in various gas-liquid reactors. The mass transfer of a single bubble in still water is a combination of molecular diffusion and convective transport [11]. For a single bubble, the mass transfer coefficient KL is mainly affected by bubble-liquid contact time, liquid viscosity and bubble equivalent diameter [21]. It decreases with the increase of the bubble-liquid contact time, probably due to the thickened bubble-liquid interface. The increase of liquid viscosity reduces the diffusion coefficient, and results in a lower mass transfer coefficient [22]. The bubble size has an essential effect on the mass transfer coefficient [23]. An increasing bubble equivalent diameter resulted in a decreasing bubble coalescence rate, a larger gas-liquid interface area, and a higher gas-liquid mass transfer coefficient. Smaller bubbles lead to less mass transfer due to small pulsations of turbulence around them. More specifically, for small bubbles with an equivalent diameter of 1–2 mm, the mass transfer coefficient is usually low, as the small bubbles have a rigid surface with negligible surface oscillations and internal circulation [24], which are essential to promote the gas-liquid mass transfer [25]. However, Hori et al. [26] found that, for spherical cap bubbles with an equivalent diameter greater than 5 mm, the mass transfer coefficient decreased with the increase of the equivalent diameter, due to the increasing flattening and aspect ratios of the bubble shape.

The bubble mass transfer is also dependent on the oscillation of the interface. As the size increases, bubbles become deformed and partially circulating. Bubble internal circulation increases with increasing size, and the shape oscillations occur at Re > 200 [11]. The oscillations of the bubble-liquid interface have been reported to improve the mass transfer [10, 27]. The reasons for the reduced mass transfer coefficient can also be the slippage at the bubble-liquid interface and the prevention of mass transfer resulting from the inert gases inside the bubble as well as the surfactants in the liquid phase [28]. For example, Bao et al. [11] reported that impurities (surface-active pollutants) in a contaminated system can influence the mobility of the bubble surface and increase the mass transfer resistance, which results in a smaller mass transfer coefficient than that in clean systems.

Mass transfer characteristics of bubble swarms

At large gas flow rates, bubbles in liquid become dense and the flow is featured with bubble swarms [29]. In practical industrial processes, gas-liquid mass transfer is usually in the form of bubble swarms, where the bubbles present various sizes, shapes and dynamics [30, 31]. Compared to a single bubble, the mass transfer characteristics of bubble swarms are more complex and the number of relevant studies has been much smaller. The mass transfer efficiency of bubble swarms is dependent on various parameters. First, the bubble size affects the gas exchange rate, bubble residence time, fluxes of volume and momentum, and thereby the mass transfer efficiency. Specifically, small bubbles have a high specific surface area, and can significantly improve the mass transfer from the gas phase to the liquid phase. Additionally, the large bubbles can induce considerable turbulence in the fluid, and promote mass transfer in the liquid [4]. According to Sahoo and Luketina [32], small bubbles with a radius of about 1 mm exhibited a higher oxygen transfer efficiency compared to larger bubbles.

Second, the way of bubble injection can affect the mass transfer efficiency. As reported by Gong et al. [33], concentrated injection of bubbles into liquid increased the bubble-induced liquid velocity, while it reduced the mass transfer efficiency. Uniform injection of bubbles performed higher mass transfer efficiencies than concentrated injection [33, 34]. The gas injection nozzle size also has an essential effect on mass transfer efficiency. For bubble swarms, the mass transfer rate increases with the decrease in the nozzle diameter [35]. Third, the size and height of the liquid container have an influence on the mass transfer efficiency of bubble swarms, and the effect also varies with the bubble size [36].

It has been widely accepted that the traditional single-bubble mass transfer theories cannot be applied directly to quantify the complex mass transfer processes of bubble swarms. For bubble swarms, the mass transfer performance is often empirically correlated with the volumetric mass transfer coefficient KLA [11]. The models for mass transfer of bubble swarms will be summarized in the subsequent sections.

Mass transfer of bubbles in non-Newtonian fluids

In non-Newtonian fluids, the mass transfer of bubbles is more complicated compared to that in Newtonian fluids. A non-Newtonian fluid has a varying viscosity with the change of shear rate. The viscosity variation of non-Newtonian liquid with shear rate varies with its rheological behavior. Non-Newtonian fluids can be further divided into Bingham fluids, pseudoplastic fluids and dilatant fluids [37]. Taking pseudoplastic fluids as an example, after a bubble being injected into the non-Newtonian fluid, the space expelled by the bubble movement does not recover immediately, which results in a vacuum behind the bubble. In a pseudoplastic fluid, restoring the vacuum region requires more energy than it does in a Newtonian fluid, thus slowing down the bubble movement. This causes a more significant drag coefficient of pseudoplastic fluids on the bubble than that of Newtonian fluids, and the bubble mass transfer coefficient is reduced as a result. However, some researchers found that, once the bubble size in non-Newtonian fluids is increased to a certain degree or the flow index reduced to a certain level, the wake effect, rise velocity and flow field turbulence can be enhanced, thereby increasing the mass transfer coefficient and improving the mass transfer efficiency [38]. The shape of bubbles can also be affected by non-Newtonian fluid. As reported by Bao et al. [11], the shape transition of bubbles in a pseudoplastic liquid is from ellipsoid to upside-down spherical cap, different from that in the Newtonian fluid (from ellipsoid to spherical cap).

The quantity and rheological properties of non-Newtonian material bring about the local acceleration or deceleration on slippage, shear rate, and thus irregular shape shifting and mass flux of gas–liquid interface. In addition, the gas–liquid mass transfer investigation in colored or non-transparent non-Newtonian fluids can be even more difficult, because the usual non-intrusive measurement methods can hardly be able to visual volume change or concentration distribution from these non-transparent fluids. Moreover, some non-Newtonian fluids, such as polyacrylamide solution, can exhibit both non-Newtonian behavior and surfactant-like effect, which may also decrease the mass transfer coefficient and increase the system complexity [39]. Therefore, the understanding of bubble mass transfer in non-Newtonian fluid is not as clear as that in Newtonian fluids.

Bubble mass transfer models

Classical models of gas-liquid mass transfer

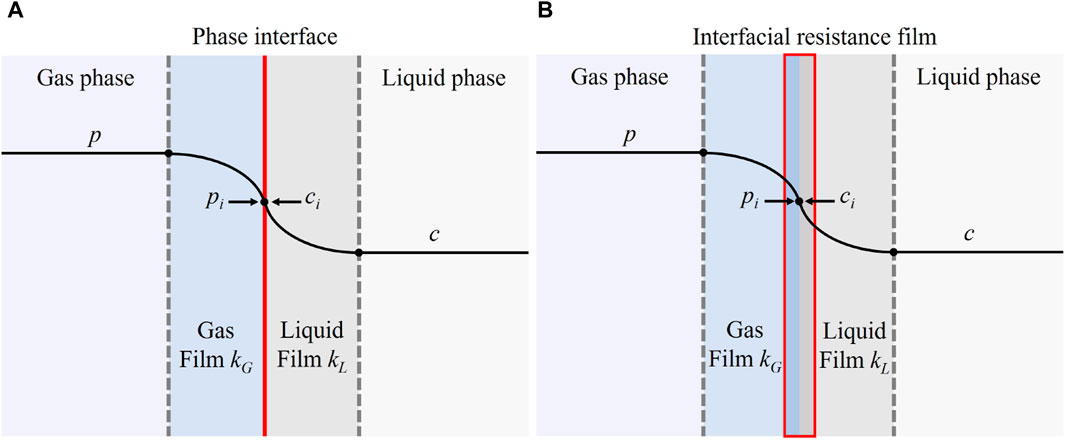
Researchers proposed various theoretical models and empirical correlations to predict the mass transfer coefficient. The most recognized models for gas-liquid mass transfer are the two-film model proposed by Whitman [40], the penetration model by Higbie [41] and the surface renewal model by Danckwerts [42]. The two-film theory assumes a stable liquid-gas interface with retardation films on both gas and liquid sides, with solute diffuses through the two films by molecular diffusion (Figure 4A). The two-film theory revealed the mechanism of gas-liquid mass transfer and laid a solid foundation for the subsequent studies. But it is only applicable when the Schmidt number (Sc = ν/D, ν = kinematic viscosity, D = diffusion coefficient) is small. Higbie [41] proposed the penetration theory, which assumes that the fluid is composed of elements, and the gas-liquid mass transfer is completed by the fluid elements. However, the penetration theory regards the residence time of the fluid elements at the gas-liquid interface as a constant, which is inconsistent with reality and difficult to obtain. As an improvement, the surface renewal model assumes that solute diffusion into the liquid phase is unsteady. Also, the residence time of fluid elements at the gas-liquid interface is considered varied, while the probability of elements being renewed is the same.

Figure 4
www.frontiersin.org

Figure 4. Schematic of (A) two-film model and (B) three-film model.

However, the actual mass transfer process is more complicated, and the assumptions made by the three models are inconsistent with reality to some extent. Additionally, some parameters in the models, like the surface renewal rate and the residence time of fluid elements, are difficult to measure, making the models challenging to be applied to practice. Despite the limitations, the three classical models provide a clear view of the mass transfer process and lay the foundation for studying the gas-liquid mass transfer mechanism.

Extended models from classical theories

Based on the three classical models, researchers have developed numerous models for mass transfer. For example, Ma and Yu [43] proposed the three-film theory of gas-liquid mass transfer based on the two-film theory, by considering three resistance films for gas-liquid mass transfer, namely, gas film, liquid film and interfacial resistance film (Figure 4B). The interfacial tension effect in the region near the gas-liquid interface was also included in the three-film theory, which caused a different molecules transportation mode compared to that in other regions. According to the three-film theory, the solute concentration close to the interfacial resistance film is

Ci=C∧e−ΔERT(1)

where ΔE = difference of interfacial energies between the two sides of the interfacial resistance film, T = temperature, and C∧ = equilibrium concentration. Perlmutter [44] improved the surface renewal model by considering the flow of fluid elements from the liquid bulk to the interface as a tandem process. In extreme cases, Perlmutter’s model can be converted into the classical models. That is, when there is only one fluid element for renewal, the model becomes the same as the classical surface renewal model, while it turns into the classical penetration model when the number of fluid elements in tandem approaches infinity. Shen et al. [21] proposed an improved surface renewal model by including the instability factors of surface film and the diffusion process in the film. In addition to the above models extended from one of the classical models, models developed by combining two or three of the classical models have also been reported. For example, Hanratty [25] proposed the film-penetration theory as a combination of the two-film theory and the penetration theory.

Models based on eddy diffusion theory and whirlpool theory

In addition to the three classical mass transfer models and those extended from them (e.g., Eq. 1), there are models established based on different theories like eddy diffusion theory and whirlpool theory. Eddy diffusion theoretical and whirlpool theoretical models consider the effects of the turbulence structure on mass transfer.

According to the similarity between mass transfer and momentum transfer, Levich [45] proposed an eddy diffusion model by assuming that the interphase mass transfer in semi-infinite space was mainly dominated by molecular diffusion and turbulent diffusion. Based on Levich’s model, King [46] reported that eddy flow dominated mass transfer enhancement in turbulence, where the large-scale eddies generated surface renewal, whereas the effect of those small ones can be damped by surface tension. He obtained the solute concentration distribution in the eddy by combing the eddy velocity equation and the convection-diffusion equation, and then calculated the eddy diffusion coefficient as

KL=a1nD1−1nfa2ntD2n−1,n(2)

where a and n are constants independent of t.

In the whirlpool models, the high-speed turbulent eddies near the interface are considered to play a leading role in mass transfer, and the mass transfer rate is greatly affected by the degree of turbulence. More specifically, the whirlpool models can be divided into large-scale eddies models (e.g., Fortescue and Pearson [47]), small-scale eddies models (e.g., Lamont and Scott [48]) and individual eddy models (e.g., Luk and Lee [49]). The large-scale eddies models consider that, in turbulent flows, among the energetic eddies with different scales near the interface, it is the large-scale energetic eddies controlling the gas-liquid mass transfer. The formula for the mass transfer coefficient is:

KL=1.46DUΛ(3)

where Λ = integral length from the interface and U = turbulent velocity near the interface. However, it is not easy to measure the eddy size distributions at the interface directly, which limits the practical application of the large eddy model.

The small eddy models consider that, although small-scale eddies contain lower energy, they can be fully mixed with adjacent large-scale energetic eddies, thereby transferring matter and energy among eddies of different scales, through motions including rotation, jetting, etc. Therefore, for the small eddy models, in a fully-developed turbulence field, the minimal viscous dissipative eddies control the mass transfer process. Lamont and Scott [48] developed the equation for the mass transfer coefficient by describing eddy velocities based on Kolmogorov’s eddy theory:

KL=A2D12εν−12(4)

where A2 = model constant determined from experimental data, and ε = turbulent kinetic energy dissipation rate.

Both the large and the small eddy models use the statistical averaging method to determine the eddy size and velocity, which poses difficulties in explaining the mass transfer mechanism of an individual eddy. In addition, whether large eddies or small eddies control the mass transfer process in the turbulence field is still debatable. Considering these concerns, Luk and Lee [49] proposed the individual eddy model, which was established based on a local equilibrium hypothesis. That is, although the mass transfer process across the interface was unsteady, the mass transfer within an individual eddy could be considered as stable. By assuming the flow velocity in an individual eddy as u, the component transport equation of the process is solved. Thus, the gas-liquid mass transfer coefficient of the model is obtained (Luk and Lee [49]):

KL=0.9DVL(5)

where V is the velocity fluctuation amplitude, and L is the velocity and length scale of an eddy. Compared with the large-scale eddy theory (e.g., Eq. 2 and 3) and the small-scale eddy theory (e.g., Eq. 4 and 5), the individual eddy theory further deepens the mass transfer mechanism to the level of single eddies.

Semi- or empirical correlations for bubble mass transfer

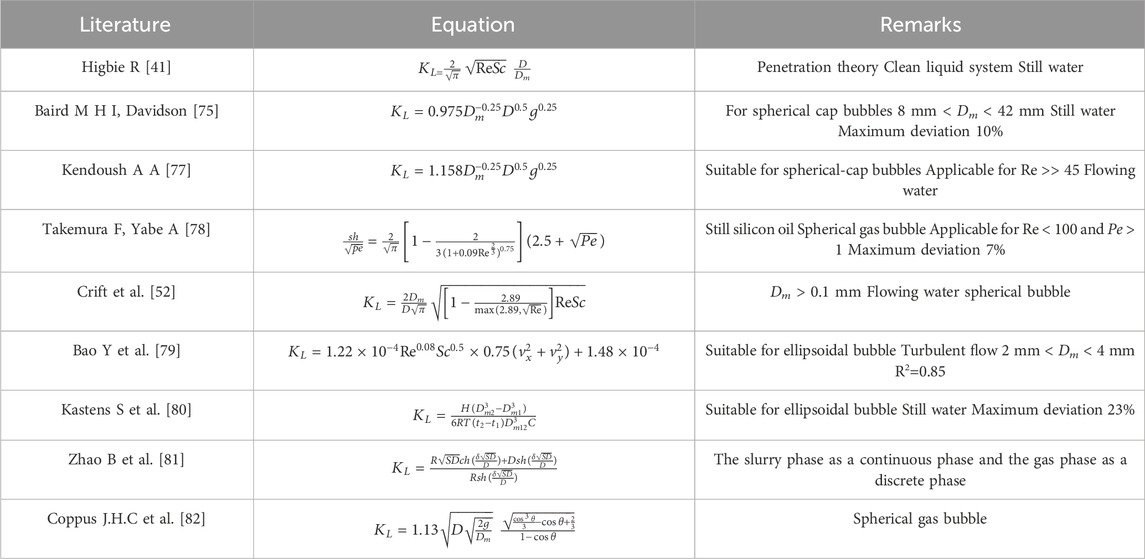
In addition to the models above, there have been extensive studies on KL, which has been reported to be a function of various factors, including gas diffusivity, liquid density and viscosity, gas-liquid affinity, as well as aeration and hydraulic conditions [50, 51]. Equations for calculating the mass transfer coefficients of a single bubble under different conditions have been widely reported, some as listed in Table 1. For example, Crift et al. [56] proposed an equation for the mass transfer coefficient of a spherical bubble as follows

KL=2π1−2.89max2.89,Re12Re12Sc12DDm(6)

where Re = Reynolds number (Re = ρvL/μ), and Dm = bubble diameter. Kendoush [59] developed the equation for the Sherwood number of ellipsoidal bubbles by improving Crift’s equation (Eq. 6), with Z being the bubble radius function that changes with the bubble quadrant angle:

Sh=0.564ReSc∫0π1+2Z3θ⁡sin3⁡θZ3θdθ(7)

In Eq. (7), θ = quadrant of the bubble.

Table 1
www.frontiersin.org

Table 1. Equations for single-bubble mass transfer coefficient

Generally, the mass transfer models for a single bubble are unlikely to be extrapolated to bubble swarms directly. Although the mass transfer of bubble swarms is highly complex, several researchers have made efforts to establish models. Alves et al. [60] established a model of the average mass transfer coefficient for bubble swarms, by using averaged bubble size, gas holdup, specific interfacial area and bubble residence time in bubble swarms, as Eq. (8):

KL=1.13tmvsDDm+tR−tmcvsDmD23vl−16tR(8)

where tR = bubble residence time and tm = the time span where bubbles behave like mobile fluid particles. Bork et al. [61] proposed an equation for the Sherwood number and verified the accuracy of the model experimentally, as Eq. (9)

Sh=4πFDReScSr(9)

where FD = enhancement factor (FD = 2 for bubble swarms), Sr = Strouhal number (Sr=fdhvs where f is the bubble rise path and dh is the bubble diameter of the major axis). Additional representative models are listed in Table 2 for reference.

Table 2
www.frontiersin.org

Table 2. Equations for bubble swarm mass transfer coefficient

In non-Newtonian fluids, the mass transfer of bubbles is more challenging to compute than Newtonian fluids. Baird and Hamielec [65] developed an equation for the Sherwood number of a single-bubble mass transfer in Newtonian fluids, as Eq. (10)

Sh=2πPe∫0πvθvmaxsin2⁡θdθ(10)

where Pe = Peclet number defined as Pe=VLD, vθ = surface velocity, and vmax = velocity relative to continuous phase. Based on their equation, Hirose and Moo-Young [66] proposed a semi-empirical mass transfer formula for a single spherical bubble in non-Newtonian fluids, as Eq. (11)

Sh=0.65Pe1−4mm−12m+1(11)

Here, m = correction factor of non-Newtonian fluids. Kawase and Moo-Young [62] derived equations for the mass transfer coefficients of bubbles moving freely under gravity in non-Newtonian fluids based on the early work of Calderbank and Moo-Young, as Eq. (12)

KL=0.975DgDm14(12)

Note that the bubble mass transfer in colored or non-transparent non-Newtonian fluids can be even more challenging to investigate, because the usual non-intrusive measurement methods can hardly be able to visualize the volume change or concentration distribution in these non-transparent fluids [11]. Moreover, a few types of non-Newtonian fluids, e.g., polyacrylamide solution, can exhibit both non-Newtonian behavior and surfactant-like effect, which can decrease KL and cause additional complexity to the system [67]. Due to the difficulties, most existing models for mass transfer coefficient are developed by fitting the experimental data, which makes them only suitable for some specific working conditions and lack generality.

Limitations of existing bubble mass transfer models

Generally, the current understanding of the mass transfer mechanism is limited, and there is still a knowledge gap on bubble mass transfer predictions. For most theoretical models, the parameters are not easy to measure or link with operational conditions. Although extensive semi- or empirical correlations for bubble mass transfer coefficient have been reported, most are developed by fitting the experimental data and are only applicable under some specific conditions. As the bubble mass transfer proceeds under diverse conditions and the liquid-bubble interactions vary with equipment, it is still difficult to be unified as models. Additionally, there is a lack of a connection mechanism between the mass transfer of a single bubble and bubble swarms. Also, there are difficulties in measuring bubble mass transfer rate due to the challenge in bubble volume estimation caused by bubble shape-shifting, especially in turbulent flow, which limits model improvement.

Intensification of bubble mass transfer in industry

Intensification of mass transfer is beneficial to industrial processes in aspects of improving product quality, reducing cost, raising production efficiency, and safety. To enhance the efficiency of industrial production, a profound comprehension of the interdependence between bubble dynamic behaviors, mass transfer mechanisms, and hydrodynamics is imperative. For bubble swarms, large bubbles contribute to the formation of induced turbulence, thereby promoting convective mass transfer in the liquid phase, and small bubbles offer a higher specific surface area. Therefore, reasonable control of the size distribution in bubble swarms, and maintaining a proper hydraulic condition in the reactor can enhance gas–liquid mass transfer. Generally, the mass transfer can be enhanced in the following ways: (1) to improve reactors by installing hydrodynamic optimization structures like baffles, (2) to introduce a second energy separation agent, such as electric field, acoustic field, and magnetic field, (3) to introduce mass separation agents, like micron-sized particles, nano-sized particles, etc. The ways of mass transfer enhancement are presented in detail in the following.

Installing hydrodynamic optimization structures

One of the common intensifications of mass transfer in bubble columns is to construct horizontal or vertical baffles in the reaction chamber, which changes flow direction and enhances turbulence, thereby improving mass transfer. Yin et al. [68] constructed rectangular baffles with staggered arrangement in the channel to improve the gas-liquid mass transfer efficiency of the CO2-water system. With baffles, the highest bubble mass transfer coefficient reached 2.8 times the coefficient without baffles. The mass transfer is enhanced by the strengthened turbulence in the liquid phase due to the baffle disturbance, which causes bubble breakup and promotes surface renewal. Gu et al. [69] proposed a new type of rotating packed bed to enhance turbulence in the gas phase. With such a rotating packed bed, the mass transfer coefficient was twice that of traditional designs. Another solution is to install stirrers or vibration exciters inside the reaction chamber of a bubble column to enhance circulation and, thereby mass transfer. However, this method is only effective in a narrow range of process parameters [70]. It can also cause undesirable hydraulic conditions in the bubble column, like back mixing and phase separation, which can reduce the mass transfer coefficient [70].

Introducing second energy separation agent

Introducing energy into mass transfer equipment is another essential means to enhance mass transfer, including stirring, oscillation, and adding energy fields (magnetic fields, sound fields, supergravity fields, etc.). For example, introducing pulsations inside a bubble column or subjecting the entire column to pulsations can cause bubble breakup and elimination of bubble rise, which increases the liquid-bubble interfacial area and the contact time, and thereby enhancing mass transfer [70]. Zou et al. [71] reported that stirring and aeration could weaken the phenomenon of concentration polarization and improve mass transfer efficiency significantly. Zhang et al. [72] found that solid particle oscillation enhanced the radial mixing of the fluid, and the mass transfer coefficient was increased by more than 50%. Reichert et al. [73] found that the use of external alternating magnetic fields along with suspended magnetic particles could lead to forced and highly intensive particle movement in liquid-gas mixture, which increased the mass transfer coefficient by up to 200%. However, the methods of stirring and oscillation are not suitable for traditional equipment such as bubble columns and packed columns. There are also limitations to introducing the energy field, e.g., electric and magnetic fields are only suitable for substances with a certain charge and magnetism. Also, the high cost of adding an energy field needs to be taken into consideration for industrial applications [74].

Introducing mass separation agent

Introducing mass separation agents, dispersed particles as the commonest, can significantly reduce the mass transfer resistance, and accelerate the mass transfer process [75]. Ferreira et al. [76, 77] experimentally studied the effects of adding expandable polystyrene (EPS) particles (hydrophobic) and hollow glass beads (hydrophilic) on the mass transfer in a bubble column. The results showed that the hydrophobic micron-sized EPS particles always harmed the mass transfer process. The effect of hydrophilic hollow glass beads was a function of the solid holdup, i.e., the mass transfer coefficient increased with an increasing solid holdup of up to 10% and decreased with further higher holdups. The fine particles promote surface renewal thus the mass transfer at lower solid holdups, when the change in liquid viscosity is negligible. However, when the solid holdup is over a certain level, the viscosity of the liquid phase increases, and the fine particles at the gas-liquid interface prevent the gas diffusion to the liquid phase. Thus, the mass transfer coefficient decreases.

With the development of nanotechnology in the last decades, nanoparticles have become a popular choice as a mass transfer promoter. Colloids composed of ultrafine nanoparticles (100 nm or smaller) are called nanofluids [77]. Olle et al. [78] experimentally investigated the effects of aqueous suspensions of 20–25 nm magnetic (Fe3O4) nanoparticles on the bubble mass transfer in an agitated and sparged reactor. Their results showed that, with nanoparticle volume fractions below 1%, the bubble mass transfer could be enhanced up to 600%. Park et al. [79] measured the chemical absorption rate of CO2 into an aqueous solution of nanometer-sized colloidal silica (0–31 wt%) and 2-amino-2-methyl-1-propanol in a stirred vessel. They found that the volumetric liquid-side mass transfer coefficient and the absorption rate in the nanofluid decreased as the nanoparticle concentration increased, which could be due to the increase of system viscosity.

There are still problems for using nanoparticles to enhance gas-liquid mass transfer in practice. Specifically, (1) the mass transfer effect of the same type of nanoparticles varies under different experimental conditions, which can be related to the nanoparticle properties, preparation methods and stability of nanofluids [69]; (2) the enhancement mechanism of nanoparticles on mass transfer is still unclear, which is simply attributed to the micro-convection caused by Brownian motion of the nanoparticles currently; (3) few devices are available to observe the movement of nanoparticles under ordinary solid content [80]; (4) due to the limitations of the stability and visualization of nanoparticles, the universality and accuracy of current calculation methods for mass transfer with nanoparticles still require improvement.

Application of microreactors

Microreactors featured with bubble mass transfer performing in micrometer-sized channels have also been reported as a way to enhance bubble mass transfer [81]. Due to the short diffusion path and huge specific surface area of bubble mass transfer in micrometer-sized channels, the volumetric mass transfer coefficient in microreactors can be one to three orders of magnitude higher than that in traditional gas-liquid reactors [82]. The structure of microchannel is closely related to the mass transfer efficiency. It is usually designed with convergent-divergent channels, bend, built-in obstacle, etc., to increase the gas-liquid interfacial area and enhance the flow disturbance, and thereby improving mass transfer efficiency. External energy was also introduced to disturb the flow, like ultrasound [83]. Many researchers have explored designs of microreactors for various purposes. For example, Ganapathy et al. (2016) [82] studied the mass transfer performance of a microreactor which was with 15 straight parallel channels of 456 μm diameter in a cross-flow inlet configuration. They found that the efficiencies of CO2 absorption into aqueous diethanolamine nearly reached 100% under certain operating conditions, which indicated the significant effect of mass transfer intensification of the microreactor. Yin et al. (2022) [81] proposed a split-and-recombine (SAR) microreactor, composed of convergent–divergent arc channel and rectangular obstacles. The bubble dynamic features and mass transfer characteristics were revealed, which showed that the SAR microreactor performing well in enhancing the gas–liquid mass transfer with rapid chemical reaction. Liu et al. (2023) reported a bubble-based microreactor (BBMR), and it also performed excellently in promoting the mass transfer process [84]. Nevertheless, there are still many technical barriers for microreactors, like commercialization and specific reaction integration problems. Also, critical analysis including synthesis ability, measurement analysis, extraction, and detection should be conducted before the microreactors being applied widely in industry[85, 86].

Conclusion and future aspects

In this review paper, characteristics of mass transfer of a single bubble and bubble swarms were presented. The effects of parameters on bubble mass transfer were reviewed, like gas-liquid contact time, liquid viscosity, bubble size, traveling trajectory, bubble injection conditions, etc. Following that, bubble mass transfer models for different conditions were summarized, including three classical models, extended models and those based on eddy diffusion and whirlpool theories. Semi- or empirical correlations of bubble mass transfer coefficient with different dimensionless numbers were also reviewed. Additionally, technologies for enhancing bubble mass transfer in industries were introduced, in aspects of equipment improvement and introduction of a second energy separation agent and mass separation agent.

Despite the extensive research, the mechanism for bubble mass transfer has not been fully understood, especially for bubble swarms and bubble mass transfer in turbulent and/or non-Newtonian fluid flows. Besides, the accuracy of mass transfer models still needs to be improved, especially for bubble swarms, due to their complex characteristics of heterogeneity, multi-scale, nonlinearity, unsteady state, etc. Most existing multi-bubble mass transfer models were developed based on the single-bubble mass transfer model, and the complex processes of bubble coalescence and breakup were commonly not considered. Currently, despite numerous measurement techniques proposed to capture the dynamic behavior of local bubbles, it remains challenging to obtain more micro and mesoscopic information in gas–liquid systems, in order to establish a comprehensive theory of bubble dynamics. For example, the flow field around the bubble affects mass transfer near the interface, and simultaneously, deforms the bubble interface, which changes the interfacial area, and in turn, leads to a time-dependent concentration gradient across the interface [87]. The existing technique has limitations in quantifying such a mass transfer process.

Based on the main influencing factors of the mass transfer coefficient, the enhancement of bubble mass transfer can be achieved by reducing gas-liquid contact time and obtaining proper bubble sizes. However, the traditional methods have their limitations, e.g., they are only suitable for some specific scenarios. Micro-nanobubbles and nanofluids have become emerging technologies to promote bubble mass transfer processes. But the relevant knowledge is not completed, and the existing nanoscale-enhanced gas-liquid mass transfer model most have a low prediction accuracy. Additional studies on bubble mass transfer models and a further improvement in mass transfer strengthening technologies are still required.

Based on the above summary, future research on bubble mass transfer can be carried out in the following fields: (1) to develop accurate measurements for flow field and bubble dynamics, as well as bubble mass transfer rate; (2) to further explore the application of micro-nanobubbles and nanofluids in enhancing mass transfer. Additionally, machine learning (ML) has been recognized as capable of identifying the correlation between experimental data on bubble dynamic behavior and mass transfer processes, thereby expediting the research process [88]. Machine learning is able to make predictions for the size, behavior, and mass transfer process of bubbles under different conditions. Therefore, to apply machine learning to bubble mass transfer study is also an important research direction in the future.

Author contributions

YM: Funding acquisition, Methodology, Supervision, Writing–original draft, Writing–review and editing. LG: Writing–original draft, Writing–review and editing. YX: Writing–original draft. AJ: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The writers gratefully acknowledge financial support from the Natural Science Foundation of Zhejiang Province (Grant No. LZJWZ23E090009), the Open Fund Research Project by the State Key Laboratory of Hydraulics and Mountain River Engineering (Sichuan University, No. SKHL2110), and the National Natural Science Foundation of China (Grant No. 52300122).

Conflict of interest

Author AJ was employed by Senchuan Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Cheng W, Liu W, Hu B, et al. Experimental study on gas-liquid two-phase flows in an aeration tank by using image treatment method. J Hydrodynamics, Ser. B (2008) 20(5):650–5.

CrossRef Full Text | Google Scholar

2. Kantarci N, Borak F, Ulgen KO. Bubble column reactors. Process Biochem (2005) 40(7):2263–83. doi:10.1002/chin.200531271

CrossRef Full Text | Google Scholar

3. Yang Z, Zhang Z, Yang , Lu JS. Oxygen gas-liquid mass transfer characteristics under the effect of enhanced ventilation in sewage pipes. Environ Sci (2022) 43(04):2055–61. doi:10.13227/j.hjkx.202107083

CrossRef Full Text | Google Scholar

4. Yan S, Wang X, Zhu L, Zhang X, Luo Z. Mechanisms and modeling of bubble dynamic behaviors and mass transfer under gravity: a review. Chem Eng Sci (2023) 277:118854. doi:10.1016/j.ces.2023.118854

CrossRef Full Text | Google Scholar

5. Saito T, Toriu M. Effects of a bubble and the surrounding liquid motions on the instantaneous mass transfer across the gas–liquid interface. Chem Eng J (2015) 265:164–75. doi:10.1016/j.cej.2014.12.039

CrossRef Full Text | Google Scholar

6. Cano-Lozano JC, Martinez-Bazan C, Magnaudet J, Tchoufag J. Paths and wakes of deformable nearly spheroidal rising bubbles close to the transition to path instability. Phys Rev Fluids (2016) 1(5):053604. doi:10.1103/physrevfluids.1.053604

CrossRef Full Text | Google Scholar

7. Liu H, Zhang Y, Wei Y, Mu Z, Yang Y, Farooq MS. Characteristics and mechanisms of the zigzag and spiral movement of rising bubbles in still water. Appl Sci (2023) 13(11):6500. doi:10.3390/app13116500

CrossRef Full Text | Google Scholar

8. Zenit R, Magnaudet J. Path instability of rising spheroidal air bubbles: a shape-controlled process. Phys Fluids (2008) 20(6). doi:10.1063/1.2940368

CrossRef Full Text | Google Scholar

9. Zhang B, Wang Z, Luo Y, Guo K, Zheng L, Liu C. A mathematical model for single CO2 bubble motion with mass transfer and surfactant adsorption/desorption in stagnant surfactant solutions. Separat Purif Technol (2023) 308:122888. doi:10.1016/j.seppur.2022.122888

CrossRef Full Text | Google Scholar

10. Xie Y, Chindam C, Nama N, Yang S, Lu M, Zhao Y, et al. Exploring bubble oscillation and mass transfer enhancement in acoustic-assisted liquid-liquid extraction with a microfluidic device. Scientific Rep (2015) 5(1):12572. doi:10.1038/srep12572

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Bao Y, Jia J, Tong S, Gao Z, Cai Z. A review on single bubble gas–liquid mass transfer. Chin J Chem Eng (2020) 28(11):2707–22. doi:10.1016/j.cjche.2020.07.037

CrossRef Full Text | Google Scholar

12. Sanada T, Sato A, Shirota M, Watanabe M. Motion and coalescence of a pair of bubbles rising side by side. Chem Eng Sci (2009) 64(11):2659–71. doi:10.1016/j.ces.2009.02.042

CrossRef Full Text | Google Scholar

13. Sanada T, Watanabe M, Fukano T. Effects of viscosity on coalescence of a bubble upon impact with a free surface. Chem Eng Sci (2005) 60(19):5372–84. doi:10.1016/j.ces.2005.04.077

CrossRef Full Text | Google Scholar

14. Liao Y, Lucas D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem Eng Sci (2009) 64(15):3389–406. doi:10.1016/j.ces.2009.04.026

CrossRef Full Text | Google Scholar

15. Kamp AM, Chesters AK, Colin C, Fabre J. Bubble coalescence in turbulent flows: a mechanistic model for turbulence-induced coalescence applied to microgravity bubbly pipe flow. Int J Multiphase Flow (2001) 27(8):1363–96. doi:10.1016/s0301-9322(01)00010-6

CrossRef Full Text | Google Scholar

16. Shen J, Wang L. Experimental study on the effect of interfacial mass transfer on coalescence of gas bubbles. Chin J Process Eng (2016) 16(02):204–9.

Google Scholar

17. Tse KL, Martin T, McFarlane CM, Nienow A. Small bubble formation via a coalescence dependent break-up mechanism. Chem Eng Sci (2003) 58(2):275–86. doi:10.1016/s0009-2509(02)00528-6

CrossRef Full Text | Google Scholar

18. Ravelet F, Colin C, Risso F. On the dynamics and breakup of a bubble rising in a turbulent flow. Phys Fluids (2011) 23(10). doi:10.1063/1.3648035

CrossRef Full Text | Google Scholar

19. Saboni A, Alexandrova S, Karsheva M, Gourdon C. Mass transfer into a spherical bubble. Chem Eng Sci (2016) 152:109–15. doi:10.1016/j.ces.2016.06.001

CrossRef Full Text | Google Scholar

20. Bao Y, Jiang Z, Tong S, Huang X, Cai Z, Gao Z. Reactive mass transfer of single O2 bubbles in a turbulent flow chamber. Chem Eng Sci (2019) 207:829–43. doi:10.1016/j.ces.2019.07.006

CrossRef Full Text | Google Scholar

21. Shen Z, Xu W, et al. Interphase mass transfer(I) a modified surface film renewal model. J Chem Industry Eng (China) (2020) 1980(04):319–32.

Google Scholar

22. Saboni A, Alexandrova S, Spasic AM, Gourdon C. Effect of the viscosity ratio on mass transfer from a fluid sphere at low to very high Peclet numbers. Chem Eng Sci (2007) 62(17):4742–50. doi:10.1016/j.ces.2007.05.021

CrossRef Full Text | Google Scholar

23. Chen P, Qing S, et al. Research progress on enhanced gas-liquid mass transfer by nanofluids. China Water Transport (Second Half Month) (2020) 20(09):82–3.

Google Scholar

24. Dani A, Guiraud P, Cockx A. Local measurement of oxygen transfer around a single bubble by planar laser-induced fluorescence. Chem Eng Sci (2007) 62(24):7245–52. doi:10.1016/j.ces.2007.08.047

CrossRef Full Text | Google Scholar

25. Hanratty TJ. Turbulent exchange of mass and momentum with a boundary. AIChE J (1956) 2(3):359–62. doi:10.1002/aic.690020313

CrossRef Full Text | Google Scholar

26. Hori Y, Hayashi K, Hosokawa S, Tomiyama A. Mass transfer from single carbon-dioxide bubbles in electrolyte aqueous solutions in vertical pipes. Int J Heat Mass Transfer (2017) 115:663–71. doi:10.1016/j.ijheatmasstransfer.2017.07.087

CrossRef Full Text | Google Scholar

27. Akbari M, Rahimi M, Faryadi M. Gas–liquid flow mass transfer in a T-shape microreactor stimulated with 1.7 MHz ultrasound waves. Chin J Chem Eng (2017) 25(9):1143–52. doi:10.1016/j.cjche.2017.03.010

CrossRef Full Text | Google Scholar

28. Vasconcelos JMT, Orvalho SP, Alves SS. Gas–liquid mass transfer to single bubbles: effect of surface contamination. AIChE J (2002) 48(6):1145–54. doi:10.1002/aic.690480603

CrossRef Full Text | Google Scholar

29. Liu L, Zhang H, Yan H, Ziegenhein T, Hessenkemper H, Zhou P, et al. Experimental studies on bubble aspect ratio and corresponding correlations under bubble swarm condition. Chem Eng Sci (2021) 236:116551. doi:10.1016/j.ces.2021.116551

CrossRef Full Text | Google Scholar

30. Riboux G, Risso F, Legendre D. Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J Fluid Mech (2010) 643:509–39. doi:10.1017/s0022112009992084

CrossRef Full Text | Google Scholar

31. Colombet D, Legendre D, Cockx A, Guiraud P, Risso F, Daniel C, et al. Experimental study of mass transfer in a dense bubble swarm. Chem Eng Sci (2011) 66(14):3432–40. doi:10.1016/j.ces.2011.01.020

CrossRef Full Text | Google Scholar

32. Sahoo GB, Luketina D. Modeling of bubble plume design and oxygen transfer for reservoir restoration. Water Res (2003) 37(2):393–401. doi:10.1016/s0043-1354(02)00283-x

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Gong X, Takagi S, Matsumoto Y. The effect of bubble-induced liquid flow on mass transfer in bubble plumes. Int J Multiphase Flow (2009) 35(2):155–62. doi:10.1016/j.ijmultiphaseflow.2008.10.001

CrossRef Full Text | Google Scholar

34. Li G, Wang B, Wu H, DiMarco SF. Impact of bubble size on the integral characteristics of bubble plumes in quiescent and unstratified water. Int J Multiphase Flow (2020) 125:103230. doi:10.1016/j.ijmultiphaseflow.2020.103230

CrossRef Full Text | Google Scholar

35. Schaub F, Pluschkell W. Turbulent enhancement of mass transfer in bubble plumes. Chem Eng Technol Ind Chemistry-Plant Equipment-Process Engineering-Biotechnology (2006) 29(9):1073–83. doi:10.1002/ceat.200600199

CrossRef Full Text | Google Scholar

36. Gong X, Takagi S, Huang H, et al. A numerical study of mass transfer of ozone dissolution in bubble plumes with a Euler–Lagrange method. Chem Eng Sci (2007) 62(4):1081–93.

CrossRef Full Text | Google Scholar

37. Kishore N, Chhabra RP, Eswaran V. Mass transfer from a single fluid sphere to power-law liquids at moderate Reynolds numbers. Chem Eng Sci (2007) 62(21):6040–53. doi:10.1016/j.ces.2007.06.043

CrossRef Full Text | Google Scholar

38. Liu J, Zhu C, Fu T, Ma Y. Systematic study on the coalescence and breakup behaviors of multiple parallel bubbles rising in power-law fluid. Ind Eng Chem Res (2014) 53(12):4850–60. doi:10.1021/ie4037565

CrossRef Full Text | Google Scholar

39. Wang K, Luo G. Microflow extraction: a review of recent development. Chem Eng Sci (2017) 169:18–33. doi:10.1016/j.ces.2016.10.025

CrossRef Full Text | Google Scholar

40. Whitman WG The two-film theory of gas absorption. Chem Metall Eng (1923) 29:146–8.

Google Scholar

41. Higbie R. The rate of absorption of a pure gas into a still liquid during short periods of exposure. Trans Aiche (1935) 31:365–89.

Google Scholar

42. Danckwerts PV. Significance of liquid-film coefficients in gas absorption. Ind Eng Chem (1951) 43(6):1460–7. doi:10.1021/ie50498a055

CrossRef Full Text | Google Scholar

43. Ma Y, Yu G. The theoretical studies of interphase mass transfer. J Tianjin Univ (1998) 1998(04):123–7.

Google Scholar

44. Perlmutter DD. Surface-renewal models in mass transfer. Chem Eng Sci (1961) 16(3-4):287–96. doi:10.1016/0009-2509(61)80039-0

CrossRef Full Text | Google Scholar

45. Levich VG. Physicochemical hydrodynamics (1962).

Google Scholar

46. King CJ. Turbulent liquid phase mass transfer at free gas-liquid interface. Ind Eng Chem Fundamentals (1966) 5(1):1–8. doi:10.1021/i160017a001

CrossRef Full Text | Google Scholar

47. Fortescue GE, Pearson JRA. On gas absorption into a turbulent liquid. Chem Eng Sci (1967) 22(9):1163–76. doi:10.1016/0009-2509(67)80183-0

CrossRef Full Text | Google Scholar

48. Lamont JC, Scott DS. An eddy cell model of mass transfer into the surface of a turbulent liquid. AIChE J (1970) 16(4):513–9. doi:10.1002/aic.690160403

CrossRef Full Text | Google Scholar

49. Luk S, Lee YH. Mass transfer in eddies close to air-water interface. AICHE J (1986) 32(9):1546–54. doi:10.1002/aic.690320915

CrossRef Full Text | Google Scholar

50. Zedníková M, Orvalho S, Fialová M, Ruzicka M. Measurement of volumetric mass transfer coefficient in bubble columns. Chem Eng (2018) 2(2):19. doi:10.3390/chemengineering2020019

CrossRef Full Text | Google Scholar

51. Painmanakul P, Wachirasak J, Jamnongwong M, Hebrard G. Theoretical prediction of volumetric mass transfer coefficient (kLa) for designing an aeration tank. Eng J (2009) 13(3):13–28. doi:10.4186/ej.2009.13.3.13

CrossRef Full Text | Google Scholar

52. Baird MHI, Davidson JF. Gas absorption by large rising bubbles. Chem Eng Sci (1962) 17(2):87–93. doi:10.1016/0009-2509(62)80020-7

CrossRef Full Text | Google Scholar

53. Kendoush AA. Theory of convective heat and mass transfer to spherical-cap bubbles. AIChE J (1994) 40(9):1440–8. doi:10.1002/aic.690400903

CrossRef Full Text | Google Scholar

54. Takemura F, Yabe A. Gas dissolution process of spherical rising gas bubbles. Chem Eng Sci (1998) 53(15):2691–9. doi:10.1016/s0009-2509(98)00094-3

CrossRef Full Text | Google Scholar

55. Takemura F, Yabe A. Rising speed and dissolution rate of a carbon dioxide bubble in slightly contaminated water. J Fluid Mech (1999) 378:319–34. doi:10.1017/s0022112098003358

CrossRef Full Text | Google Scholar

56. Crift R, Grace JR, Weber ME. Bubbles, drops, and particles (1978).

Google Scholar

57. Nedeltchev S. Simultaneous application of penetration theory to both small and large bubbles formed in a column operated under heterogeneous regime. Chem Eng Technol Ind Chemistry-Plant Equipment-Process Engineering-Biotechnology (2008) 31(2):315–23. doi:10.1002/ceat.200700286

CrossRef Full Text | Google Scholar

58. Bao Y, Tong S, Zhang J, Cai Z, Gao Z. Reactive mass transfer of single bubbles in a turbulent flow chamber: discussion on the effects of slippage and turbulence. Chem Eng Sci (2021) 231:116253. doi:10.1016/j.ces.2020.116253

CrossRef Full Text | Google Scholar

59. Kendoush AA. Heat, mass, and momentum transfer to a rising ellipsoidal bubble. Ind Eng Chem Res (2007) 46(26):9232–7. doi:10.1021/ie070687x

CrossRef Full Text | Google Scholar

60. Alves SS, Maia CI, Vasconcelos JMT. Gas-liquid mass transfer coefficient in stirred tanks interpreted through bubble contamination kinetics. Chem Eng Process Process Intensification (2004) 43(7):823–30. doi:10.1016/s0255-2701(03)00100-4

CrossRef Full Text | Google Scholar

61. Bork O, Schlueter M, Raebiger N. The impact of local phenomena on mass transfer in gas-liquid systems. Can J Chem Eng (2005) 83(4):658–66. doi:10.1002/cjce.5450830406

CrossRef Full Text | Google Scholar

62. Kawase Y, Moo-Young M. Correlations for liquid-phase mass transfer coefficients in bubble column reactors with Newtonian and non-Newtonian fluids. Can J Chem Eng (1992) 70(1):48–54. doi:10.1002/cjce.5450700108

CrossRef Full Text | Google Scholar

63. LeClair BP, Hamielec AE. Viscous flow through particle assemblages at intermediate Reynolds numbers—a cell model for transport in bubble swarms. Can J Chem Eng (1971) 49(6):713–20. doi:10.1002/cjce.5450490601

CrossRef Full Text | Google Scholar

64. Figueroa-Espinoza B, Legendre D. Mass or heat transfer from spheroidal gas bubbles rising through a stationary liquid. Chem Eng Sci (2010) 65(23):6296–309. doi:10.1016/j.ces.2010.09.018

CrossRef Full Text | Google Scholar

65. Baird MHI, Hamielec AE. Forced convection transfer around spheres at intermediate Reynolds numbers. Can J Chem Eng (1962) 40(3):119–21. doi:10.1002/cjce.5450400307

CrossRef Full Text | Google Scholar

66. Hirose T, Moo-Young M. Bubble drag and mass transfer in non-Newtonian fluids: creeping flow with power-law fluids. Can J Chem Eng (1969) 47(3):265–7. doi:10.1002/cjce.5450470318

CrossRef Full Text | Google Scholar

67. Xu F, Cockx A, Hébrard G, Dietrich N. Mass transfer and diffusion of a single bubble rising in polymer solutions. Ind Eng Chem Res (2018) 57(44):15181–94. doi:10.1021/acs.iecr.8b03617

CrossRef Full Text | Google Scholar

68. Yin Y, Guo R, Zhu C, Fu T, Ma Y. Enhancement of gas-liquid mass transfer in microchannels by rectangular baffles. Separat Purif Technol (2020) 236:116306. doi:10.1016/j.seppur.2019.116306

CrossRef Full Text | Google Scholar

69. Gu D, Liu Y, et al. Intensification of gas-film controlled mass transfer process in a novel rotating packed bed. Chem Industry Eng Prog (2014) 33(09):2315–20.

Google Scholar

70. Budzyński P, Gwiazda A, Dziubiński M. Intensification of mass transfer in a pulsed bubble column. Chem Eng Process Process Intensification (2017) 112:18–30. doi:10.1016/j.cep.2016.12.004

CrossRef Full Text | Google Scholar

71. Zou T, Kang G, Zhou M, Li M, Cao Y. Submerged vacuum membrane distillation crystallization (S-VMDC) with turbulent intensification for the concentration of NaCl solution. Separat Purif Technol (2019) 211:151–61. doi:10.1016/j.seppur.2018.09.072

CrossRef Full Text | Google Scholar

72. Zhang W, Chen G, Li J, Liu J. Intensification of mass transfer in hollow fiber modules by adding solid particles. Ind Eng Chem Res (2009) 48(18):8655–62. doi:10.1021/ie9004964

CrossRef Full Text | Google Scholar

73. Reichert C, Hoell WH, Franzreb M. Mass transfer enhancement in stirred suspensions of magnetic particles by the use of alternating magnetic fields. Powder Technol (2004) 145(2):131–8. doi:10.1016/j.powtec.2004.06.010

CrossRef Full Text | Google Scholar

74. Jiang J, Zhao B, et al. Overview of studies on gas-liquid mass transfer enhancement in the presence of fine particles. Proc CSEE (2014) 34(05):784–92. doi:10.13334/j.0258-8013.pcsee.2014.05.011

CrossRef Full Text | Google Scholar

75. Zhang GD, Cai WF, Xu CJ, Zhou M. A general enhancement factor model of the physical absorption of gases in multiphase systems. Chem Eng Sci (2006) 61(2):558–68. doi:10.1016/j.ces.2005.07.035

CrossRef Full Text | Google Scholar

76. Ferreira A, Ferreira C, Teixeira JA, Rocha F. Temperature and solid properties effects on gas–liquid mass transfer. Chem Eng J (2010) 162(2):743–52. doi:10.1016/j.cej.2010.05.064

CrossRef Full Text | Google Scholar

77. Mena P, Ferreira A, Teixeira JA, Rocha F. Effect of some solid properties on gas–liquid mass transfer in a bubble column. Chem Eng Process Process Intensification (2011) 50(2):181–8. doi:10.1016/j.cep.2010.12.013

CrossRef Full Text | Google Scholar

78. Olle B, Bucak S, Holmes TC, Bromberg L, Hatton TA, Wang DIC. Enhancement of oxygen mass transfer using functionalized magnetic nanoparticles. Ind Eng Chem Res (2006) 45(12):4355–63. doi:10.1021/ie051348b

CrossRef Full Text | Google Scholar

79. Park SW, Choi BS, Lee JW. Effect of elasticity of aqueous colloidal silica solution on chemical absorption of carbon dioxide with 2-amino-2-methyl-1-propanol. Korea-Australia Rheology J (2006) 18(3):133–41.

Google Scholar

80. Nematbakhsh G, Rahbar-Kelishami A. The effect of size and concentration of nanoparticles on the mass transfer coefficients in irregular packed liquid–liquid extraction columns. Chem Eng Commun (2015) 202(11):1493–501. doi:10.1080/00986445.2014.947366

CrossRef Full Text | Google Scholar

81. Yin Y, Chen W, Wu C, Zhang X, Fu T, Zhu C, et al. Bubble dynamics and mass transfer enhancement in split–and–recombine (SAR) microreactor with rapid chemical reaction. Separat Purif Technol (2022) 287:120573. doi:10.1016/j.seppur.2022.120573

CrossRef Full Text | Google Scholar

82. Ganapathy H, Steinmayer S, Shooshtari A, Dessiatoun S, Ohadi MM, Alshehhi M. Process intensification characteristics of a microreactor absorber for enhanced CO2 capture. Appl Energ (2016) 162:416–27. doi:10.1016/j.apenergy.2015.10.010

CrossRef Full Text | Google Scholar

83. Zhao S, Yao C, Dong Z, Liu Y, Chen G, Yuan Q. Intensification of liquid-liquid two-phase mass transfer by oscillating bubbles in ultrasonic microreactor. Chem Eng Sci (2018) 186:122–34. doi:10.1016/j.ces.2018.04.042

CrossRef Full Text | Google Scholar

84. Liu H, Liu Y, Yu X, Huang X, Zhang J, Chen Z, et al. A novel bubble-based microreactor for enhanced mass transfer dynamics toward efficient electrocatalytic nitrogen reduction. Small (2023) 20:2309344. doi:10.1002/smll.202309344

CrossRef Full Text | Google Scholar

85. Yao X, Zhang Y, Du L, Liu J, Yao J. Review of the applications of microreactors. Renew Sustain Energ Rev (2015) 47:519–39. doi:10.1016/j.rser.2015.03.078

CrossRef Full Text | Google Scholar

86. Bojang A, Wu H. Design, fundamental principles of fabrication and applications of microreactors. Processes (2020) 8(8):891. The following symbols are used in this paper:. doi:10.3390/pr8080891

CrossRef Full Text | Google Scholar

87. Timmermann J, Hoffmann M, Schlüter M. Influence of bubble bouncing on mass transfer and chemical reaction. Chem Eng Technol (2016) 39(10):1955–62. doi:10.1002/ceat.201600299

CrossRef Full Text | Google Scholar

88. Rokoni A, Zhang L, Soori T, Hu H, Wu T, Sun Y. Learning new physical descriptors from reduced-order analysis of bubble dynamics in boiling heat transfer. Int J Heat Mass Transfer (2022) 186:122501. doi:10.1016/j.ijheatmasstransfer.2021.122501

CrossRef Full Text | Google Scholar

Glossary

www.frontiersin.org

Keywords: bubbles, gas-liquid mass transfer, mass transfer coefficient, mass transfer intensification, models

Citation: Ma Y, Guo L, Xiao Y and Ji A (2024) Bubble mass transfer in fluids under gravity: a review of theoretical models and intensification technologies in industry. Front. Phys. 12:1383537. doi: 10.3389/fphy.2024.1383537

Received: 07 February 2024; Accepted: 09 April 2024;
Published: 14 May 2024.

Edited by:

Prabhakar Sharma, Nagaland University, India

Reviewed by:

Yuyun Bao, Beijing University of Chemical Technology, China
Carlos G. Aguilar-Madera, Autonomous University of Nuevo León, Mexico
Yaran Yin, Zhejiang Sci-Tech University, China

Copyright © 2024 Ma, Guo, Xiao and Ji. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Yiyi Ma, yiyima@zju.edu.cn

Download