Fractal dimension, lacunarity, and Shannon entropy of self-assembled macroscopic copper dendrites

Macroscopic copper dendrites are self-assembled in a porous hydrogel without the application of an external potential. The copper dendrites possess fractal characteristics. The impact of the medium thickness, the initial concentration of copper (II) ions, and the solvent polarity on the evolving copper dendrites are addressed by investigating the fractal dimension, lacunarity, and Shannon entropy (SE) of the structures. The analysis gives a quantitative description of the copper dendritic morphology and its connection to the mechanism of self-assembly. The fractal dimension of the dendrites falls in the range of 1.75–1.85. High self-similar complex systems show low lacunarity and high Shannon entropy, reflecting the low density of gaps and the high level of detail.

1 Introduction

Copper dendrites synthesized over a broad range of scales have been attracting great attention due to their electrical conductivity [1], sensing [2], antibacterial [3], and catalytic [4] activity. Many methods for the preparation of copper dendrites and modification of substrates with copper dendrites have been used, including hydrothermal [5], chemical vapor [6], and electrochemical deposition [7, 8]. The methods utilized use energy and are assisted with surfactants or seed-mediated growth agents. In our study, copper dendrites are self-assembled in an agar hydrogel medium when the originally homogeneously distributed copper (II) ions in the medium are put in contact with zinc metal. The method does not require any external field, and the preparation of the copper dendrites in agar has the advantage of locking the pattern in space, thus protecting it from convectional deformation.

Dendrites are complex fractal-like spatial patterns of metals. The size and shape of dendrites have a large influence on the material’s electrical and mechanical properties [9]. Thus, a complete quantification of the branching nature of dendrites is valuable. Dendrites can be described using fractal analysis techniques. Fractals are mathematical sets that exhibit a repeating pattern displayed at every scale [10]. Fractals are characterized by a non-integer fractal dimension, which describes the complexity at the contour of a fractal. However, since the fractal dimension describes the topology in the outline, patterns with the same fractal dimension may still look different. Thus, a more complete quantification also addresses the lacunarity of the dendrite [11, 12]. Lacunarity is a term used in geometry to describe how patterns, particularly fractals, vary spatially across different scales. It is derived from the Latin word “lacuna,” which means “gap” or “lake,” and is related to the size distribution of the gaps. It allows the quantification of translational invariance with scale-dependent changes in the structure; thus, it is a measure of the texture of the fractal. There are several methods for measuring lacunarity, including box sliding algorithms, which look at a digital image from many levels of resolution to examine how certain features change with the size of the element used to inspect the image. The arrangement of pixels is measured using square elements with different sizes. For each size, a box is slid successively on the image, covering it completely, and each time it is laid down, the number of pixels that fall within the box is recorded. The local variances or changes in density are analyzed, as the observation window changes in size. Fractals with more or larger gaps generally have higher lacunarity; on the other hand, if a fractal is almost translationally invariant, it has low lacunarity. The morphological features of dendrites can also be characterized by the Shannon entropy (SE) [13], which is a fundamental concept in classical information theory. Shannon entropy quantifies the average uncertainty about a variable. In the context of spatial patterns, the Shannon entropy of a system quantifies the average amount of information needed to locate a point within the set with a certain precision. The higher the entropy of the set, the more random it is, and the more complicated are the points representing the set. The determination of Shannon information entropy in order to probe the nature of correlation effects has recently advanced and has been applied to many systems. These include the Schrödinger equation with an asymmetric rectangular multiple well [14] and squared tangent potential well [15], the two-electron ground state and lower lying excited states atomic systems [16], the eigenstates for the Pöschl–Teller-like potential [17] and a symmetrical and asymmetrical trigonometric Rosen–Morse potential [18, 19], and two hyperbolic single-well potentials in the fractional Schrödinger equation [20].

Copper dendrites under varying experimental conditions are obtained, and their fractal character is confirmed using the box-counting method for calculating the fractal dimension [21]. Fractal dimensions in the 1.75–1.85 range are obtained. Insights into the underlying processes are addressed by comparing the lacunarity of the copper dendrites at different medium thicknesses, initial Cu²⁺ concentration, and medium ionic strength. The findings are described in the context of the diffusion-limited cluster aggregation (DLCA) model for the growth mechanism [22]. The relation between the homogeneity of the fractals, characterized by their lacunarity, and the extent of self-similarity, characterized by the Shannon entropy, is investigated. The results demonstrate that highly branched homogenous fractals possess the most complex self-similar structures. Such treatments assist in the engineering and design of functional materials with the desired characteristics.

2 Materials and methods

2.1 Experimental

Agar solutions of copper (II) chloride are prepared by mixing the desired amounts of CuCl₂·2H₂O (Merck) and agar powder (Sigma-Aldrich) in distilled water. The mixtures are heated until the solutions become homogeneous. The following solutions are prepared: 1.0 M Cu²⁺ in 0.8%–1.5% with 0.1% step agar and 0.8 M, 1.2 M, 1.4 M, and 1.6 M Cu²⁺ in 1% agar. In addition, solutions with potassium chloride (Sigma-Aldrich) are prepared by adding 0.1 M, 0.2 M, 0.3 M, 0.4 M, and 0.5 M KCl to the 1.0 M Cu²⁺ and 1% agar system. A thin layer of each agar solution (13 mL) is filled in a 9-cm diameter methacrylate Petri dish. The solutions homogeneously fill the Petri dishes with no air bubbles trapped and are left to jellify overnight at room temperature. On the next day, a zinc metal (Sigma-Aldrich, purity 99.9%) formed into a 0.75 cm diameter and 1 cm height cylinder is placed at the center of each petri dish, with the one-disc face of the cylinder touching the agar solution. The systems are left to develop, and the aggregated copper dendrites at the zinc electrode are photographed 24 h after the onset of the Cu²⁺/Zn reaction. Clear images of the copper dendrites are taken from the bottom instead of the top of the Petri dish, because in few cases, morphological perturbations close to the zinc electrode occurred at the outer surface of the jellified solution. Such perturbations may be due to parameters such as dissolved and evolved gases in the solution [23]. Images are then taken for fractal analysis.

2.2 Image analysis

For fractal dimension and lacunarity analysis, the images are color-de-convoluted using Fiji: ImageJ software [24]. The color channel Giemsa vector, color 2, is selected. The selected color split gives the copper dendritic pattern standing out of the background with the most accuracy. The split is then converted to a binary black-and-white image. Figure 1 shows the original image, the split, and the binary image for the 1.0 M Cu²⁺ and 1.4% agar system as an example. Then, using FracLac [25], a plug-in for ImageJ, the fractal dimension is calculated using a box-counting algorithm, and the lacunarity is calculated using the gliding box [12] method by setting the maximum box size at 30% of the image.

Figure 1

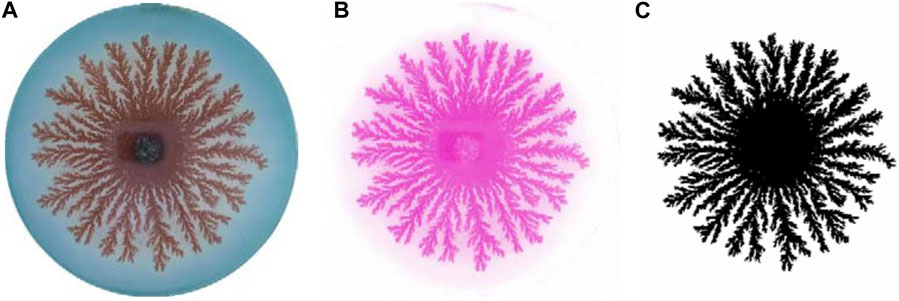
Figure 1. (A) Initial image of the copper dendrite structure for 1.0 M Cu²⁺ in the 1.4% agar system. (B) Giemsa vector color 2 channel of the system in (A). (C) Binary black-and-white contrasted image of the system in (B).

The Shannon entropy is determined by changing the dendrite image to an 8-bit grayscale format and generating the frequency distribution of the 256-pixel values using ImageJ. The region of interest (ROI) for all images is chosen as a circle with an 8.6 cm diameter. Calculations are then performed based on the relative frequency of each pixel value.

3 Results

Copper dendrites formed from 1.0 M CuCl₂·2H₂O in 0.8%, 0.9%, 1.0%, 1.1%, 1.2%, 1.3%, 1.4%, and 1.5% agar solutions are shown in Figure 2. No dendrite structures were obtained at agar percentages less than 0.8% and greater than 1.5% with 1.0 M CuCl₂·2H₂O. Copper dendrites formed from 0.8 M, 1.2 M, 1.4 M, and 1.6 M CuCl₂·2H₂O in 1% agar are shown in Figure 3. At CuCl₂·2H₂O concentrations less than 0.8 M and greater than 1.6 M in 1% agar, no dendrite structures were obtained. Dendrite structures obtained by adding 0.1 M, 0.2 M, 0.3 M, 0.4 M, and 0.5 M KCl to 1.0 M CuCl₂·2H₂O and 1% agar are shown in Figure 4. In the figures, the copper dendrites grow radially around the zinc electrode in the two-dimensional experimental setup due to the small thickness of the hydrogel medium; thus, their 2D image inspection is valid. The diameter of the ROI of the systems, as shown in Figures 1–4, is 8.6 cm.

Figure 2

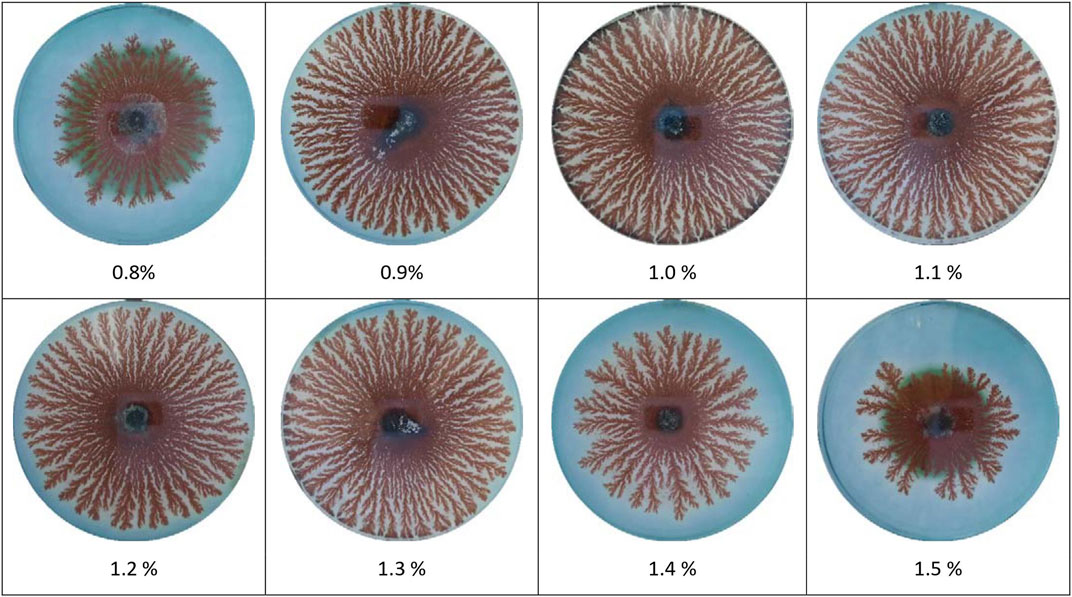
Figure 2. Copper dendrites formed from 1.0 M CuCl₂·2H₂O in agar. The corresponding agar percentage is indicated below each system.

Figure 3

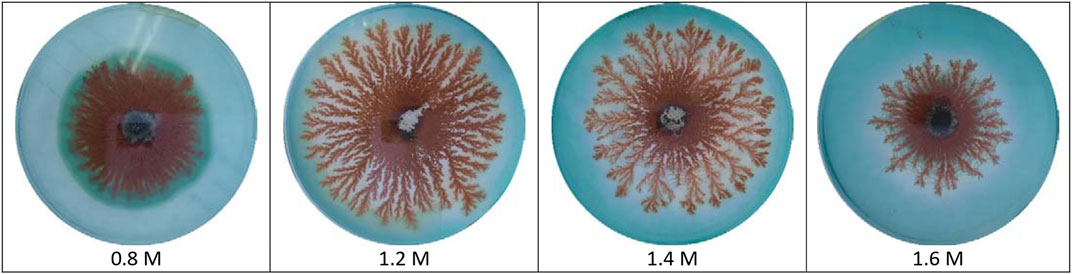
Figure 3. Copper dendrites formed from CuCl₂·2H₂O in 1% agar. The corresponding concentration of CuCl₂·2H₂O is indicated below each system.

Figure 4

Figure 4. Copper dendrites formed from 1.0 M CuCl₂·2H₂O and KCl in 1% agar. The corresponding KCl concentration is indicated below each system.

The fractal dimension is a non-integer dimension that originates from the power law relationship between the length scale and the number of objects [10]. The box-counting fractal dimension D_b is obtained from the relationship: $\ln N=D_b\mathit{ln}\left(1/r\right)+lnk$, where N is the number of boxes covering the object, r is the side of a box, and k is a constant. D_b is the slope of the linear part within the cutoff lengths in the ln N–ln (1/r) plot. The fractal dimensions for the copper dendrites shown in Figures 2–4, calculated using the box-counting method, are presented in Table 1.

Table 1

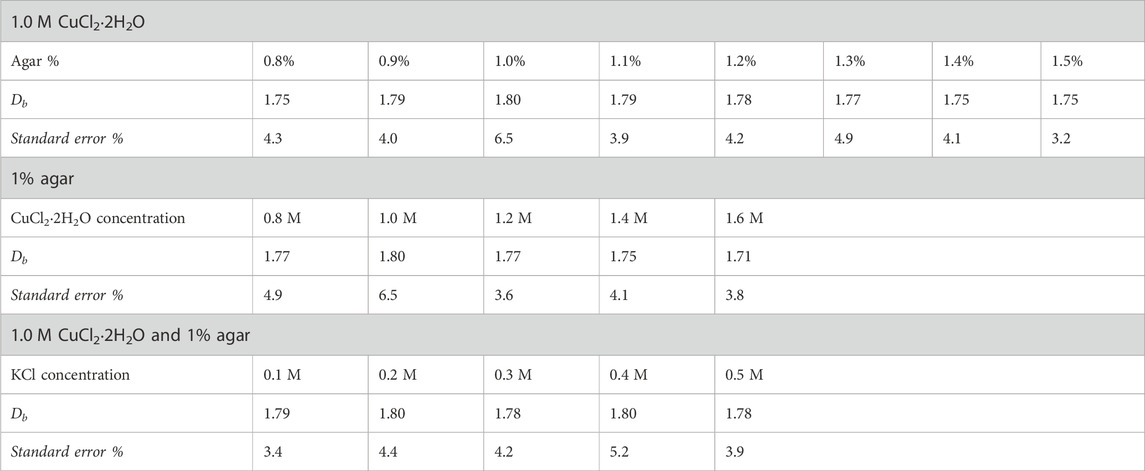
Table 1. Fractal dimension D_b calculated using the box-counting method for the dendrites in Figures 2–4.

The lacunarities of the copper dendrite fractals, shown in Figures 2–4, are determined using the gliding box method and are plotted for varying agar percentages in Figure 5A, varying Cu²⁺ concentrations in Figure 5B, and varying KCl concentrations in Figure 5C. Lacunarity analysis is a measure of the deviation of a fractal from translational invariance and thus can be considered a scale-dependent measure of the heterogeneity or texture of a fractal since translational invariance is scale-dependent [11]. Lacunarity analysis can indicate differences between structures that have the same fractal dimension. The lacunarity is calculated by adopting the gliding box method by allowing a box of size ε to move over the entire binary image with a grid orientation g, overlapping itself at each side. The basic number of lacunarity at a specific size and grid orientation is λ_ε,g, with λ_ε,g = (σ/μ)²_ε,g, where σ is the standard deviation and μ is the mean pixel per box. The mean of λ_ε,g over all box sizes E and at a grid orientation g is Λ_g with ${\mathrm{\Lambda }}_g=\left[{\displaystyle \sum _{\epsilon =1}^E}{\lambda }_{\epsilon ,g}\left(\epsilon \right)\right]/E$. Finally, the lacunarity over all grid orientations G is Λ with $\mathrm{\Lambda }=\left[{\sum }_{g=1}^G{\mathrm{\Lambda }}_g\right]/G$ [25].

Figure 5

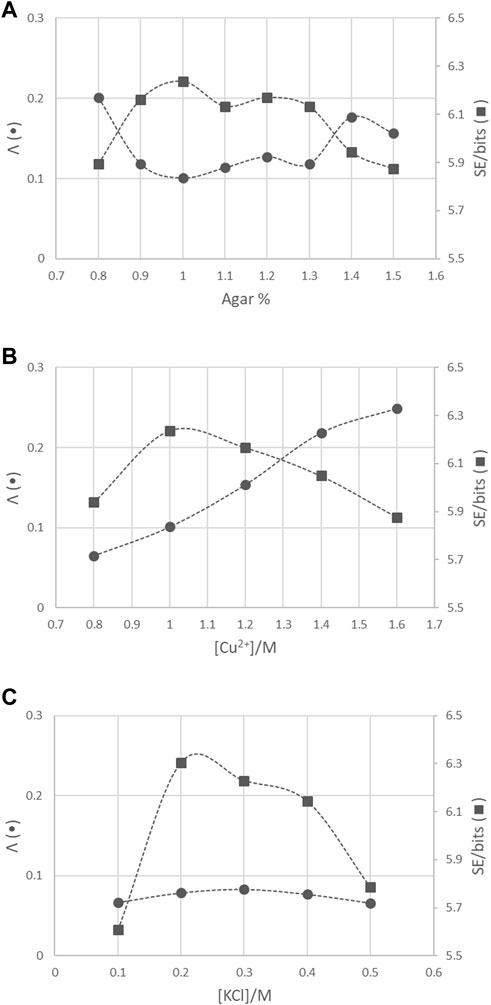
Figure 5. (A) Plots of the variations of the lacunarity (Λ) and Shannon entropy (SE) with agar percentage for 1.0 M CuCl₂·2H₂O systems. (B) Plots of the variations of the lacunarity (Λ) and Shannon entropy (SE) with the concentration of Cu²⁺ ions for the 1% agar systems. (C) Plots of the variations of the lacunarity (Λ) and Shannon entropy with the concentration of KCl for the 1.0 M CuCl₂·2H₂O in 1% agar systems. The lines connecting the points are only an aid for the eye.

The Shannon entropy of the copper dendrite fractals shown in Figures 2–4 is plotted for varying agar percentages in Figure 5A, varying Cu²⁺ concentrations in Figure 5B, and varying KCl concentrations in Figure 5C. The Shannon entropy captures the complexity and degree of detail in the fractal structure. The Shannon entropy is computed based on the relative frequency/probability p_i of the 256-pixel values in the grayscale format of each fractal structure; $SE={\sum }_{i=0}^{255}{p}_i{\mathit{log}}_2\left({1/p}_i\right)$ [26]. Finally, Figure 6 shows a plot of the Shannon entropy as a function of fractal dimension D_b for different agar percentages and 1.0 M CuCl₂·2H₂O concentration.

Figure 6

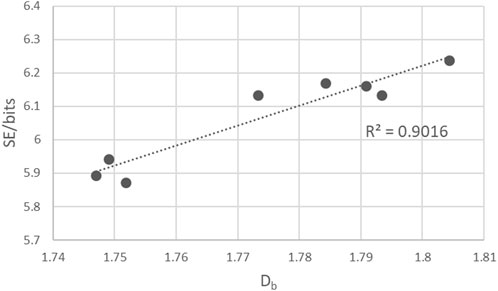
Figure 6. A plot of the variation of the fractal dimension (D_b) with Shannon entropy (SE) for copper dendrites obtained with 1.0 M CuCl₂·2H₂O at different agar percentages. The dotted line is the best fit of the experimental points.

4 Discussion

The diffusion-limited cluster aggregation is a widely used model that describes the generation of clusters from colloidal aggregation driven by Brownian motion [27, 28]. The growth process can be used to describe the formation of fractal-like electrodeposits and metal dendrites. In DLCA, randomly moving colloids, upon entering the interaction region of a growing cluster, will irreversibly combine with it. Compared to diffusion-limited aggregation (DLA) [29, 30], which involves individual particles performing random walks and aggregating on the growing structure, DLCA involves the aggregation of colloids, thus leading to more complex structures. In the Cu²⁺/Zn system, the copper (II) ions are originally homogeneously distributed in the agar medium. When zinc metal is set in contact with the agar solution, the fast thermodynamically favorable oxidation–reduction reaction, Zn (s) + Cu²⁺ (aq) → Zn²⁺ (aq) + Cu (s), takes place at the zinc metal, and the reduction of copper (II) ions to copper metal starts. Based on the values of the fractal dimension obtained for our systems shown in Table 1, which are almost the same and fall in the 1.75–1.85 range characteristic of DLCA, the mechanism involves the formation of colloids before clustering on the growing dendrite. This deposition of copper will deplete the electrode region from copper (II) ions and thus lead to the migration of peripheral Cu²⁺ ions toward the growing electrode due to the concentration gradient. The arriving copper (II) ions will undergo reduction, followed by colloid formation, and then clustering. The smallest value of the fractal dimension 1.71, which is also below the DLCA range, is obtained only for the 1.6 M CuCl₂·2H₂O in 1% agar. This value is close to the 1.7 limit value for DLA and suggests the shift of the mechanism to solely diffusion-limited, or alternately, it confirms the decrease in fractal dimension as the primary particle radius increases in DLCA [31] at the highest Cu²⁺ concentration. In all instances, the copper fractals arise as a joint consequence of randomness and optimality [32]. Randomness is due to the Brownian motion of the ions or clusters, and optimality is the optimal energy expenditure along energetically favorable crystallographic directions on the growing dendrite. Furthermore, the fact that fractal formation is restricted to the experimental ranges, as shown in Table 1, confirms that the aggregation of copper dendrites in porous media is a complex multi-parametric phenomenon.

Distinctions between the textures of the copper dendrites with varying agar percentages, Cu²⁺ initial concentration, and the presence of an inert salt are elucidated by addressing the lacunarity of the systems. The lacunarity in Figure 5A for systems with 1 M CuCl₂·2H₂O is almost the same and the lowest at the intermediate agar percentages. The low values of lacunarity for 0.9%, 1%, 1.1%, 1.2%, and 1.3% agar reflect less density of gaps and more uniformity in the structures than in the less developed structures at the lowest and highest agar percentages, as shown in Figure 2. Although the migration of Cu²⁺ ions toward the growing electrode becomes slower as the porosity of the medium decreases with increasing agar percentage, branching depends more on the extent of aggregation than on the rate of diffusion of ions. On the other hand, an increase in lacunarity and thus an increase in the density of gaps and inhomogeneity of the systems are obtained by increasing the initial concentration of copper (II) ions at 1% agar, as shown in Figure 3 and Figure 5B. With increasing copper ion concentrations, the primary particle radius increases [31]. This dominance of the growth of the colloids over clustering leads to less branching and results in less dense dendrites. Finally, the most homogeneous and branched structures with the lowest lacunarity are obtained after the addition of the inert salt KCl to the 1.0 M CuCl₂·2H₂O and 1% agar systems, as shown in Figure 4 and Figure 5C, respectively. Due to the presence of K⁺ and Cl⁻ charge carriers that increase the ionic strength of the medium, metallic copper nuclei formation, on which colloids grow via diffusion, is enhanced, thus forming islands that, upon connection, form fractals with high branching and low lacunarity.

The degree of uncertainty and randomness in the copper dendrite structures is also addressed by calculating the Shannon entropy using the frequencies of the different intensity levels in the grayscale images [33, 34]. Shannon entropy has been effective in describing the degree of disorder in a diversity of disciplines [35–37]. The Shannon entropy obtained for the copper dendrite fractals falls between 5.6 bits and 6.3 bits, as shown in Figure 5. The values are within the 0 bits and 8.1 bits range for a pool of 256-pixel variables. High entropy values indicate that the pixel intensities are diverse and less predictable, representing a self-similar pattern. Conversely, low entropy values indicate that the pixel intensities are uniform and predictable, representing a less detailed pattern. The variations in lacunarity and Shannon entropy for the copper dendrites are consistent, as shown in Figure 5. For systems with high lacunarity values reflecting the high density of voids, the Shannon entropy and, thus, the level of detail are low and vice versa, as shown in Table 2. The most detailed and complex structure with the highest Shannon entropy and a low lacunarity is 1.0 M CuCl₂·2H₂O and 0.2 M KCl in 1% agar.

Table 2

Table 2. Characteristics of systems with low lacunarity and high Shannon entropy.

Although the fractal dimension and Shannon entropy are two measures that capture different aspects of the pattern, where the fractal dimension focuses on the complexity and self-similarity at the contour of the fractal, while the Shannon entropy concentrates on the overall complexity of the pattern, a linear positive correlation between the two is obtained for systems with varied agar percentages, as shown in Figure 6. This result confirms the relationship between the Renyi entropy S_q [34, 38], which is a generalization of the Shannon entropy, and the fractal dimension, given by the equation S_q(ε) = -D_b log_b(ε). Here, q is the order of Renyi entropy, and ε refers to the sides of boxes for measurements expressed at base b logarithm. The Renyi entropy converges to the Shannon entropy as q → 1. This behavior indicates that the information content at different scales is consistently changing in a linear manner.

5 Conclusion

Spatial copper dendrite patterns with fractal characteristics are self-assembled without the intervention of an external field. The morphologies of the patterns are described by determining the lacunarity and Shannon entropy of the systems. The physical characteristics are explained on the basis of ion dynamics and colloid clustering in different agar porosities and solutions with different ionic strengths. The variations in lacunarity and Shannon entropy obtained are consistent in the sense that systems with high lacunarity values, reflecting the high density of gaps, possess low Shannon entropy, reflecting a low level of detail and hence self-similarity. In addition, a linear relationship is obtained between the fractal dimension and Shannon entropy, reflecting the self-similar nature of the copper dendrite systems.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

LB: conceptualization, formal analysis, methodology, writing–original draft, and writing–review and editing. JS: investigation, validation, and writing–original draft.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors thank the Department of Sciences at Notre Dame University–Louaize for acquiring the chemicals and materials.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Toigoa C, Frankenberger M, Billot N, Pscherer C, Stumper B, Distelrath F, et al. Improved Li₄Ti₅O₁₂ electrodes by modified current collector surface. Electrochimica Acta (2021) 392:138978. doi:10.1016/j.electacta.2021.138978

CrossRef Full Text | Google Scholar

2. Zhang X, Wang G, Liu X, Wu H, Fang B. Copper dendrites: synthesis, mechanism discussion, and application in determination of L-tyrosine. Cryst Growth Des (2008) 8(4):1430–4. doi:10.1021/cg7011028

CrossRef Full Text | Google Scholar

3. Zhou E, Qiao D, Yang Y, Xu D, Lu Y, Wang J, et al. A novel Cu-bearing high-entropy alloy with significant antibacterial behavior against corrosive marine biofilms. J Mater Sci Technology (2020) 46:201–10. doi:10.1016/j.jmst.2020.01.039

CrossRef Full Text | Google Scholar

4. Zhao L, Yuan Z, Ma B, Ding X, Tian Y, Yang X. Regulation of three-dimensional hydrophobic state of copper dendrite adjusts the distribution of liquid products from electrochemical reduction of CO₂. Appl Surf Sci (2023) 628:157369. doi:10.1016/j.apsusc.2023.157369

CrossRef Full Text | Google Scholar

5. Truong QD, Kakihana M. Hydrothermal growth of cross-linked hyperbranched copper dendrites using copper oxalate complex. J Cryst Growth (2012) 348(1):65–70. doi:10.1016/j.jcrysgro.2012.03.052

CrossRef Full Text | Google Scholar

6. Abuhimd H. Low-pressure chemical vapor deposition copper nanodendrites growth design. Arabian J Sci Eng (2017) 42:1371–9. doi:10.1007/s13369-016-2246-8

CrossRef Full Text | Google Scholar

7. Nikolić ND, Popov KI, Pavlović LJ, Pavlović MG. Morphologies of copper deposits obtained by the electrodeposition at high overpotentials. Surf Coat Technology (2006) 201(3-4):560–6. doi:10.1016/j.surfcoat.2005.12.004

CrossRef Full Text | Google Scholar

8. Gupta R, Ghosh S, Choudhury S, Ghosh S. Pattern transition from dense branching morphology to fractal for copper and β′ brass electrodeposition in thin gap geometry. AIP ADVANCES (2018) 8:015219. doi:10.1063/1.5007110

CrossRef Full Text | Google Scholar

9. Zasadzinska M, Knych T, Smyrak B, Strzepek P. Investigation of the dendritic structure influence on the electrical and mechanical properties diversification of the continuously casted copper strand. Materials (2020) 13:5513. doi:10.3390/ma13235513

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Mandelbrot BB. Fractal geometry of nature. New York: W. H. Freeman and Company (1982).

Google Scholar

11. Gefen Y, Meir Y, Mandelbrot BB, Aharony A. Geometric implementation of hypercubic lattices with noninteger dimensionality by use of low lacunarity fractal lattices. Phys Rev Lett (1983) 50:145–8. doi:10.1103/physrevlett.50.145

CrossRef Full Text | Google Scholar

12. Allain C, Cloitre M. Characterizing the lacunarity of random and deterministic fractal sets. Phys Rev A (1991) 44(6):3552–8. doi:10.1103/physreva.44.3552

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Shannon CE. A mathematical theory of communication. Bell Syst Tech (1948) J(3):379–423. doi:10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

14. Santana CR, Dong Q, Sun G-H, Silva-Ortigoza R, Dong S-H. Shannon entropy of asymmetric rectangular multiple well with unequal width barrier. Results Phys (2022) 33:105109. doi:10.1016/j.rinp.2021.105109

CrossRef Full Text | Google Scholar

15. Dong S, Sun G-H, Dong S-H, Draayer JP. Quantum information entropies for a squared tangent potential well. Phys Lett A (2014) 378:124–30. doi:10.1016/j.physleta.2013.11.020

CrossRef Full Text | Google Scholar

16. Lin C-H, Ho Y-K. Shannon information entropy in position space for two-electron atomic systems. Chem Phys Lett (2015) 633:261–4. doi:10.1016/j.cplett.2015.05.029

CrossRef Full Text | Google Scholar

17. Sun G-H, Aoki MA, Dong S-H. Quantum information entropies of the eigenstates for the Pöschl-Teller-like potential. Chin Phys. B (2013) 22(5):050302. doi:10.1088/1674-1056/22/5/050302

CrossRef Full Text | Google Scholar

18. Sun G-H, Dong S-H. Quantum information entropies of the eigenstates for a symmetrically trigonometric Rosen–Morse potential. Phys Scr (2013) 87(4):045003. doi:10.1088/0031-8949/87/04/045003

CrossRef Full Text | Google Scholar

19. Sun G-H, Dong S-H, Saad N. Quantum information entropies for an asymmetric trigonometric Rosen-Morse potential. Ann Phys (Berlin) (2013) 525(12):934–43. doi:10.1002/andp.201300089

CrossRef Full Text | Google Scholar

20. Santana-Carrillo R, González-Flores JS, Magana-Espinal E, Quezada LF, Sun G-H, Dong S-H. Quantum information entropy of hyperbolic potentials in fractional schrödinger equation. Entropy (2022) 24:1516. doi:10.3390/e24111516

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Bouda M, Caplan JS, Saiers JE. Box-counting dimension revisited: presenting an efficient method of minimizing quantization error and an assessment of the self-similarity of structural root systems. Front Plant Sci (2016) 7:149. doi:10.3389/fpls.2016.00149

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lin MY, Lindsay HM, Weitz DA, Ball RC, Klein R, Meakin P. Universality in colloid aggregation. Nature (1989) 339:360–2. doi:10.1038/339360a0

CrossRef Full Text | Google Scholar

23. Nie Z, Peng K, Lin L, Yang J, Cheng Z, Gan Q, et al. A conductive hydrogel based on nature polymer agar with self-healing ability and stretchability for flexible sensors. J Chem Eng (2023) 454(1):139843. doi:10.1016/j.cej.2022.139843

CrossRef Full Text | Google Scholar

24. Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, et al. Fiji: an open-source platform for biological-image analysis. Nat Methods (2012) 9(7):676–82. doi:10.1038/nmeth.2019

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Karperien A. FracLac for ImageJ (2024). Available at: http://rsb.info.nih.gov/ij/plugins/fraclac/FLHelp/Introduction.htm1999-2013 (Accessed date: 24 July 2023).

Google Scholar

26. Aczél J. Entropies, characterizations, applications and some history. Mod Inf Process (2006) 3–10. doi:10.1016/b978-044452075-3/50001-7

CrossRef Full Text | Google Scholar

27. Meakin P. Fractal aggregates. Adv Colloid Interf Sci. (1987) 28:249–331. doi:10.1016/0001-8686(87)80016-7

CrossRef Full Text | Google Scholar

28. Moncho-Jordá A, Martınez-López F, Hidalgo-Álvarez R. Simulations of aggregation in 2D. A study of kinetics, structure and topological properties. Phys A: Stat Mech Appl (2000) 282(1-2):50–64. doi:10.1016/s0378-4371(00)00069-8

CrossRef Full Text | Google Scholar

29. Witten TA, Sander LM. Diffusion-limited aggregation. Phys Rev B (1983) 27:5686–97. doi:10.1103/physrevb.27.5686

CrossRef Full Text | Google Scholar

30. Kan X, Chen K, Yin C, Yang Y, Shan M, Wang H, et al. Self-Organized fractal structures on plasma-exposed silver surface. Front Chem (2021) 9:816811. doi:10.3389/fchem.2021.816811

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wu H, Lattuada M, Morbidelli M. Dependence of fractal dimension of DLCA clusters on size of primary particles. Adv Colloid Interf Sci. (2013) 195-196:41–9. doi:10.1016/j.cis.2013.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Bak P, Tang C, Wiesenfeld K. Self-organized criticality. Phys Rev A (1988) 38:364–74. doi:10.1103/physreva.38.364

CrossRef Full Text | Google Scholar

33. Wachinger C, Navab N. Entropy and Laplacian images: structural representations for multi-modal registration. Med Image Anal (2012) 16(1):1–17. doi:10.1016/j.media.2011.03.001

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Zmeskal O, Dzik P, Vesely M. Entropy of fractal systems. Comput Math Appl (2013) 66:135–46. doi:10.1016/j.camwa.2013.01.017

CrossRef Full Text | Google Scholar

35. Conforte AJ, Tuszynski JA, Silva FAB, Carels N. Signaling complexity measured by Shannon entropy and its application in personalized medicine. Front Genet (2019) 10:930. doi:10.3389/fgene.2019.00930

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Cincotta PM, Giordano CM, Silva RA, Beaugé C. The Shannon entropy: an efficient indicator of dynamical stability. Physica D (2021) 417:132816. doi:10.1016/j.physd.2020.132816

CrossRef Full Text | Google Scholar

37. Ma CW, Ma YG. Shannon information entropy in heavy-ion collisions. Prog Part Nucl Phys (2018) 99:120–58. doi:10.1016/j.ppnp.2018.01.002

CrossRef Full Text | Google Scholar

38. Chen Y. Equivalent relation between normalized spatial entropy and fractal dimension. Physica A (2020) 553:124627. doi:10.1016/j.physa.2020.124627

CrossRef Full Text | Google Scholar