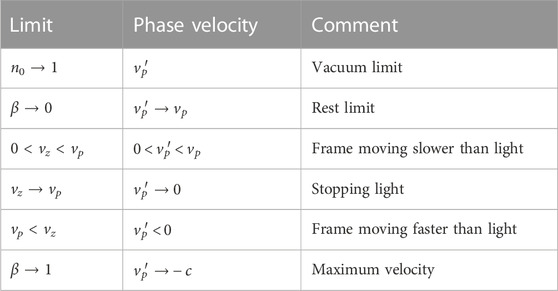
Special theory of relativity for a graded index fibre

1 Introduction

Einstein created a legacy with the establishment of the theory of relativity [1, 2], which continues to attract a wide range of researchers and engineers more than a century later. The story goes that Einstein considered how light would be seen by an observer travelling as fast as the speed of the light [3], leading to the discovery of the law that the speed of light (c) and the propagation of light in a vacuum is independent of the frame of reference of any observer, as inferred by Maxwell equations [4, 5]. The universal relationship of space and time through the Lorentz transformation led to various non-trivial results, such as Doppler effects of light, time dilation, length contraction, and the energy-momentum relationship of $E^2={(cp)}^2+{(m_0{c}^2)}^2$, where E is energy, p is momentum, m₀ is the rest mass of an object [1, 2, 4, 6–9]. In order to satisfy causality, it is strictly forbidden to allow motion faster than c [1, 2, 4].

Nevertheless, inside a material, a speed of a moving frame can exceed the speed of light due to a larger refractive index (n) than one of a vacuum, as experimentally proved by Cherenkov radiation [10–12]. A charged particle with a speed exceeding the phase velocity of light in a material produces a coherent shock wave, similar to the sonic waves made by a supersonic aircraft. Cherenkov radiation is usually observed in water as a bluish conical ray, emitted from a charged elementary particle, which enabled physicists to observe neutrino oscillations [13]. Here, we would like to revisit the original proposition of Einstein: how light is seen in a material by an observer, when travelling at a speed exceeding the phase velocity of light?

Our motivation is to understand the internal quantum structure of a photon, particularly to gain insights to clarify the correlation between spin and polarisation [14–17]. One might think that it is firmly well-established that the spin of photons describes the polarisation of light [4, 5, 18–23], such that the correlation is obvious. However, this is highly non-trivial, as implied by Einstein, confessing that he could not understand what light quanta are at all after 50 years of continuous consideration [3], regardless of the fact that he established a theory for a photoelectric effect as evidence of the particle nature of the photon.

We have a hypothesis that the polarisation of light is a macroscopic manifestation of the spin of a photon as a quantum-mechanical feature. We have shown that a wavefunction of a photon is described by a Helmholtz equation [4, 5, 14], which does not necessarily give a plane-wave form and the solution depends on a profile of the refractive index and a symmetry of system. A ray of photons, emitted from a laser source, is described by a many-body coherent state [14–17, 24–29] with fixed phases, which describe an SU(2) state for the spin state of macroscopically condensed photons. By calculating the quantum-mechanical average of spin operators, we have shown that the expectation values of spin of photons are actually Stokes parameters in Poincaré sphere [14, 30, 31]. The magnitude of spin becomes $S_0=\hslash \mathcal{N}$, where S₀ is the Stokes parameter for the magnitude of polarisation, ℏ is the Dirac constant, and $\mathcal{N}$ is the number of photons in a system, for a coherent ray of photons, which implies that the effective Planck constant becomes a macroscopic value, leading to a macroscopic realisation of a quantum state as polarisation [14]. The photonic orbital angular momentum is also a well-defined quantum-mechanical observable [15, 16, 32], and we have shown that we can split spin and orbital angular momentum from the total optical angular momentum [4, 5, 16, 24, 32, 33, 33, 34, 34, 34, 35, 35–40] in a GRaded-INdex (GRIN) fibre [41], where the exact solution is available based on a Laguerre-Gauss mode [16]. The spin of a photon is derived by a two-dimensional (2D) space-time Dirac equation from the principle of rotational symmetry for the quantum-mechanical state of a photon [17]. Based on these considerations [14–17], we believe that the coherent spin state of photons from a laser source is characterised by a broken symmetry state due to the Bose-Einstein condensation of photons, enabled by pumping above the lasing threshold [17]. Consequently, the macroscopically coherent ray of photons from a laser source is described by a single SU(2) wavefunction such as a Jones vector [5], a chiral Bloch state [18, 19], and a diagonal state [14]. Thus, a simple quantum-mechanical calculation of a spin state is applicable to a coherent photonic ray using a single particle wave function, and its manipulation is also straightforward by employing a phase-shifter and a rotator to change the phases of the wave function [14].

The aim of this paper is to understand the photonic state in a material seen by an observer travelling at a speed comparable to or even greater than the speed of light. In a photonic crystal [42] or an optical fibre [5], the dispersion relationship of a photon is precisely engineered to adjust the speed of light and other photonic properties. We consider a uniform material and a GRIN fibre as examples because we can treat the dispersion exactly, in an analytic way.

2 Principle

2.1 Lorentz transformation

We are not challenging the established Lorentz transformation at all [1, 2, 4, 43–47]. The energy scale we are considering is of the order of 1 eV such as for fibre optics, such that the space-time relationship of the vacuum must be robust in the presence of a material. We assume the rest frame of (t, x, y, z), where fibre optic materials are located, and consider how the light will be observed by the moving from of (t′, x′, y′, z′) at the speed of v_z along the positive +z direction. The Lorentz transformation, L, whose determinant is unity, det(L) = 1, is defined by.

where a² − b² = 1, and parameters a and b are determined by the principle of relativity, guaranteeing that the speed of light in a vacuum is independent of the measurement frame. In order to impose the principle, we start from the Helmholtz equations in a vacuum.

where Ψ(t, x, y, z) and Ψ′(t′, x′, y′, z′) are wavefunctions of a photon for the frames (t, x, y, z) and (t′, x′, y′, z′), respectively. The wave equations can be obtained from the Maxwell equation [4, 5]. We define the 2D d’Alembertian operators as

such that the wave equations are simply shown as.

Einstein’s postulate of the universal speed of light in a vacuum corresponds to impose [4, 5]

By inserting the identity

into d’Alembertian, we obtain

where dz′/dt′ = −v_z at dz/dt = 0. Then, we obtain a and b, and L becomes a standard form [1, 2, 4, 43] of

where $\gamma =1/\sqrt{1-{\beta }^2}$ and the normalised velocity of the moving frame is given by β = v_z/c. By using the Lorentz transformation, the d’Alembertian is always invariant in a vacuum, such that the velocity of light is constant and independent of the choice of the frame. We can also consider the inverse Lorentz transformation as.

which is equivalent to exchange.

in the original Lorentz transformation, reflecting the principle of relativity. The Lorentz transformation is valid in our argument.

2.2 Schödinger equation for a photon

In a material, the dispersion relationship for a photon is highly non-trivial. In order to provide a specific example, we chose a GRIN fibre, where the exact solution is available [5, 14–17, 41]. The refractive index of a GRIN fibre (n_ind) is given by $n_{\text{ind}}^2=n_0^2\left(1-{(gr)}^2\right)$, where n₀ is the refractive index of the core, g is the graded index parameter, and r is the radius in a cylindrical coordinate of (r, ϕ, z). Then, the Helmholtz equation for a GRIN fibre in the rest frame becomes

A solution in the cylindrical coordinate is given by Ψ(t, x, y, z) = ψ(r, ϕ)ψ_z, where the radial and angular dependences of the wavefunction, ψ(r, ϕ), for a photon in a GRIN fibre can be decoupled by using the Laguerre-Gauss mode [5, 14–17, 32] as

, which is equivalent to integrating these degrees of freedom in a Feynman path integral formalism [14–17, 27–29]. After eliminating (r, ϕ), we confirm the dispersion relationship with the opening up of the energy gap

where the overall shift of the energy is ℏδw₀ = v₀g, n is the radial quantum number, m is the magnetic orbital angular momentum along the principal axis of z, and m* is the effective mass of the photon in a GRIN fibre [14–17, 27–29]. Please note the similarity of the original Einstein theory of relativity to assign the rest mas of m to its energy as E = mc² [1, 2]. The emergence of the effective mass is attributed to the broken SU(2) symmetry of photons due to lasing [17]. It is interesting to note that the obtained dispersion relationship is quite similar to the Bardeen-Cooper-Schrieffer (BCS) theory of superconductivity [48–54]. The remaining degree of freedom is the propagation of light along z in a GRIN fibre, which is described by the Schrödinger-like equation

where ψ_z is the wavefunction of a photon, ℏ = h/(2π) is the Dirac constant, and we have re-defined the d’Alembertian.

to account for the reduced speed of light in a material. The wavefunction along z becomes a simple plane wave,

while the dispersion for the guided mode [17] becomes

In deriving this energy-momentum dispersion relationship, we assumed de-Broglie relationship.

where ω is the angular frequency and k = 2π/λ is the wavenumber for the photon with the wavelength of λ.

2.3 Lorentz transformation in a uniform material

First, we examine the weak coupling limit of g → 0. In this case, the energy gap vanishes, Δ → 0, and the wave equation becomes

Thus, a photon is massless with the reduced velocity of v₀ in a uniform material of the refractive index of n₀. The dispersion relationship is linear,

and the phase velocity v_p is given by v_p = v₀ = c/n₀.

By applying the Lorentz transformation to the wave equation, we obtain the corresponding wave equation in the moving frame as

Inserting the trial function of the form,

we obtain the dispersion relationship in the moving frame,

The phase velocity in the frame is given by

We can obtain the same dispersion relationship, by simply inserting the Lorentz transformation into the original wavefunction as

which leads

2.3.1 Vacuum limit

We check the obtained dispersion in the known limit of the vacuum, such that we take the limit of n₀ → 1. In this case, we reproduce a standard theory of relativity [1, 2, 4]. We obtain.

from which we obtain the Doppler effect for the light by setting k′ = 2π/λ′, we obtain

We expect red-shift for v_z > 0, since the light source is relatively moving away, such that the wavelength is elongated for the observer moving away from the light source. On the other, the blue-shift is expected for v_z < 0, since the light source is approaching the observer. We can also confirm the principle of relativity by exchanging λ ↔ λ′ and β ↔ − β at the same time, the relationship between λ and λ′ are not altered.

2.3.2 Uniform material

We assumed the material is at rest in the frame of (t, x, y, z) and the moving frame of (t′, x′, y′, z′) is not equivalent to the original frame anymore. In this case, the wavenumber of k′ is always positive, while the angular frequency of ω′ can change its sign upon increasing the frame velocity of β. Consequently, the phase velocity of $v_p^{\prime }$ can also change sign, such that the light is seen to be propagating the backward if the frame is moving faster than the speed of light in a material, which is indeed possible as is known for the case of the Cherenkov radiation [10–12]. We can see the consequence of the Lorentz transformation by examining several typical limits of the obtained phase velocity of $v_p^{\prime }$ (Table 1). The details of the calculated parameters are discussed in the next section (Figure 1).

TABLE 1. The phase velocity of light observed from a moving frame in a uniform material.

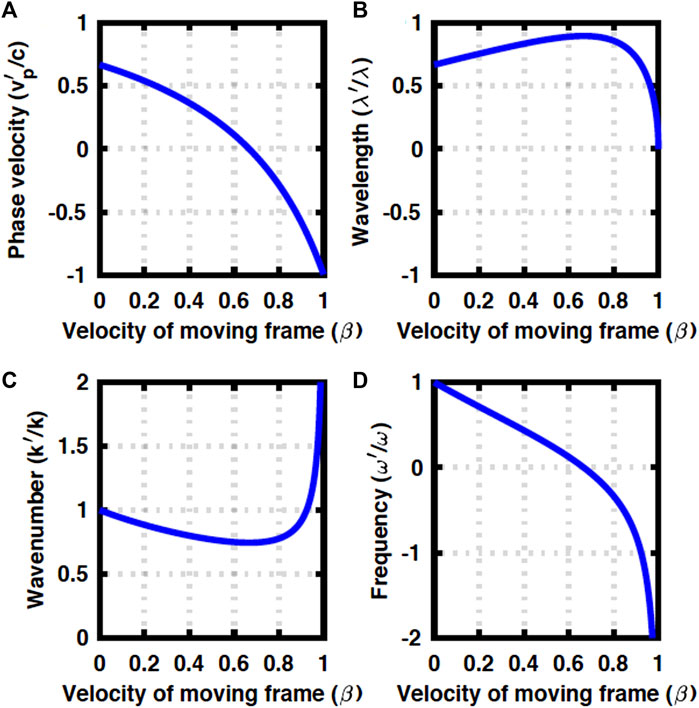
FIGURE 1. Doppler effects in a uniform material are observed from a moving frame. (A) Phase velocity changes sign at v_z = v_p. (B) Wavelength is red-shifted for v_z < v_p, while it starts to exhibit blue-shift for v_p < v_z. (C) Wavenumber is always positive, while (D) frequency changes sign.

2.4 Lorentz transformation in a GRIN fibre

In a GRIN fibre, the dispersion relationship is different from a uniform material, due to the band-gap opening, as we have outlined above [5, 14–17, 32]. We can obtain the corresponding dispersion relationship observed in a moving frame. The main assumption is the plane waveform of the solution along z and t and the validity of the space-time relationship by the Lorentz transformation. Consequently, we obtain

which gives

The relationship is simply summarised as the Lorentz transformation of

This is equivalent to imposing the de-Bloglie relationship in the moving frame as

which gives the Lorentz transformation of the energy-momentum relationship as

which must be valid for an arbitrary dispersion E = E(p) beyond the dispersion for a GRIN fibre. The relative symmetry against a frame exchange does not exist anymore with a material, because the rest frame with a material is different from the moving frame. Consequently, we obtain non-trivial Doppler effects, as shown in the next section.

3 Results

3.1 Doppler effects in a uniform material

First, we show numerical results in a uniform material (Figure 1). We assumed n₀ = 1.5 and Δ = 0, and the wavelength of λ = 1.5 μm, considering typical parameters of a glass fibre [5]. Upon increasing the frame velocity of β, the phase velocity of $v_p^{\prime }$ decreases and changes sign at v_z = v_p and $v_p^{\prime }$ approaches −c in the maximum limit of β → 1 (Figure 1A).

We expect a red-shift for v_z < v_p, since the observer in the moving frame is going away from the light source in the rest frame, such that the wavelength is elongated, while blue-shift is expected for v_p < v_z (Figure 1B). By assuming k′ = 2π/λ′, we obtain the wavelength in the moving frame

We confirm the appropriate limit of λ′ → λ for β → 0, while the limit of λ′ → 0 for β → 1 might be non-trivial. We expect the peak of the wavelength at

which indeed gives v_z = v_p. We are considering the continuous wave, emitted from the light source in the rest frame, rather than a pulsed operation. If the frame is moving above the speed of light in the rest frame, the frame is approaching the light, which was emitted earlier, such that the wavelength of the light is observed shorter than that in the rest frame. The wavenumber is always positive (Figure 1C), since the refractive index of a material is always larger than unity (n₀ > 1) and the frame cannot move larger than c (β < 1).

On the other hand, the angular frequency of ω′ changes signs at v_z = v_p, such that the polarisation state starts to rotate in the opposite way as if the time is going backward (Figure 1D). This could be considered by defining a chiral operator defined by

In the moving frame, we consider

which changes sign at v_z = v_p. Therefore, the helicity is reversed upon increasing β.

In this work, we have a priori assumed that the clocks in the rest frame and the moving frame are completely synchronised, which is far from trivial [45–47, 55, 56]. In fact, the one-way speed of light cannot be measured without properly defining how to synchronize the clocks among frames [45–47, 55–57]. Therefore, it is better to measure the speed of light in round-trip (two-way) measurements. Theoretical challenges to go beyond the Lorentz invariance were also reported [46, 58]. It is beyond the scope of this work to invent the actual measurement set-up to observe the Doppler effects found in Figure 1. We have naively applied the standard special theory of relativity for the lights propagating in a material, but, the results could be interpreted in conjunction with the definition of clocks and the measurement set-up [45–47, 55–58].

3.2 Doppler effects in a GRIN fibre

Next, we consider the Doppler effects in a GRIN fibre. We assume the same core of n₀ for the wavelength of λ = 1.5 μm, while the energy gap of Δ is chosen as a parameter.

The numerical results at Δ = 0.2ℏω are shown in Figure 2. The qualitative features are not changed in the case of a uniform material (Figure 1). The critical frame velocity, required to change the sign of the phase velocity, is increased due to the opening of the band gap (Figure 2A). We expect more significant red- and blue-shifts upon increasing β (Figure 2B), but k′ is always positive and ω′ changes sign, as before.

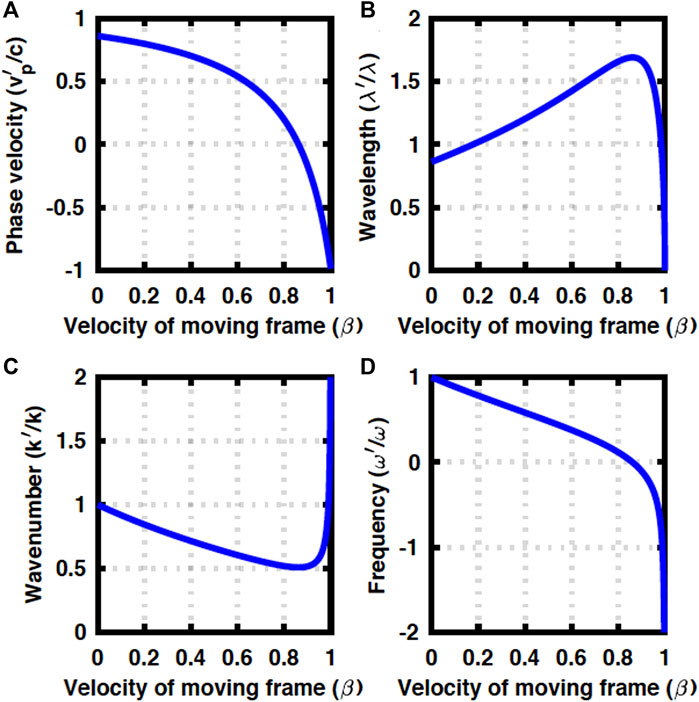
FIGURE 2. Doppler effects in a GRIN fibre at Δ = 0.2ℏω. (A) Phase velocity, (B) wavelength, (C), wavenumber, and (D) frequency.

On the other hand, for the larger Δ at 0.4ℏω, Doppler effects are even more anomalous. In this case, k′ changes sign, while ω′ is always positive. This is attributed to the larger contributions to the total energy of ℏω from orbital degrees of freedoms through the radial oscillations and/or photonic orbital angular momentum, characterised by n and m [5, 14–17, 32]. As a result, the contribution of the kinetic energy for the propagation along z is limited, such that the frame is easier to go beyond the speed of the light, which allows k′ to change the sign (Figure 3A). For k′ < 0, we have assumed k′ = −2π/λ′ to extract the wavelength of λ′ in the moving frame (Figures 3B–D).

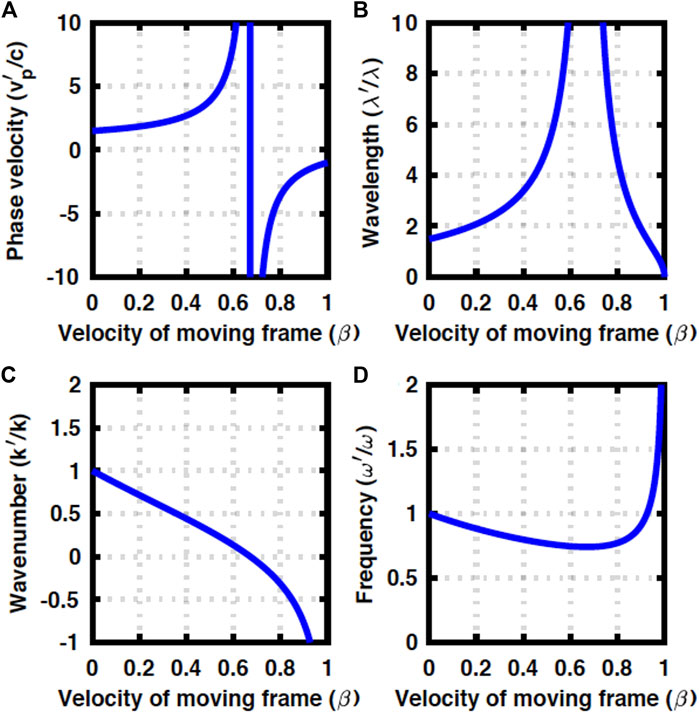
FIGURE 3. Doppler effects in a GRIN fibre at Δ = 0.4ℏω. (A) Phase velocity diverges and it could be larger than c. (B) Wavelength also diverges. (C) Wavenumber changes sign, while (D) frequency is always positive.

The maximum energy gap is Δ = 0.5ℏω, where we cannot expect any propagation along z, and the optical mode is trapped solely in the direction perpendicular to the fibre. Close to this limit, we assumed Δ = 0.49ℏω, and the results are shown in Figure 4. $v_p^{\prime }$ changes its sign even at the smaller β, as expected for the limited kinetic energy.

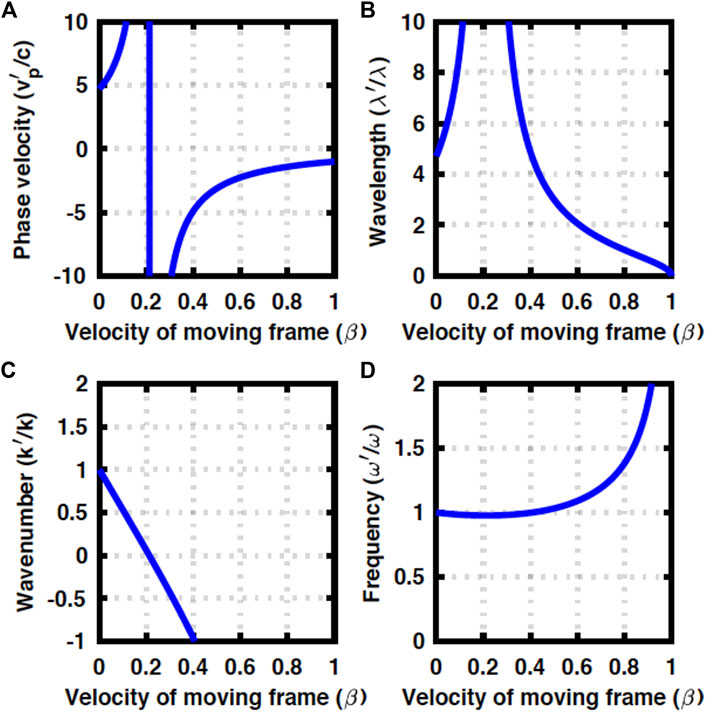
FIGURE 4. Doppler effects in a GRIN fibre at Δ = 0.49ℏω. (A) Phase velocity, (B) wavelength, (C) wavenumber, and (D) frequency. The contributions from orbital degrees of freedom are dominated by the kinetic energy along the fibre.

Regardless of the anomalous phase velocity of $|v_p^{\prime }|$, exceeding c (Figures 3A, 4A), this does not mean the violation of the relativity at all, because the optical communication is determined by the group velocity, defined by

As shown in Figure 5, $|v_{\text{g}}^{\prime }|$ is always smaller than c, such that optical communication beyond c is strictly prohibited. The critical velocity of β to change the sign of $v_{\text{g}}^{\prime }$ does not necessarily coincide with the velocity of β to change the sign of $v_{\text{p}}^{\prime }$.

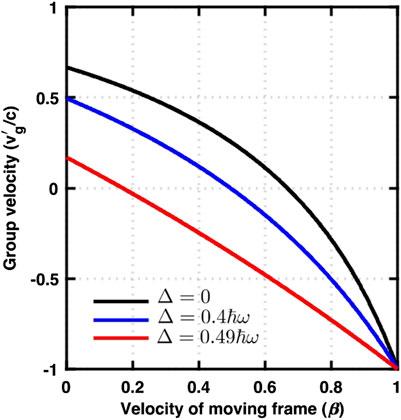
FIGURE 5. The group velocity of light in a GRIN fibre for Δ = 0 (uniform material without confinement), Δ = 0.4ℏω, and Δ = 0.49ℏω (strong confinement in the core). In all cases, the group velocity is less than the speed of light in a vacuum, satisfying the causality.

3.3 Impacts on polarisation states

Finally, we discuss the implications of our considerations for understanding the polarisation states of photons. Before discussing the application of the general theory of relativity to the GRIN fibre, we need to clarify the definition of the polarisation states, because the direction of the apparent propagation changes in the frame moving faster than the phase velocity of the light in the rest frame.

3.3.1 Lights propagating in opposite directions

We clarify the definition of the polarisation states [14], in particular, the direction of the rotation in (Figure 6). There are a lot of different choices of conventions [4, 5, 14, 20, 21], and any notation is acceptable as far as it is used consistently. We prefer to define the polarisation state, seen from the detector side because it is straightforward to describe the motion of the phase front in a standard right-handed (x, y, z) coordinate (Figure 6). We assume that the plane wave of the form e^ikz−iωt is propagating along the +z direction (Figure 7A), and the principal axis (S₃) of the polarisation state is locked along the direction of the propagation [14]. In our definition, the left-circular-polarised state (|L⟩) is located at S₃ = +1 in the normalised Poincaré sphere, while the right-circular-polarised state (|R⟩) is located at S₃ = −1 (Figure 7E). These states are mirror images of each other, and in fact, a mirror can change the circular polarised states to the opposite ones [5, 14, 20, 21].

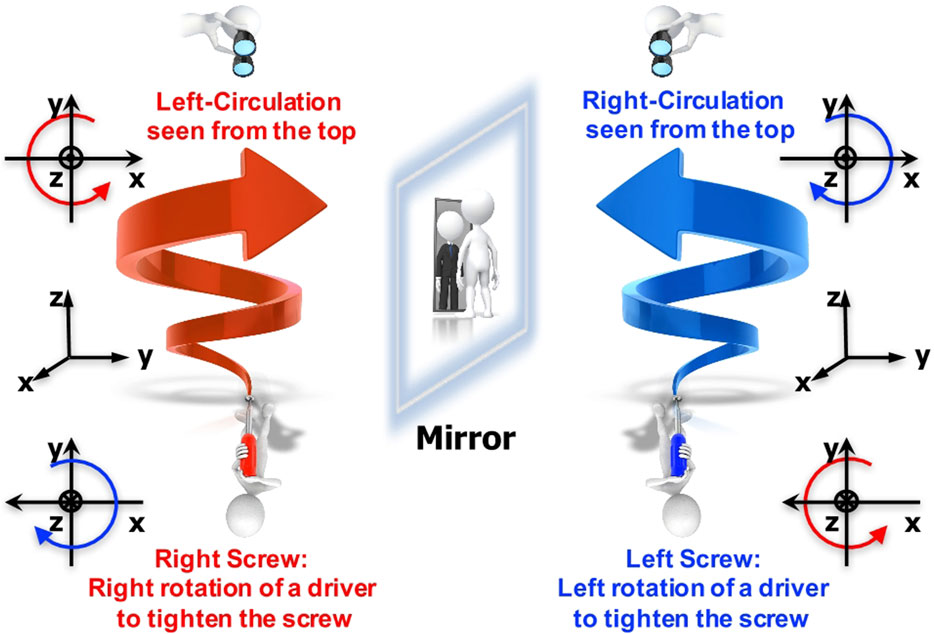
FIGURE 6. Impacts of a mirror. Polarisation states are defined by the motion of the phase front, seen from the top of the light at the detector side. The left-circular-polarised state is characterised by anti-clockwise rotation, while the right-circular-polarised state exhibits clockwise rotation. A mirror exchanges these circularly polarised states to the opposite of each other. Some researchers prefer to define by the motion of the phase front, seen from the source side similar to the definitions of right and left screws. We will not take the latter notation, and follow the mathematical notation to see the right-handed (x, y, z) coordinate to see from the top of the +z-axis.

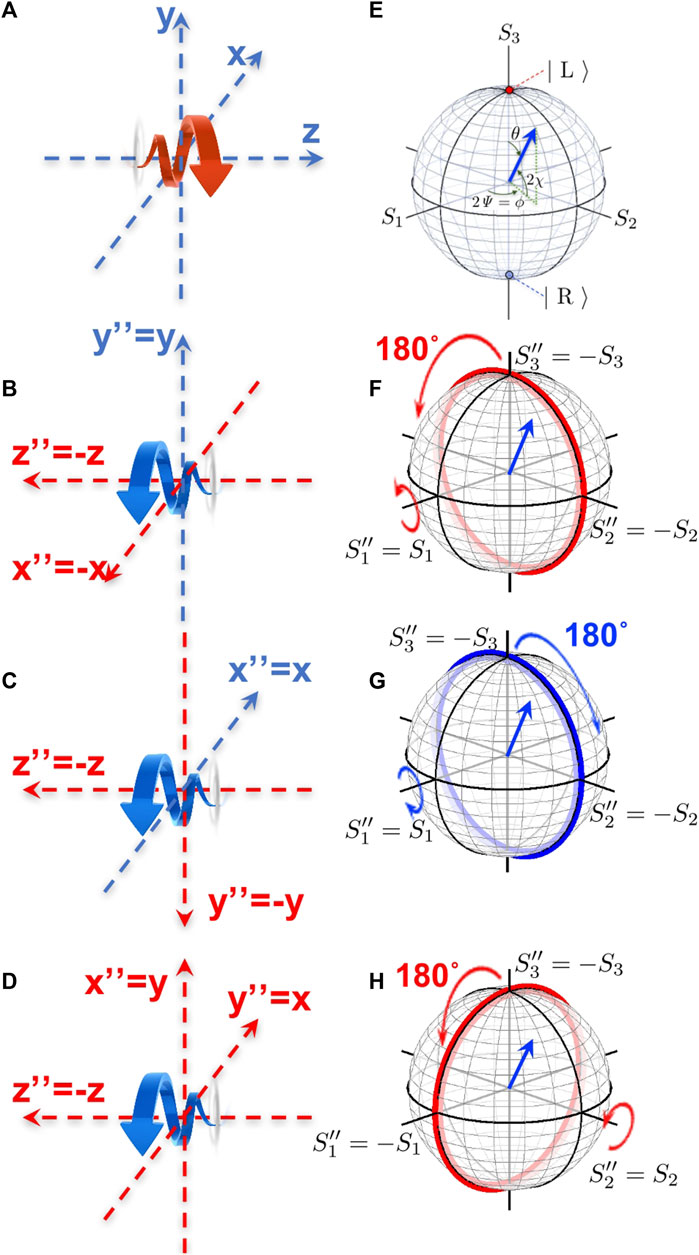
FIGURE 7. Choices of frames and polarisation states. (A) The original frame of (x, y, z) for the light propagating along the +z direction, and (E) the corresponding Poincaé sphere. (B–D) The frames of (x′′, y′′, z′′) for the light propagating along the z′′ = −z direction, and (F–H) the corresponding Poincaé spheres and their relevance to the original Poincaré sphere. Here, all frames are at rest against others. (B) (x′′, y′′, z′′) was made by the rotation along y, which is equivalent to rotate π along S₁ (F). (C) (x′′, y′′, z′′) was made by the rotation along x, which is equivalent to rotate −π along S₁ (G). (D) (x′′, y′′, z′′) was made by the subsequent rotation π from (B), or equivalently by the rotation of −π from (C), which is equivalent to rotate π along S₂ (H).

We consider how we should describe the polarisation states for the light propagating to the opposite direction (Figure 7), since we encountered in the previous section the situation that the moving frame can go faster than the speed of the light in a material, for which the light is seen to go backward. The situation is similar to considering the reflection from a mirror (Figure 6), since a mirror changes the direction of propagation as well as the polarisation state. For example, we consider the left-circular-polarised light propagating along +z direction (Figure 7A), which is characterised by S₃ = +1 (Figure 7E). We consider this light to be reflected backward without changing the rotation of the phase front (Figure 7B), while the direction of the propagation is opposite (−z). If we remain observing the phase front, seen from the +z direction, the circulation is unaffected as the anti-clockwise rotation. However, we defined that the polarisation state must be identified from the detector side, which is the −z direction (Figure 7B). Thus, we define a new frame of (x′′, y′′, z′′), assuming z′′ = −z to clarify the polarisation state. The reflected light propagating along z′′ = −z is now circulating to the clock-wise direction, seen from the +z′′ direction, thus it should be described by the right-circular-polarised state with $S_3^{\prime \prime }=-1$ (Figure 7F). Considering the opposite direction of the propagation, it is natural to assign $S_3^{\prime \prime }=-S_3$, if we would like to keep using the original axes for Stokes parameters. Here, we still have the freedom to choose the relative phase of axes (Figures 7B–D) to the original one (Figure 7A). These choices correspond to how to rotate the original Poincaré sphere at the angle of π (Figure 7F–H). The rotation of the polarisation state is described by a rotation operator in SU(2) Lie algebra [4, 5, 18–21, 59, 60]. If we use the chiral LR-basis, the rotation operator becomes.

where n is the unit vector for the rotational axis, σ = (σ₁, σ₂, σ₃) are Pauli matrices, and Δδ is the angle of the rotation. For example, the rotation along S₁ for π (Figure 7F) is given by

while the opposite rotation for Figure 7G is described by

Similarly, the rotation along S₂ for π (Figure 7H) is given by

These rotations are connected to each other. For example, the coordinate of Figure 7D is realised by rotating Figure 7B for π/2, which correspond to the π rotation along S₃ [15],

In fact, we confirm

Similarly, we can rotate the coordinate of Figure 7C for π/2, which correspond to the −π rotation along S₃, and we confirm

The arbitrary degree of freedom to choose the (x′′, y′′) axes is not restricted to the reflected beam. For example, if we have a linear diagonally polarised state, which is described by S₂ = 1, by changing the definition of the x-axis by rotating 45°, it can also be regarded as the horizontally polarised state of S₁ = 1. Therefore, the difference of the apparent polarisation states between S₁ and S₂ simply depends on the choice of the frame.

Among various arbitrary choices of the frame for the reflected light (Figures 7B–D7), however, one of the most sensible choices would be that of Figure 7D. In this case, the impact of the frame exchange is similar to the unitary transformation by the mirror operation of

whose impact on the spin operators would be

where * is the complex conjugate and ^† is the Hermite conjugate, which involves the transpose of the matrix in addition to the complex conjugate. In this convention, we understand that the polarisation state for the light propagating in the opposite direction of −z is described by the complex conjugate representation of the Lie algebra [61, 62] in the original frame as

which is consistent with Figure 7H. The complex conjugate representation also satisfies the same commutation and anti-commutation relationships with those of the original Pauli matrices [61, 62], such that we confirmed the duality of representations. Therefore, if we would like to keep working in the original frame of (x, y, z) for the light propagating in the opposite direction, we should use the complex conjugate of the spin operators, defined by

where the spinor representation of the creation and annihilation field operators are.

using the creation and annihilation operators of $a_{\mathrm{\sigma }}^{†}$ and a_σ for photons in the polarisation states of left- (σ = L) and right- (σ = R) polarised states, respectively.

3.3.2 Polarisation states observed from a moving frame

Now, we are ready to discuss the polarisation state of light, seen from an observer in the frame of (x′, y′, z′) moving as fast as the phase velocity of light in the rest frame of (x, y, z), where the fibre optic material is placed. We consider that the frame of (x′′ = y′, y′′ = x′, z′′ = −z′) is at rest against the frame of (x′, y′, z′).

First, we consider the weak coupling limit of Δ → 0, which corresponds to a uniform material with the refractive index of n₀. The wavenumber of k′ is always positive, such that the momentum of p′ = ℏk′ is always pointing towards the positive +z′ direction (Figure 1C). On the other hand, ω′ changes its sign as β is increased (Figure 1D), leading to the change of the sign in $v_p^{\prime }$ for v_p < v_z. Suppose that the light at the left-circularly-polarised state (S₃ = 1) in the original frame is propagating along +z. As far as the velocity of the frame is small, v_z < v_p, the polarisation state, seen from the frame of (x′, y′, z′) is not affected, and we obtain $S_3^{\prime }=1$ and the light is seen to be rotating in the anti-clockwise direction, seen from +z′. At v_p < v_z, the light is seen to be propagating along −z′, such that the polarisation state should be examined from the frame of (x′′, y′′, z′′), where the light is propagating along the positive +z′′ direction. The rotation of the phase front, seen from +z′′ direction, is anti-clock-wise due to the negative ω′ < 0 and the observation from the opposite side from the original frame of (x, y, z). Thus, we conclude $S_3^{\prime \prime }=1$, such that the light is still in the left-circular-polarised state. If we consider the complex conjugate relationship between the frames of (x′, y′, z′) and (x′′, y′′, z′′), we obtain $S_3^{\prime }=-S_3^{\prime \prime }=-1$, such that the apparent spin expectation value of S′ depends on the relative velocity of the frame, as is similar to frame-dependent momentum (p′) and energy (E′) governed by Lorentz transformation. For the linearly polarised states, we do not have to be careful too much about the direction of the oscillations, changed by the sign of ω′, because the rotation of the phase front is not involved. However, the description of the polarisation state depends on the choice of the frame (Figures 7B–D). Assume that we have chosen our preferential frame of Figure 7D and we consider the linear-horizontally-polarised state of S₁ = 1 in the original frame of (x, y, z). For v_z < v_p, the polarisation state is not affected, such that we expect $S_1^{\prime }=1$, while for v_p < v_z, we should use the frame of (x′′, y′′, z′′) and the direction of oscillation is considered to be y′′ = x′. Therefore, we conclude that the polarisation state becomes $S_1^{\prime \prime }=-1$, which is a vertically polarised state. This is merely coming from the choice of the frame, and if we convert it to the frame of (x′, y′, z′), we obtain $S_1^{\prime }=-S_1^{\prime \prime }=1$, which has not been changed upon increasing β. We can consider a more complicated polarisation state, but the argument is straightforward.

Next, we consider the polarisation state in a GRIN fibre. As far as the confinement is weak (Figure 2), the qualitative situation is the same as that for a uniform material, discussed above. Therefore, we focus on the strong coupling limit (Figure 3, 4), where k′ changes the sign upon increasing β (Figures 3C, 4C), while ω′ is always positive (Figures 3D, 4D). In these cases, the direction of the rotation of the polarisation state will not be changed by ω′, while we must judge the polarisation state seen from the direction of the propagation, which is changed. Suppose we are considering the light of the left-circularly-polarised state propagating +z direction in the frame of (x, y, z), such that the original state is S₃ = 1. In the frame of (x′, y′, z′), the direction of the propagation could be changed for $v_p^{\prime }<0$, and the polarisation state is examined from z′′. In this case, the phase front is seen to be rotating along the clock-wise-direction, because it is observed from the opposite side of the original frame of z and ω′ is always positive. Thus, we conclude $S_3^{\prime \prime }=-1$ and the light is in the right-circularly-polarised state. This corresponds to $S_3^{\prime }=-S_3^{\prime \prime }=1$, and such that the magnetic spin angular momentum along the principal axis seems to be preserved in spite of the large β, if the mode confinement is very strong. The argument for the linearly polarised state is not altered by the confinement, because it is mainly affected by the choice of the frames, and the sign of ω′ cannot change the direction of the polarisation, although it affects to the direction of the propagation.

In the present work, we assumed that there is no interaction between spin and orbital angular momentum in the GRIN fibre [16]. Therefore, the Doppler effects, discussed in this paper, were not coming from the impact of the spin-orbit interaction. It will be interesting to explore how the Doppler effects are modified in the presence of the spin-orbit interaction [63, 64].

3.3.3 Polarisation states at a rest frame

Finally, we would like to briefly discuss the polarisation state for a photon at a rest frame. As we have discussed above, the moving frame could move faster at the speed of the light in a material. In the GRIN fibre, for example, $v_{\text{g}}^{\prime }$ could be 0 at sufficiently large β (Figure 5). At the rest frame, the light is not seen to be propagating along any direction, such that the transversality condition cannot be imposed. In this case, the light can oscillate along all 3 spatial directions, and the SU(3) symmetry of spin-1 character must be recovered [61, 62, 65, 66]. For SU(3) states, we need 8 generators of rotations, such that we can consider 8-dimensional Gell-Mann parameters to describe the polarisation state, which should be calculated as expectation values of the generator of rotations [66]. Therefore, the polarisation state should be described on the 8-dimensional hypersphere, which we call the Gell-Mann hypersphere [66], instead of the 3-dimensional Poincaré sphere [14, 30, 31].

4 Conclusion

We considered how the light will be seen in a material if an observer is moving as fast as the velocity of the light. As a specific example, we considered a graded index fibre, where the photon dispersion is massive due to the confinement of the orbital, which is quantised both for radial and angular directions. We see that the phase velocity could change the sign, which means that the moving frame can go faster than the speed of light in a material, as evidenced by the Cherenkov radiation [10, 11]. We found a crossover from red-shift to blue-shift as the observer increases the speed beyond the phase velocity. If the optical confinement in the fibre is strong, we found anomalous Doppler effects, with the divergent phase velocity, exceed the speed of light in a vacuum, while the group velocity is always less than c, confirming the causality and the validity of relativity. We have also discussed how the polarisation state is considered in the moving frame, for which the light could be observed to be propagating in the opposite direction from the original frame. We established that the spin operators for the light propagating in the opposite direction are described by the complex conjugate of the original spin operators, which shows the duality of the representations in SU(2) Lie algebra [61, 62]. We are not proposing to confirm this thought experiment in reality, even though it might be possible. Instead, we think our consideration might be useful as a thought-experimental platform for challenging the long-term mystery of what is a photon, imposed by Einstein [1–3].

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work is supported by JSPS KAKENHI Grant Number JP 18K19958.

Acknowledgments

The author would like to express sincere thanks to Prof. I. Tomita and Prof. S. Kurihara for continuous discussions and encouragement.

Conflict of interest

SS is employed by Hitachi, Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References