M2 factor for evaluating fiber lasers from large mode area few-mode fibers

Tao, Rumao; Huang, Long; Li, Min; Shen, Benjian; Feng, Xi; Xie, Lianghua; Weng, Jin; Zhi, Dong

doi:10.3389/fphy.2023.1082086

ORIGINAL RESEARCH article

Front. Phys., 22 February 2023
Sec. Optics and Photonics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1082086

M² factor for evaluating fiber lasers from large mode area few-mode fibers

Rumao Tao¹ www.frontiersin.org

Long Huang² www.frontiersin.org

Min Li¹

Benjian Shen¹ www.frontiersin.org

Xi Feng¹

Lianghua Xie¹ www.frontiersin.org

Jin Weng¹

Dong Zhi²*

¹Laser Fusion Research Center, China Academy of Engineering Physics, Mianyang, China
²Hypervelocity Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang, China

Evaluating the laser quality accurately is one of the most important and fundamental physical issues for laser sources, and the beam quality of lasers from the large mode area few-mode fibers have been haunted by the presence of high order mode for many years. This paper presents a modification to the M² factor, which can be used to evaluate the mode content of fiber lasers accurately and efficiently, no matter whether the fiber modes are superposited coherently or incoherently. By mathematical derivation, the origin of the influence of relative phase on the M² factor has been determined mathematically. A modification to the second moment of the beam intensity profile has been proposed, which eliminates the impact of uncontrollable relative phase on the second moment, and subsequently restores the one-to-one mapping between mode content and M² factor even for coherent superposition cases. Also presented are the results of numerical simulations, which support the validity of the modified M² factor to evaluate the mode content of the high power fiber lasers. With modified M² factor being less than 1.1, the power fraction of LP₁₁ mode content is unique and determined to be less than 3%.

1 Introduction

Narrow Linewidth fiber laser systems, which have earned a solid reputation as a highly power scalable laser with excellent beam quality, are attractive sources for many applications, such as coherent lidar systems, nonlinear frequency conversion, and coherent/spectral beam combining architectures [1–4]. As the output power of fiber lasers grows into the multi-hundred range, detrimental nonlinear effects such as the stimulated Brillouin scattering (SBS) and the self-phase modulation (SPM) become the major limit factors that preclude further power upscaling [5]. Low numerical aperture (NA), large mode area (LMA) step index fiber designs, which support only a few modes in the core, have been employed to overcome the limitation of the nonlinear effects while maintaining a high beam quality of the output laser [6–10]. Various coiling of the fibers have been employed to filter the high order modes and achieve single mode (SM) operation in few-mode fiber [11–16], where criteria are required to evaluate the performance of these coiling tactic. After the introduce of M²-factor, the M²-factor has now become a indispensable standard of the laser beam quality in the fiber laser research and development, and the measured M²-factor is nearly always specified to evaluate the fundamental mode (LP₀₁) purity whenever a new fiber laser source is demonstrated or produced. The M²-factor is generally used to evaluate the fundamental mode purity in the aforementioned tactic of achieving SM operation in LMA fibers [11–16], and low M² values have been taken to imply that the near-SM or near-diffraction-limited performance is achieved: lower M² values means higher fraction of fundamental mode content in LMA fibers. Although the M² values of the fundamental mode is about 1, it does not means that the laser contains more fundamental mode power by M² →1. In LMA fiber, the high order mode, especially LP₁₁ mode, is hard to be eliminated completely [18, 19]. Coiling-induced bend loss increases with the order of the fiber mode, and the bend loss of LP₁₁ mode is the lowest among the high order mode. Meanwhile, the fiber perturbations result in that the high order modes are continually repopulated due to coupling between the fundamental mode and the high order modes [17], which is the strongest for the LP₁₁ mode. In the presence of LP₁₁ mode, even the excellent beam quality (M² < 1.1) in LMA fibers does not guarantee low power fraction of LP₁₁ mode when the modes are superposited coherently, which are generally true for the narrow linewidth fiber lasers [18]. Due to the presence of the relative phase between the fiber modes, there is no one-to-one mapping between the mode content and the M²-factor for the coherent superposition cases [18, 20]. For certain superposition state in LMA fibers, the M² value can be as good as 1.08 for a fiber laser consists of 30% LP₁₁ and 70% LP₀₁ [18], which results in that the widely employed criteria is unable to evaluate the fiber laser mode purity performance, and limits the applications of high power fiber lasers in the cases requiring strict mode purity. To determine the fundamental mode content, sophisticated methods should be employed, such as spatially and spectrally resolved imaging, cross-correlated imaging, modal decomposition [21–25]. However, the aforementioned methods require specially designed experimental setups and complicated algorithms, and are not compatible with the standard measuring instruments in laser industry [26, 27]. In recent years, some intelligent methods have been introduced to calculate the M²-factor [28–30], which is still suffered from the problem induced by the presence of high order modes. A modification to the present method is simple and compatible with the standard measuring instruments, which inspires the work in this manuscript.

In this manuscript, the term that leads to the variation of the M² factor has been determined, and a modification to M² factor has been proposed to evaluate the beam quality or mode content of high power narrow linewidth laser from the LMA low NA step index fibers, which can mitigate the dependence of M² factor on the uncontrollable relative phase between the LP₀₁ and LP₁₁ modes, and restores the one-to-one mapping between the mode content and the M²-factor for coherent superposition cases. Numerical simulations have been carried out to validate the modified M² factor, which revealed that the modified M² factor can be used to evaluate the mode content of fiber lasers, no matter whether the modes are superposited coherently or incoherently.

2 Theoretical model

As pointed out in [18, 19], for low NA, LMA fiber, LP₁₁ mode is hard to be stripped totally and is the most problematic. In the following analysis, we focus our attention mainly on the case that only LP₁₁ mode is contained in the laser, and the electric field of the high power fiber laser for narrow linewidth fiber laser can be expressed as [17]:

E (x, y, 0) = \sqrt{1 - P_{11}} Ψ_{L P_{01}} (x, y, 0) + \sqrt{P_{11}} e^{i Δ ϕ_{11}} Ψ_{L P_{11}} (x, y, 0), (1)

where P₁₁ is the power in the LP₁₁ mode, and △ϕ₁₁ is the relative phase between the LP₁₁ mode and the LP₀₁ mode, which drift with fluctuations in temperature and other environmental factors, and are difficult to reliably control. In step index fibers, the normalized electric field of LP₁₁ mode ψ_LPmn(x, y, z = 0) can be written as:

Ψ_{L P_{m n}} (x, y, 0) = \frac{f_{m n} (r)}{\sqrt{N_{m n}}} \cos (m ϕ), (2)

with

f_{m n} (r) = \frac{J_{m} (U_{m n} r / a)}{J_{m} (U_{m n})} a \geq r > 0, (3a)

f_{m n} (r) = \frac{K_{m} (W_{m n} r / a)}{K_{m} (W_{m n})} r > a, (3b)

where J_m and K_m is the Bessel function of the first kind and the modified Bessel function of the second kind, respectively, a is the core radius of the fiber, (r = √x²+y², ϕ) is polar coordinates and λ is the wavelength. U_mn and W_mn are defined as in [31], and N_mn is the normalization factor, which can be expressed by:

N_{0 n} = 2 π \int_{0}^{\infty} f_{0 n}^{2} (r) r d r f o r m = 0, (4a)

N_{m n} = π \int_{0}^{\infty} f_{m n}^{2} (r) r d r f o r m > 0 . (4b)

According to Eq. 1, the intensity of the near field is given by:

\begin{array}{l} I (x, y, 0) = P_{01} Ψ_{L P_{01}}^{2} (x, y, 0) + P_{11} Ψ_{L P_{11}}^{2} (x, y, 0) \\ + 2 \sqrt{P_{01} P_{11}} Ψ_{L P_{01}} (x, y, 0) Ψ_{L P_{11}} (x, y, 0) \cos Δ ϕ_{11}, \end{array} (5)

and the intensity of the field after propagating a distance of z is given by:

\begin{array}{l} I (x, y, z) = P_{01} Ψ_{L P_{01}}^{2} (x, y, z) + P_{11} Ψ_{L P_{11}}^{2} (x, y, z) \\ + \sqrt{P_{01} P_{11}} Ψ_{L P_{01}}^{*} (x, y, z) Ψ_{L P_{11}} (x, y, z) e^{i Δ ϕ_{11}} \\ + \sqrt{P_{01} P_{11}} Ψ_{L P_{01}} (x, y, z) Ψ_{L P_{11}}^{*} (x, y, z) e^{- i Δ ϕ_{11},} \end{array} (6)

where Ψ_LPmn(x, y, z) is the field after Ψ_LPmn(x, y, 0) propagates a distance of z. Then the M² factor is calculated by [32]:

M_{x}^{2} = (\frac{π w_{0 x}}{λ z}) \sqrt{w_{z x}^{2} - w_{0 x}^{2}}, (7a)

M_{y}^{2} = (\frac{π w_{0 y}}{λ z}) \sqrt{w_{z y}^{2} - w_{0 y}^{2},} (7b)

with

w_{z x} = 2 σ_{z x}, w_{z y} = 2 σ_{z y}, (8a)

σ_{z x}^{2} = \frac{\int {(x - x_{0} (z))}^{2} I (x, y, z) d x d y}{\int I (x, y, z) d x d y}, (8b)

σ_{z y}^{2} = \frac{\int {(y - y_{0} (z))}^{2} I (x, y, z) d x d y}{\int I (x, y, z) d x d y}, (8c)

w_{0 x} = 2 σ_{0 x}, w_{0 y} = 2 σ_{0 y}, (8d)

σ_{0 x}^{2} = \frac{\int {(x - x_{0} (0))}^{2} I (x, y, 0) d x d y}{\int I (x, y, 0) d x d y}, (8e)

σ_{0 y}^{2} = \frac{\int {(y - y_{0} (0))}^{2} I (x, y, 0) d x d y}{\int I (x, y, 0) d x d y}, (8f)

where σ_zx(y) and w_zx(y) is the second moment of the beam intensity profile and the beam size at the distance of z along x(y) direction, respectively, which is σ_0x(y) and w_0x(y) at the near filed. (x₀(z), y₀(z)) is the gravity center of the beam at the distance of z, given by:

x_{0} = \frac{\int x I d x d y}{\int I d x d y}, (9a)

y_{0} = \frac{\int y I d x d y}{\int I d x d y}, (9b)

where I is the laser intensity at arbitrary distance. In Eq. 7a, one can see that the M² seems to be dependent on the wavelength. However, the w_zx(y) is also related to the wavelength through the laser intensity I. In fiber waveguide, the variation of the wavelength changes the V-number, which results in the laser intensity I changes. It is shown that the M² sharply peaks near the corresponding cutoff values of the V-number but remains nearly constant for V>3 [20]. In the practical high power laser systems, the V is generally larger than 3, so the dependence of M² on wavelength is negligible. The divergence angle of the beam can be obtained directly from M² value by employing the simple Equation in [33].

The second moment of the beam intensity profile can be expressed as:

σ_{z x}^{2} = \frac{\int x^{2} I d x d y}{\int I d x d y} + \frac{x_{0}^{2} \int I d x d y}{\int I d x d y} - 2 \frac{x_{0} \int x I d x d y}{\int I d x d y}, (10a)

σ_{z y}^{2} = \frac{\int y^{2} I d x d y}{\int I d x d y} + \frac{y_{0}^{2} \int I d x d y}{\int I d x d y} - 2 \frac{y_{0} \int y I d x d y}{\int I d x d y}, (10b)

According to the electric field distribution of the LP₀₁ mode and the LP₁₁ mode, we can obtain:

Ψ_{L P_{01}} (- x, y, 0) = Ψ_{L P_{01}} (x, y, 0), (11)

and

Ψ_{L P_{11}} (x, y, 0) = - Ψ_{L P_{11}} (- x, y, 0), (12)

where the LP₁₁ mode is assumed to be anti-symmetric along x direction.

By using the extended Huygens–Fresnel principle [34–38], the electric field of the modes at the z plane can be expressed as:

\begin{array}{l} Ψ_{L P_{01}} (p, q, z) = \\ \frac{k}{2 π z} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} Ψ_{L P_{01}} (x, y, 0) \exp \{\frac{i k}{2 z} [{(p - x)}^{2} + {(q - y)}^{2}]\} d x d y, \end{array} (13a)

\begin{array}{l} Ψ_{L P_{11}} (p, q, z) = \\ \frac{k}{2 π z} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} Ψ_{L P_{11}} (x, y, 0) \exp \{\frac{i k}{2 z} [{(p - x)}^{2} + {(q - y)}^{2}]\} d x d y, \end{array} (13b)

where (p, q) is the coordinate at the z plane. Then we can derive:

\begin{array}{l} Ψ_{L P_{01}} (- p, q, z) \\ = \frac{k}{2 π z} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} Ψ_{L P_{01}} (x, y, 0) \exp \{\frac{i k}{2 z} [{(- p - x)}^{2} + {(q - y)}^{2}]\} d x d y \\ \overset{ξ = - x}{=} - \frac{k}{2 π z} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} Ψ_{L P_{01}} (- ξ, y, 0) \exp \{\frac{i k}{2 z} [{(- p + ξ)}^{2} + {(q - y)}^{2}]\} d ξ d y, \end{array} (14a)

\begin{array}{l} Ψ_{L P_{11}} (- p, q, z) \\ = \frac{k}{2 π z} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} Ψ_{L P_{11}} (x, y, 0) \exp \{\frac{i k}{2 z} [{(- p - x)}^{2} + {(q - y)}^{2}]\} d x d y \\ \overset{ξ = - x}{=} - \frac{k}{2 π z} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} Ψ_{L P_{11}} (- ξ, y, 0) \exp \{\frac{i k}{2 z} [{(- p + ξ)}^{2} + {(q - y)}^{2}]\} d ξ d y, \end{array} (14b)

Take Eqs 11, 12 into consideration, the above equations can be rewritten as:

\begin{array}{l} Ψ_{L P_{01}} (- p, q, z) \\ = - \frac{k}{2 π z} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} Ψ_{L P_{01}} (ξ, y, 0) \exp \{\frac{i k}{2 z} [{(p - ξ)}^{2} + {(q - y)}^{2}]\} d ξ d y, \end{array} (15a)

\begin{array}{l} Ψ_{L P_{11}} (- p, q, z) \\ = \frac{k}{2 π z} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} Ψ_{L P_{11}} (ξ, y, 0) \exp \{\frac{i k}{2 z} [{(p - ξ)}^{2} + {(q - y)}^{2}]\} d ξ d y, \end{array} (15b)

which can be simplified into:

Ψ_{L P_{01}} (- p, q, z) = - Ψ_{L P_{01}} (p, q, z), (16)

and

Ψ_{L P_{11}} (- p, q, z) = Ψ_{L P_{11}} (p, q, z), (17)

Referring to the odd-even property, we can obtain:

\int \int Ψ_{L P_{01}}^{*} (x, y, z) Ψ_{L P_{11}} (x, y, z) d x d y = 0, (18a)

\int \int Ψ_{L P_{01}} (x, y, z) Ψ_{L P_{11}}^{*} (x, y, z) d x d y = 0, (18b)

\int \int x Ψ_{L P_{01}}^{*} (x, y, z) Ψ_{L P_{11}} (x, y, z) d x d y \neq 0, (18c)

\int \int x Ψ_{L P_{01}} (x, y, z) Ψ_{L P_{11}}^{*} (x, y, z) d x d y \neq 0, (18d)

\int \int x^{2} Ψ_{L P_{01}}^{*} (x, y, z) Ψ_{L P_{11}} (x, y, z) d x d y = 0, (18e)

\int \int x^{2} Ψ_{L P_{01}} (x, y, z) Ψ_{L P_{11}}^{*} (x, y, z) d x d y = 0, (18f)

According to Eq. 18a, one can conclude that only the third term in Eq. 10a is non-zero, which means that the third term introduces the effect of relative phase on the final obtained beam quality value. If we rewritten Eq. 10b as:

σ_{z x}^{2} = \frac{\int x^{2} I d x d y}{\int I d x d y}, (19a)

σ_{z y}^{2} = \frac{\int y^{2} I d x d y}{\int I d x d y}, (19b)

Eq. 7b becomes independent of the relative phase. Replacing the calculation equation of the second moment Eq. 10a with Eq. 19a, the calculated M² factor is only dependent on the power content of LP₁₁ mode, and the influence of relative phase on the M² factor is eliminated. By employing Eq. 19b, the influence of the last two terms in Eqs 5, 6, representing the mode interference, disappears, and the remaining terms is the same as the incoherent case. For the case that the modes are superposited incoherently, the gravity center of the beam is zero, Eq. 10b reduce to the form of Eq. 19a, and the modified M² factor in coherently superposited cases is coincident with those of the classical M² factor in incoherently superposited cases, which means that the ideal value for the modified M² factor is still very close to 1. In conclusion, the modified M² factor calculated from Eqs 7a, 19b can be used to evaluate the high power narrow linewidth fiber lasers.

3 Numerical simulations

For high power fiber lasers, nonlinear effects are the main limitation for power scaling, which is stronger for higher laser intensity [39]. Generally, fibers with larger core diameter have been employed to reduce the laser intensity in fiber core. However, the number of the supported modes in the core increases as the core diameter increases, which renders the fiber lasers into multimode operation, and undermines the beam quality [40]. To realize high power laser while maintaining near diffraction limited beam quality, a core diameter of 30 μm is generally used [41–47]. So the exemplary fiber that will be considered here has an ideal step-index profile with a 30 μm core and a core NA of 0.065, which was chosen to be representative of a commercially-available LMA fiber and to validate the analysis in the former section. For high power narrow linewidth fiber lasers, the wavelength is generally located at 1064nm, and the laser wavelength used in simulation is chosen to be 1064 nm. The bend loss as a function of the bend radius for different modes is shown in Figure 1, which is calculated using the method of Marcuse [48]. An additional correction factor, yielding an effective bending diameter, has been employed to incorporate the material stress-optic effect [49]. It shows that even with the bend radius of 10cm, the bend loss for LP₂₁ mode is significantly large, which is about 100 dB/m, which means that higher order mode can be stripped efficiently by coiling the fibers. For common fiber laser package of low NA LMA step index fiber, the bend radius of fiber is not larger than 10 cm to mitigating mode instability [6, 14], so it is reasonable to consider only the LP₀₁ and LP₁₁ mode.

FIGURE 1

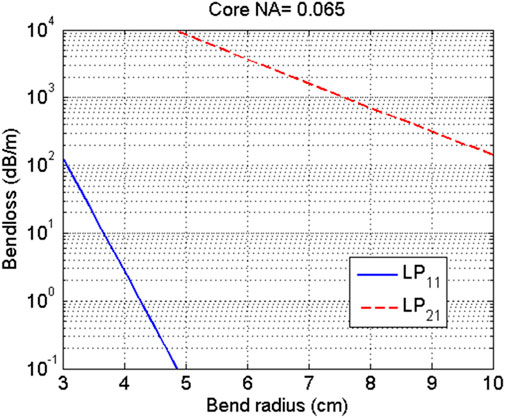
FIGURE 1. Bend loss vs. bend radius for different modes of a 0.065 NA fiber with a 30-μm-core at 1064 nm.

We first calculated the M² factor by using the classical definition. The fiber mode profiles at the fiber output were propagated a distance from the initial plane (z = 0) by using the angular spectrum propagation method, which is based on fast Fourier Transform algorithm [50, 51]. Then several beam parameters of interest, such as second moment of the beam intensity profile and beam gravity centroid, can be calculated directly from the intensity distribution at the initial plane and distant plane, which are used to calculate the M² factor through Eqs 7a, 8a, 8b, 8c. The M² factor (in x and y direction) as a function of the LP₁₁ fraction and the relative phase is calculated, which is shown in Figure 2. It is shown that the value of M² factor is dependent on the LP₁₁ fraction and the relative phase, and M² is less than 1.1 even with the LP₁₁ fraction as high as 0.35. It is indicated in [52] that the power in the bucket is dependent on the LP₁₁ fraction, which means that even M² < 1.1 can not guarantee excellent long-distance propagation properties or high energy concentration for narrow width fiber laser, and that the M² factor can not reflect the mode content and is unsuitable to verify good propagation properties of a LMA fiber.

FIGURE 2

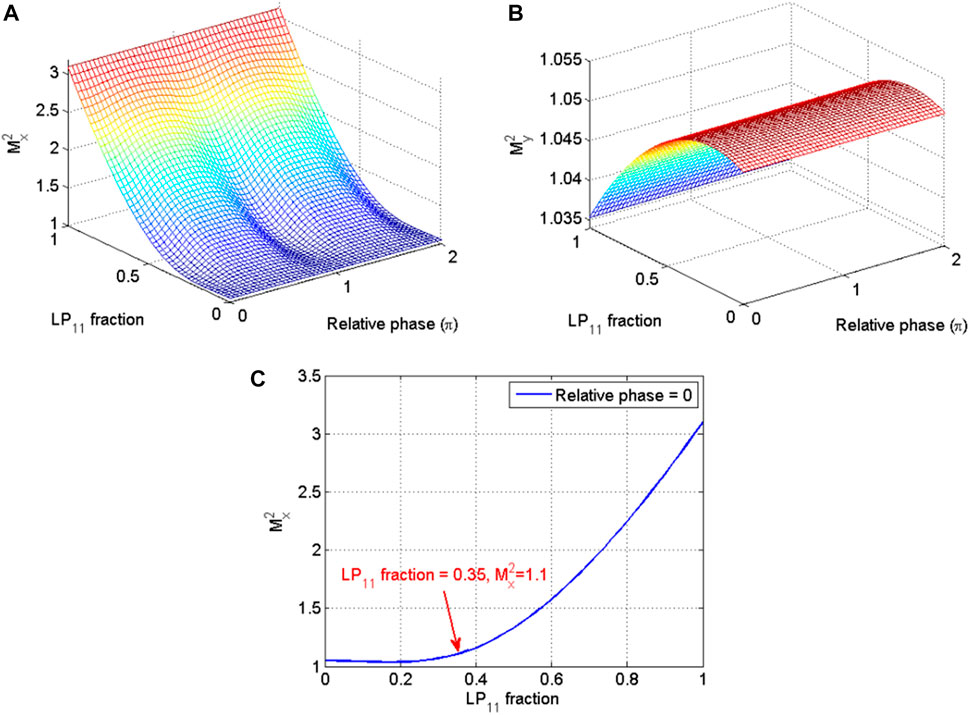
FIGURE 2. M² as a function of LP₁₁ fraction and relative phase for x direction (A) and y direction (B), M² as a function of LP₁₁ fraction for the case that the relative phase is 0 (C).

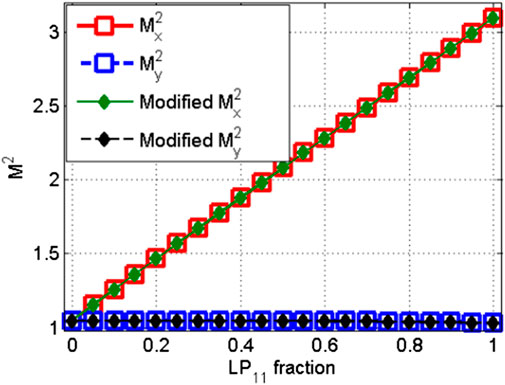
Employing the modified calculation, the modified M² factor as a function of relative phase and power fraction is presented in Figure 3. It can be seen from Figure 3A that the calculated M² factor is independent of the uncontrollable relative phase, which validate the predication in the theoretical analysis in Section 2. It also reveals in Figure 3B that the calculated modified M² factor increases linearly with the increase of high order mode content, which means that the M² factor can be used to evaluate the beam quality or mode content of the laser from low NA, LMA fibers. With modified M² factor being less than 1.1, the power fraction of LP₁₁ mode content is less than 3%. In Figure 3B, the modified M_y² value is constant with a change in the LP₁₁ fraction. This is due to that M² value in the y direction is nearly the same for LP₀₁ mode and LP₁₁ mode [20], and the modified M_y² value is a weighted superposition of the M² value for LP₀₁ mode and LP₁₁ mode.

FIGURE 3

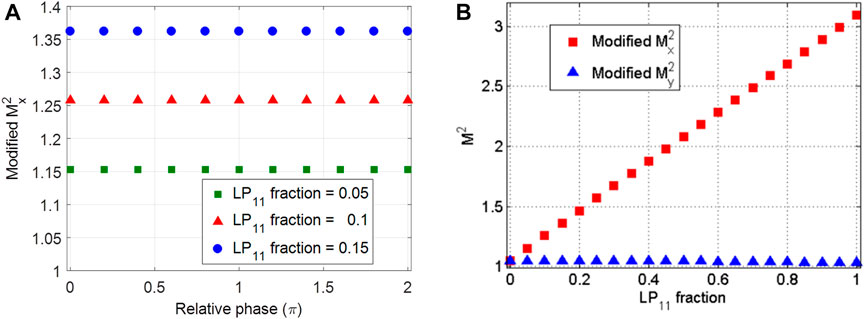
FIGURE 3. Beam quality factor of the coherent mixture of LP₀₁ and LP₁₁ modes, as a function of the relative phase (A) and higher order mode content (B).

The calculated M² factor as a function of power fraction is presented in Figure 4, in which the modes are superposited incoherently for the cases of broadband fiber lasers. Both classical and modified M² factor is used to evaluate the beam quality, which indicates that there is no difference in the two methods for the case that the modes are superposited incoherently. One can conclude that the modified M² factor is suitable for evaluating the beam quality of the fiber laser whenever the modes are superposited coherently or incoherently, which means that the methods can be employed in broader applications, not only restricted to evaluate the narrow linewidth fiber lasers but also the broadband ones. Due to that the modification is only made on the calculation of the second moment of the beam intensity profile, the modified M² can be used in the conventional measuring instrument except for updating the calculating software programs.

FIGURE 4

FIGURE 4. Beam quality factor of the incoherent mixture of LP₀₁ and LP₁₁ modes.

4 Conclusion

We have presented a modification to the M² factor for high power narrow linewidth lasers from low NA, LMA fibers. The modified M² factor eliminates the influence of the uncontrollable relative phase by ignoring the gravity center in the calculation of the beam intensity profile second moment, and the one-to-one mapping between the M² factor and the mode content has been restored, which make the M² factor can be employed to characterize the mode content even for the narrow linewidth fiber lasers. It is demonstrated numerically that the modification to M² factor can reflect the mode content, and the M² factor → 1 means that less high order mode are contained in the laser beam. With the new calculation method, the power fraction of LP₁₁ mode is less than 3% when the modified M² parameter is less than 1.1. The results can be used to improve the method to measure the beam quality of high power fiber lasers.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the study and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) (61905226), and the Youth Talent Climbing Foundation of the Laser Fusion Research Center.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Fu S, Shi W, Feng Y, Zhang L, Yang Z, Xu S, et al. Review of recent progress on single-frequency fiber lasers. J Opt Soc Am B (2017) 34(3):A49–A62. doi:10.1364/josab.34.000a49