Coherence Analysis of Symmetric Star Topology Networks

1 Introduction

Complex networks take the networks topology and the dynamic models of networks nodes as the main research object. With the help of mathematical science and information science, complex networks are widely applied in neural networks, social networks, control theory, and consensus [1–4]. The problem of networks consensus means that networks reach a common decision on a certain issue. It can be quantified by network coherence. Examples of consensus widely exist in real life, such as groups of animals will produce consensus behavior in one direction after being disturbed. The consensus of complex network have many potential applications, such as information control and decision, load balancing [5–7].

Scholars take common networks topology as the main research object, and have achieved abundant theoretical results [8–16]. Y. Yi et al. took Koch Network as the research object to study the first-order coherence of Koch network with leaderless and one leader [8]. M. Dai et al. investigated the first-order coherence of a class of weighted fractal networks, and further analyzed the relationships between iterative parameters and first-order coherence [9]. X. Wang et al. obtained the first-order coherence of 5-rose network and further analyzed the relationships between the first-order coherence and the number of nodes [13]. T. Jing et al. studied the first-order coherence of ring-trees networks and recursive trees, and found that the first-order coherence of ring-trees networks are better than that of recursive trees [16].

As a common computer local area network structure, star topology networks have simple structure and only one central node, which are convenient for management and maintenance, and have strong expansibility. Each node is directly connected to the central node. The fault is easy to detect and isolate, and the faulty nodes can be easily eliminated. They have a wide range of applications in physics, computer and other disciplines [17–19]. S. Jafarizadeh et al. studied the optimization of synchronizability of symmetric star topology networks with different intra-layer coupling strength [20]. S. Patterson et al. studied the consensus dynamics of various networks, including star networks, and obtained the coherence of various networks [21]. J. Chen et al. proposed graph operation method to construct the network models of book graph on the basis of star networks, and analyzed the influence of network internal parameters on its coherence. It is found that the more nodes in the star graph, the better the consensus of the book graph network [22]. D. Huang et al. studied the Laplacian spectrum of several double-layer star-like networks, and analyzed and compared the coherence of these networks [23].

In this paper, the consensus of symmetric star topology networks are studied by using the spectrum theory. The innovations of this paper are as follows:

1. We proposed three new connection modes of symmetric star topology networks with the same number of nodes, which provided a research basis for comparing the coherence of the three networks.

2. According to the topology of three kinds of networks, the corresponding Laplacian characteristic polynomial is obtained, and then the specific expressions of first-order coherence are given.

3. The relationships between the coherence of star networks and parameters are analyzed by numerical simulation. It is found that no matter how the branch length and the number of branches change, only one of the three kinds of network models has the best consensus, and the change of branch length has more effective impact on consensus.

This paper is organized as follows: the preliminaries are given in Section 2. The analytical formula of the first-order coherence of three kinds of symmetric star networks are given in Section 3. Numerical simulation experiments and analysis are given in Section 4. Section 5 gives the conclusion.

2 Preliminaries

2.1 The Laplacian Matrix and Eigenvalue Spectrum of Networks

Let G = (V, E) be a undirected and connected network, where V = {1, 2, 3, … , n − 1, n} is the network vertex set and E = {e₁, e₂, e₃, … , e_m−1, e_m} is the network edge set. The adjacency matrix of the network is denoted as $A={(a_{ij})}_{n\times n}$. When i is connected to j, a_ij = 1, otherwise, a_ij = 0. The degree matrix of the network is written as $W={(w_{ii})}_{n\times n}$, where $w_{ii}={\sum }_{j=1}^n{a}_{ij}$ is the degree of node i. The Laplacian matrix of the network is denoted by L = W − A, and the root of the corresponding characteristic polynomial det(λI − L) is called the Laplacian eigenvalue of the network. According to the semi-positive property of the Laplacian matrix, all eigenvalues λ₁, λ₂, λ₃, … , λ_n−1, λ_n of the matrix are non-negative. Moreover, the multiplicity of the zero eigenvalue of the matrix is the same as the number of connected branches of the network, Therefore, it is assumed that the eigenvalues satisfy 0 = λ₁ < λ₂ ≤ λ₃ ≤ ⋯ ≤ λ_n−1 ≤ λ_n for connected network G.

2.2 The Relationships Among Network Coherence and Laplacian Eigenvalues

The network dynamics model with noise interference is written as follows [21].

L is the Laplacian matrix of the network, σ(t) represents the interference of Gaussian white noise on all nodes of the network at t. In the case of σ(t) = 0, the networks are not interfered by noise, which tends to be consensus at this time. In the case of σ(t) ≠ 0, the network is interfered, which can not be completely consensus and will change around the average value of the network.

Definition 1. The concept of first-order network coherence is the steady-state variance deviating from the average value of all nodes [21].

The first-order coherence of the network can be derived by the non-zero eigenvalues of the Laplacian matrix [21], the specific relationship is as follows:

According to the definition of first-order coherence, the smaller H⁽¹⁾ is, the better the consensus of the network is.

2.3 Compute the Required Lemmas

In order to get the main conclusions of this paper, the following lemmas are given.

Lemma 1. Let the corresponding characteristic polynomial of matrix B_n be F_n(λ) = |λI − B_n| = a_nλⁿ + ⋯ + a₂λ² + a₁λ + a₀,

then a₀ = (−1)ⁿ(n + 1), $a_1={(-1)}^{n-1}\frac{n(n+1)(n+2)}{6}$, $a_2={(-1)}^{n-2}\frac{(n-1)n(n+1)(n+2)(n+3)}{120}$.Proof. According to the relationships among the coefficients of characteristic polynomial and the principal minors of matrix, a₀ = (−1)ⁿ|B_n|, then $a_0={(-1)}^n(n+1){(\frac{2}{2})}^n={(-1)}^n(n+1)$.Just for the sake of proof, let the diagonal elements of matrix B_n be b_ii(1 ≤ i ≤ n), then

When n = 1, a₂ = 0, conclusion is tenable. We assume that n ≤ i, conclusion is tenable. When n = i + 1, F_i+1(λ) = (λ − 2)F_i(λ) − F_i−1(λ). Let F_i(0), F_i(1) and F_i(2) be the constant term, first-order coefficient and quadratic coefficient of the characteristic polynomial of B_i, $F_{i+1}(2)=F_i(1)-2F_i(2)-F_{i-1}(2)={(-1)}^{i-1}\frac{i(i+1)(i+2)(i+3(i+4))}{120}$, conclusion is tenable.

Lemma 2. Let the corresponding characteristic polynomial of matrix C_n be Q_n(λ) = |λI − C_n| = b_nλⁿ + ⋯ + b₂λ² + b₁λ + b₀, where,

then b₀ = (−1)ⁿ, $b_1={(-1)}^{n-1}\frac{n(n+1)}{2}$, $b_2={(-1)}^{n-2}\frac{(n-1)n(n+1)(n+2)}{24}$.Proof. Let Q_i(0), Q_i(1) and Q_i(2) be the constant term, first-order coefficient and quadratic coefficient of the characteristic polynomial of C_i. Q_n(λ) = F_n(λ) + F_n−1(λ), using Lemma 1, b₀ = Q_n(0) = F_n(0) + F_n−1(0) = (−1)ⁿ(n + 1) + (−1)ⁿ⁻¹n = (−1)ⁿ, $b_1=Q_n(1)=F_n(1)+F_{n-1}(1)={(-1)}^{n-1}\frac{n(n+1)(n+2)}{6}+{(-1)}^{n-2}\frac{(n-1)n(n+1)}{6}={(-1)}^{n-1}\frac{n(n+1)}{2}$, $b_2=Q_n(2)=F_n(2)+F_{n-1}(2)={(-1)}^{n-2}\frac{(n-1)n(n+1)(n+2)}{24}$.

3 The First-Order Coherence of Three Kinds of Symmetric Star Topology Networks

3.1 The First-Order Coherence of Symmetric Star Topology Networks S^a(m, n)

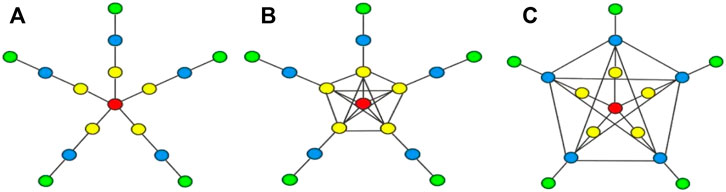
Let the star network with m branches be S^a(m, 1), and appropriately extend its branch length to increase its length from 1 to n form a symmetric star topology network S^a(m, n) [20]. As is shown in Figure 1A.

FIGURE 1. (A) S^a(5, 4), (B) S^b(5, 4), (C) S^c(5, 4).

Let the Laplacian matrix of S^a(m, n) be L¹, the characteristic polynomial is P₁(λ) = |λI − L¹|. |λI − L¹| =

We use elementary row transformation to transform it into the lower triangular determinant,

where ∗ = λ − m − m/p_n(λ), p₁(λ) = λ − 1, p_i(λ) = λ − 2–1/p_i−1(λ) (2 ≤ i ≤ n).

Therefore, $P_1(\lambda )={[H_1(\lambda )]}^{m-1}{J}_1(\lambda )$, where H₁(λ) = p₁(λ)p₂(λ)⋯p_n(λ) = Q_n(λ), J₁(λ) = [(λ − m)Q_n(λ) − mQ_n−1(λ)].

According to the preliminaries, the zero eigenvalue of P₁(λ) appears J₁(λ), let 0 < γ₁ ≤ γ₂ ≤ γ₃ ≤ ⋯ ≤ γ_n be the Laplacian eigenvalues of H₁(λ), 0 = δ₁ ≤ δ₂ ≤ δ₃ ≤ ⋯ ≤ δ_n ≤ δ_n+1 be the Laplacian eigenvalues of J₁(λ).

Theorem 1. The first-order coherence of S^a(m, n) is

Proof. It can be inferred from preliminaries

We first calculate by the Vieta theorem and Lemma 2 [16],

We further calculate ${\sum }_{i=2}^{n+1}\frac{1}{{\delta }_i}$.Let J₁(λ) = c_n+1λⁿ⁺¹ + c_nλⁿ⋯ + c₂λ² + c₁λ, then

We use the Vieta theorem again, ${\sum }_{i=2}^{n+1}\frac{1}{{\delta }_i}=-\frac{c_2}{c_1}$. Because of J₁(λ) = [(λ − m)Q_n(λ) − mQ_n−1(λ)], therefore,

Then,

Therefore,

3.2 The First-Order Coherence of Symmetric Star Topology Networks S^b(m, n)

Consider adding the connection relations of nodes of symmetric star topology networks S^a(m, n). The symmetric star topology networks with fully connected nodes at the second layer are denoted as S^b(m, n). As is shown in Figure 1B.

Let the Laplacian matrix of S^b(m, n) be L², the characteristic polynomial is P₂(λ) = |λI − L²|. |λI − L²| =

where ⊗ = λ − m − 1.

Similar to Theorem 1, $P_2(\lambda )={[H_2(\lambda )]}^{m-1}{J}_2(\lambda )$, where H₂(λ) = (λ − m − 2)Q_n−1(λ) − Q_n−2(λ), J₂(λ) = [(λ² − (m + 2)λ + m)Q_n−1(λ) − (λ − m)Q_n−2(λ)].

The zero eigenvalue of P₂(λ) appears J₂(λ), let 0 < ω₁ ≤ ω₂ ≤ ω₃ ≤ ⋯ ≤ ω_n be the Laplacian eigenvalues of H₂(λ), 0 = ψ₁ ≤ ψ₂ ≤ ψ₃ ≤ ⋯ ≤ ψ_n ≤ ψ_n+1 be the Laplacian eigenvalues of J₂(λ).

Theorem 2. The first-order coherence of S^b(m, n) is.$H^{(1b)}=\frac{1}{2(mn+1)}[\frac{(m-1)[2+(n-1)(mn+n+2)]}{2(m+1)}+\frac{6+3(n-1)(mn+n+2)+m(n-2)(n-1)n}{6(mn+1)}]$.Proof. Similar to Theorem 1,

First, we calculate ${\sum }_{i=1}^n\frac{1}{{\omega }_i}$.Let H₂(λ) = (λ − m − 2)Q_n−1(λ) − Q_n−2(λ) = d_nλⁿ + ⋯ + d₂λ² + d₁λ + d₀, then,

Based on the Vieta theorem,

Second, we calculate ${\sum }_{i=2}^{n+1}\frac{1}{{\psi }_i}$.Let $\frac{J_2(\lambda )}{\lambda }=e_{n+1}{\lambda }^n+e_n{\lambda }^{n-1}\cdots +e_2\lambda +e_1$. We use the Vieta theorem again, ${\sum }_{i=2}^{n+1}\frac{1}{{\psi }_i}=-\frac{e_2}{e_1}$. Because of J₂(λ) = (λ² − (m + 2)λ + m)Q_n−1(λ) − (λ − m)Q_n−2(λ), therefore, e₁ = (−1)ⁿ⁻²(mn + 1), e₂ = (−1)ⁿ⁻¹ + (−1)ⁿ⁻¹(n − 1) (mn + n + 2)/2 + (−1)ⁿ⁻³m(n − 2) (n − 1)n/6. Then,

Therefore, $H^{(1b)}=\frac{1}{2(mn+1)}[\frac{(m-1)[2+(n-1)(mn+n+2)]}{2(m+1)}+\frac{6+3(n-1)(mn+n+2)+m(n-2)(n-1)n}{6(mn+1)}]$.

3.3 The First-Order Coherence of Symmetric Star Topology Networks S^c(m, n)

The symmetric star topology networks with fully connected nodes at the third layer are denoted as S^c(m, n). As is shown in Figure 1C. Let the Laplacian matrix of S^c(m, n) be L³, the characteristic polynomial is P₃(λ) = |λI − L³|. |λI − L³| =

where ⊗ = λ − m − 1.

Similar to Theorem 1, $P_3(\lambda )={[H_3(\lambda )]}^{m-1}{J}_3(\lambda )$, where H₃(λ) = (λ² − (m + 4)λ + 2m + 3)Q_n−2(λ) − (λ − 2)Q_n−3(λ), $J_3(\lambda )=[({\lambda }^3-(m+4){\lambda }^2+(3m+3)\lambda -m)Q_{n-2}(\lambda )-\left(({\lambda }^2-(m+2)\lambda +m)Q_{n-3}(\lambda )\right.]$.

The zero eigenvalue of P₃(λ) appears J₃(λ), let 0 < θ₁ ≤ θ₂ ≤ θ₃ ≤ ⋯ ≤ θ_n be the Laplacian eigenvalues of H₃(λ), 0 = ν₁ ≤ ν₂ ≤ ν₃ ≤ ⋯ ≤ ν_n ≤ ν_n+1 be the Laplacian eigenvalues of J₃(λ).

Theorem 3. The first-order coherence of S^c(m, n) is$H^{(1c)}=\frac{1}{2(mn+1)}[\frac{(m-1)[2(m+3)+(n-2)(2mn+n-2m+3)]}{2(2m+1)}+\frac{6(m+3)+3(n-2)(2mn+n+3)+m(n-3)(n-2)(n-1)}{6(mn+1)}]$.Proof. Similar to Theorem 1,

First, we calculate ${\sum }_{i=1}^n\frac{1}{{\theta }_i}$.Let H₃(λ) = [(λ² − (m + 4)λ + 2m + 3)Q_n−2(λ) − (λ − 2)Q_n−3(λ)] = f_nλⁿ + ⋯ + f₂λ² + f₁λ + f₀, then, f₀ = (−1)ⁿ⁻²(2m + 1), $f_1={(-1)}^{n-1}(m+3)+{(-1)}^{n-3}\frac{(n-2)(2mn+n-2m+3)}{2}$.By the Vieta theorem,

Second, we calculate ${\sum }_{i=2}^{n+1}\frac{1}{{\nu }_i}$. Let $\frac{J_3(\lambda )}{\lambda }=g_{n+1}{\lambda }^n+g_n{\lambda }^{n-1}\cdots +g_2\lambda +g_1,\mathrm{then}g$₁ = (−1)ⁿ⁻²(mn + 1), $g_2={(-1)}^{n-1}(m+3)+{(-1)}^{n-3}\frac{(n-2)(2mn+n+3)}{2}+{(-1)}^{n-3}\frac{m(n-3)(n-2)(n-1)}{6}$.Then,

Therefore, $H^{(1c)}=\frac{1}{2(mn+1)}[\frac{(m-1)[2(m+3)+(n-2)(2mn+n-2m+3)]}{2(2m+1)}+\frac{6(m+3)+3(n-2)(2mn+n+3)+m(n-3)(n-2)(n-1)}{6(mn+1)}]$.

4 Numerical Simulation Experiment and Analysis

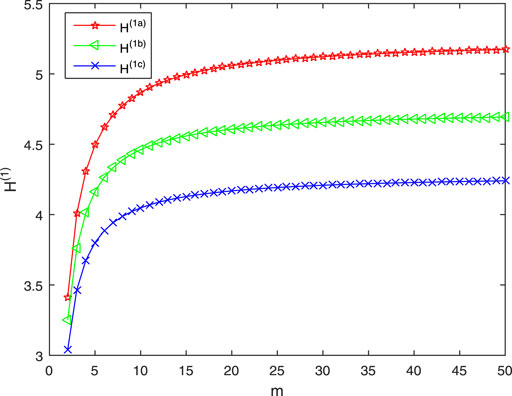
When n = 20, Figure 2 shows the relationships among the first-order coherence H^(1a)(H^(1b), H^(1c)) of S^a(m, n) (S^b(m, n), S^c(m, n)) and m. As m increases to 50, H^(1a) increases from 3.4146 to 5.1731, H^(1b) increases from 3.2520 to 4.6932, H^(1c) increases from 3.0390 to 4.2402. The smaller H⁽¹⁾ is, the better the consensus of the network is. Therefore, when n is fixed, the consensus of three networks get weaker with the increase of m. The consensus of S^a(m, n) is the worst, S^c(m, n) is the best. Further, when m is sufficiently large, the first-order coherence of three networks are close to the fixed value, and the consensus of three networks will not weaken with the increase of m.

FIGURE 2. Comparison of three networks H⁽¹⁾ with m.

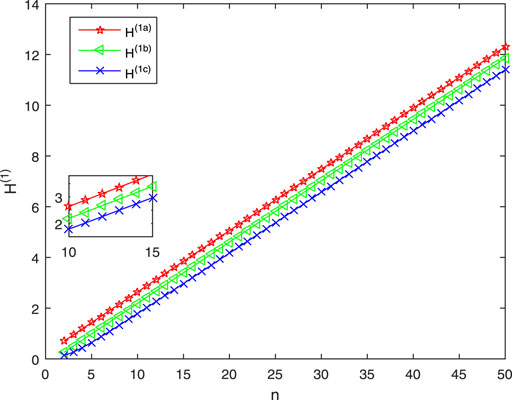
When m = 20, Figure 3 shows the relationships among the first-order coherence H^(1a)(H^(1b), H^(1c)) and n. As n increases to 50, H^(1a) monotonically increased from 0.702 to 12.3089, H^(1b) monotonically increases from 0.2606 to 11.8569, H^(1c) monotonically increases from 0.1368 to 11.3969. Therefore, when m is fixed, the consensus of three networks get weaker with the increase of m, and the consensus of S^a(m, n) is the worst, S^c(m, n) is the best.

FIGURE 3. Comparison of three networks H⁽¹⁾ with n.

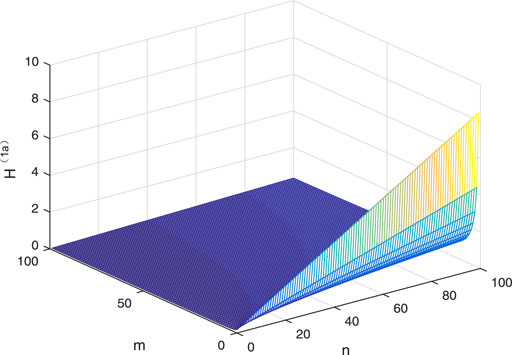
Figure 4 shows the relationships among the first-order coherence H^(1a) of S^a(m, n) and the parameters m and n as a special case. When m and n increase to 100, the consensus of network continues to weaken. We find that the effect of n on consensus is much stronger than m.

FIGURE 4. The relationship among H^(1a) and m, n.

5 Main Results

This paper studies the consensus of three kinds of symmetric star topology networks. Based on the relationships between Laplacian eigenvalues and characteristic polynomial coefficients, the specific expressions of three kinds of network coherence are calculated. Numerical simulation experiments verify the validity of the theoretical results. When the length of the path n in the symmetric star topology networks are fixed, with the increase of the number of branches m, the consensus of three kinds of networks first weaken and then remain unchanged, the consensus of S^a(m, n) is the worst, S^c(m, n) is the best. When the number of branches m in the networks are fixed, the consensus of the three kinds of networks become weaker with the increase of the length of the path n, the consensus of S^a(m, n) is the worst, S^c(m, n) is the best. When m and n change at the same time, the effect of n on consensus is much stronger than m.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization, HG and JZ; methodology, HG and JZ; software, LZ and XC; validation, HG, JZ, and XL; formal analysis, HG and XC; writing—original draft preparation, HG and JZ; writing—review and editing, XL; supervision, XL and XC; project administration, HG. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (no. 61802316) and the National Science Foundation of Xinjiang (NSFXJ) (no. 2021D01A65), the National Science Foundation of Xinjiang (NSFXJ) (no. 2021D01B35), Scientific Research Project of Xinjiang Institute of Engineering (no. 2012XGZ111312), School level project of Xinjiang institute of Light industry Technology (no. XJQG2022S16), National innovation and entrepreneurship training program for College Students (no. 202110994006).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We express our sincere gratitude to the persons who gave us valuable comments.

References