Topological States in Two-Dimensional Su-Schrieffer-Heeger Models

1 Introduction

Topological phases of matter have attracted tremendous research interests in recent decades [1, 2]. Among those famous topological models, the 1D Su-Schrieffer-Hegger (SSH) model provides a prototype and simple model endowed with rich physics to investigate topological phenomena in condensed matter physics [3]. It exhibits fascinating topological properties such as the topological phase transitions associated with Zak phase and fractional fermions number at the ends of the sample [3]. It also helps to clarify the theory of bulk polarization based on Berry phase [4], which has wide and deep impacts on condensed matter physics in recent decades, especially on the development of topological band insulators [5, 6].

Recently, the 1D SSH model has been extended to 2D on a square lattice. For instance, Liu et al. found that the 2D SSH model shows nontrivial topological phases even the Berry curvature is zero in the whole BZ [7]. Benalcazar et al. extended the 1D SSH model to two-, and three-dimensional systems with a π-flux inserted at each plaquette of the lattice. The proposed Benalcazar-Bernevig-Hughes (BBH) models hold quantized bulk quadrupole and octupole moments in 2D and 3D, respectively [8, 9]. Similar to 1D SSH model, bound states carrying fractional charges exist at the corners of the system. Thus the BBH provides a concert example for the higher-order topological insulators (HOTIs). Such HOTIs generalize the conventional bulk-boundary correspondence. Typically, a topological bulk state in d-dimension has robust (d − 1)-dimensional boundary states. Nevertheless, HOTIs have localized states at boundaries that are two or three dimensions lower than the bulk. The HOTIs have consequently attracted both theoretical and experimental interest over past years [10–31], and the higher-order topological protection has been extended to superconductors [32–38] and semimetals [39–41].

Since several types of 2D SSH models are possible when generalizing the 1D SSH model, it is thus natural to ask whether these models exhibit interesting topological properties. In this work, we investigate the properties of two typical kinds of 2D SSH models. Remarkably, we find that these models have rich topological phases. In the semimetallic phase, a pair of Dirac points appear in the BZ. Interestingly, the locations of the Dirac points are not pinned but can be easily tuned by continuous parameter modulations without breaking any symmetries. The merging of two Dirac points will experience a novel topological phase transition which transform the system to either a weak topological insulator or a nodal-line metallic phase. We demonstrate the topological properties of these different phases by employing two independent winding numbers together with boundary signatures and symmetry arguments. We also discuss how to realize our model experimentally based on synthetic quantum materials.

The remainder of this paper is organized as follows. Section 2 introduces the type-I 2D SSH model and its band structure. Section 3 presents the semimetallic phases of the type-I 2D SSH model. Section 4 shows the anisotropic nature of type-I 2D SSH model. Section 5 considers properties of type-II 2D SSH model. Finally, we conclude our results with a discussion in Section 6.

2 Type-I Two-Dimensional Su-Schrieffer-Heeger Model

Let us focus on the type-I 2D SSH model first [42]. We consider a type-I 2D SSH model as shown in Figure 1A, where the weak (thin) bonds and strong (thick) bonds are alternately dimerized along the two adjacent parallel lattice rows (x-direction) or columns (y-direction). The four orbital degrees of freedom in each unit cell are labeled as 1–4. For clarity, we consider spinless fermions. The lattice Hamiltonian is

where $C_{\mathbf{R},i}^{†}$ is the creation operator for the degree of freedom i in the unit cell R with i = 1, 2, 3, 4, as shown in Figure 1A. Transforming it into the reciprocal space, the effective Bloch Hamiltonian describing the type-I 2D SSH model reads

where k = (k_x, k_y) is the 2D wave-vector; t and t_x/y are the staggered hopping amplitudes along x/y-directions. For simplicity, we put the lattice constant to be unity and assume t > 0 hereafter. From its off-diagonal form, the Hamiltonian in Eq. 2 respects chiral (sublattice) symmetry. Explicitly, the chiral symmetry is $\mathcal{C}H(\mathbf{k}){\mathcal{C}}^{-1}=-H(\mathbf{k})$ with the chiral-symmetry operator $\mathcal{C}={\tau }_3\otimes {\sigma }_0$, where τ and σ are Pauli matrices for different orbital degrees of freedom in the unit cell. The energy bands and corresponding wave functions can be obtained analytically. The energy bands of Eq. 2 are

where we have defined ${\xi }_{\eta }(\mathbf{k})\equiv (t+t_x)\cos \frac{k_x}{2}+\eta (t+t_y)\cos \frac{k_y}{2}$, ${\zeta }_{\eta }(\mathbf{k})\equiv (t-t_x)\sin \frac{k_x}{2}-\eta (t-t_y)\sin \frac{k_y}{2}$, and ɛ_η(k) ≡ ξ_η(k) + iζ_η(k) with η = ±1. The convenient form of energy bands Eq. 4 will help us to locate the Dirac points and identify the phase diagram of the system.

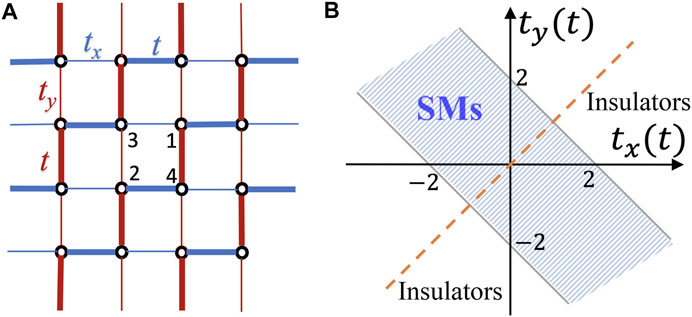
FIGURE 1. (A) Schematic of the type-I 2D SSH lattice. Blue (red) thick and thin bonds mark alternately dimerized hopping amplitudes in x(y)-direction. (B) The full phase diagram of the type-I 2D SSH model in the parameter space (t_x, t_y). The shadowed region represents the semimetals (SMs) with a pair of Dirac points. The orange dashed line at t_x = t_y corresponds to a nodal-line metallic phase. Other regions are the weak topological insulators.

3 Semimetallic Phases

The type-I 2D SSH model actually possesses three different topological phases, as shown in the phase diagram Figure 1B. Here we first discuss the semimetallic phase with a pair of Dirac points within the region |t_x + t_y| < 2t and t_x ≠ t_y. Due to the presence of chiral symmetry, the conduction and valence bands touch at zero energy (Figure 2A). Thus, the existence of Dirac points is constrained by the conditions ξ_η(k) = ζ_η(k) = 0. Consequently, we find a pair of Dirac points located at K_± ≡±(K_x, − K_y), where K_x/y are given by

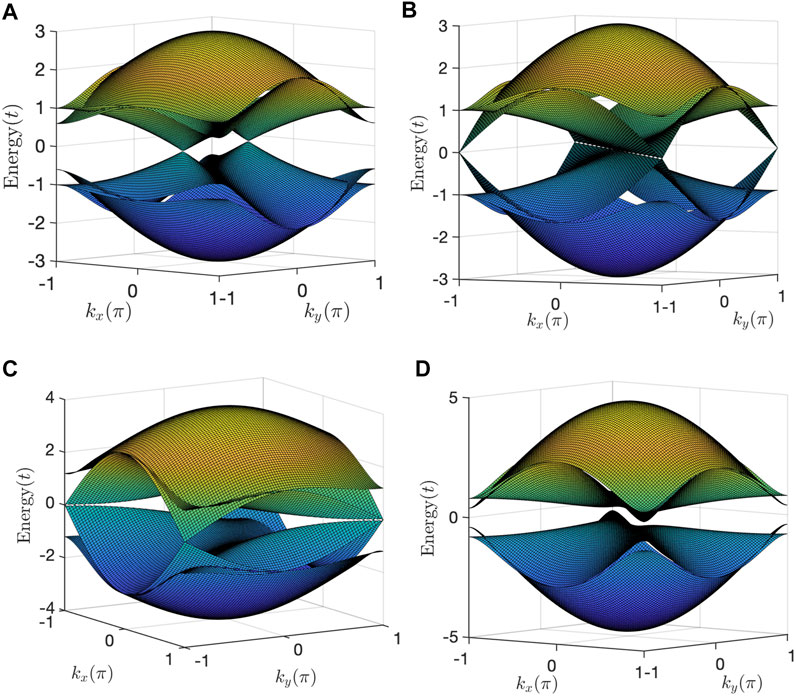
FIGURE 2. Band structure in different phases of type-I 2D SSH model. (A) Band structure in the semimetallic phase with t_x = 0.2t and t_y = 0.8t. (B) Band structure for the nodal-line metallic phase with t_x = t_y = 0.5t. (C) Band structure for a critical phase point with t_x = 1.6t and t_y = 0.4t. (D) Band structure for the weak topological insulators with t_x = 1.6t and t_y = 1.2t.

Astonishingly, the Dirac points are not pinned to any high-symmetry points but are highly tunable by parameter modulations. If we consider a simple parameterization with t_x = s ∈ [0, t], t_y = t − s, and t = 1, we find that the relation K_x + K_y = 2π/3 holds true. As a result, the Dirac points move along a line segment when we vary the parameter s. Interestingly, no symmetries are broken as we move around Dirac points by variation of t_x and t_y. The Dirac points are topologically protected by a quantized charge $Q_{{\mathbf{K}}_{\pm }}={\frac{1}{2\pi i}\oint }_{\ell }d\mathbf{k}\cdot \mathrm{Tr}\left[q^{-1}(\mathbf{k}){\nabla }_{\mathbf{k}}q(\mathbf{k})\right]$, where the loop ℓ is chosen such that it encircles a single Dirac point K_± [43, 44]. In essence, it is based on the π Berry phase, which is actually the same as in graphene. The two Dirac points in the BZ have opposite topological charges $Q_{{\mathbf{K}}_{\pm }}=\pm 1$. They annihilate each other when they meet in k-space.

Let us then turn to the nodal-line metallic phase under the specific condition t_x = t_y [Figure 2B]. From Eq. 4, we find that the system exhibits a gapless nodal line at

The appearance of a gapless nodal line is a direct consequence of accidental mirror symmetry along the line x + y = 0. In momentum space, the mirror symmetry is expressed as MH(k_x, k_y)M⁻¹ = H( −k_y, − k_x). Note that the Hamiltonian H(k) commutes with the mirror operator M along the nodal-line k_x + k_y = 0. Therefore, we can label the eigen states of the Hamiltonian H(k) by the eigen states of mirror operator M as

We further note that the mirror operator commute with the chiral symmetry operator, i.e., $[\mathcal{C},M]=0$. Therefore, we can show that $\mathcal{C}|+\rangle$ is also an eigenstate of M with eigen value +1. Moreover, $\mathcal{C}|+\rangle$ is eigenstate of H(k) with energy + E. Actually, the chiral symmetry maps the state | + ⟩ with energy + E to state $\mathcal{C}|+\rangle$ with energy − E. This implies that those states are degenerated states at energy E = 0.

4 Weak Topological Insulating Phases

The merging of two Dirac points can transfer the system from the semimetallic phase to a weak topological insulator, which provides a novel type of topological phase transition. Figure 2C presents the band structure at the critical merging points, at which the spectrum stays linear along one direction while becomes parabolic along another direction [45]. Specifically, the weak topological insulators is located in the region |t_x + t_y| > 2t and t_x ≠ t_y. The weak topological insulators possess a direct band gap, see Figure 2D. It is described by two winding numbers (w_x, w_y) with one of them being one and the other being zero. The winding number is defined as

for arbitrary k_y/x ∈ [0, 2π]. Actually, this weak topological insulators can be further divided into two subphases: (i) w_x = 1, w_y = 0 (t_x > t_y and |t_x + t_y| > 2t) and (ii) w_x = 0, w_y = 1 (t_x < t_y and |t_x + t_y| > 2t). When w_x = 1, w_y = 0 (w_x = 0, w_y = 1), the system is nontrivial along x(y)-direction and trivial along y(x)-direction. It is clear that once crossing the boundary t_x = t_y the system will shift from subphase (i) to subphase (ii) or vice versa. Correspondingly, a totally flat edge band exists in the gap of the energy spectrum of a ribbon along x(y)-direction for the subphase (i) [subphase (ii)]. Figures 3A,B present the band structure of a ribbons along x- and y -direction, respectively, for the subphase (ii). The flat edge bands exist only in Figure 3A. Notably, neither the topologically trivial insulator with w_x = w_y = 0 nor the nontrivial phase with w_x = w_y = 1 appear in the inclined 2D SSH model.

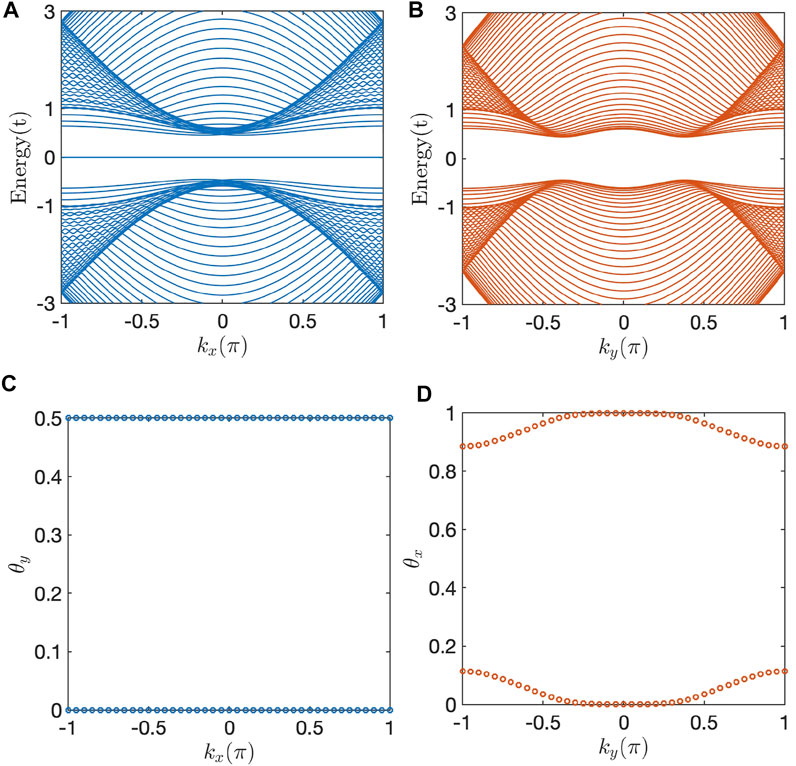
FIGURE 3. (A) Energy spectrum of a ribbon along x-direction with width W_y = 20. Notice the flat band at zero energy. (B) Energy spectrum of the ribbons along y-direction with width W_x = 20. (C) Wannier bands θ_y as a function of k_x. (D) Wannier bands θ_x as a function of k_y. The other parameters are t_x = 1.2t and t_y = 1.8t.

Furthermore, the calculation of Wannier bands can also provide consistent results with that of w_x/y to identify the topological properties. Specifically, the Wilson loop operator parallel to y direction is constructed as [9, 46].

where each projection operator is defined as $P_{m\delta k_y+k_y}\equiv {\sum }_{n\in N_{\text{occ}}}|u_{k_x,m\delta k_y+k_y}^n\rangle \langle u_{k_x,m\delta k_y+k_y}^n|$ with $|u_{k_x,m\delta k_y+k_y}^n\rangle$ being the n-th eigen state of occupied bands at point (k_x, mδk_y + k_y), and m is an integer taking values from {1, 2, …, N_y}. The projection method can avoid the arbitrary phase problem in numerical realizations. Here N_y is the number of unit cells, n is the band index, and N_occ is the number of occupied bands. Note that ${\widehat{P}}_{y,\mathbf{k}}$ has dimension of N now with N being the total bands number. After projection onto the occupied bands at base point k, there is N_occ × N_occ matrix ${\mathcal{W}}_{y,\mathbf{k}}$ that defines a Wannier Hamiltonian $H_{{\mathcal{W}}_y}(\mathbf{k})$ from the relation ${\mathcal{W}}_{y,\mathbf{k}}=\exp [i{H}_{{\mathcal{W}}_y}(\mathbf{k})]$. The eigen values of $H_{{\mathcal{W}}_y}(\mathbf{k})$ give the Wannier bands 2πθ_y(k_x) associated with eigen states $|{\theta }_{y,\mathbf{k}}^j\rangle$, j ∈ {1, 2, …, N_occ}. The Wannier bands plotted in Figures 3C,D are corresponding to the cases in Figures 3A,B. It is clear the two occupied bands in Figure 3C gives a quantized half-integer polarization while the two occupied bands in Figure 3D gives a zero polarization (mod 1). The quantized half-integer polarization indicates the nontrivial topological properties.

5 Type-II Two-Dimensional Su-Schrieffer-Heeger Model

Now, let us consider another similar model: the type-II 2D SSH model, in which the alternatively dimerization pattern is shown in Figure 4A. The lattice Hamiltonian reads as

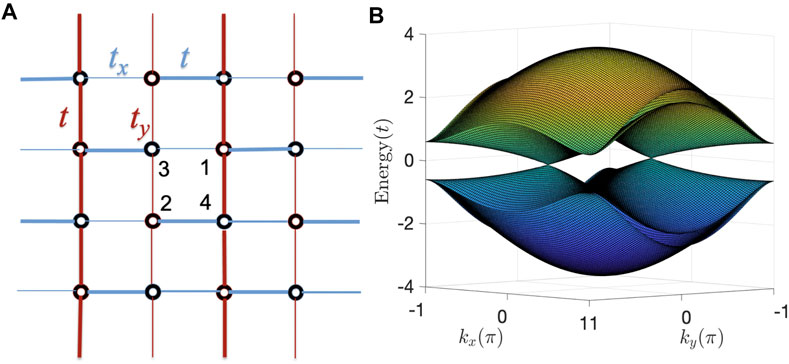
FIGURE 4. (A) Schematic of the type-II 2D SSH lattice. Blue (red) thick and thin bonds mark alternately dimerized hopping amplitudes in x(y)-direction. (B) The band structure with at pair of Dirac points. Her we take t_x = 0.4t, t_y = 1.2t.

The type-II model has many similarities with the type-I model, thus we just focus on the semimetallic phase with Dirac points here. The effective Bloch Hamiltonian describing the type-II 2D SSH model has the same form as Eq. 2 but with the off-diagonal parts replaced as

Its energy bands are

where we have defined the functions as $h_0(\mathbf{k})\equiv {(t-t_x)}^2+4t_{x}t{\cos }^2\frac{k_x}{2}+2(t^2+t_y^2){\cos }^2\frac{k_y}{2}$, $h_x(\mathbf{k})\equiv 2\cos \frac{k_y}{2}\left[t(t_x+t_y)\cos (k_x+k_y/2)+(t^2+t_x{t}_y)\cos \frac{k_y}{2}\right]$, $h_y(\mathbf{k})\equiv 2\cos \frac{k_y}{2}\left[t(t_x+t_y)\sin (k_x+\frac{k_y}{2})+(t^2+t_x{t}_y)\sin \frac{k_y}{2}\right]$, and $h_z(\mathbf{k})\equiv 2(t^2-t_y^2){\cos }^2\frac{k_y}{2}$. The type-II model has a glide-mirror symmetry: performing a mirror symmetry M_x and then a half translation g_y along y-direction, the system goes back to itself.

Its Dirac points are located along k_x = 0 (or k_x = π) when t_y > 0 (or t_y < 0) (see Figure 4D). Explicitly, the Dirac points locate at $(0,\pm 2\arccos \sqrt{\frac{{(t+t_x)}^2}{4t{t}_y}})$ for t_y > 0 or $(\pi ,\pm 2\arccos \sqrt{\frac{{(t-t_x)}^2}{-4t{t}_y}})$ for t_y < 0. Corresponding, the physical solutions hold under the condition ${(t+t_x)}^2<4t_{y}t$ or ${(t-t_x)}^2<-4t_{y}t$. The effective Hamiltonian close to the Dirac points can also be obtained analytically. For simplicity, let us focus on the case of t_y > 0. To this end, we need to get the two zero-energy eigen states at the Dirac points as a basis and then project the full Hamiltonian to the basis. Finally, the effective Hamiltonian is expressed as

where $v_x=\frac{\sqrt{t_{y}t}(t-t_x)}{t+t_y}$, and $v_y=\mathrm{sgn}(t+t_x)\frac{\sqrt{t_{y}t(4t_{y}t-{(t+t_x)}^2)}}{t+t_y}$.

6 Discussion and Conclusion

Here we discuss how to realize our proposals experimentally. The most important ingredient is the controllable nearest-neighbor couplings between sites on the square lattice. Fortunately, such techniques have been developed in synthetic quantum materials such as photonic and acoustic crystals [14, 28, 47–49], electric circuits [50], and waveguides [15, 51]. For instance, to realize our model in an acoustic system, the 3D printed “atoms” can be arranged to a square lattice with four contained in each unit cell and the alternately dimerized couplings between neighbors can be modulated the diameters that the sound wave go through. Another feasible platform to realize our model is based on ultracold gases in optical lattices [52, 53], in which the lattice geometry and hopping strengths are adjustable.

Note that our results are distinctively different from recent reports to realize Dirac states in square lattices [54–56]. These proposals require necessary π fluxes on each plaquette, and the Dirac points are pinned to boundaries of the BZ, which may makes it more difficult to detect experimentally. While our 2D SSH model does not require delicate manipulations of external flux. Interestingly, our models even provide platforms to realize the so called toric-code insulator [56].

In conclusion, we have proposed the 2D SSH models on a square lattice to realize tunable Dirac states. We have found that the locations of Dirac points are not pinned in the BZ but movable by parameter modifications. The merging of two Dirac points leads to a topological phase transition, which converts the system from a semimetallic phase to either a nodal-line metallic or a weak topological insulator. We expect that our model can be realized in different metamaterial platforms.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

C-AL initiated the project, derived the results and wrote the manuscript.

Funding

This work was supported by the DFG (SPP1666 and SFB1170 “ToCoTronics”), the Würzburg-Dresden Cluster of Excellence ct.qmat, EXC2147, Project-id 390858490, and the Elitenetzwerk Bayern Graduate School on “Topological Insulators”, and the NSF of Zhejiang under Grant No. Q20A04005.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The author acknowledges S. B. Zhang, S. J. Choi, B. Fu, and B. Trauzettel for helpful discussions.

References