Bioconvection Maxwell nanofluid flow over a stretching cylinder influenced by chemically reactive activation energy surrounded by a permeable medium

Khan, Arshad; Iqbal, Zahoor; Ahammad, N. Ameer; Sidi, Maawiya Ould; Elattar, Samia; Awad, Somia; Yousef, El Sayed; Eldin, Sayed M

doi:10.3389/fphy.2022.1065264

ORIGINAL RESEARCH article

Front. Phys., 12 January 2023
Sec. Mathematical Physics
Volume 10 - 2022 | https://doi.org/10.3389/fphy.2022.1065264

Bioconvection Maxwell nanofluid flow over a stretching cylinder influenced by chemically reactive activation energy surrounded by a permeable medium

Arshad Khan¹*

Zahoor Iqbal^2,3 www.frontiersin.org

N. Ameer Ahammad⁴ www.frontiersin.org

Maawiya Ould Sidi⁵ www.frontiersin.org

Samia Elattar⁶ www.frontiersin.org

Somia Awad⁷ www.frontiersin.org

El Sayed Yousef^8,9

Sayed M Eldin¹⁰

¹College of Aeronautical Engineering, National University of Sciences and Technology (NUST), Islamabad, Pakistan
²Department of Mathematics, Quaid-i-Azam University, Islamabad, Pakistan
³Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
⁴Department of Mathematics, Faculty of Science, University of Tabuk, Tabuk, Saudi Arabia
⁵RT-M2A Laboratory, Mathematics Department, College of Science, Jouf University, Sakaka, Saudi Arabia
⁶Department of Industrial and Systems Engineering, College of Engineering, Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia
⁷Physics Department, Al-Qunfudah University College, Umm Al-Qura university, Mecca, Saudi Arabia
⁸Physics Dep, Faculty of Science, King Khalid University, Abha, Saudi Arabia
⁹Research Center for Advanced Materials Science (RCAMS), King Khalid University, Abha, Saudi Arabia
¹⁰Center of Research, Faculty of Engineering, Future University in Egypt, New Cairo, Egypt

The role of nanofluids in the development of many electronic devices at the industrial level is very significant. This investigation describes the thermal exploration for a bioconvective flow of Maxwell nanoparticles over stretching and revolving the cylinder placed in a porous medium. The fluid flow is in contact with chemically reactive activation energy. The swirling flow is induced by the stretching rotary cylinder. The magnetic effect of constant strength $B_{0}$ is practiced to the flow system in combination with thermally radiative effects and a heat source/sink for controlling the thermal effects upon the flow system. The thermophoretic and Brownian motion characteristics, due to the nanofluid flow, are captured by implementing the Buongiorno model. The central focus of this study is to explore the thermal and mass transfer for the flow problem accompanied by motile microorganisms. The governing equations have been converted to the dimensionless form with similar variables, and the homotopy analysis method (HAM) has then been applied for solution. It has been concluded in this investigation that fluid flow decays for escalation in the Maxwell, porosity, and magnetic parameters, and Forchheimer and bioconvection Rayleigh numbers, while upsurges with the augmenting values of the Buoyancy factor. With the increasing values of the Brownian number, thermophoretic and radiation factors upsurge the thermal profiles and decline the concentration profiles. Moreover, the density of motile microorganisms declines with the expansion in the Peclet number. The range for $η$ is taken from 0 to seven to get the convergence of the graph.

Introduction

Bioconvection is the scattering of gyrotactic microorganisms through a contracted deferment. It is the convective fluid flow at the microscopic level due to the variations in density, which is produced by the collective spinning of motile microorganisms. The spinning characteristics of gyrotactic microorganisms are of dynamic significance to comprehend a number of biological characteristics associated with bioconvection. This awareness of bioconvection was first introduced by Platt [1] for investigating its pattern through free swimming in a dense culture. Ahmad et al. [2] inspected the bioconvective Maxwell nanofluid flow with thermally radiative effects. Sajid et al [3] studied the influence of microorganisms along with variable diffusivity of species for blood-gold Reiner–Philippoff nanoparticles. Waqas et al. [4] numerically simulated the bioconvective nanofluid flow with the influence of motile microorganisms and have numerically revealed the impact of different factors upon flow profiles. Shahzad et al. [5] explored the electro magnetohydrodynamics (EMHD) nanoliquid flow past an extending sheet with the influence of microorganisms and have concluded that thermal flow has augmented with the growth in the thermal Biot number. Safdar et al. [6] discussed the EMHD nanofluid flow past an extending sheet subjected to microorganisms and effects of Arrhenius activation energy and have claimed that thermal profiles have augmented with growth in the values of the mixed convective factor. Abdelmalek et al. [7] mathematically established a model for the bioconvective flow of nanoliquids past a revolving cylinder. The slip effects along with thermal conductivity have been used to the flow system by the authors of this study and then have been used to determine the approximate solution of the resultant equations. Hamid et al. [8] numerically studied the bioconvective magnetohydrodynamics (MHD) nanofluid flow with the influence of microorganisms and have revealed that thermal distribution has augmented with an upsurge in the Biot number and radiation factor. Rana et al. [9] scrutinized the swimming process of microbes in blood flow with the nano-bioconvection Williamson fluid model. In this study, the finite difference method has been used by the authors to carry out the stability and convergence analysis.

The transfer of mass in different species normally takes place for variations related to such species. The migration of species in such a phenomenon from a region of higher to lower concentration has been observed. Examples include handling of foods, diffusion of nutrients, and thermal insulation. In the past few decades, mass transfer using chemical reactions has persisted in an interested area for various researchers. Chamkha et al. [10] studied the mass and thermal flows for varying thermal and mass diffusions with the influence of chemical reactions and have revealed that fluid motion has declined with growth in the chemical factor, due to which less mass has diffused. Mabood et al. [11] explored the micropolar fluid flow upon a thin moving needle subjected to Soret and Dufour effects and have established that the micropolar factor has upsurged the rotary motion. Sarada et al. [12] studied the influence of exponentially growing inner heat generation over the trihybrid nanoliquid flow over an extending curved sheet. The lowest essential energy for starting a reaction chemically is called the activation energy. This term was first familiarized by Arrhenius [13]. The activation energy is the magnitude of energy that is mandatory for a reactant to convert into a product. It is understood that all molecules have some energy either in the form of potential energy or kinetic energy. This energy can be used to first stretch, then to turn, and finally to disrupt the bonds among the molecules that lead to a chemical reaction. The idea of activation energy is closely related to oil emulsion and oil repository engineering. In recent times, the collective impact of chemically reactive activation energy has gained more importance due to its applications in industries. Many investigations have been carried out with the main focus upon the concept of mass transfer in a flow system. Maleque [14] investigated the impact of activation energy upon the MHD flow past a penetrable medium. Jayaparkash et al. [15] studied the activation energy and heat convection for the radiative hybrid nanofluid flow over a curved surface. Sajid et al. [16] elaborated the influences of chemically reactive energy of the trihybrid nanoparticle flow over the wedge and have concluded that the heat flow behavior of the fluid has amplified for three nanoparticle suspensions in pure fluids.

The mixing of nano-sized particles in the base fluid is termed as the nanofluid. It has revealed that the heat conduction characteristics of the pure fluid augment by combining the nanoparticles to pure fluids. Since the nanofluid has augmented heat convection characteristics, these fluids have numerous engineering and industrial applications, like solar collectors and radiators, and hybrid power engines. Different established works can be found with the main focus upon the heat transfer characteristics by applying different flow conditions and geometries. Choi [17] stood as the first nobleman to propose the use of nanoparticles in pure fluids. Sajid et al. [18–20] deliberated upon fluid flow and heat transfer using different physical flow geometries and various flow conditions subjected to suspension of nanoparticles in pure fluids. Saleem et al. [21] deliberated the water-based nanofluid flow past a horizontal sheet using three different shapes of nanoparticles. Cao et al. [22] simulated the dynamical colloidal combination of nanoparticles and water using different levels of slips of partial nature. Animasaun et al. [23] deliberated on trihybrid nanoparticle flow over a heated surface and have concluded that heat flow has been augmented with the growth in volume fraction. Xiu et al. [24] examined the nanofluid flow for a dual-stretched wage surface using forced convective effects subjected to variations in temperature.

The flow of fluids upon stretching cylinders has appealed the intuition of various scientists and researchers. Its different applications include crystal production, paper manufacturing, fabrication of glass, and polymer extrusion. Due to such important applications of flow over stretching cylinders, many investigations have been carried out for these flows with the main emphasis upon thermal and mass transfer. Kumar et al. [25] studied the MHD hybrid nanofluid flow past a stretching cylinder and have concluded that fluid motion has declined with the upsurge in the ferromagnetic factor. Naveen Kumar et al. [26] conducted a detailed study on the ferromagnetic fluid flow upon a stretching cylinder. Varun Kumar et al. [27] used the modified Fourier thermal flux for investigating the double-phase flow of the dusty fluid with the hybrid nanofluid past an extending cylinder and have revealed that an upsurge in mass concentration has declined the fluid motion and thermal gradient. Benaziza et al. [28] studied the production of irreversibility amid two coaxial cylinders using an improved ADM for the solution of modeled equations. Eid et al. [29] used blood-based single-walled carbon nanotube (SWCNT) nanofluid past a cylinder immersed by a permeable medium with the effects of EMHD radiations and have concluded that due to the SWCNT flow, thermal distributions have been augmented. Jamshed et al. [30] explored the MHD-mixed convection nanoparticle flow through a vented cavity with an inner elliptic cylinder. Punith et al. [31] scrutinized the Darcy–Forchheimer dusty hybrid nanofluid flow past a cylinder and have concluded that the growth in the fluid motion interaction factor has declined the gradient in velocity for the fluid phase and upsurge velocity for the dust phase. Khan et al. [32] observed the output of convective heat transmission upon the nanofluid flow over a stretching cylinder. It has been highlighted in this study that the Deborah number has augmented the flow and has declined the heat transfer rate.

A medium that contains pores or void spaces in it is termed as a porous medium, and its examples include rubber, wood, and some rocks. A number of porous media are available naturally, but they can also be fabricated. There are abundant applications of porous medium at the industrial level such as filtration and purification processes, seepage of water in sand beds, and drying of porous material in the textile industry. These attractive uses have fascinated the attention of various researchers and scientists. In light of the Darcy Law, the flow of fluid depends linearly upon the pressure gradient and gravitational force. Whenever the porous medium is packed closely, then this law supports the equation of motion for Newtonian fluids with small values of Reynolds number. But for larger pores in the medium, there will be large void spaces in it that leads to viscous shear in addition to Darcy confrontation. In light of this study, P. Forchheimer [33] comprehended the concept of Darcy and has included the square of the flow term in the flow equation for evaluating the inertial forces. Later, Muskat [34] named this term as the Forchhiemer term. Subsequently, many studies have been conducted through porous media by various investigators by focusing on the transmission of heat and mass with different flow conditions. Pandey and Kumar [35] discussed the influence of heat radiation with natural convection upon nanofluids flowing on the stretched cylinder and porous surface. Benos et al. [36] explored the natural convective MHD fluid flow over a saturated permeable enclosure. Redouane et al. [37] inspected the influences of irreversibility upon MHD hybrid nanoparticles through a rotary cylinder subjected to the Brinkman–Forchheimer model and have concluded that augmentation in Darcy and Rayleigh numbers has caused an upsurge in the values of thermal flow convection in the surrounding area of enclosure.

In the Universe, most of the physical problems when modeled mathematically are transformed to the non-linear form. The determination of the exact solution for such problems is very difficult, rather sometimes it is impossible to solve these non-linear problems. So these problems can be solved by employing either a numerical or semi-numerical technique. In the current investigation, a semi-numerical technique homotopy analysis method (HAM) [38, 39] has been used to determine the solution to modeled problems in a dimensionless form.

Novelty/originality

From the aforementioned works, it was perceived that many examinations have been conducted with the main focus upon heat and mass transfer over a stretching cylinder, but very few examinations have been conducted with the bioconvection MHD fluid flowing upon a stretching cylinder. However, no work has yet been established for Maxwell nanofluid over a stretching and revolving cylinder that is inserted in a permeable medium with the bioconvective phenomenon, which is the main novelty of the current study. The novelty of this work has improved further by exposing the flow system to the coupled effects of chemically reactive Arrhenius activation energy. Moreover, the magnetic effect with $B_{0}$ as strength is practiced to the flow system. Additionally, the thermophoretic and Brownian motion characteristics due to the nanofluid flow are captured by implementing the Buongiorno model. The main focus of this work is to discover and to improve the heat and mass transfer for a flow system accompanied by gyrotactic microorganisms.

The first section of the manuscript includes the literature review and the novelty of the current work. The second section includes the description of the investigation both physically and mathematically. All parameters encountered in this investigation have been defined in this section. The third section comprises the solution technique and its algorithm. The fourth section includes the discussion about different results. A comprehensive detail of the impact of substantial parameters upon different flow profiles has been discussed in this section. In the last section, the main finding has been concluded to give a broader view to the readers.

Physical and mathematical description

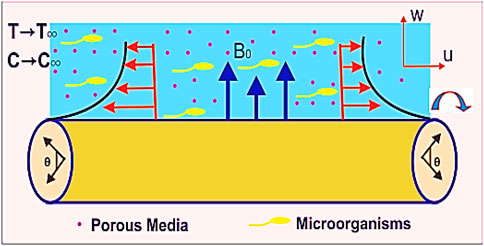
Take the bioconvective swirling motion of the Maxwell nanofluid past a stretching cylinder that is inserted in a permeable medium. The following assumptions have been used in this study:

1) The radius of cylinder is assumed to be $R_{1}$ that is also performing rotary motion.

2) The magnetic effect with $B_{0}$ as the strength is employed to the flow system.

3) To control the thermal effects upon flow, the influence of the heat source, sink, and thermal radiations has been considered.

4) The thermophoretic and Brownian motion characteristics due to the nanofluid flow are captured by implementing the Buongiorno model to the flow system.

5) The $z - a x i s$ is considered along the axis of the cylinder, while the $r - a x i s$ is considered along the radial track.

6) The components of velocity in the directions of $z, θ$ and $r -$ axes are $u, v$ and $w$ , respectively.

7) A collective influence of chemically reactive activation energy has also been experienced by the flow system.

8) The microorganism, concentration, and temperature at the cylinder’s surface are assumed as $n_{w}, C_{w}, a n d T_{w}$ , whereas the corresponding values for free stream are $n_{\infty}, C_{\infty}, {a n d T}_{\infty}$ (see Figure 1).

FIGURE 1

FIGURE 1. Geometry for the flow problem.

Taking into account the aforementioned assumptions, the resultant equations take the following vector form [40–44]:

\begin{array}{c} \begin{array}{c} \nabla . V = 0, \\ ρ \frac{d V}{d t} = - \nabla p + \nabla . S - (σ {B_{0}}^{2} + \frac{υ}{k^{*}}) \frac{u}{ρ} - \frac{1}{ρ \sqrt{k^{*}}} F u^{2} \end{array} \\ \begin{array}{c} + g [\frac{1}{ρ_{f}} {(T - T_{\infty}) (1 - C_{\infty}) β ρ_{f} - (C - C_{\infty}) (ρ_{p} - ρ_{f}) - γ (n - n_{\infty}) (ρ_{m} - ρ_{f})}], \\ \frac{d T}{d t} = τ (D_{B} \nabla C . \nabla T + \frac{D_{T}}{T_{\infty}} {(\nabla T)}^{2}) - \frac{1}{ρ c_{p}} \nabla . q + \frac{Q_{0} (T - T_{\infty})}{ρ c_{p}}, \end{array} \\ \begin{array}{c} \frac{d C}{d t} - \frac{D_{T}}{T_{\infty}} {(\nabla T)}^{2} = - {k_{r}}^{2} (C - C_{\infty}) {(\frac{T}{T_{\infty}})}^{n} \exp (- \frac{E_{a}}{k_{B} T}), \\ \frac{d n}{d t} + \frac{b W_{c}}{(C_{w} - C_{\infty})} [\nabla (n . \nabla C)] = D_{m} \nabla^{2} n . \end{array} \end{array} (a)

In component notation, we have from the aforementioned equation the following continuity equation,

\frac{\partial w}{\partial r} + \frac{w}{r} + \frac{\partial u}{\partial z} = 0, (1)

momentum equation,

\begin{array}{l} w \frac{\partial u}{\partial r} + u \frac{\partial u}{\partial z} + λ_{1} [u^{2} \frac{\partial^{2} u}{\partial z^{2}} + w^{2} \frac{\partial^{2} u}{\partial r^{2}} + 2 w u \frac{\partial^{2} u}{\partial r \partial w}] = υ [\frac{\partial^{2} u}{\partial r^{2}} + \frac{1}{r} \frac{\partial u}{\partial r}] - \frac{υ}{k^{*}} u - \frac{1}{ρ \sqrt{k^{*}}} F u^{2} \\ - \frac{σ {B_{0}}^{2} u}{ρ} + g [\frac{1}{ρ_{f}} \{(T - T_{\infty}) β ρ_{f} - (ρ_{p} - ρ_{f}) (C - C_{\infty}) - γ (n - n_{\infty}) (ρ_{m} - ρ_{f})\}], \end{array} (2)

energy equation,

u \frac{\partial T}{\partial z} + w \frac{\partial T}{\partial r} = α [\frac{\partial^{2} T}{\partial r^{2}} + \frac{\partial T}{\partial r} \frac{1}{r}] - \frac{1}{ρ c_{p}} \frac{1}{r} \frac{\partial (r q_{r})}{\partial r} + τ [D_{B} \frac{\partial C}{\partial r} \frac{\partial T}{\partial r} + \frac{D_{T}}{T_{\infty}} {(\frac{\partial T}{\partial r})}^{2}] + \frac{Q_{0}}{ρ c_{p}} (T - T_{\infty}), (3)

concentration equation,

u \frac{\partial C}{\partial z} + w \frac{\partial C}{\partial r} = D_{B} [\frac{\partial^{2} C}{\partial r^{2}} + \frac{\partial C}{\partial r} \frac{1}{r}] + \frac{D_{T}}{T_{\infty}} [\frac{\partial T}{\partial r} \frac{1}{r} + \frac{\partial^{2} T}{\partial r^{2}}] - {k_{r}}^{2} (C - C_{\infty}) {(\frac{T}{T_{\infty}})}^{n} \exp (- \frac{E_{a}}{k_{B} T}), (4)

and gyrotactic microorganism equation,

u \frac{\partial n}{\partial z} + w \frac{\partial n}{\partial r} + \frac{b W_{c}}{(C_{w} - C_{\infty})} [\frac{\partial}{\partial r} (n \frac{\partial C}{\partial r})] = D_{m} \frac{\partial^{2} n}{\partial r^{2}} . (5)

The subjected boundary conditions (BCs) are [45, 46]

\begin{array}{c} w (r, z) = 0, u (r, z) = 2 a z, - k \frac{\partial T}{\partial r} = h (T_{f} - T), - D_{B} \frac{\partial C}{\partial r} = k (C_{f} - C), - D_{m} \frac{\partial n}{\partial r} = h (n_{f} - n) a t r = R_{1}, \\ u \to 0, C \to C_{\infty}, n \to n_{\infty}, T \to T_{\infty}, a s r \to \infty \end{array} (6)

where $D_{B}$ and $D_{T}$ are mass diffusivity and thermophoretic coefficients, $α$ is the thermal diffusivity, $D_{m}$ is the coefficient of microorganism diffusion, $W_{c}$ is the speed of the swimming cell, $g$ is the gravity, $Q_{0}$ is the heat source coefficient, $b$ is the chemotaxis constant, $K_{r}$ is the chemical reaction, $E_{a}$ is the coefficient of activation energy, and $B_{0}$ is the strength of the magnetic field.

A group of similar variables is used to obtain a dimensionless form of modeled equations (40) and(43).

u = 2 a z f^{'} (η), w = - a R_{1} \frac{f (η)}{η^{1 / 2}}, ϕ (η) = \frac{C - C_{\infty}}{C_{w} - C_{\infty}}, θ (η) = \frac{T - T_{\infty}}{T_{w} - T_{\infty}}, ξ (η) = \frac{n - n_{\infty}}{n_{w} - n_{\infty}}, η = {(\frac{r}{R_{1}})}^{2} . (7)

In light of Eq. 7, we have from Eqs 1–6

\begin{array}{l} η f^{‴} + f^{″} - β_{1} R e (\frac{1}{η} f^{″} f^{2} + 2 f^{'} f^{‴} - 4 f f^{'} f^{″}) - R e F r {f^{'}}^{2} + R e f f^{″} \\ - f^{'} (K_{1} + R e M) + λ (N_{r} φ + θ + R_{b} ξ) = 0, \end{array} (8)

(1 + R_{d}) (η θ^{″} + θ^{'}) + R e P r f θ^{'} + N_{b} \Pr η φ^{'} θ^{'} + N_{t} \Pr η {θ^{'}}^{2} = 0, (9)

η φ^{″} + φ^{'} + P r R e L e f φ^{'} + \Pr L e \frac{N_{t}}{N_{b}} θ^{'} + L e \Pr \frac{N_{t}}{N_{b}} η θ^{″} + Γ L e \Pr φ {(1 + Ω θ)}^{n} \exp (\frac{- E}{1 + Ω θ}) = 0, (10)

2 η ξ^{″} + (1 + 2 R e L_{b} f) ξ^{'} - P e [2 η ξ^{'} φ^{'} + (ξ + δ) (φ^{'} + 2 η φ^{″})] = 0 . (11)

Subjected BCs with the help of Eq. 7 become

\begin{array}{c} f (1) = 0, f^{'} (1) = 1, θ^{'} (1) = - ε_{1} (1 - θ (1)), φ (1) = 1, ξ (1) = 1 \\ f^{'} (\infty) = 0, θ (\infty) = 0, φ (\infty) = 0, ξ (\infty) = 0, \end{array} (12)

where $ε_{1} = \frac{h_{t}}{k} \sqrt{\frac{υ}{a}}$ is the Biot number.

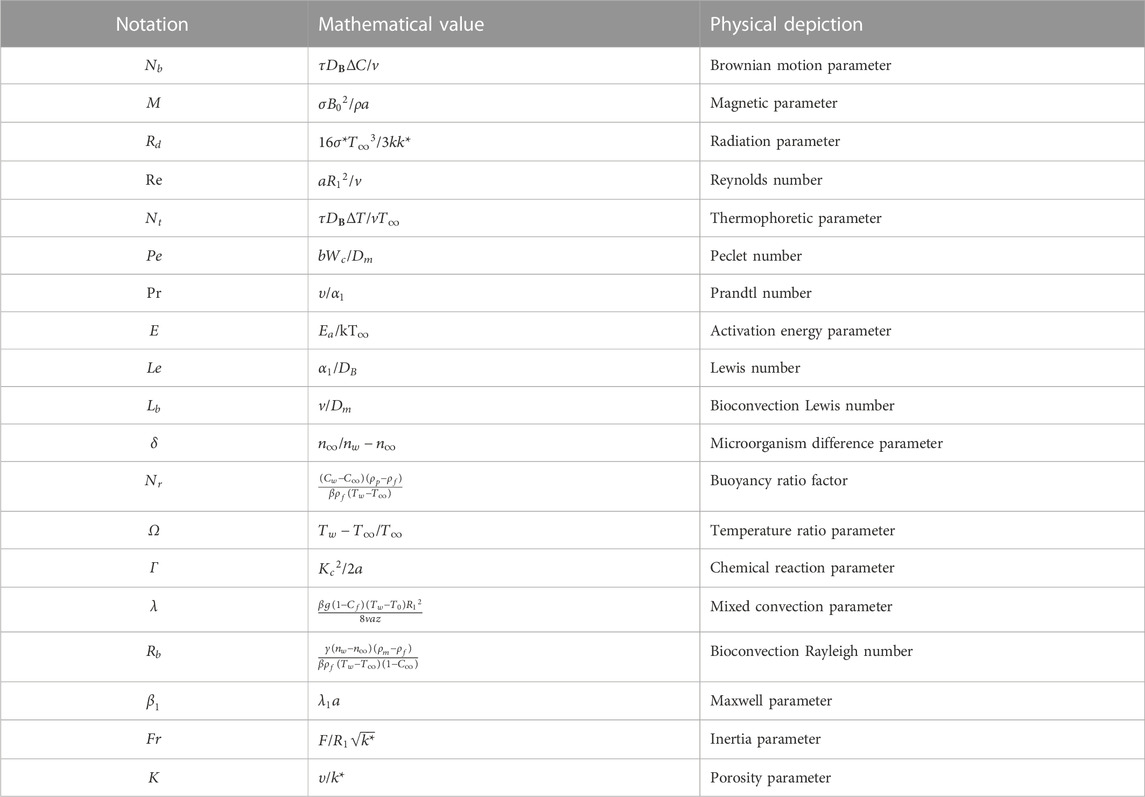
In the process of aforementioned non-dimensionalization, few physical parameters have been obtained which are described in detail in Table 1.

TABLE 1

TABLE 1. Depiction of substantial parameters.

Physical quantities

In thermodynamics, scientists and engineers are basically concerned to explore and determine the heat and mass diffusions for fluid motion. Some interested quantities are discussed as follows:

1) Nusselt number:

N u = \frac{R_{1}}{k (T_{w} - T_{\infty})} (- k) {(\frac{\partial T}{\partial r})}_{r = R_{1}} . (13)

Incorporating Eq. 7 in Eq. 13, we have

N u = - 2 θ^{'} (1) . (14)

2) Sherwood number:

S h = \frac{R_{1}}{k (C_{w} - C_{\infty})} (- D_{B}) {(\frac{\partial C}{\partial r})}_{r = R_{1}} . (15)

Substituting Eq. 7 in Eq. 15, we have

S h = - 2 ϕ^{'} (1) . (16)

3) Microorganism density number:

N n = \frac{R_{1}}{D_{m} (N_{w} - N_{\infty})} (- D_{m}) {(\frac{\partial N}{\partial r})}_{r = R_{1}} . (17)

Substituting Eq. 7 in Eq. 17, we get

N n = - 2 ξ_{n} (1) . (18)

Solution method

The governing equations have changed to dimensionless notations with suitable variables. The obtained set of dimensionless Eqs 8–11 in light of boundary conditions given in Eq. 12 will now be solved using HAM. This technique requires some initial guesses as startup values, which are given as follows:

f_{0} (η) = \frac{1}{1 + α (1 + K_{1})} (1 - e^{η}), Θ_{0} (η) = (1 - γ) e^{- η}, Φ_{0} = (1 - γ_{1}) e^{- η}, ξ (η) = (1 - γ_{2}) e^{- η} . (19)

The linear operators are as follows:

L_{f} = f^{‴} - f^{'}, L_{Θ} = θ^{″} - θ, L_{Φ} = ϕ^{″} - ϕ, L_{ξ} = ξ^{″} - ξ . (20)

Furthermore,

\begin{array}{l} L_{f} (S_{1} + S_{2} e^{η} + S_{3} e^{- η}) = 0, L_{Θ} (S_{4} e^{η} + S_{5} e^{- η}) = 0, L_{Φ} (S_{6} e^{η} + S_{7} e^{- η}) = 0, \\ L_{ξ} (S_{8} e^{η} + e S_{9} e^{- η}) = 0, \end{array} (21)

where $S_{i}$ for $i = 1,2,3 . . . . . . . 9$ are fixed values.

\begin{array}{l} Ν_{\overset{⌢}{f}} [\overset{⌢}{f} (η; ξ), \overset{⌢}{θ} (η; ξ), \overset{⌢}{ϕ} (η; ξ), \overset{⌢}{ξ} (η; ξ)] = {\overset{⌢}{f}}_{η η} + η {\overset{⌢}{f}}_{η η η} - β_{1} R e (\frac{1}{η} {(\overset{⌢}{f})}^{2} {\overset{⌢}{f}}_{η η} + 2 {\overset{⌢}{f}}_{η} {\overset{⌢}{f}}_{η η η} - 4 \overset{⌢}{f} {\overset{⌢}{f}}_{η} {\overset{⌢}{f}}_{η η}) \\ - R e {({\overset{⌢}{f}}_{η})}^{2} + R e \overset{⌢}{f} {\overset{⌢}{f}}_{η η} - (K_{1} + R e M) {\overset{⌢}{f}}_{η} + λ (\overset{⌢}{θ} + N_{r} \overset{⌢}{φ} + R_{b} \overset{⌢}{ξ}), \end{array} (22)

Ν_{\overset{⌢}{θ}} [\overset{⌢}{f} (η; ξ), \overset{⌢}{θ} (η; ξ), \overset{⌢}{ϕ} (η; ξ), \overset{⌢}{ξ} (η; ξ)] = (1 + R_{d}) (η {\overset{⌢}{θ}}_{η η} + {\overset{⌢}{θ}}_{η}) + P r R e \overset{⌢}{f} {\overset{⌢}{θ}}_{η} + N_{b} \Pr η {\overset{⌢}{ϕ}}_{η} {\overset{⌢}{θ}}_{η} + N_{t} η \Pr {({\overset{⌢}{θ}}_{η})}^{2}, (23)

\begin{array}{l} Ν_{\overset{⌢}{ϕ}} [\overset{⌢}{f} (η; ξ), \overset{⌢}{θ} (η; ξ), \overset{⌢}{ϕ} (η; ξ), \overset{⌢}{ξ} (η; ξ)] = η {\overset{⌢}{ϕ}}_{η η} + {\overset{⌢}{ϕ}}_{η} + P r L e (R e \overset{⌢}{f} {\overset{⌢}{ϕ}}_{η} + \frac{N_{t}}{N_{b}} {\overset{⌢}{θ}}_{η η}) \\ + L e \Pr Γ \overset{⌢}{ϕ} {(1 + Ω \overset{⌢}{θ})}^{n} \exp (\frac{- E}{1 + Ω \overset{⌢}{θ}}), \end{array} (24)

\begin{array}{l} Ν_{\overset{⌢}{ξ}} [\overset{⌢}{f} (η; ξ), \overset{⌢}{θ} (η; ξ), \overset{⌢}{ϕ} (η; ξ), \overset{⌢}{ξ} (η; ξ)] = 2 η {\overset{⌢}{ξ}}_{η η} + (1 + 2 R e L_{b} \overset{⌢}{f}) {\overset{⌢}{ξ}}_{η} \\ - P e [2 η {\overset{⌢}{ξ}}_{η} {\overset{⌢}{ϕ}}_{η} + (δ + \overset{⌢}{ξ}) ({\overset{⌢}{ϕ}}_{η} + 2 η {\overset{⌢}{ϕ}}_{η η})] . \end{array} (25)

The 0-order description for Eqs 8–11 is given as follows:

(1 - ζ) L_{\overset{⌢}{f}} [\overset{⌢}{f} (η; ζ) - {\overset{⌢}{f}}_{0} (η)] = ζ ℏ_{\overset{⌢}{f}} Ν_{\overset{⌢}{f}} [\overset{⌢}{f} (η; ξ), \overset{⌢}{θ} (η; ξ), \overset{⌢}{ϕ} (η; ξ), \overset{⌢}{ξ} (η; ξ])], (26)

(1 - ζ) L_{\overset{⌢}{θ}} [\overset{⌢}{θ} (η; ζ) - {\overset{⌢}{θ}}_{0} (η)] = ζ ℏ_{\overset{⌢}{θ}} Ν_{\overset{⌢}{θ}} [\overset{⌢}{f} (η; ξ), \overset{⌢}{θ} (η; ξ), \overset{⌢}{ϕ} (η; ξ), \overset{⌢}{ξ} (η; ξ)], (27)

(1 - ζ) L_{\overset{⌢}{ϕ}} [\overset{⌢}{ϕ} (η; ζ) - {\overset{⌢}{ϕ}}_{0} (η)] = ζ ℏ_{\overset{⌢}{ϕ}} Ν_{\overset{⌢}{ϕ}} [\overset{⌢}{f} (η; ξ), \overset{⌢}{θ} (η; ξ), \overset{⌢}{ϕ} (η; ξ), \overset{⌢}{ξ} (η; ξ)], (28)

(1 - ζ) L_{\overset{⌢}{ξ}} [\overset{⌢}{ξ} (η; ζ) - {\overset{⌢}{ξ}}_{0} (η)] = ζ ℏ_{\overset{⌢}{ξ}} Ν_{\overset{⌢}{ξ}} [\overset{⌢}{f} (η; ξ), \overset{⌢}{θ} (η; ξ), \overset{⌢}{ϕ} (η; ξ), \overset{⌢}{ξ} (η; ξ)] . (29)

Related conditions are as follows:

\begin{array}{l} {\overset{⌢}{f} (η; ζ)|}_{η = 1} = 0, {\frac{\partial \overset{⌢}{f} (η; ζ)}{\partial η}|}_{η = 1} = 1, {\overset{⌢}{θ} (η; ζ)|}_{η = 1} = - ε_{1} (1 - \overset{⌢}{θ} (1)), {\overset{⌢}{ϕ} (η; ζ)|}_{η = 1} = 1, \overset{⌢}{ξ} {(η; ζ)|}_{η = 1} = 1 \\ {\frac{\partial \overset{⌢}{f} (η; ζ)}{\partial η}|}_{η \to \infty} = 0, {\overset{⌢}{ϕ} (η; ζ)|}_{η \to \infty} = 0, \overset{⌢}{ξ} {(η; ζ)|}_{η \to \infty} = 0, {\overset{⌢}{θ} (η; ζ)|}_{η \to \infty} = 0, \end{array} (30)

such that $ζ \in [0, 1]$ , so for $ζ = 0 a n d ζ = 1$ , we have

\overset{⌢}{f} (η; 1) = \overset{⌢}{f} (η), \overset{⌢}{θ} (η; 1) = \overset{⌢}{θ} (η), \overset{⌢}{ξ} (η; 1) = \overset{⌢}{ξ} (η), \overset{⌢}{ϕ} (η; 1) = \overset{⌢}{ϕ} (η) . (31)

The Taylor’s series expansion for $\overset{⌢}{f} (η; ζ), \overset{⌢}{θ} (η; ζ), \overset{⌢}{ϕ} (η; ζ), a n d \overset{⌢}{ξ} (η; ζ)$ around $ζ = 0$

\begin{array}{l} \overset{⌢}{f} (η; ζ) = {\overset{⌢}{f}}_{0} (η) + \sum_{n = 1}^{\infty} {\overset{⌢}{f}}_{n} (η) ζ^{n}, \\ \overset{⌢}{ϕ} (η; ζ) = {\overset{⌢}{ϕ}}_{0} (η) + \sum_{n = 1}^{\infty} {\overset{⌢}{ϕ}}_{n} (η) ζ^{n}, \\ \overset{⌢}{θ} (η; ζ) = {\overset{⌢}{θ}}_{0} (η) + \sum_{n = 1}^{\infty} {\overset{⌢}{θ}}_{n} (η) ζ^{n}, \\ \overset{⌢}{ξ} (η; ζ) = {\overset{⌢}{ξ}}_{0} (η) + \sum_{n = 1}^{\infty} {\overset{⌢}{ξ}}_{n} (η) ζ^{n}, \end{array} (32)

\begin{array}{c} {\overset{⌢}{f}}_{n} (η) = {\frac{1}{n!} \frac{\partial \overset{⌢}{f} (η; ζ)}{\partial η}|}_{p = 0}, {\overset{⌢}{θ}}_{n} (η) = {\frac{1}{n!} \frac{\partial \overset{⌢}{θ} (η; ζ)}{\partial η}|}_{p = 0}, \\ {\overset{⌢}{ϕ}}_{n} (η) = {\frac{1}{n!} \frac{\partial \overset{⌢}{ϕ} (η; ζ)}{\partial η}|}_{p = 0}, {\overset{⌢}{ξ}}_{n} (η) = {\frac{1}{n!} \frac{\partial \overset{⌢}{ξ} (η; ζ)}{\partial η}|}_{p = 0} . \end{array} (33)

Related BCs are as follows:

\begin{array}{l} \overset{⌢}{f} (1) = 0, \overset{⌢}{f}' (1) = 1, \overset{⌢}{θ}' (1) = - ε_{1} (1 - \overset{⌢}{θ} (1)), \overset{⌢}{ϕ} (1) = 1, \overset{⌢}{ξ} (1) = 1, \\ \overset{⌢}{f}' (\infty) = 0, \overset{⌢}{θ} (\infty) = 0, \overset{⌢}{ϕ} (\infty) = 0, \overset{⌢}{ξ} (\infty) = 0 . \end{array} (34)

Then, we have

\begin{array}{l} R_{n}^{\overset{⌢}{f}} (η) = η {\overset{⌢}{f}}_{n - 1} ‴ + {\overset{⌢}{f}}_{n - 1} ″ - β_{1} R e (\frac{1}{η} {({\overset{⌢}{f}}_{n - 1})}^{2} {\overset{⌢}{f}}_{n - 1} ″ + 2 {\overset{⌢}{f}}_{n - 1}' {\overset{⌢}{f}}_{n - 1} ‴ - 4 \overset{⌢}{f} \sum_{j = 0}^{w - 1} {\overset{⌢}{f}}_{w - 1 - j} {\overset{⌢}{f}}_{j} ″) \\ - R e {({\overset{⌢}{f}}_{n - 1}')}^{2} + R e \overset{⌢}{f} \sum_{j = 0}^{w - 1} {\overset{⌢}{f}}_{w - 1 - j} {\overset{⌢}{f}}_{j} ″ - (K_{1} + R e M) {\overset{⌢}{f}}_{n - 1}' + λ ({\overset{⌢}{θ}}_{n - 1} + N_{r} {\overset{⌢}{φ}}_{n - 1} + R_{b} {\overset{⌢}{ξ}}_{n - 1}), \end{array} (35)

R_{n}^{\overset{⌢}{θ}} (η) = (1 + R_{d}) ({\overset{⌢}{θ}}_{n - 1} ″ + {\overset{⌢}{ϕ}}_{n - 1}') + \Pr (R e \sum_{j = 0}^{w - 1} {\overset{⌢}{θ}}_{n - 1}' {\overset{⌢}{f}}_{w - 1 - j} + η (N_{b} {\overset{⌢}{θ}}_{n - 1}' {\overset{⌢}{ϕ}}_{n - 1}' + N_{t} {({\overset{⌢}{θ}}_{n - 1}')}^{2})), (36)

R_{n}^{\overset{⌢}{ϕ}} (η) = η {\overset{⌢}{ϕ}}_{n - 1} ″ + {\overset{⌢}{ϕ}}_{n - 1}' + \Pr L e (R e \overset{⌢}{f} {\overset{⌢}{ϕ}}_{η - 1} + \frac{N_{t}}{N_{b}} {\overset{⌢}{θ^{″}}}_{n - 1}) + L e \Pr Γ {(1 + Ω \overset{⌢}{θ})}^{n} \exp (\frac{- E}{1 + Ω \overset{⌢}{θ}}) \sum_{j = 0}^{w - 1} ϕ_{w - 1 - j}, (37)

R_{n}^{\overset{⌢}{ξ}} (η) = 2 η {\overset{⌢}{ξ}}_{n - 1} ″ + \sum_{j = 0}^{w - 1} (1 + 2 R e L_{b} {\overset{⌢}{f}}_{j}) {\overset{⌢}{ξ}}_{w - 1 - j}' - P e (\sum_{j = 0}^{w - 1} {\overset{⌢}{ξ}}_{w - 1 - j}' {\overset{⌢}{ϕ}}_{j} + \sum_{j = 0}^{w - 1} (δ + {\overset{⌢}{ξ}}_{w - 1 - j}) ({\overset{⌢}{ϕ}}_{n - 1}' + 2 η {\overset{⌢}{ϕ}}_{n - 1} ″)), (38)

{M o r e o v e r, w e h a v e ξ}_{n} = \{\begin{array}{c} 0, & i f ζ \leq 1 \\ 1, & i f ζ > 1 . \end{array} (39)

Discussion of results

This work examines the effects of the bioconvection Maxwell nanofluid flow over a stretching and revolving cylinder that is inserted in a permeable medium. The thermophoretic and Brownian motion characteristics due to the nanofluid flow are captured by implementing the Buongiorno model. The core importance of this study is to explore and improve the thermal and mass transmission for the flow system. The influence of various parameters with numerical values $N r = 0.1, K_{1} = 0.2, R e = 0.03, β_{1} = 0.1, λ = 0.2,$ R_b = 0.1, N_b = 0.2, N_t = 0.2, R_d = 0.1, Fr = 0.01, Le = 0.4, Γ = 0.5, Ω = 0.5, L_b = 0.1, δ = 0.2, Pe = 0.1, M = 0.3, Pr = 21 on fluid flow will be described theoretically with the help of graphical view in the upcoming paragraphs.

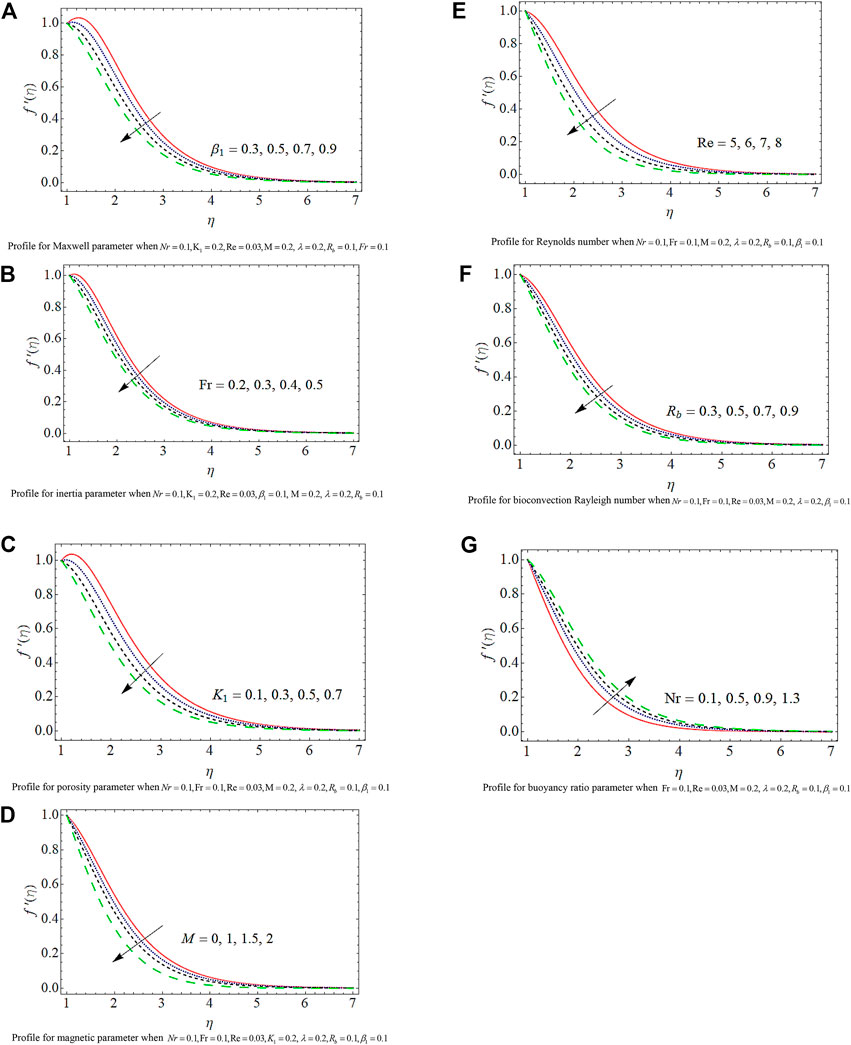
Figure 2 describes the effect of different parameters on the velocity of the fluid. Figure 2A depicts that augmenting values of the Maxwell parameter $β_{1}$ declines fluid flow. Basically, the growing values of $β_{1}$ enhance the stress relaxation phenomenon, which drops down the flow characteristics, as depicted in Figure 2A. From Figure 2B, it has been noticed that the inertia coefficient or Forchheimer number $F r$ has an adverse impact upon the velocity of the fluid. The upper values of $F r$ cause a decline in the flow profile. Since an augmentation in $F r$ causes the generation of higher resistive or drag forces to the flow of the fluid, this physical phenomenon results in a decline in the profile of fluid flow. The motion of fluid, as depicted in Figure 2C, reduces for a growth in the porosity parameter $K_{1}$ . For growth in $K_{1}$ , the void spaces in the medium increase, and this offers more conflict to the fluid motion and gradually causes a decline in the flow profiles. Figure 2D portrays the magnetic impacts $M$ upon flow. The Lorentz force is generated for augmenting the values of $M$ , which offers a resistance to the flow and causes reduction in the flow characteristics. Therefore, the magnetic effect significantly monitors the flow behavior of fluid particles. Figure 2E depicts the impact of the Reynolds number $R e$ upon the flow profile. The inertial force is a conflicting agent to the flow of fluid particles, where this inertial force within the fluid particles becomes dominant with a growth in $R e$ , which opposes the fluid motion. Hence, the augmenting values of $R e$ reduce the flow profile, as presented in Figure 2E. The impact of the bioconvection number $R_{b}$ is depicted in Figure 2F. Physically, an augmentation in $R_{b}$ creates a contrasting force to the fluid particles in the direction of motion that leads to a reduction in the flow profile. Figure 2G depicts that strength of the momentum boundary layer rises up with enhancing values of $N_{r}$ . Hence, the velocity profile grows up for higher values of $N_{r}$ .

FIGURE 2

FIGURE 2. Flow profiles under the impact of various substantial parameters.

Figure 3A portrays the influence of $N_{b}$ upon the thermal profile. Physically, when the values of $N_{b}$ increase higher, then the haphazard flow of fluid particles also increases for which the collision among the fluid particles increases. In this phenomenon, kinetic energy of the fluid particles is changed to thermal energy, which results ultimately in augmentation in the thermal characteristics of particles. The effect of the thermophoretic parameter $N_{t}$ upon heat flow is depicted in Figure 3B. From this figure, it has been revealed that, for an upsurge in $N_{t}$ , there is a higher difference in the temperature that will lead to a growth in the temperature flow from a warmer region to a colder region. This physical phenomenon results in augmentation in the temperature of the fluid. Figure 3C endorses that thermal diffusion is supported by a growth in the radiation parameter $R_{d}$ . Physically, an augmentation in $R_{d}$ increases the size of the thermal boundary layer and diffuses more heat. Hence, the higher values of $R_{d}$ provide maximum temperature to the flow system. Figure 3D illustrates the effect of Reynolds number $R e$ on the thermal profile. It is obvious from this figure that more thermal flow occurs for growth in $R e$ . The fluid’s convective force declines for augmentation in $R e$ , which boosts up the thermal boundary layer wideness and causes a growth in temperature.

FIGURE 3

FIGURE 3. Temperature profiles under the impact of various substantial parameters.

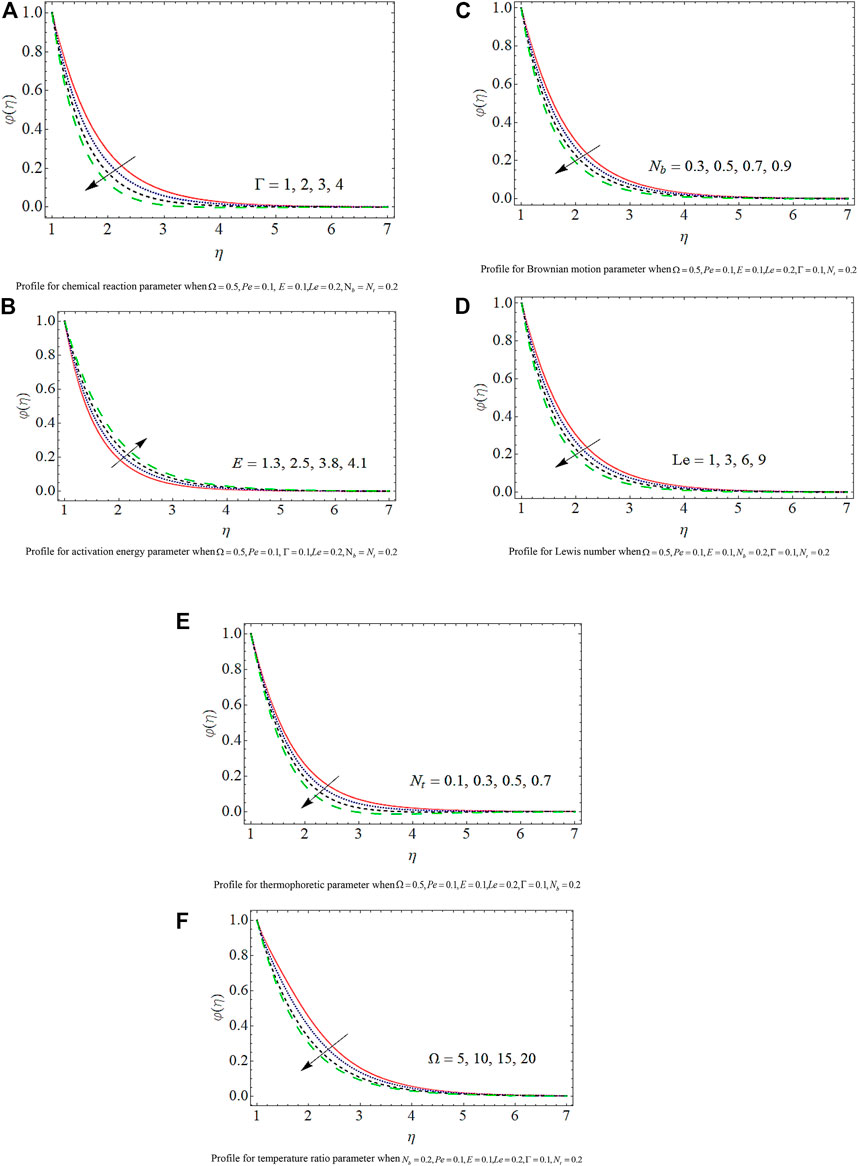
Figure 4 shows the influence of different physical parameters over concentration. Figure 4A portrays that the width of the concentration border line declines with the augmenting values of the chemical reaction parameter $Γ$ . With the augmentation in $Γ$ , the fluid molecular diffusivity shrinks, for which less mass transfer occurs. In this phenomenon, the concentration of the fluid drops down as values of $Γ$ increase. With the augmentation in the activation energy factor $E$ , the concentration characteristics increase, as depicted in Figure 4B. Physically, the number of fluid molecules with a requirement of small energy is enhanced for growing values of $E$ , which result in more mass diffusion. Figure 4C shows that with the augmentation in $N_{b}$ , the concentration profiles upsurge. When $N_{b}$ increases, then the random collision among the fluid particles also increases, which leads to a reduction in mass transfer. Hence, growth in $N_{b}$ resembles a decline in the concentration characteristics. The impact of Lewis number upon mass flow is depicted in Figure 4D. With the growth in $L e$ , the mass flow declines that weakens the concentration characteristics. Mass flow is also depreciated with the augmentation in $N_{t}$ , as depicted in Figure 4E. The thermal conductivity of the fluid improves with the progression in $N_{t}$ that weakens the strength of the concentration boundary layer, due to which less mass transmission takes place. Figure 4F depicts that concentration is a reducing function of the temperature ratio parameter $Ω$ . Since the growing values of $Ω$ result in an augmentation in the temperature difference that leads to more thermal flow at the free stream. In this physical phenomenon, the mass flow in the closed neighborhood of the cylinder reduces, which declines the concentration. Hence, growth in the values of $Ω$ corresponds to a decline in the concentration, as shown in Figure 4F.

FIGURE 4

FIGURE 4. Concentration profiles under the impact of various substantial parameters.

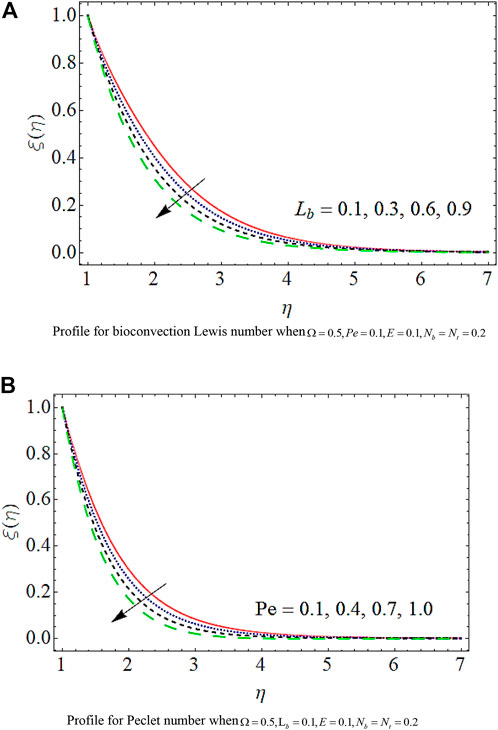
The impact upon the density of motile microorganisms for variations in $L_{b}$ and $P e$ is described in Figure 5. This figure confirms that the density of microorganism declines with the growth in $L_{b}$ and $P e$ . The augmenting values of $L_{b}$ cause degeneration in the motile microorganism density, which leads to reduction in the distribution of motile microorganisms, as shown in Figure 5A. The Peclet number $P e$ is closely related to microorganism diffusivity. It is observed that the greater values of $P e$ cause a decline in diffusion of motile microorganisms. Hence, augmenting values of $P e$ decline the profile for motile microorganisms, as presented in Figure 5B. Figures 6A–D display the magnetic effects $M$ in the form of streamlines. The variations in streamlines have been rapidly shown with the increasing amount of the magnetic parameter.

FIGURE 5

FIGURE 5. Motile microorganism profiles under the impact of different parameters.

FIGURE 6

FIGURE 6. (A–D): Impact of the magnetic field on streamlines when $F r = 0.1, λ = 0.2, R_{b} = 0.1, β_{1} = 0.1 .$

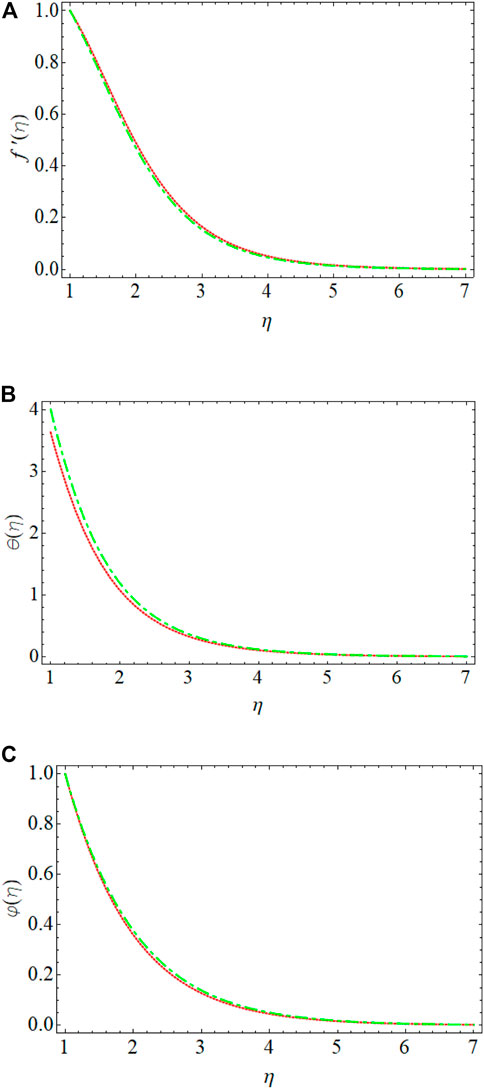
Figures 7A–C depict the authentication of this work. In this figure, the current results are endorsed with the established work given by Ahmed et al. [42] by taking the common factors. This figure recommends a closed settlement between the published and current work.

FIGURE 7

FIGURE 7. (A–C) Validation of the current work with established results.

Discussion of tables

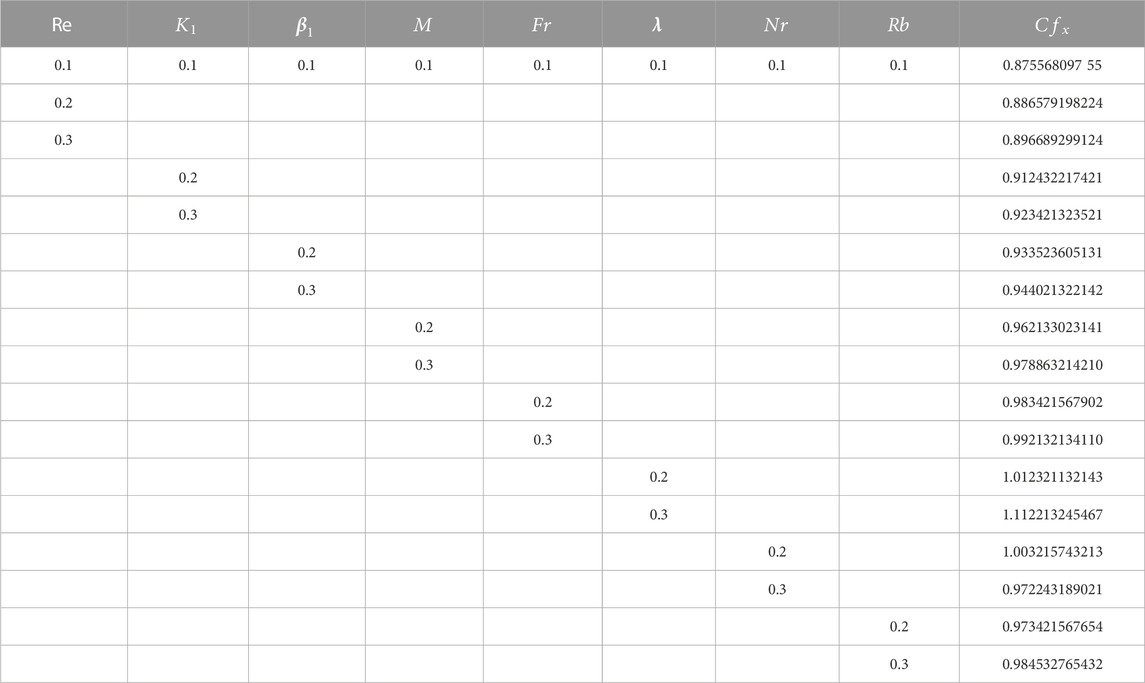
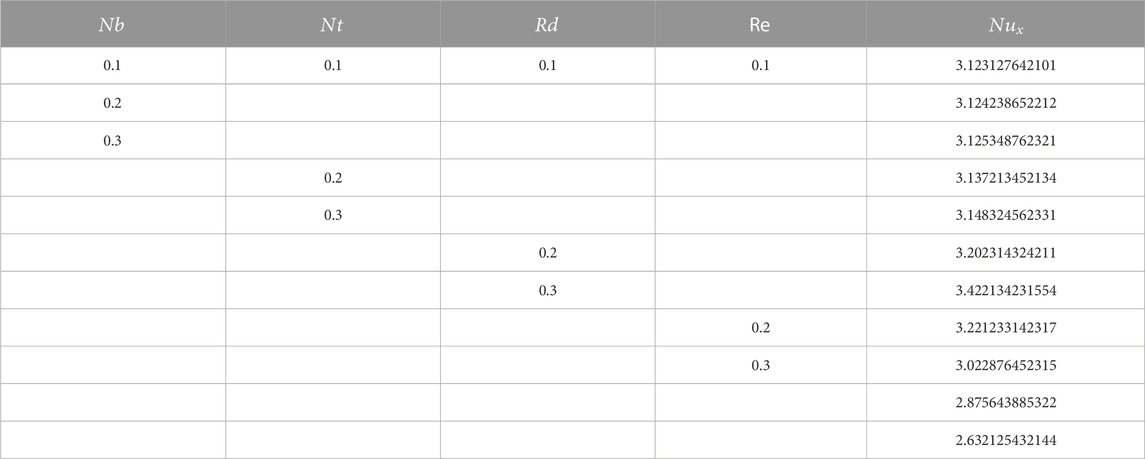
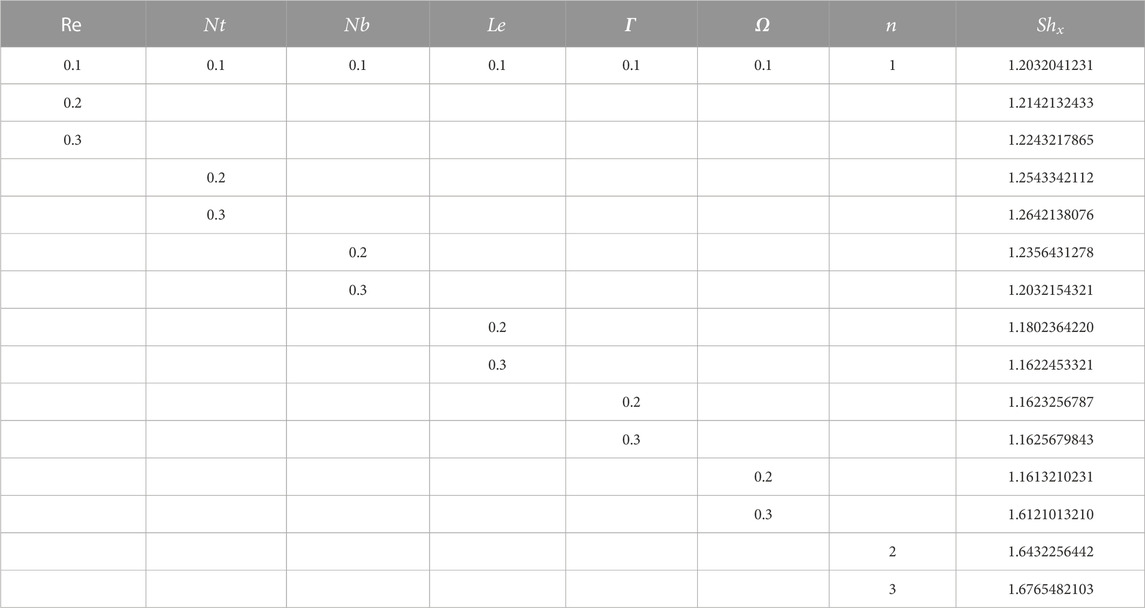
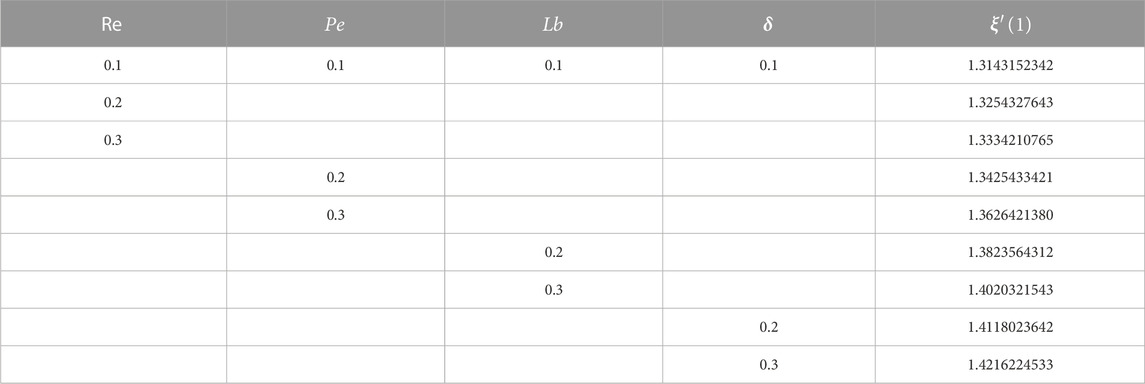
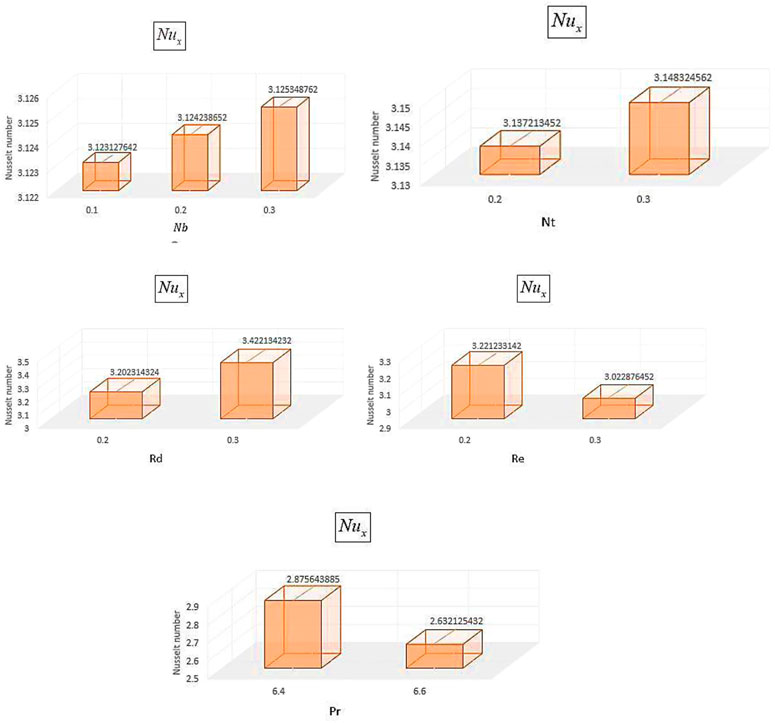
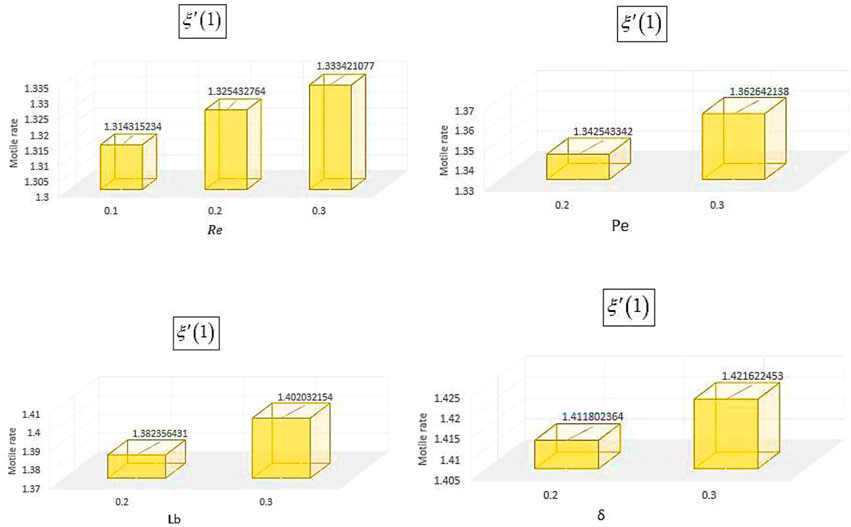
The impact of different emerging factors over interested quantities has been numerically described in Table 2, Table 3, Table 4, and Table 5. Table 2 portrays that the skin friction grows up in response to the resistive force produced by the augmenting values of the Maxwell parameter, inertia coefficient, porosity parameter, magnetic parameter, Reynolds number, and bioconvection Rayleigh number, while it decays with the growth in the buoyancy ratio parameter. The statistical calculations for skin friction in response to different parameters are presented in Chart 1. Table 3 portrays that the heat flow rate upsurges for augmentation in Brownian motion, thermophoretic parameter, Reynolds number, and radiation parameter. The thermal flow rate vs. different parameters is statistically given in Chart 2. The mass flow rate is supported by the growth in the activation energy parameter, while it is opposed by the augmentation in the chemical parameter, Lewis number, thermophoretic parameter, and temperature ratio parameter, as depicted numerically in Table 4. The density number of microorganisms is declined by a growth in the values of Peclet and bioconvective Lewis numbers, as presented in Table 5, while its statistical calculations are presented in Chart 3.

TABLE 2

TABLE 2. Skin friction $C_{f x} R {e_{x}}^{0.5}$ vs. various parameters for the Maxwell nanofluid.

TABLE 3

TABLE 3. Nusselt number $N u_{x} R {e_{x}}^{- 0.5}$ against numerous factors.

TABLE 4

TABLE 4. Sherwood number against different factors for the Maxwell nanofluid.

TABLE 5

TABLE 5. Motile rate vs. the embedded parameters for the Maxwell nanofluid.

CHART 1

CHART 1. Statistical calculation for skin friction $C_{f x} R {e_{x}}^{0.5}$ against numerous factors.

CHART 2

CHART 2. Statistical calculation for the Nusselt number $N u_{x} R {e_{x}}^{- 0.5}$ against numerous factors.

CHART 3

CHART 3. Statistical calculation for the motile rate $ξ^{'} (1)$ vs. various parameters

Conclusion

This work determines the bioconvection Maxwell nanofluid flow over a stretching and revolving cylinder that is inserted in a permeable medium. The main focus of this work is to explore and improve thermal and mass transmission for the flow system. The thermophoretic and Brownian motion characteristics due to the nanofluid flow are captured by implementing the Buongiorno model. After deep inspection of the current study, the following main points are concluded:

1) With the growth in values of the Maxwell parameter, inertia coefficient, bioconvection number, porosity parameter, magnetic parameter, and Reynolds number, there is a reduction in flow characteristics.

2) The motion of fluid grows up with the augmenting values of the buoyancy parameter, which leads to an augmentation in the velocity profiles.

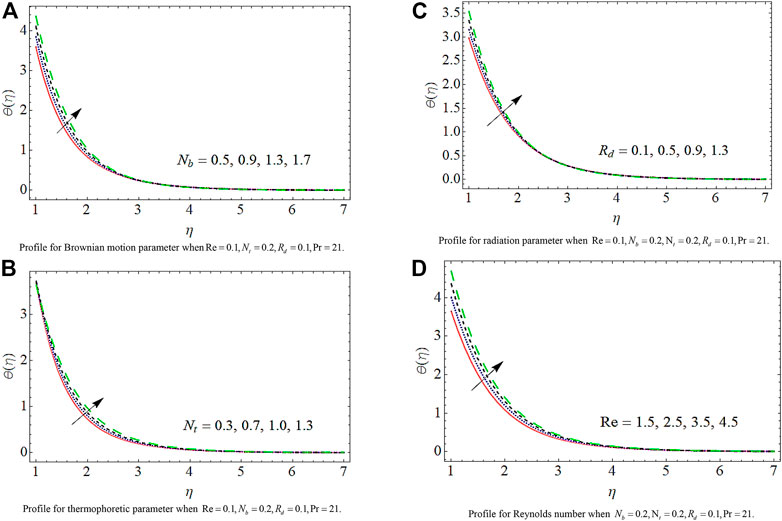
3) The rising values of Brownian motion and thermophoretic factors support the thermal flow and oppose the mass flow.

4) The growth in the radiation parameter and Reynolds number causes an augmentation in the temperature of the fluid.

5) With the augmenting values of the chemical reaction, the fluid molecular diffusivity reduces, due to which less mass diffuses, which causes a decline in the concentration of the fluid. On the other hand, with the augmenting values of the activation energy factor, the concentration profiles grow up.

6) For growth in Lewis and Prandtl numbers, there is a decline in the mass flow that results in a decay in the concentration profile.

7) The growth in the temperature ratio results in an augmentation in the temperature difference that leads to more thermal flow at free stream due to which the diffusivity of mass in the closed vicinity of the cylinder reduces and weakens the concentration profile.

8) An augmentation in the Peclet number leads to a decline in the diffusivity of motile microorganisms that declines the profile for microorganisms.

9) The statistical data for the enhancement in skin friction, Nusselt number, and motile microorganisms due to various parameters are shown in Chart 1, 2, and 3, respectively.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AK modeled the problem. AK and ZI wrote the manuscript. AK and SE solved the modeled problem by the homotopy analysis method.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University (KKU) for funding this research project Number (RGP.1/44/43). The author Somia Awad (Ssawad@uqu.edu.sa) would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (22UQU4340602DSR01), Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R163), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Platt JR. Bioconvection patterns in cultures of free-swimming organisms. Science (1961) 133(3466):1766–7. doi:10.1126/science.133.3466.1766

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Ahmad I, Aziz S, Ali N, Khan SU, Khan MI, Tlili I, et al. Thermally developed Cattaneo-Christov Maxwell nanofluid over bidirectional periodically accelerated surface with gyrotactic microorganisms and activation energy. Alexandria Eng J (2020) 59(6):4865–78. doi:10.1016/j.aej.2020.08.051

ORIGINAL RESEARCH article

Bioconvection Maxwell nanofluid flow over a stretching cylinder influenced by chemically reactive activation energy surrounded by a permeable medium

Introduction

Novelty/originality

Physical and mathematical description

Physical quantities

Solution method

Discussion of results

Discussion of tables

Conclusion

Data availability statement

Author contributions

Acknowledgments

Conflict of interest

Publisher’s note

References

Nomenclature

Greek symbols

Abbreviations

People also looked at