Modeling and Multi-Objective Optimization of Thermophysical Parameters of Hybrid Nanodiamond–Ni-Based Nanofluids via Response Surface Methodology

Introduction

Nanofluids are emerging heat transfer fluids that perform essential functions in many process industries. Although these fluids are widely used in several heat transfer applications, their thermal conductivity is considerably low. It has been proven by recent advancements in nanofluid technology that the thermal conductivity of these fluids can be drastically increased by adding nanoparticles. The enhancement in the thermophysical properties has gained tremendous attention from researchers (Ahmadi et al., 2018; Qiu et al., 2020; Tung et al., 2020). Nano-sized particle-based fluids called nanofluids have shown promising results in several thermal management applications. It is a prominent fact that the addition of nanoparticles in conventional liquid alters all types of properties including viscosity, heat transfer coefficient, heat capacity, and density (Elsheikh et al., 2018; Kotia et al., 2018; Xian et al., 2019).

Nanodiamond-based nanofluids have gained tremendous attention from many research groups due to their exceptional mechanical, thermal, and electrical characteristics (Alshayji et al., 2020; Ilyas et al., 2020). Due to the strong covalent bonding of carbon–carbon and low phonon dispersal, diamond has the highest thermal conductivity of all nanomaterials that are conventionally used in nanofluid technology (Mashali et al., 2019). Hybrid nanofluids, which contain more than one nanoparticle type, have been utilized in many recent studies to take advantage of their integrated material properties. Moreover, adding a magnetic nanoparticle to nanodiamond-based fluids could enhance the thermophysical properties by an external magnetic field (Sundar et al., 2014a). In an experimental study by Sundar et al. (2018), the thermophysical properties of hybrid nanodiamond–Ni-based nanofluids were investigated. The thermal conductivity and viscosity enhancements were observed to be 29.39 and 23.24%, respectively, at 0.3% volume concentration of the hybrid nanofluid at 60°C compared to distilled water.

The thermophysical properties are greatly influenced by the temperature and weight percentage of nanoparticles (Hamzah et al., 2017). The optimum values of temperature and weight percentage of the nanoparticle can provide an economical solution for industrial applications. Improvements in the thermo-mechanical characteristics of fluids have emerged as an interesting outcome considering the impact of temperature and nanomaterial concentration. Finding the optimum concentration of such nano-enhanced nanofluids is crucial for economical operation since the price of nanomaterials is relatively higher than the conventional liquids, and the agglomeration can impact settling at high concentrations. The increase in the weight fraction of nanomaterial causes a substantial increase in the viscosity of the system. The increase in viscosity may increase the pumping power of the liquid, hence negatively affecting the heat transfer operation (Ali et al., 2021). Therefore, an optimization investigation is pivotal in estimating the appropriate and economical solution for thermal management.

Response surface methodology (RSM) is a straightforward and effective tool for modeling and optimization (Hemmat Esfe et al., 2019; Saxena et al., 2019; Danish et al., 2020). RSM is a statistical technique that gives the individual and combined interaction of input and output parameters in the developed model. Various studies have been performed to optimize the thermophysical properties of nanofluids, and several studies that address the use of RSM in the thermophysical optimization of nanofluids are available (Saxena et al., 2019; Hemmat Esfe et al., 2021; Rostami et al., 2021). However, the application of optimization and modeling of multi-objective parameters of hybrid nanodiamond–Ni-based nanofluid via RSM has not been subjected to investigation yet. Moreover, the present research is promising for the use of nanofluids in heat transfer applications. Therefore, the objective function was chosen based on the heat transfer enhancement at optimum temperature and nanomaterial weight percent, considering thermal conductivity as viscosity as output functions.

This investigation aims to find an optimum viscosity and thermal conductivity of nanodiamond–Ni-based nanofluids using experimental data. The polynomial functions were modeled to establish a relationship between the input parameters and output properties of nanofluids, i.e., viscosity and thermal conductivity. Then, the optimal response was estimated using the optimization methodology with the objective of increasing thermal conductivity and reducing the viscosity of nanofluids. Different testing analyses were performed to study the performance, sensitivity, and desirability of the applied RSM architecture.

Materials and Methodology

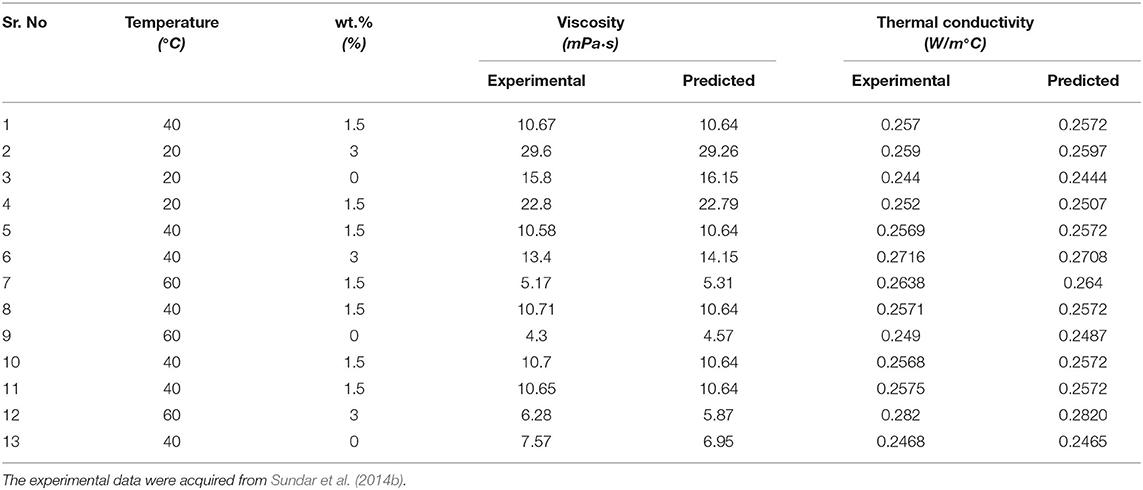
The nanofluid under investigation consisted of a new type of magnetic hybrid composite of nanodiamond and nickel (Ni) nanoparticles dispersed in ethylene glycol. The detailed procedure of the formulation of nanodiamond–Ni hybrid nanofluids can be found in the reported literature (Sundar et al., 2014b). The nanofluid samples were prepared using ultrasonication and aqueous dispersant. The nanofluids were prepared in different weight percentages, i.e., 0 (ethylene glycol), 1.5, and 3 wt.%. The thermal conductivity and viscosity of the stable nano-dispersions were subjected to investigation experimentally at varying temperatures, i.e., 20–60°C.

Response surface methodology was used to develop the model using two input parameters, i.e., temperature and weight percentage of the nanodiamond–Ni hybrid nanofluids, and two responses, i.e., thermal conductivity and viscosity. The experimental data used in this study were obtained from Sundar et al. (2014b). The detailed procedure of using the RSM can be found in the literature (Hemmat Esfe et al., 2020). A face-centered central composite design with six face-centered, six centers, and eight corner points was used. It was used to study the effect of the most and least dominant factors on thermal conductivity and viscosity. The overall flowchart of the RSM optimization methodology can be found in the literature (Hemmat Esfe and Hajmohammad, 2017).

The outcomes of this research are divided into three sections. First, the design of the experiment (DoE) was applied to model the thermal conductivity and viscosity values. In the next step, ANOVA was utilized to find the polynomial relationship between the thermal conductivity and viscosity of nanodiamond–Ni hybrid nanofluids. Then, the optimization methodology was applied based on the objective functions, optimization cases, limits, and weight, to find the optimum condition for thermal management applications. The nanodiamond–Ni hybrid nanofluid is a magnetic nanofluid, which may have potential applications, other than heat transfer, in several engineering fields involving magnetic resonance imaging and optics.

Results and Discussion

The experimental dataset from the literature (Sundar et al., 2014b) was utilized for the process variables and the responses of the model. The DoE for the process variables (temperature and wt.%) and their respective responses (thermal conductivity, viscosity) is given in Table 1.

Table 1. DoE results according to the applied optimization architecture.

Viscosity (μ) and Thermal Conductivity (k) Models

The first step involves developing a model that establishes a relationship between temperature, wt.%, thermal conductivity, and viscosity. The second step consists of the use of ANOVA for the optimization. A model was developed for the viscosity and is given as Equation (1), where temperature and wt.% are represented by A and B, respectively.

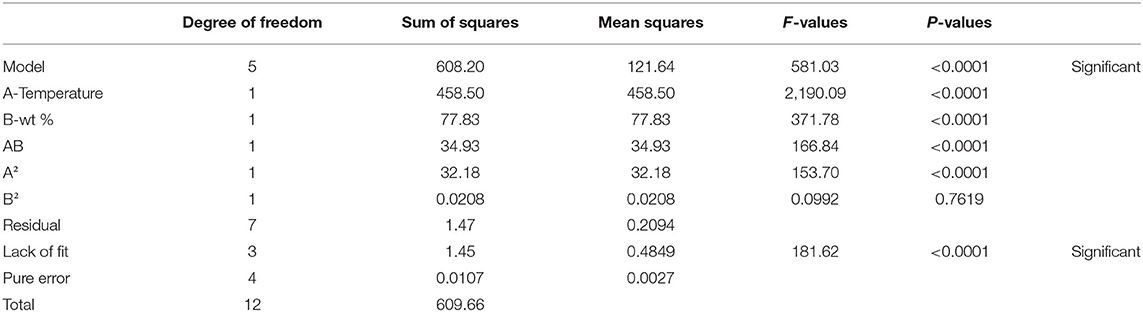
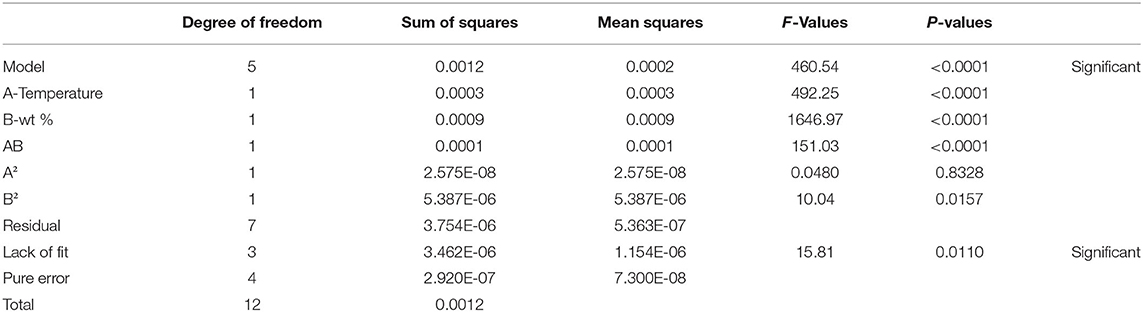
The ANOVA was applied to the model to examine the significance of all input parameters and the model itself. The input is considered significant if the P-value corresponding to the F-value is less than 0.05. If the P-value is higher than 0.5, the model will be considered insignificant. The results for the thermal conductivity model are given in Table 2. The results showed that the P-value of the model is <0.0001, proving that the model is significant.

Table 2. ANOVA results for viscosity.

Similarly, a predictive model for thermal conductivity was also developed which is shown by Equation (2) where temperature and wt. % are represented by A and B, respectively.

The ANOVA results for thermal conductivity are given in Table 3. The F-value of the model is 432.7078, and the P < 0.0001. This P-value proves that the model is significant.

Table 3. ANOVA results for the thermal conductivity of the nanofluid.

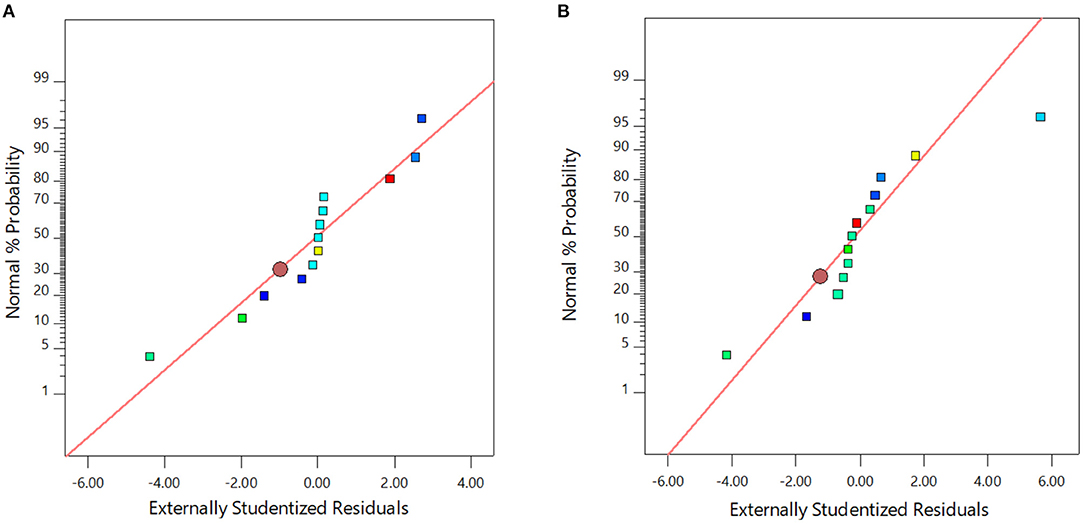
After model development, the next step was to check it with the adequacy test using normal plots for residuals. (1) The model must not follow any pattern or trend and (2) the points must fall close to the straight line. The residual plots for the model of the (a) viscosity and (b) thermal conductivity are shown in Figure 1. It can be observed from Figure 1 that the points do not follow any pattern or trend and are distributed randomly. The result of this test indicates that the model is reliable for prediction. The second validation of the model involves using the outlier plot for both viscosity and thermal conductivity, as shown in Figures 2A,B, respectively. In the outlier plot, the model is not considered reliable if most of the data points fall outside the permissible range. The abnormal data points are those that fall outside the allowable range, which is ±4.5. It can be observed that most of the data points are within the range. Only one point in the thermal conductivity plot is out of the reliable limit, which can be attributed to experimental error (Figure 2).

Figure 1. Normal % probability plots for (A) viscosity and (B) thermal conductivity.

Figure 2. Externally studentized residual plots for (A) viscosity and (B) thermal conductivity.

The last step involved in the model validation was using experimental data for verification. The comparison between predicted and experimental values for both viscosity and thermal conductivity is given in Figure 3. A statistical technique (R²) was used to calculate the error. It was found that the R² for viscosity was 0.9975, while thermal conductivity exhibited an R² of 0.9971.

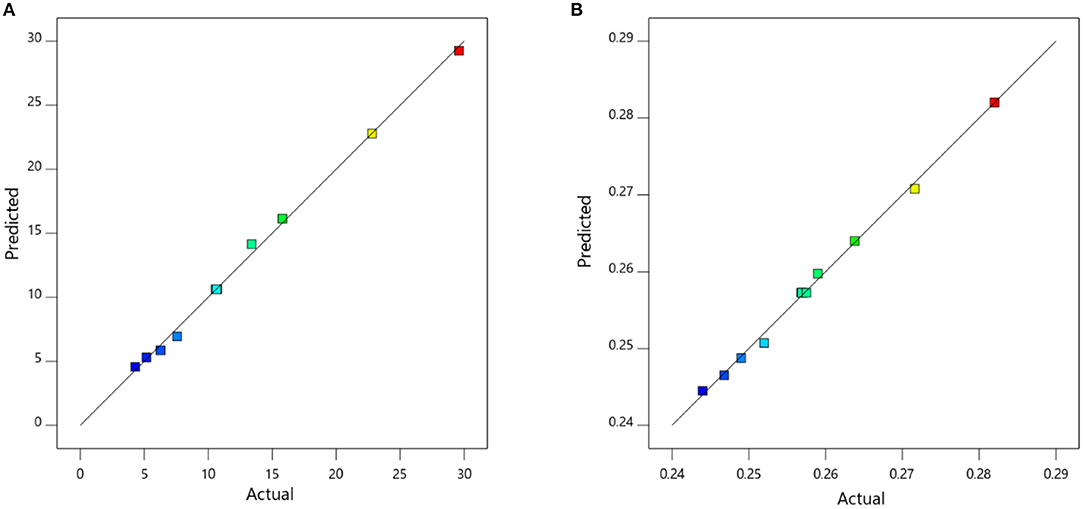
Figure 3. Validation of models using actual (experimental data) for (A) viscosity and (B) thermal conductivity.

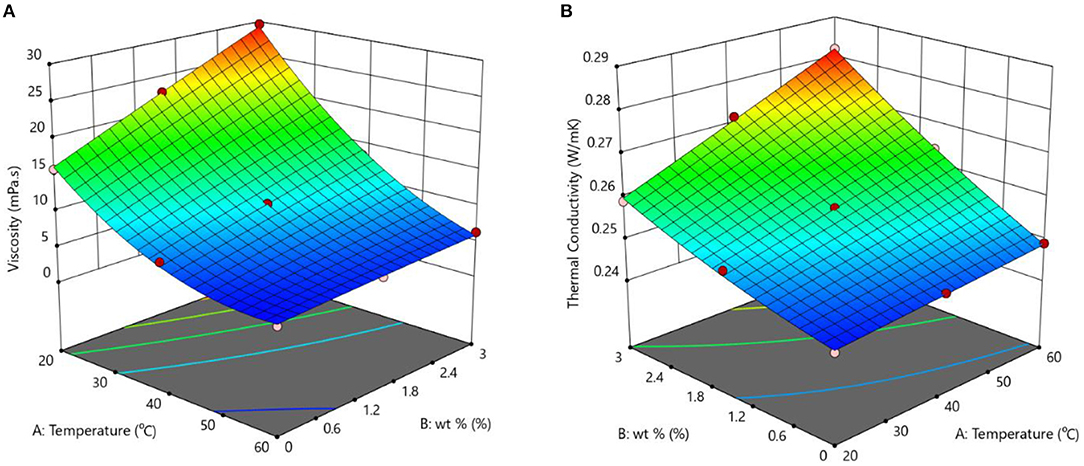
The effect of the process variables (temperature and wt.%) on the response variables (viscosity and thermal conductivity) can be best understood using the 3D plot shown in Figure 4. These plots for viscosity and thermal conductivity of nanodiamond–Ni hybrid nanofluids and are shown in Figures 4A,B, respectively. It can be observed from results that the viscosity significantly increases with an increase in wt.%. It is also observed that the viscosity also increases with the temperature, but this increase is not as significant as that with wt.%. The highest weight percentage (3%) of nanodiamond–Ni nanoparticles dispersion in EG nanofluid showed maximum thermal conductivity improvement, respectively. However, the viscosity enhancement was 1.5-fold for the same weight percentage for ethylene glycol-based nanofluids.

Figure 4. 3D plot for (A) viscosity and (B) thermal conductivity.

Optimization of Process Parameters

The present study included the optimization of two process parameters, namely thermal conductivity and viscosity. The process variables were temperature and wt.%. The developed models were used to generate the data and were further optimized. As it is a multi-objective optimization, the individual and combined effects of the process variables were observed, and a global optimum was calculated for both the thermal conductivity and viscosity. The objective function was set such that the thermal conductivity is maximized while the viscosity is minimized. This specific setting was set for the synthesis of the nanofluid for heat transfer application. The viscosity minimization is helpful in lowering the transportation energy. The optimization goals, limits, and weights are given in Table 4.

Table 4. Optimization cases, objectives, limits, and weights.

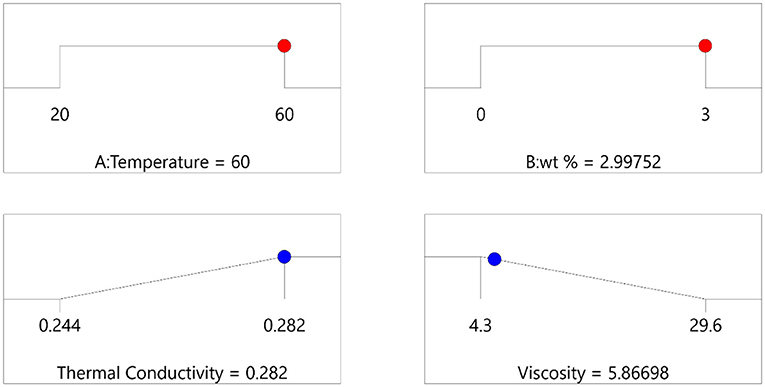
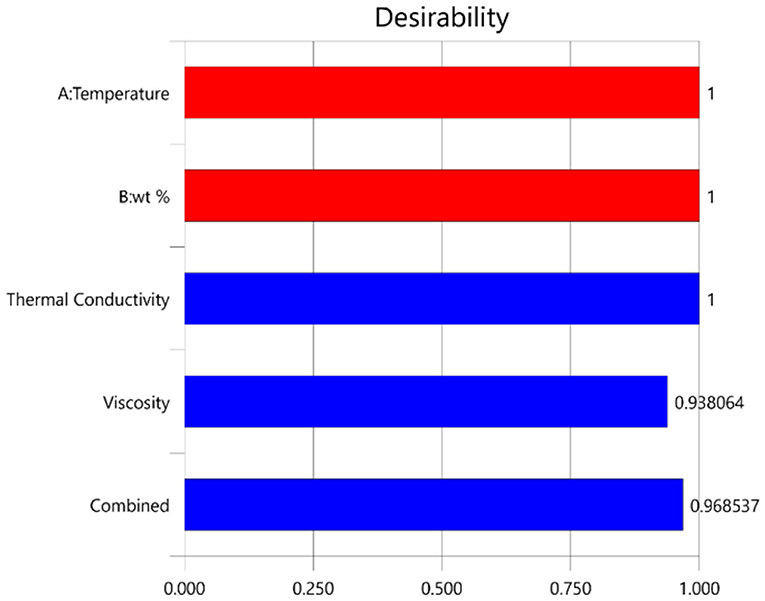
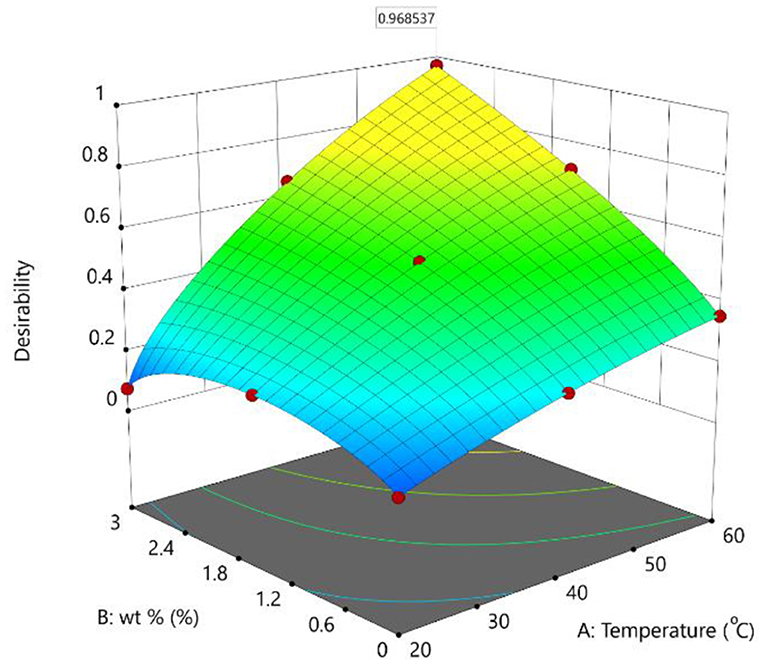
Multiple solutions for the optimization are given in Table 5 and Figure 5. The number 1 solution was selected to be the best solution due to the higher desirability (0.969) and because it is the most suitable for the objective function and goals. The optimum value for thermal conductivity and viscosity were calculated to be 0.282 W/m°C and 5.867 mPa·S, respectively. The corresponding values for temperature and wt.% were 60°C and 2.998%, respectively.

Table 5. Multiple optimization solutions.

Figure 5. Ramp function the optimized solution.

The bar graph and the 3D surface plot between the temperature, wt %, and desirability plot for the optimum solution of the multi-objective optimization are given in Figures 6, 7, respectively. The results showed that a higher desirability of 0.968 was achieved for the optimization solution.

Figure 6. Bar graph for the optimum solution.

Figure 7. 3D surface plot of temperature, wt.%, and desirability.

The desirability plot and the ramp function details were used to ensure the prediction ability for the viscosity and thermal conductivity of nanodiamond–Ni hybrid nanofluids. Similar adequacy tests were also suggested in the reported literature (Danish et al., 2020; Peng et al., 2020). It was evidenced from Table 3 that the overall difference between the experimental dataset and model predictions was negligible, which affirmed the suitability of the applied RSM architecture at operating temperatures and weight percentages.

The outcomes of this investigation exhibit that multi-objective optimization via RSM is an effective technique to determine a feasible solution for thermophysical properties. The optimized temperature and the weight concentration are crucial for the design and operation of heat transfer equipment. However, the investigation can be further extended to a broad range of datasets, and multi-parameter inputs or outputs can be considered in future studies. This may give a more precise optimum solution and an insightful outcome for real applications involving thermal management. The author intends to further expand this research with multi-objective functions including multiple nanofluid properties focusing on the based on the application of heat transfer. It will also include the effect of other properties such as density and specific heat on modeling and optimization.

Conclusions

An RSM–based technique was used for the multi-objective optimization of the thermal conductivity and viscosity of hybrid nanodiamond–Ni-based nanofluids. The effect of the process variables, namely temperature and wt.%, was investigated. Two models were developed for thermal conductivity and viscosity and they were validated with experimental data. The model showed promising results, as the R²-value for thermal conductivity was 0.9971 while it was 0.9975 for viscosity. The optimum value for thermal conductivity and viscosity were computed to be 0.282 Wm/°C and 5.867 mPa·s, respectively. The corresponding values for the temperature and wt.% were 60°C and 2.998%, respectively. It was concluded that the applied methodology can be an effective technique to model and optimize multi-objective parameters for hybrid nanodiamond–Ni-based nanofluids. It is recommended to include more objective functions and parameters involved in nanofluid technology as a future step to get a more practical optimum solution.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author's Note

The author investigated the effect of temperature and concentration on both thermal conductivity and viscosity simultaneously using Response Surface Methodology (RSM). A model for thermal conductivity and viscosity was developed and validated using experimental results. The validated model was further used for the prediction. A detailed multiobjective optimization study was conducted to maximize thermal conductivity and minimize viscosity.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past co-authorship with one of the authors MA.

Acknowledgments

The author would like to gratefully acknowledge the financial and administrative support from the Department of Chemical Engineering and the University of Jeddah Center for Research and Product Development, University of Jeddah, Jeddah, Saudi Arabia.

References