Microstructure-Sensitive Uncertainty Quantification for Crystal Plasticity Finite Element Constitutive Models Using Stochastic Collocation Methods

1 Introduction

Uncertainty quantification (UQ) has been a cornerstone in applied mathematics to verify and validate forward models, with application ranging from subsurface flow, climate change, integrated computational materials engineering (ICME) developments, advanced manufacturing, and many more. In the context of materials design, process-structure-property-performance relationship plays a critical role in establishing the linkage between manufacturing and desired properties, to which materials can be tailored for specific applications. Across the spectrum of length- and time-scales, from quantum to macro-scale, multiple ICME models have been developed in the quest of accurate prediction of materials properties and performance. Notable ICME models for deformation of metals includes, but are not limited to, concurrent or hierarchical couplings of density functional theory, molecular dynamics, kinetic Monte Carlo, dislocation dynamics, crystal plasticity, phase-field, finite element, and any sort of multi-physics and hybrid approaches. Despite its success, there are still much room and open questions for UQ research with respect to microstructure-induced mechanical response in metal alloys.

The concept of ICME models is particularly important because with the predictive capability, engineers can numerically approximate material properties and performance under different operating conditions, without actually performing physical experiments. With the rise of high-performance parallel computing, this step is often hailed as the third paradigm of science Agrawal and Choudhary (2016), supporting prior empirical and experimental, as well as theoretical research. However, as in any forward computational model that relies on deterministic calculations, there is a necessary need to quantify the uncertainty that is associated with the numerical predictions, in order to sufficiently enhance its fidelity and robustness. For the case of crystal plasticity finite element method (CPFEM) as an ICME model that bridges microstructure and materials properties and performance, the question of uncertainty is even more relevant because microstructures are well known to be stochastic, high-dimensional in image or volume representations, and may be anisotropic and heterogeneous.

Numerous UQ studies in computational solid mechanics have been conducted over the last decade. Given the critical importance of optimization and UQ for a wide variety of problems in materials science, several frameworks have been developed, see e.g., Panchal et al. (2013); McDowell (2007); Kalidindi et al. (2016), to provide robust predictions under uncertainty. A comprehensive review of UQ applications in ICME-based simulations can be found in Honarmandi and Arróyave Honarmandi and Arróyave (2020). For example, Zhao et al. Zhao et al. (2022) incorporated measurement and parametric uncertainty to quantify the uncertainty of critical resolved share stress for hcp Ti alloys from nano-indentation. Lim et al. Lim et al. (2019) investigated the mesh sensitivity and polycrystalline representative volume element (RVE), where initial textures, hardening models, and boundary conditions are uncertain, and showed that an adequate polycrystalline RVE is obtained by capturing 1,000 or more grains. Tran and Wildey Tran and Wildey (2020) applied data-consistent inversion method to infer a distribution of microstructure features from a distribution of yield stress, where the push-forward density map via a heteroscedastic Gaussian process approximation is consistent with a target yield stress density. Kotha et al. Kotha et al. (2019a,b, 2020b,a) developed uncertainty-quantified parametrically homogenized constitutive models to capture uncertainty in microstructure-dependent stress-strain curve, as well as stochastic yield surface, which has been broadly applied for modeling multi-scale fatigue crack nucleation in Ti alloys Ozturk et al. (2019b,a) and for single-crystal Ni-based superalloys with support vector regression as an underlying machine learning model Weber et al. (2020). Sedighiani et al. Sedighiani et al. (2020, 2022) applied genetic algorithm and polynomial approximation to various constitutive models, including phenomenological and dislocation-density-based models. Tran et al. Tran A. V. et al. (2019) applied stochastic collocation (SC) method to quantify uncertainty for dendrite morphology and growth via phase-field model. Acar et al. (2017) proposed a linear programming approach to maximize a mean of materials properties under the assumption of Gaussian distribution for both inputs and outputs. Fernandez-Zelaia et al. (2018) utilized Bayesian inference to quantify the uncertainty in stress-strain curves, where model parameters are treated as random variables. Tallman et al. (2019, 2020) applied Gaussian process regression and the Materials Knowledge System framework to predict a set of homogenized materials properties with uncertainty from a distribution function for crystallography orientations and textures. Inductive design exploration method (IDEM) Ellis and McDowell (2017); McDowell et al. (2009); Choi et al. (2008) has been introduced as a materials design methodology to identify feasible and robust design for microstructure features, which has been broadly applied to many practical problems. From a methodological perspective, numerous applied mathematical UQ techniques have been developed over a few decades. While both intrusive and non-intrusive options are available, non-intrusive polynomial chaos expansion (PCE) Xiu and Karniadakis (2002); Najm (2009), which is also known as non-intrusive spectral projection PCE, is one of the most widely used UQ methods to propagate uncertainty in physical models and computational simulations. Global sensitivity analysis methods, which is arguably constructed on top of the high-dimensional model representation, have also well studied. And apparently, numerous studies connecting PCE and global sensitivity analysis, for example, Sudret (2008), Crestaux et al. (2009), and Saltelli et al. (2010), have been conducted. Despite the fact that numerous UQ application works have been carried out in the materials literature and more specifically, in the structure-property relationship, to the knowledge of the authors, none has been applied to quantify the uncertainty related to the underlying constitutive models used in CPFEM.

In this work, we adopt crystallographic textures from Kocks et al. (1998)(cf. Table 1, Chapter 5, pg 185) and Wenk and Van Houtte (2004)(Tables 1 and 2), Raabe et al. (2002), Raabe and Roters (2004), Pham et al. (2017), and Mangal and Holm (2018). We limit the scope of UQ on the microstructure-mechanical property linkage, where the crystal plasticity finite element is widely regarded as the microstructure-aware multi-scale ICME model, and adopt the DREAM.3D Groeber and Jackson (2014) and DAMASK Roters et al. (2019) workflow as previously demonstrated by Diehl et al. (2017), as well as two constitutive models described in Sedighiani et al. (2020, 2022), to perform uncertainty quantification via DAKOTA Eldred (2009); Dalbey et al. (2021).

The rest of the paper is organized as follows. Section 2 introduces PCE and SC as the UQ backbone methodology used in this paper. Section 3 describes the integrated UQ workflow and how they are implemented in practice. Section 4 shows the first case study of 5d UQ for fcc Cu using phenomenological constitutive model with slipping. Section 5 shows the second case study of 16d UQ for hcp Mg using phenomenological constitutive model with slipping and twinning. Section 6 shows the last case study of 7d UQ for bcc W using dislocation-density-based constitutive model. Section 7 discusses and Section 8 concludes the paper, respectively.

2 Uncertainty Quantification Background

In this section, we describe UQ background for CPFEM. In Section 2.1, we summarize the theoretical foundation for generalized polynomial chaos expansion as a non-intrusive spectral projection method. In Section 2.2, we provide the mathematical background for Smolyak sparse grid construction for high-dimensional interpolation and integration, as well as some comparison to full tensor grid highlighting the computational advantage in SC method. We refer interested readers to Babuška et al. (2007); Nobile et al. (2008); Xiu (2009) for a more rigorous mathematical characterization of the SC method.

2.1 Generalized Polynomial Chaos Expansion

The generalized Wiener-Askey PCE Xiu and Karniadakis (2002) represents the second-order random process f(θ) as

where $I_n({\xi }_{i_1},\dots ,{\xi }_{i_n})$ denotes the Wiener-Askey polynomial chaos of order n in terms of the random vector $\mathit{\xi }=({\xi }_{i_1},{\xi }_{i_2},\dots ,{\xi }_{i_n})$, and c’s are polynomial chaos expansion coefficients to be determined. Without loss of generality, Eq. 1 can be rewritten as

where there is a one-to-one correspondence between the function $I_n({\xi }_{i_1},\dots ,{\xi }_{i_n})$ and Φ_j(ξ). Φ_j (ξ(θ)) are orthogonal polynomials in terms of $\mathit{\xi }≔{\{{\xi }_i(\theta )\}}_{i=1}^d$, i.e.,

where δ_ij is the Kronecker delta and ⟨⋅, ⋅⟩ denotes the weighted-average, which is defined as the inner product in the Hilbert space of the variable ξ with respect to the weighting function W(ξ), described in Table 1, as

Here, ${\widehat{f}}_j$ are the coefficients to be determined. In practice, the number of terms in (2) are truncated after a finite term P, where $P+1=\frac{(p+n)!}{p!n!}$, where p is the order of PCE, and n is the dimensionality of the problem, resulting in an approximation for finite PCE, as

The PCE coefficients ${\widehat{f}}_j$ is determined by non-intrusive spectral projection of (5) onto the orthogonal polynomial basis {Φ_j} as

TABLE 1. Relationship between the types of Wiener-Askey polynomial chaos and their underlying random variables θ.

Table 1 describes the relationship between the types of Wiener-Askey polynomial chaos and their corresponding underlying random variables. For uniformly distributed variables ξ used in this paper, the Wiener-Askey scheme Xiu and Karniadakis (2002) requires Legendre polynomials as the polynomial basis {Φ_j}.

2.2 Stochastic Collocation

Sparse grid methods Novak and Ritter (1996, 1997, 1999); Barthelmann et al. (2000) are a cornerstone in high-dimensional interpolation and integration that have been used in a variety of disciplines. In concert with the generalized polynomial chaos expansion Xiu and Karniadakis (2002) as a non-intrusive spectral projection approach, SC methods Babuška et al. (2007); Nobile et al. (2008); Xiu (2009) are developed to improve the efficiency of the generalized polynomial chaos expansion on high-dimensional problems using Smolyak sparse grids for integration. In the nutshell, the polynomial chaos expansion coefficients are computed based on the sparse grid framework that significantly reduces the effect of the curse-of-dimensionality.

Following Nobile et al. (2008), let i ≥ 1 and $\left\{{\xi }_1^i,\dots ,{\xi }_{m_i}^i\right\}\subset [-\mathrm{1,1}]$ be a sequence of abscissas, we begin by introducing the one-dimensional Lagrange interpolation operator as

where $L_j^i(\xi )$ are the Lagrange polynomials of degree m_i − 1, i.e. $L_j^i(\xi )=\prod _{k=1,k\ne j}^{m_i}\frac{(\xi -x_k^i)}{({\xi }_j^i-{\xi }_k^i)}$. The full tensor product formula is perhaps the most straightforward, as

which requires $\prod _{i=1}^n{m}_i$ functions evaluations. Although simple, a major drawback of full tensor product is that the total number of points grows very fast in high dimensions. Numerous choices of collocation points are possible, such as Gauss-Legendre, Clenshaw-Curtis, Leja, and Gauss-Patterson Nobile et al. (2016). In this work, the weakly-nested Gaussian abscissas (see Section 3.6.2 of Dalbey et al. (2021) and Eldred and Burkardt (2009)), which are zeros of orthogonal polynomials, are utilized for quadrature.

Let ${\mathcal{U}}^0=0$ and for i ≥ 1, define

the isotropic Smolyak quadrature formula Smolyak (1963) is given by

or equivalently as,

where q ≥ n is an integer denoting the level of the construction Wasilkowski and Woźniakowski (1995). To compute the operator $\mathcal{A}(q,n)$, one needs to evaluate f on the set of points

where ${\mathit{\xi }}^i=\{{\xi }_1^i,\dots ,{\xi }_{m_i}^i\}\subset [-\mathrm{1,1}]$ is the collection of abscissas used by the univariate interpolating operator ${\mathcal{U}}^i$. This set is a much smaller subset of those required by the full tensor product rule. If the sets are nested, i.e. ξⁱ ⊂ ξⁱ⁺¹, then $\mathcal{H}(q,n)\subset \mathcal{H}(q+1,n)$.

To illustrate the benefits in using the Smolyak sparse grid, compared to the full tensor grid, Table 2 compares the number of simulations required to achieve the same level of accuracy. The dimensionalities are chosen according to the case studies in this paper. The equivalent number points on full tensor grid point is computed as ${(2^{(\ell +1)}-1)}^n$, where ℓ is the corresponding level of sparse grid.

TABLE 2. The number of collocation points used by sparse grid and full tensor grid.

2.3 Variance-Based Global Sensitivity Analysis

Following Sudret (2008), Crestaux et al. (2009), and Saltelli et al. (2010), we summarize the variance-based global sensitivity analysis based on Sobol’ decomposition as follows. In the spirit of generalized polynomial chaos expansion (i.e. Eq. 1 after finite truncation), the Sobol’ decomposition of f(ξ) into the summands of increasing dimensions as

Given a model of the form y = f (ξ₁, ξ₂, … , ξ_n), with y as a scalar, a variance-based first order effect for a generic factor ξ_i can be written as ${\mathbb{V}}_{{\xi }_i}\left[{\mathbb{E}}_{{\mathit{\xi }}_{\sim i}}\left[y|{\xi }_i\right]\right]$, where ξ_∼i is the vector ξ without the i-th element, i.e. ξ_∼i = (ξ₁, … , ξ_i−1, ξ_i+1, … , ξ_n). The main effect sensitivity index (first-order sensitivity coefficient) is written as

It is relatively well-known that

and therefore, the total effect sensitivity index can be obtained as

In global SA, the importance of parameter ξ_i is measured by comparing its variance of the conditional expectation ${\mathbb{V}}_{{\xi }_i}\left[{\mathbb{E}}_{{\mathit{\xi }}_{\sim i}}\left[y|{\xi }_i\right]\right]$ against the total variance $\mathbb{V}[y]$. S_i measures the effect of ξ_i by evaluating the variance contribution of the basis function $\widehat{f_i}$ that depends strictly on the set of variables in ξ_i, while T_i measures the total effect of ξ_i by evaluating the variance contribution of all basis function whose dependencies include ξ_i. For mathematical and implementation details, interested readers are referred to Tang et al. (2010), Weirs et al. (2012), and Crestaux et al. (2009), where most of the computations are based on Monte Carlo sampling ξ. In the context of this manuscript, we can understand ξ as the set of parameters for the underlying constitutive model, whether it is phenomenological or dislocation-density-based, and y as the quantity of interest from the CPFEM model. It should be emphasized that the method used in this study is the mainstream global sensitivity analysis that is widely used in structural reliability studies.

3 Uncertainty Quantification Workflow for Crystal Plasticity

In this paper, we limit the scope of the UQ studies to cases with a unique RVE. As discussed in Section 7, relaxing this restriction will be the subject of future work. DREAM.3D Groeber and Jackson (2014) is used to generate polycrystalline RVE with a specific crystallographic texture, depending on the material considered. DAKOTA Adams et al. (2009) and Python scripts are used to generate inputs for constitutive models, where DAMASK Roters et al. (2019) is employed as the CPFEM forward model. Results are collected and post-processed in DAKOTA.

Figure 1 describes the integrated framework coupling DAKOTA uncertainty quantification code and DREAM.3D + DAMASK workflow. Based on the sparse grid construction specifications, such as anisotropic/isotropic, sparse grid level, as well as other sensitivity analysis options, DAKOTA sets up a list of input parameters to be determined and evaluated by the coupled DREAM.3D + DAMASK workflow. The sets of simulations are then deployed on high-performance computing systems and evaluated in parallel to accelerate the process. Typically, for a fixed input parameter vector, an ensemble of microstructural RVEs are used; however, to reduce the computational cost in this study, we limit the scope of our investigation to one microstructure RVE. It should be noted that, if the initial microstructure is fixed, then DAKOTA would interact directly with DAMASK, and the role of DREAM.3D can be conveniently ignored. Figure 2 shows an isotropic Smolyak sparse grid with Gaussian abscissas in a d=2 problem at various sparse grid level ℓ from 1 to 5, which results in a nested structure that can be exploited to efficient evaluate interpolation or integration in high-dimensional spaces.

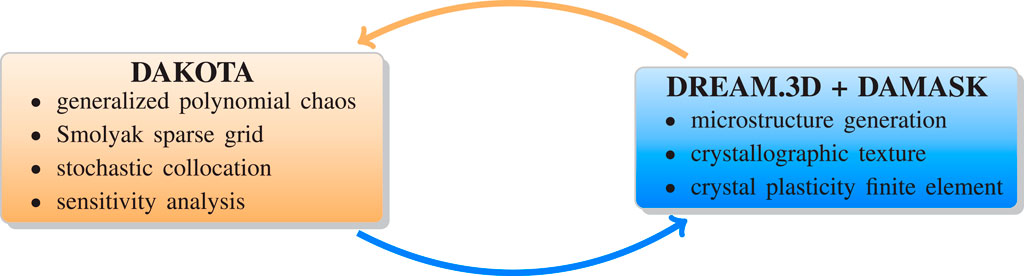
FIGURE 1. Integrating DAKOTA uncertainty quantification workflow to DREAM.3D and DAMASK crystal plasticity finite element simulations. In this framework, DAKOTA queries input parameters to the DREAM.3D + DAMASK automatic workflow, and receives output(s)/quantity (quantities) of interest from DREAM.3D + DAMASK.

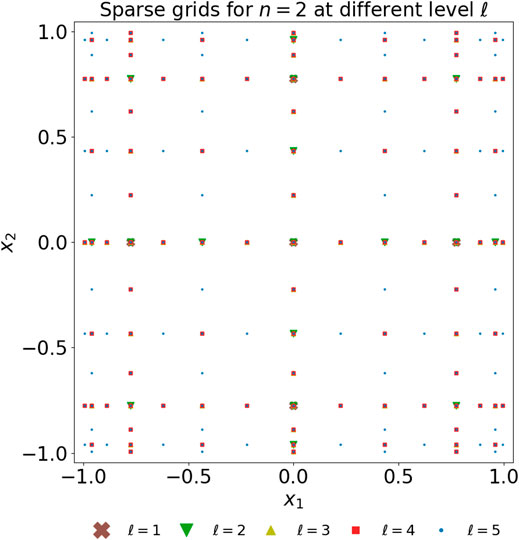
FIGURE 2. Comparison of 2D Smolyak nested sparse grids at various level ℓ, 1 ≤ ℓ ≤ 5, with the number of abscissas varies at 5, 17, 49, 97, 161, respectively, using Gaussian abscissas for quadrature.

In this section, Section 3.1 briefly describes the fundamentals of CPFEM model, whereas Section 3.2 describes the UQ workflow for CPFEM based on DAKOTA UQ package as the wrapper and DREAM.3D and DAMASK as a forward ICME model.

3.1 Crystal Plasticity Model

Consider each point X in the reference configuration being mapped to the current configuration x by a linear transformation with the deformation gradient tensor F, where $\mathbf{F}=\frac{\partial \mathbf{x}}{\partial \mathbf{X}}$. The Lagrangian strain tensor is defined as

The total deformation gradient F can be multiplicatively decomposed into an elastic and plastic parts,

The velocity gradient, which measures the deformation rate, is defined as

where L_p is the plastic velocity gradient evaluated in the intermediate configuration. The second Piola-Kirchoff stress measure S is defined as

where E_e is the elastic Green-Lagrange strain tensor, and $\mathbb{C}$ is the fourth-order stiffness tensor. The plasticity velocity gradient L_p, driven by the second Piola-Kirchoff S, controls the evolution of the plastic deformation gradient as

Constitutive equations representing the flow stress, such as the phenomenological slip-based hardening model and the dislocation density-based hardening model, differ on L_p are calculated based on a specific microstructure and a set of internal state variables. The grain size d in the RVE is a random variable characterized by a log-normal distribution, i.e.,

where μ_D and σ_D are materials-dependent parameters.

3.2 Forward Uncertainty Quantification Problem

In this work, we consider a forward UQ problem for a fixed set (or ensemble) of microstructures using the SC method, where the set of internal state variables for constitutive model parameters are considered stochastic with some inherent uncertainty. While the non-intrusive PCE approach allows an arbitrary probability density of parameters, in this work, uniform distributions are imposed on the constitutive model parameters due to lack of prior knowledge. With the choice of uniform distributions on bounded intervals, according to the Wiener-Askey scheme shown in Table 1, Legendre polynomials are used to approximate the quantities of interest.

In the initial yield regime, we focus on the estimated yield strain ɛ_Y and yield stress σ_Y. From the homogenized stress-strain curve ɛ_vM − σ_vM obtained from a CPFEM simulation, the monotonic cubic interpolation via PCHIP method Fritsch and Butland (1984) is utilized to interpolate ɛ_vM − σ_vM curve. From the approximated stress-strain curve, an estimation of modulus of elasticity is obtained by simple linear regression. An offset at ɛ = 0.002 with the estimated modulus of elasticity is drawn, where the coordinates of the intersection are (ɛ_Y, σ_Y). Statistics of these two quantities of interest are obtained and returned to DAKOTA package.

To set up the UQ study, a pre-processing compilation of constitutive model parameters are obtained from DAKOTA using a numerical toy model. The sets of constitutive model parameters are then appropriately parsed into DAMASK using Python scripts, along with the output of DREAM.3D for setting up the geometric file. With the correct setup of DAMASK simulations, the set of DAMSASK simulations are then performed in a massively parallel manner on a high-performance computing cluster. The post-processing results are then collected from DAMASK, and parsed back to DAKOTA package using a Python interface. DAKOTA then performs the UQ and sensitivity analysis, concluding the UQ workflow for CPFEM based on DREAM.3D and DAMASK.

4 Phenomenological Constitutive Model With Slipping in fcc Cu

4.1 Constitutive Law

We adopt the summary and tabulated parameters from Sedighiani et al. (2020, 2022) (Tables 1, 2). In the phenomenological constitutive model, the shear on each slip system α is modeled as

where τ₀ is the slip resistance, ${\dot{\gamma }}_0$ is the reference shear rate, and n determines the strain rate sensitivity of slip. The influence of other slip system α′ on the hardening behavior of the slip system α is modeled as

where $h_{\alpha {\alpha }^{\prime }}$ is the hardening matrix, which captures the micromechanical interaction among different slip systems

h₀, a, and τ_∞ are slip hardening parameters for all 12 slip systems in fcc materials. $q_{\alpha {\alpha }^{\prime }}$ is a measure for latent hardening with value of 1.0 for coplanar slip system α and α′ and 1.4 otherwise.

4.2 Design of Numerical Experiments

We conducted our analysis with one RVE shown in Figure 3A, where the crystallographic texture is shown in Figure 3B. Average grain size of 60.9467 μm is used, where an RVE of size 256μm³ is generated. A finite element mesh of 16³ is created to approximate the microstructure RVE. In DREAM.3D, the texture crystallography of Copper-type with Euler angles (ϕ₁, θ, ϕ₂) = (90°, 35°, 45°) is used, the grain size parameters are set as μ_D = 4.09, σ_D = 0.2, which results in a RVE with 182 grains, shown in Figure 3A. For DAKOTA, we set the sparse grid level ℓ = 3, dimensionality n = 5, which results in 351 inputs. For each set of input parameters, a CPFEM simulation is performed, followed by the post-process. The results are analyzed in the following section. A uniaxial loading condition is applied in the [100] direction with $\dot{\epsilon }=10^{-3}{\text{s}}^{-1}$.

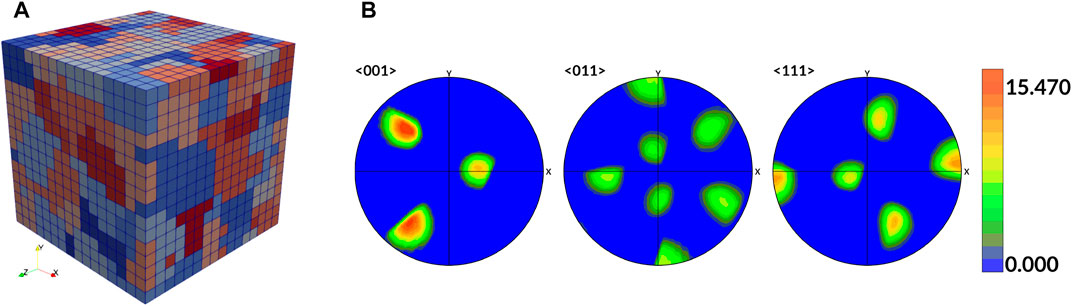
FIGURE 3. (A) Representative volume element for Cu. (B) Copper-type of texture component with Euler angles (ϕ₁, θ, ϕ₂) = (90°, 35°, 45°).

To compare with the default parameter, a single CPFEM simulation is performed with constitutive parameters described in Table 3. The stress-strain equivalent curve is shown in Figure 4. As a reference to experimental data¹, modulus of elasticity for polycrystalline Cu is reported at 110 GPa, whereas its yield strength is reported as 33.3 MPa. Compared to the experiment, the computed modulus and yield strength σ_Y are on the same scale, but off roughly by a factor of 1.5×, possibly due to different processing conditions resulting in slightly different alloys.

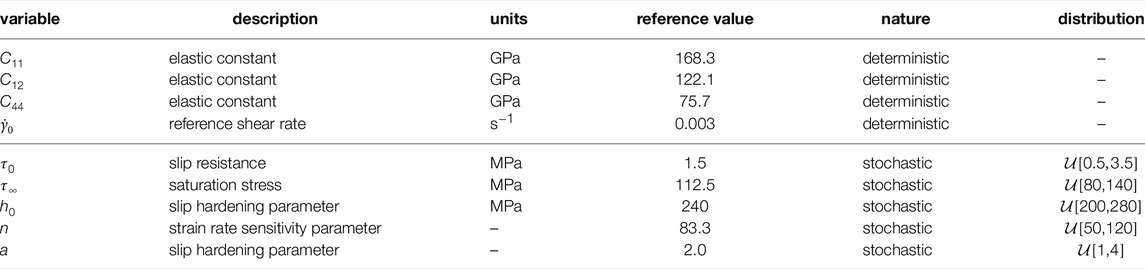
TABLE 3. Parameters for Cu used in this case study [cf. Table 4 Roters et al. (2019) and Tables 1, 2 Sedighiani et al. (2020, 2022)].

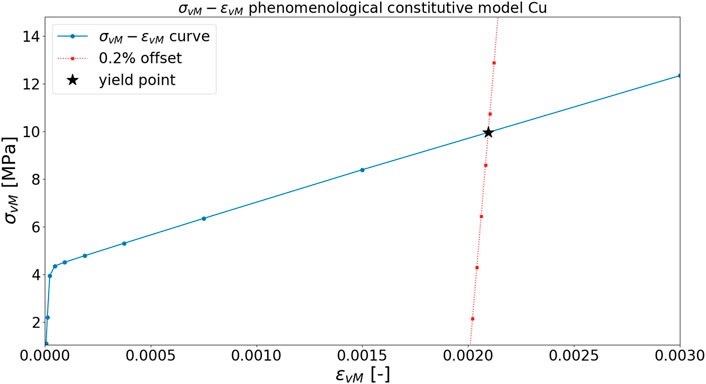
FIGURE 4. Stress-strain equivalent curve for Cu with default parameters and determination of yield point. Modulus of elasticity is estimated as 188.5919 GPa, while (ɛ_Y, σ_Y) are estimated as (0.002052, 9.8527 MPa).

4.3 Numerical Results

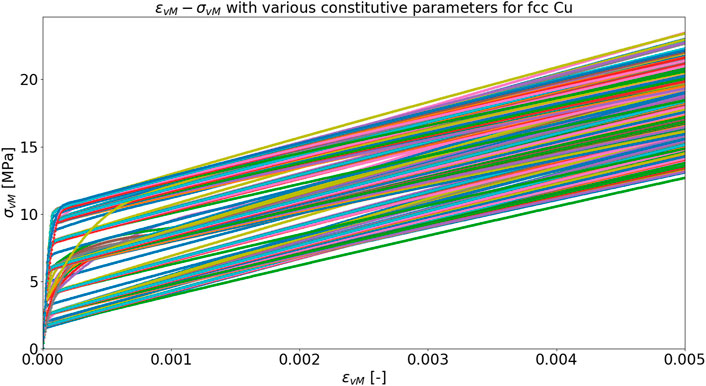
Figure 5 shows a compilation of stress-strain curve for 351 simulations, where each corresponds to a unique set of constitutive parameters for fcc Cu. As shown in this figure, the constitutive model effects not only the initial yield behavior, but also the modulus of elasticity and the hardening behavior.

FIGURE 5. Equivalent ɛ_vM—σ_vM plots for fcc Cu.

Figures 6A,B show the probability density function for ɛ_Y and σ_Y, respectively. The mode for ɛ_Y is approximately 0.00207, whereas the mode for σ_Y is approximately 11.65 MPa. It should be noted that with the current sparse grid level ℓ = 3, the approximation for ɛ_Y may be imprecise. One of the possible reasons is that the elastic regime of copper is very small (as shown in Figure 5), and therefore, a more accurate approximation may be required to accurately capture the yield strain.

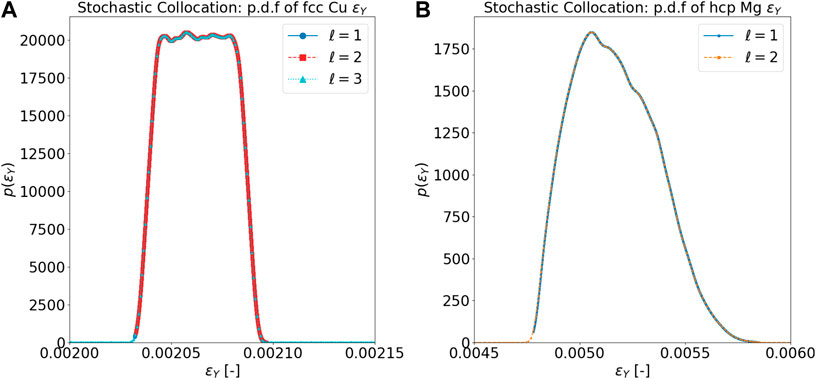
FIGURE 6. (A) SC probability density function of ɛ_Y for fcc Cu. (B) SC probability density function of σ_Y for fcc Cu.

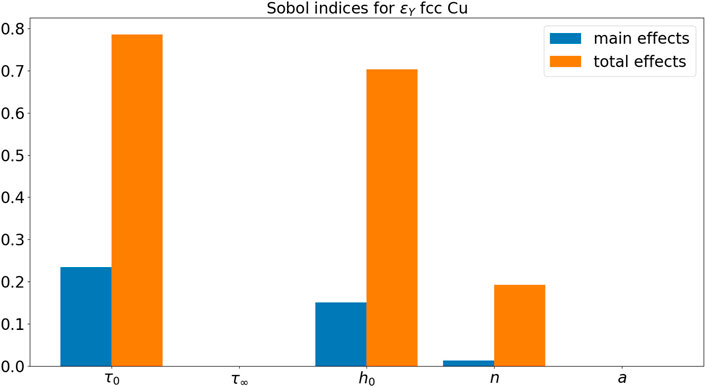
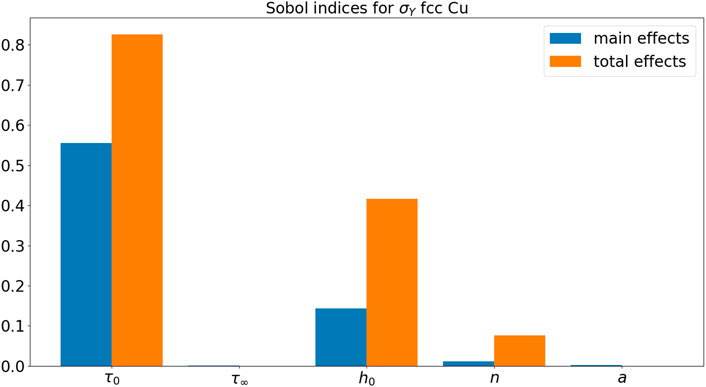
Figure 7 and Figure 8, respectively, show the Sobol’ indices for ɛ_Y and σ_Y. Ranking from the most influential parameters to the least influential parameters for ɛ_Y from the Sobol indices for main effects, $T_{{\tau }_0}=0.7858$, $T_{h_0}=0.7035$, T_n = 0.1922, T_a = −0.01038, and $T_{{\tau }_{\infty }}=-0.001983$. Ranking from the most influential parameters to the least influential parameters for σ_Y from the Sobol indices for main effects, $T_{{\tau }_0}=0.8258$, $T_{h_0}=0.4194$, T_n = 0.07659, T_a = −0.01091, and $T_{{\tau }_{\infty }}=-0.0009990$. The order of influential parameters for fcc Cu, regarding the initial yield behavior, is τ₀ > h₀ > n > a > τ_∞. Since the main scope of this paper is about the initial yield behavior, it is not surprising that Figure 8 agrees with Figure 7 in terms of Sobol’ indices.

FIGURE 7. Sobol’ indices for ɛ_Y for fcc Cu.

FIGURE 8. Sobol’ indices for σ_Y for fcc Cu.

5 Phenomenological Constitutive Models With Dislocation Slip and Deformation Twinning in hcp Mg

5.1 Constitutive Law

Firstly introduced by Hutchinson (1976) and extended for twinning by Kalidindi (1998), the resistance on α = 1, … , N_s slip systems evolve from ξ₀ to a system-dependent saturation value and depend on shear on slip and twin systems according to

where h denotes the components of the slip-slip and slip-twin interaction matrices, $h_0^{\text{s}-\text{s}}$, h_int, c₁, c₂ are model-specific fitting parameters and ξ_∞ represents the saturated resistance evolution.

The resistances on the β = 1, … , N_tw twin systems evolve in a similar way,

where $h_0^{\text{tw}-\text{s}}$, $h_0^{\text{tw}-\text{tw}}$, c₃, and c₄ are model-specific fitting parameters. Shear on each slip system evolves at a rate of

where slip due to mechanical twinning accounting for the unidirectional character of twin formation is computed slightly differently,

where $\mathcal{H}$ is the Heaviside step function. The total twin volume is calculated as

where γ_char is the characteristic shear due to mechanical twinning and depends on the twin system. Interested readers are referred to Section 6.2.2 from Roters et al. (2019).

5.2 Design of Numerical Experiments

Similar to the previous section we restrict the scope to one RVE shown in Figure 9A, where the crystallographic texture is shown in Figure 9B. Average grain size of 204.037 μm is used, where an RVE of size 2048μm³ is generated. A mesh of 64³ is created to approximate the microstructure RVE. In DREAM.3D, the texture crystallography with Euler angles (ϕ₁, θ, ϕ₂) = (90°, 0°, 0°) is used, the grain size parameters are set as μ_D = 5.2983, σ_D = 0.2, which results in a RVE with 1706 grains, shown in Figure 9A. For DAKOTA, we set the sparse grid level ℓ = 2, dimensionality n = 16, which results in 577 inputs. For each set of input parameters, a CPFEM simulation is performed, followed by the post-processing steps. The results are analyzed in the following section. A uniaxial loading condition is applied in the [100] direction with $\dot{\epsilon }=10^{-3}{\text{s}}^{-1}$.

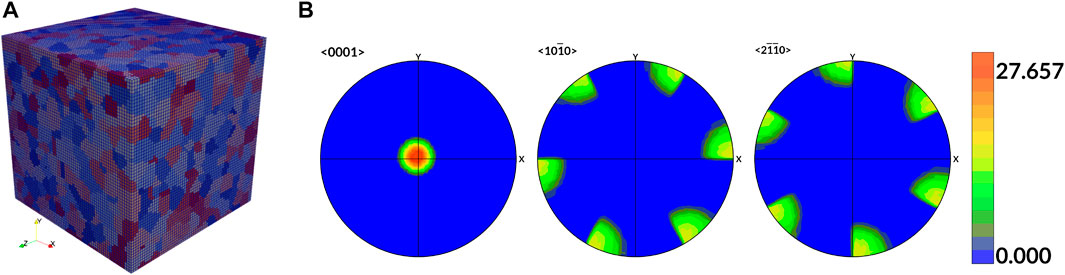
FIGURE 9. (A) Representative volume element for Mg. (B) Magnesium texture component with Euler angles (ϕ₁, θ, ϕ₂) = (90°, 0°, 0°) Mangal and Holm (2018).

To compare with the default parameter, a single CPFEM simulation is performed with constitutive parameters described in Table 4. The stress-strain equivalent curve is shown in Figure 10. As a reference to experimental data², the modulus of elasticity for polycrystalline Mg is reported at 44 GPa, whereas its yield strength is reported as 90–105 MPa. Compared to the experiment, the computed modulus and yield strength σ_Y are well calibrated, as the computational results agree very well with the experimental data.

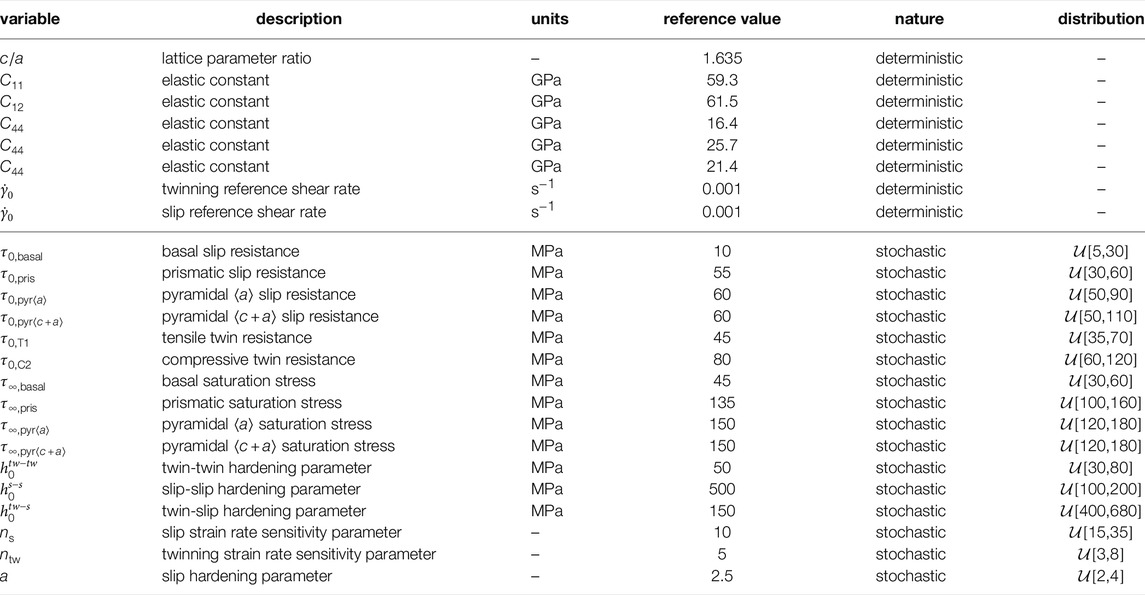
TABLE 4. Parameters for Mg used in this case study (cf. Tables 7 and 8 Sedighiani et al. (2020, 2022), Wang et al. (2014); Tromans (2011); Agnew et al. (2006)).

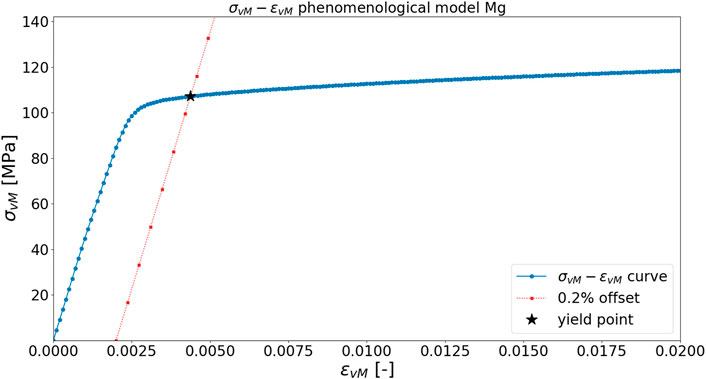
FIGURE 10. Stress-strain equivalent curve for Mg with default parameters and determination of yield point. Modulus of elasticity is estimated as 45.1172 GPa, while (ɛ_Y, σ_Y) are estimated as (0.004375, 107.2 MPa).

5.3 Numerical Results

Figure 11 shows a compilation of stress-strain curves for 577 simulations, where each corresponds to a unique set of constitutive parameters for hcp Mg. As shown in this figure, the constitutive model has a minor effect on the effective modulus of elasticity, and more profound effect on the yield stress σ_Y.

FIGURE 11. Equivalent ɛ_vM—σ_vM plots for hcp Mg.

Figures 12A,B, respectively, show the probability density function for ɛ_Y and σ_Y. The mode for ɛ_Y is approximately 0.0054, whereas the mode for σ_Y is approximately 99 MPa. The uncertainty explained in σ_Y reasonably agree with experimental data.

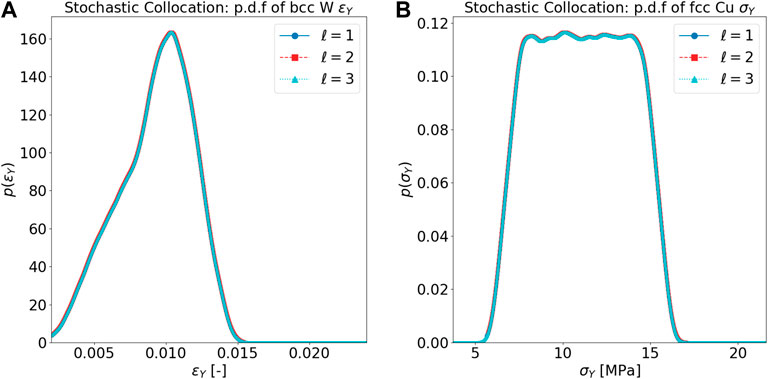
FIGURE 12. (A) SC probability density function of ɛ_Y for hcp Mg. (B) SC probability density function of σ_Y for hcp Mg.

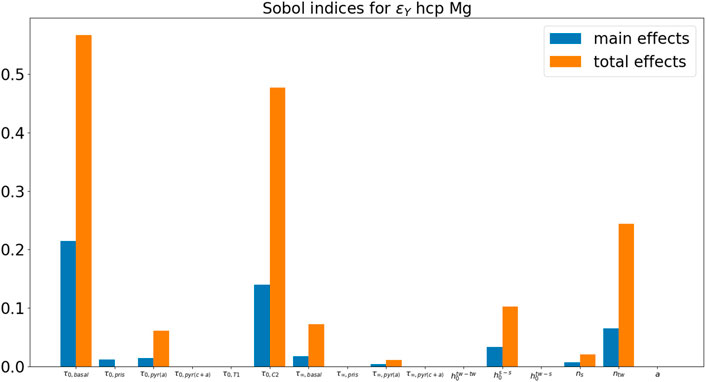
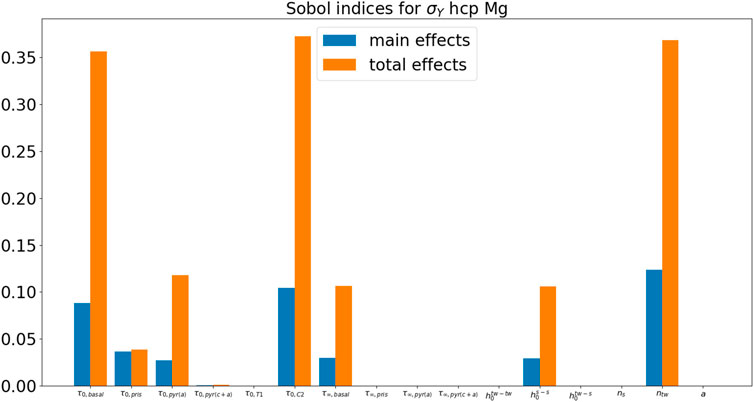
Figure 13 and Figure 14, respectively, show the Sobol’ indices for ɛ_Y and σ_Y. Ranking from the most influential parameters to the least influential parameters for ɛ_Y from the Sobol indices for main effects, $T_{{\tau }_{0,\text{basal}}}=0.5668$, $T_{{\tau }_{0,\text{C}2}}=0.4772$, $T_{n_{\text{tw}}}=0.2439$, $T_{h_0^{\text{s}-\text{s}}}=0.1021$, $T_{{\tau }_{\infty ,\text{basal}}}=0.07249$, $T_{{\tau }_{0,\text{pyr}⟨a⟩}}=0.6131$, $T_{n_{\text{s}}}=0.02082$, $T_{{\tau }_{\infty ,\text{pyr}⟨a⟩}}=0.01091$. Ranking from the most influential parameters to the least influential parameters for σ_Y from the Sobol indices for main effects, $T_{{\tau }_{0,\text{C}2}}=0.3729T_{n_{\text{tw}}}=0.3684$, $T_{{\tau }_{0,\text{basal}}}=0.3566$, $T_{{\tau }_{0,\text{pyr}⟨a⟩}}=0.1181$, $T_{{\tau }_{\infty ,\text{basal}}}=0.1064$, $T_{h_0^{\text{s}-\text{s}}}=0.1061$, $T_{{\tau }_{0,\text{pris}}}=0.03861$. Compared to Sedighiani et al. (2020, 2022), our analysis shows some agreements, but mostly differ in the set of sensitive parameters. Possible explanations are due to (1) different quantities of interest and (2) methodological approach: Sedighiani et al. (2020, 2022) studies are conducted based on ANOVA, whereas our approach relies on global sensitivity analysis with Sobol’ indices.

FIGURE 13. Sobol’ indices for ɛ_Y for hcp Mg.

FIGURE 14. Sobol’ indices for σ_Y for hcp Mg.

6 Dislocation-Density-Based Constitutive Model for bcc W

6.1 Constitutive Law

For the sake of completeness, we adopt the dislocation-density-based constitutive law description from Cereceda et al. (2016, 2015), Stukowski et al. (2015), and summarize it here. Interested readers are further referred to Cereceda et al. (2016, 2015, 2013), Stukowski et al. (2015), especially Cereceda et al. (2016) for a complete formulation.

It is assumed that all the plastic deformation is due to dislocation slip, i.e.

where α is a slip system, m^α and n^α are unit vectors in the normalized slip direction and the normal to the slip plane of the system α, respectively, ${\mathbf{P}}_{\text{S}}^{\alpha }={\mathbf{m}}^{\alpha }\otimes {\mathbf{n}}^{\alpha }$ is a Schmid geometric projection tensor. The resolved shear stress of slip system α include both Schmid and non-Schmid factors as

where ${\mathbf{P}}_{\text{T/AT}}^{\alpha }=a_1{\mathbf{m}}^{\alpha }\otimes {\mathbf{n}}_1^{\alpha }$ is a non-Schmid tensor representing twinning and anti-twinning asymmetry and the effects due to non-glide stress components, ${\mathbf{P}}_{\text{ng}}^{\alpha }=a_2({\mathbf{n}}^{\alpha }\otimes {\mathbf{m}}^{\alpha })\otimes {\mathbb{n}}^{\alpha }+a_3({\mathbf{n}}_1^{\alpha }\otimes {\mathbf{m}}^{\alpha })\otimes {\mathbf{n}}_1^{\alpha }$. ${\mathbf{n}}_1^{\alpha }$ forms an angle of −60° with the reference slip plane defined by n^α and changes sign with the direction of slip on each glide plane Koester et al. (2012). a₁, a₂, a₃ are calibrated material-dependent constants. The shear rate ${\dot{\gamma }}^{\alpha }$ is given by the Orowan equation

where $b=a_0\sqrt{3}/2$ is the magnitude of the Burgers vector, a₀ is the lattice parameter, T is the absolute temperature, ρ^α is the density of mobile screw dislocations in slip system α, and v_s (τ^α, T) is the screw dislocation velocity, which captures the thermally activated character of dislocation motion.

Under the assumption that kink relaxation is significantly faster than kink-pair nucleation, the total time t_t required for a kink pair to form and sweep a rectilinear screw dislocation segment of length λ^α is

where t_n is the mean time to nucleate a kink pair, t_k is the time needed for a kink to sweep half a segment length, J is the kink-pair nucleation rate, w is the kink-pair separation, v_k is the kink velocity.

The kink-pair nucleation rate is modeled by an Arrhenius formulation as

where v₀ is an attempt frequency, ΔH_kp is the activation enthalpy of a kink pair stress τ^α, k is Boltzmann’s constant. The kink velocity is modeled as

where B is simplified to a constant. The dislocation velocity can be modeled as

where $h=a_0\sqrt{6}/3$ is the distance between two consecutive Peierls valleys. When t_k ≪ t_n, $v_{0}B{({\lambda }^{\alpha }-w)}^2\exp \left(-\frac{\mathrm{\Delta }{H}_{\text{kp}}}{kT}\right)\to 0$, and the common diffusive velocity expression is recovered

It is further elaborated in Sedighiani et al. (2020) that

where p and q determine the shape of the short-range activation energy.

Following the Kocks-Mecking family of dislocation density evolution models Mecking and Kocks (1981), the mobile dislocation density on slip system α evolves in time is modeled as

with the initial dislocation density ${\rho }^{\alpha }(t=0)={\rho }_0^{\alpha }$. Dislocation multiplication is proportional to the inverse mean free path of the dislocation λ^α and the plastic strain rate, as

λ^α is defined as

where d_g is the grain size, c is a hardening constant, ${\rho }_f^{\alpha }$ is the forest dislocation density and calculated as

Dislocation annihilation occurs spontaneously when dipoles approach within a spacing of d_edge

The resolved shear stress τ^α is corrected by replacing with ${\tau }^{{\alpha }^{\prime }}$ and accounting for the latent and self-hardening as

where τ_h is the hardening stress, ${\xi }_{\alpha {\alpha }^{\prime }}$ are the coefficients of the interaction matrix between slip system α and α′, respectively, as six possible independent interactions: self, coplanar, collinear, orthogonal, glissile, and sessile.

6.2 Design of Numerical Experiments

For dislocation-density-based CPFEM simulations, we used an RVE shown in Figure 15A, with the crystallographic texture shown in Figure 15B and Euler angles (ϕ₁, θ, ϕ₂) = (0, 0, 45). Average grain size of 3.0339 μm is used, where an RVE of size 32 μm³ is generated. A mesh of 32³ is created to approximate the microstructure RVE. In DREAM.3D, the texture crystallography with Euler angles (ϕ₁, θ, ϕ₂) = (0°, 0°, 45°) is used, the grain size parameters are set as μ_D = 1.0986, σ_D = 0.15, which results in a RVE with 2089 grains, shown in Figure 15A. For DAKOTA, we set the sparse grid level ℓ = 3, dimensionality n = 17, which results in 799 inputs. For each set of input parameters, a CPFEM simulation is performed, followed by the post-process. The results are analyzed in the following section. A uniaxial loading condition is applied in the [100] direction with $\dot{\epsilon }=10^{-3}{\text{s}}^{-1}$.

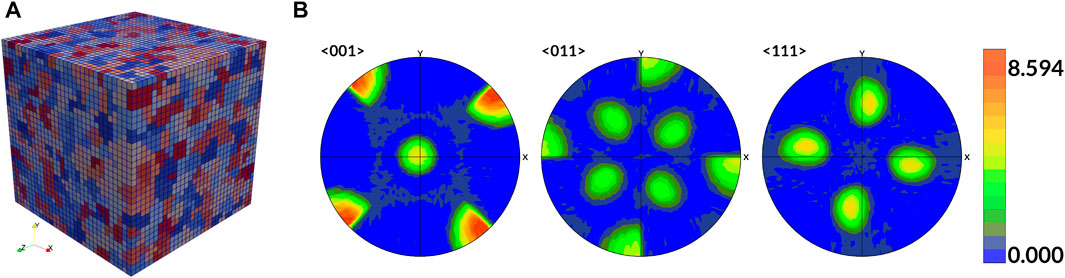
FIGURE 15. (A) Representative volume element for W. (B). Rotated Cube type of texture component with Euler angles (ϕ₁, θ, ϕ₂) = (0°, 0°, 45°).

To compare with the default parameter, a single CPFEM simulation is performed with constitutive parameters described in Table 5. The stress-strain equivalent curve is shown in Figure 16. As a reference to experimental data³, the modulus of elasticity for polycrystalline W is reported at 400 GPa, whereas its yield strength is reported as approximately 750 MPa. Compared to the experiment, the computed modulus agrees very well, but the yield strength σ_Y differs, possibly due to the constitutive model is calibrated for single crystal W, whereas the experimental data is reported for polycrystalline W.

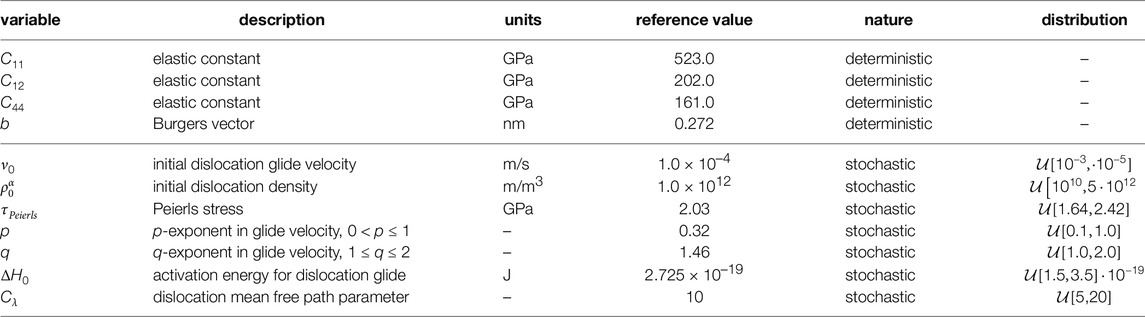
TABLE 5. Parameters for W used in this case study (cf. Tables 2 and 3 in Cereceda et al. Cereceda et al. (2016, 2015), Section 6.2.4 Roters et al. (2019)). Bounds for τ_Peierls are devised based on Samolyuk et al. Samolyuk et al. (2012) and Cereceda et al. Cereceda et al. (2016).

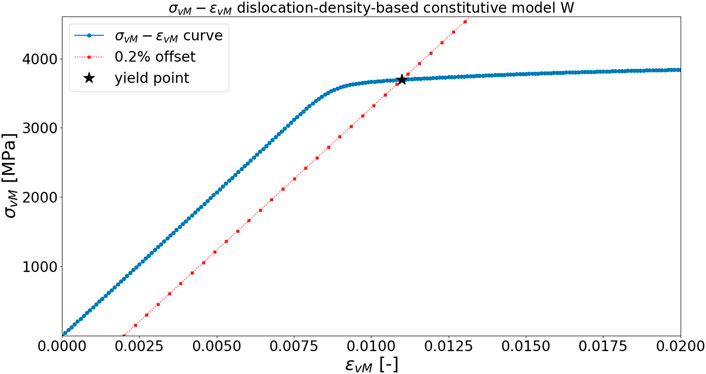
FIGURE 16. Stress-strain equivalent curve for W with default parameters and determination of yield point. Modulus of elasticity is estimated as 411.3528 GPa, while (ɛ_Y, σ_Y) are estimated as (0.01098, 3695 MPa).

6.3 Numerical Results

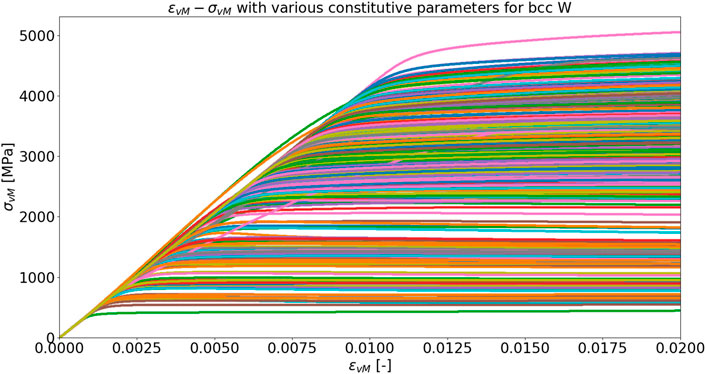
Figure 17 shows a compilation of stress-strain curves for 799 simulations, where each corresponds to a unique set of constitutive parameters for bcc W. As shown in this figure, the constitutive model has a minor effect on the effective modulus of elasticity, and more profound effect on the yield stress σ_Y.

FIGURE 17. Equivalent ɛ_vM − σ_vM plots for bcc W.

Figures 18A,B shows the probability density function for ɛ_Y and σ_Y, respectively. The mode for ɛ_Y is approximately 0.01010, whereas the mode for σ_Y is approximately 3350 MPa. The uncertainty explained in σ_Y reasonably agree with experimental data. For experimental data with σ_Y ≈ 750 MPa, fairly a few set of parameters can reproduce and calibrate accordingly, as shown in Figure 17.

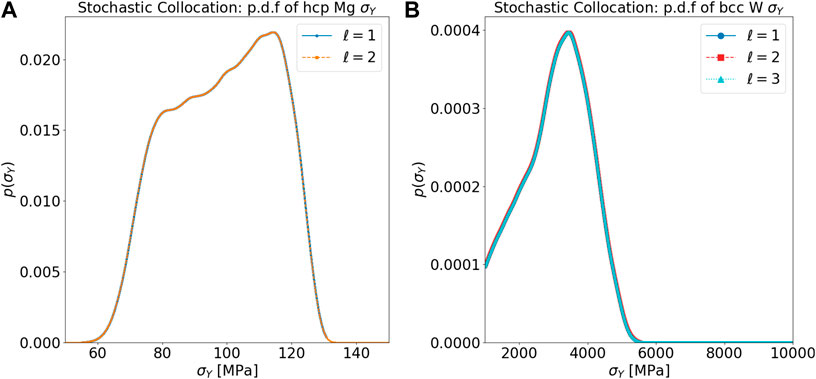
FIGURE 18. (A) SC probability density function of ɛ_Y for bcc W. (B) SC probability density function of σ_Y for bcc W.

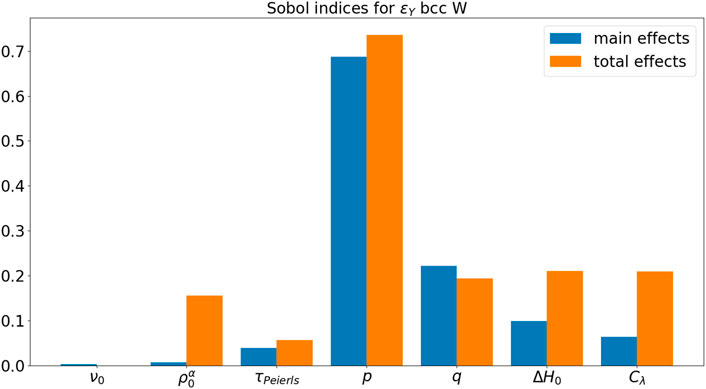
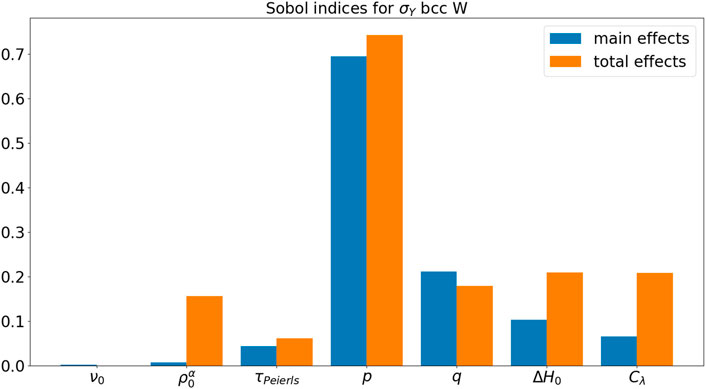
Figure 19 and Figure 20, respectively, show the Sobol’ indices for ɛ_Y and σ_Y. Ranking from the most influential parameters to the least influential parameters for ɛ_Y from the Sobol indices for main effects, T_p = 0.7356, $T_{\mathrm{\Delta }{H}_0}=0.212$, $T_{C_{\lambda }}=0.2089$, T_q = 0.1942, $T_{{\rho }_0^{\alpha }}=0.1556$, $T_{{\tau }_{\text{Peierls}}}=0.05712$, $T_{{\nu }_0}=-0.03444$. Ranking from the most influential parameters to the least influential parameters for σ_Y from the Sobol indices for main effects, T_p = 0.5668, $T_{\mathrm{\Delta }{H}_0}=0.2095$, $T_{C_{\lambda }}=0.2079$, T_q = 0.1795, $T_{{\rho }_0^{\alpha }}=0.1560$, $T_{{\tau }_{\text{Peierls}}}=0.06172$, $T_{{\nu }_0}=-0.03663$. Since the ranking does not change when the quantity of interest changes from ɛ_Y to σ_Y, we conclude that the importance of parameters is $p>\mathrm{\Delta }{H}_0>C_{\lambda }>q>{\rho }_0^{\alpha }>{\tau }_{\text{Peierls}}>{\nu }_0$.

FIGURE 19. Sobol’ indices for ɛ_Y for bcc W.

FIGURE 20. Sobol’ indices for σ_Y for bcc W.

7 Discussion

In this paper, we conducted several UQ studies for constitutive models in CPFEM with a single microstructure RVE for each case study. Three case studies are performed with different crystal structures, namely fcc, hcp, and bcc, for Cu, Mg, and W, respectively. In this paper, three materials systems with different crystal structures (fcc, bcc, and hcp) are studied. Depending on the crystal structure, there may be different slipping and twinning systems in terms of slipping and twinning directions in plastic deformation, leading to interesting materials behaviors and mechanisms. The quantities of interest are selected as the initial yield strain ɛ_Y and the initial yield stress σ_Y. For fcc Cu, parameter τ₀ is the most influential parameter for the initial yield behavior. For hcp Mg, all τ_0,basal, τ_0,C2, and n_tw parameters are influential for the initial yield behavior. For bcc W, p parameter in the short-range activation energy model is the most influential parameter for the initial yield behavior.

UQ studies, such as those described in this manuscript, play an important role in constitutive model calibration for unknown material system in the future. Since there are only a limited number of physical constitutive models, it is important to conduct a UQ study to observe the range of quantities of interest, and to numerically rank the influence of constitutive model parameters. Based on the stress-strain compilation curve conducted for various constitutive model parameters, the material behaviors can be rigorously quantified. The obtained UQ results provide a foundational step for further constitutive model calibration for future works, mostly conducted via digital image correlation techniques Turner et al. (2015); Reu et al. (2018, 2021).

Compared to polynomial approximation with full tensor grid, sparse grid approaches have a significant computational advantages, where this advantage grows with increasing dimensionality thanks to a slower growth rate Nobile et al. (2008). In the context of constitutive models, the computational reduction is mostly profound in the case of hcp system (as opposed to bcc and fcc), such as Mg and Ti, and in the case of dislocation-density-based constitutive model (as opposed to phenomenological model), where many parameters require careful calibration to obtain a sufficient agreement with experiments. For simple system with a relatively simple phenomenological constitutive model, the computational reduction is less severe. It is noteworthy that the level of the Smolyak sparse grid in this study has a little effect on the resulting probability density function of QoIs. This implies that the underlying function is perhaps mostly low-order. This observation can also be confirmed by the Sobol’ indices, where the first-order Sobol’ indices are much more dominant, compared to higher-order Sobol’ indices.

To construct the response surface model, stochastic collocation provides a significant advantage for reducing the curse of dimensionality. However, when it comes to accuracy, Gaussian process regression, which is also the underlying surrogate model for Bayesian optimization, is arguably one of the best approaches in shallow machine learning. The direction of coupling Bayesian optimization, e.g., Tran A. et al. (2019, 2020, 2021); Tran (2019); Tran et al. (2022), for robust constitutive model calibration remains open for future research.

The scope of this manuscript is to quantify the microstructure-sensitive uncertainty. Obviously, it can be expanded to account for the entire stress-strain curve. However, due to the number of parameters involved in each constitutive model, there are hundreds to thousands of runs needed for a single microstructure RVE. Such computationally expensive numerical experiments require careful planning and execution, and therefore, remain a potential topic for future studies. It is important to point out that by restricting to one RVE per case study, this work does not address microstructure-sensitive uncertainty that either is related or induced by the underlying stochastic nature of microstructures. The direction of investigating a microstructure ensemble with many RVEs remain open for future work.

8 Conclusion

In this paper, we applied SC to quantify uncertainty associated with the initial yield behavior, mainly the estimated yield strain ɛ_Y and the estimated yield stress σ_Y for fcc Cu, hcp Mg, and bcc W. A variety of constitutive models are used, resulting with different parameterization and dimensionalities for the constitutive models considered. To mitigate the curse of dimensionality, Smolyak sparse grid is employed for high-dimensional integration to evaluate the PCE coefficients. Variance-based global sensitivity analysis is used to study the sensitivity analysis of the constitutive model parameters.

In light of the computational results presented in previous sections, there are several influential parameters that may have a significant effect on the initial yield behavior. For the phenomenological constitutive model, the slip resistance τ₀, the slip hardening parameter h₀, and the strain rate sensitivity parameter n are the most influential parameters, ranking in descending order. For the dislocation-density-based constitutive model, the p-exponent in glide velocity is the most influential parameter, followed by the activation energy for dislocation glide ΔH₀, the dislocation mean free path parameter C_λ, the q-exponent in glide velocity, and the initial dislocation density ${\rho }_0^{\alpha }$. We conclude that in both constitutive models considered in this study, i.e. phenomenological (with and without twinning) and dislocation-density-based constitutive models, regarding the initial yield behavior, some parameters may have a profound effect on the QoI, while some others may not have a significant effect. The observation could potentially pave way for dimensionality reduction in constitutive model calibration in the future.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

AT conceptualizes, performs simulations, analyzes data, and drafts the manuscript. BT and TW consults in uncertainty quantification aspect. HL consults in crystal plasticity finite element aspect.

Author Disclaimer

The views expressed in the article do not necessarily represent the views of the United States Department of Energy or the United States Government. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the United States Department of Energy’s National Nuclear Security Administration under contract DE-NA-0003525.

Conflict of Interest

Authors AT, TW, HL are employed by the company Sandia National Laboratories Giorgia.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹https://www.matweb.com/search/DataSheet.aspx?MatGUID=9aebe83845c04c1db5126fada6f76f7e.

²https://www.matweb.com/search/DataSheet.aspx?MatGUID=7b49605d472d40d393ffe87ea224980c.

³http://www.matweb.com/search/DataSheet.aspx?MatGUID=41e0851d2f3c417ba69ea0188fa570e3.

References