Performance analysis of the functionally graded flexoelectric-piezoelectric energy harvesting
- 1Fujian Provincial Key Laboratory of Advanced Materials, College of Materials, Xiamen University, Xiamen, China
- 2Xiamen Key Laboratory of Electronic Ceramic Materials and Devices, College of Materials, Xiamen University, Xiamen, China
In the present paper, the output performances of the functionally graded flexoelectric-piezoelectric (FGFP) energy harvesting subjected to an external harmonic excitation, considering the effect of piezoelectric polarization direction, are addressed. Based on the Euler-Bernoulli beam model and generalized Hamiltonian principle, the dynamic governing equations and the corresponding boundary conditions of the functionally graded flexoelectric-piezoelectric energy harvesting are obtained. The natural frequency equation and the closed-form analytical expressions of electromechanical responses are further deduced. The numerical results show that the output performance of the functionally graded flexoelectric-piezoelectric energy harvesting is dependent on the piezoelectric polarization direction, gradient index and structure size. At the nanoscale, the flexoelectric effect dominates the output performances; however, at the microscale, the gradient piezoelectric effect dominates the output performances. At transition scales, from nano to micro, the output performances are very small sometimes, where, in some case, the gradient piezoelectric effect and flexoelectric effect cancel each other. The present study reveals the importance of the piezoelectric polarization direction and gradient index on the output performance of the functionally graded flexoelectric-piezoelectric energy harvesting from nano to micro scales.
Introduction
With the rapid development of nanotechnology, a large number of small electronic devices such as sensors, actuators and wireless transmitters have been integrated into every corner of the world for health monitoring, environmental protection, remote controls and wireless transmission (Hudak and Amatucci, 2008). These devices require only a small amount of electricity, and there is waste energy in the environment where micro-nano devices work. Converting ambient energy into electricity to power micro-nano devices is considered a promising approach, which has the advantages of small size, long life, no pollution and high energy density (Zi and Wang, 2017). In addition, some important system-level and circuit-level works about micro-scale energy harvesting have been reported (Chao et al., 2007; Lu et al., 2011). Piezoelectric and flexoelectric effects are ubiquitous in a wide variety of materials (Ma and Cross, 2001). Piezoelectric effect is described as the asymmetric shift of charges or ions of piezoelectric materials when subjected to mechanical strain (Sezer and Koç, 2021), which only exists in non-centrosymmetric dielectric materials. The flexoelectric effect is defined as the coupling between strain gradients and electrical polarization (Fu and Cross, 2007; Deng, 2017), which exists in all dielectrics and exhibits strong size-dependent properties at the nanoscale (Yan et al., 2013). Therefore, it is necessary to consider the flexoelectric effect in analyzing the electromechanical coupling of dielectrics at the nanoscale. Even in some micro-electromechanical systems or almost all nano-electromechanical systems, flexoelectric materials can replace piezoelectric materials (Zhang et al., 2014).
Recently, a series of studies have been conducted on the electromechanical coupling of nanobeams or nanoplates with flexoelectric effect. Cross (2006) firstly measured the flexoelectric coefficients of ferroelectric, incipient ferroelectric and relaxor ferroelectric perovskites by quasi-static and low frequency dynamic techniques. Majdoub et al. (2008) firstly discussed the electromechanical coupling responses of the nano-beams with strain gradient using molecular dynamics and linear piezoelectric theory. Their results showed that the piezoelectric and flexoelectric effects exhibit a non-linear interaction in piezoelectric materials. Shen and Hu (2010) established a theoretical framework including the electrostatic force, flexoelectricity, and surface effects through the variational principle of dielectrics. Based on the extended linear piezoelectric theory and Timoshenko beam model, Yan and Jiang (2013a), Yan and Jiang (2013b) found that the flexoelectric effect has a significant influence on the static bending and free vibration of simply supported piezoelectric nanobeams, and the flexoelectric effect is also sensitive to the mechanical boundary conditions and the direction of the applied electric field. Liang et al. (2014) investigated the influence of surface effect and flexoelectricity on the buckling and vibration of piezoelectric nanowires based on a continuum framework and the Euler-Bernoulli beam hypothesis. They detected that the effective Young’s modulus and bending rigidity are enhanced by flexoelectricity. Zhang et al. (2014) analyzed the influence of flexoelectric effect on the vibration behavior of piezoelectric nanoplate. Deng et al. (2014) discussed the flexoelectric energy harvester in the nanoscale based on the internal energy density. They solved the electromechanical frequency responses using the assumed-modes method. Wang and Wang (2016) developed an analytical model incorporating flexoelectric effect for nanoscale unimorph piezoelectric energy harvesters. In their analysis, when the thickness of the piezoelectric layer is small, the flexoelectric effect has a great influence on the voltage output and power output. Zhou et al. (2017) investigated the electromechanical coupling response of piezoelectric nanobeams with different electrical boundary conditions, in which the results showed that flexoelectricity effect has significant influence on stiffness and induced electric potential of the nanobeam. Moura and Erturk (2017) applied the distributed-parameter method to discuss the flexoelectric energy harvesters in elastic dielectrics. Zhao et al. (2019) studied the non-linear bending and free vibration of Timoshenko piezoelectric nanobeam incorporating flexoelectricity and surface effect. Their results indicated that strain gradient elastic effect, flexoelectricity, surface effect and applied electric voltage have significant influences on the non-linear mechanical behaviors of nanobeam. Su et al. (2019a) simulated the flexoelectric energy harvesting under the harmonic mechanical excitation. In the work, the closed-form voltage output, power density, and mechanical vibration response were obtained, which exhibit significant scale effects at the nanoscale. The above studies mainly focus on monolayer nanostructures, in which the piezoelectric effect can be ignored (Zhou et al., 2017). However, the micro-nano systems, constructing the bilayer or multilayer structures, always exhibit both piezoelectricity and flexoelectricity. Erturk and Imman (2008) derived the distributed parameter electromechanical model to analyze the unimorph piezoelectric energy harvester based on a uniform composite the Euler-Bernoulli beam. Li et al. (2014a) proposed a size-dependent model of a three-layer microbeam including a flexoelectric dielectric layer. Both the static bending and free vibration problems of cantilever and simply supported microbeams were studied. Abdollahi and Arias (2015) numerically analyzed the interplay between piezoelectricity and flexoelectricity in flexural sensors and actuators. They found that flexoelectricity could reduce or enhance the effective piezoelectric effect and electromechanical coupling, which is dependent on the structure design. Qi et al. (2016) established the bending model of an electro-elastic bilayer nanobeam. Their results demonstrated that both the strain gradient elastic effect and the flexoelectric effect significantly affect the deflection of the nanobeam. Su et al. (2019b) examined the electromechanical response of bilayer piezoelectric sensors due to flexoelectricity and strain gradient elasticity. The flexoelectric effect can significantly enhance the electrical performance of bilayer piezoelectric sensors at the nanoscale. Interestingly, the piezoelectric polarization direction of the piezoelectric layer also affects the electromechanical response of the system. Rojas et al. (2021) studied the output of piezoelectric only, flexoelectric only, and combined electromechanical configurations over various scales. Their results revealed that the combined system outperforms either piezoelectric only or flexoelectric only configuration from nano to micro scales. Fu and Zhang (2022) established a size-dependent bilayer piezoelectric microbeam model considering the strain gradient effect based on the modified piezoelectric theory. Fu and Zhou (2021) suggested a size-dependent model of the laminated microbeam partially covered by the flexoelectric layer, which solved the static bending problem of the beam under uniform load and voltage. All the above studies are static or dynamic electromechanical coupling analysis of mono-layer or multi-layer nanostructures. However, there are some studies on improving the effective flexoelectric effect through structural design or uneven distribution of materials. The introduction of functionally graded materials (FGMs) to improve material properties is a very useful and sensible approach (Ma and Lee, 2012; Ke et al., 2014). Combining flexoelectricity and simple functional grading, Mbarki et al. (2014) quantitatively demonstrated the possibility of achieving apparent piezoelectric materials with large and temperature-stable electromechanical coupling above the Curie temperature. Rafiee et al. (2014) addressed the non-linear analysis of energy harvesting, which is composed of FG piezoelectric carbon nanotube reinforced composite plates, under combined thermal and mechanical loadings. The results showed that temperature variation and material distribution have a great effect on the amplitude of vibration and the average harvested power. Li and Pan (2015) numerically solved the static bending and free vibration problems of FG piezoelectric microplates based on the modified couple-stress theories. Kumar et al. (2018) demonstrated the induced flexoelectricity in dielectric FGMs due to non-uniform Youngs’s modulus along the thickness. Their results showed that the optimum gradient index of FGMs can greatly enhance the output voltage. Chu et al. (2018), Chu et al. (2019) discussed the flexoelectric effect in FG composite piezoelectric nanobeams and FG flexoelectric nanocylinders. The results revealed that the static bending, free vibration behavior and electromechanical properties can be significantly influenced by the given FG configuration with graded material parameters. Furthermore, based on the non-local simplified strain gradient elasticity theory, Chu et al. (2020) analyzed the thermally induced non-linear dynamic behaviors of FG flexoelectric nanobeams, in which the thermally induced bending amplitude and non-linear frequency were discussed. Nan et al. (2020) studied the static bending and free vibration problem of porous FG piezoelectric nanobeams and indicated the gradient index, porosity distribution, external electrical voltage, flexoelectric effect and boundary conditions have significant effects on the static deformation and natural frequency of the nanobeams. Recently, Chen et al. (2021) analyzed the mechanical and electrical properties of FG flexoelectric sensors under different electrical boundary conditions. The results showed that the flexoelectric effect, piezoelectric effect, and gradient distribution have considerable influences on the electromechanical performance of the FG flexoelectric sensors. Moreover, the non-uniform piezoelectricity and piezoelectric polarization direction will play a leading role in the induced electric potential at a large scale. The flexoelectric effect will dominate the induced electric potential at the nano scale. However, it is important to clearly explain the interaction between the piezoelectricity and flexoelectricity in the FGFP energy harvesting. To the best of our knowledge, the effects of piezoelectric polarization direction, flexoelectric-piezoelectric distribution and gradient index on the FGFP energy harvesting have not been studied clearly. The closed-form analytical solutions for the FGFP energy harvesting have not been reported, which will be easy to understand and apply in practice.
The main goal of the present paper is to investigate the influence of piezoelectric effect, flexoelectric effect and gradient index on the FGFP energy harvesting at various scales. A FGFP energy harvesting with a tip mass has been analyzed using the coupled distributed-parameter model. Applying FGMs in the form of exponential distribution, based on electric Gibbs free energy and generalized Hamilton’s variational principle, the natural frequency equation under different electrical conditions and the closed-form analytical expressions of output performances under base excitations are derived. The effects of the piezoelectric polarization direction and gradient index on the performance of FGFP energy harvesting are discussed in detail.
Governing equation and boundary conditions of the FGFP energy harvesting
Figure 1 shows the schematic of the FGFP energy harvesting considered in the present study with length
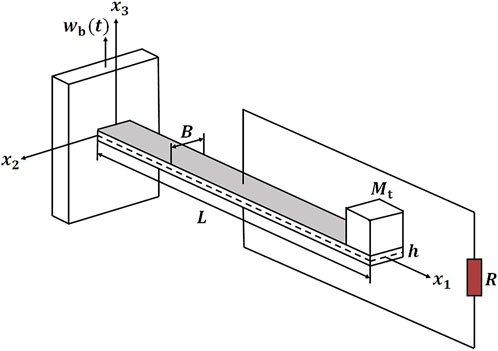
FIGURE 1. A schematic configuration of the FGFP energy harvesting with a tip mass under the base excitation.
It is assumed that the top surface
where the
For the slender beam, combined with the small deformation assumption for Euler-Bernoulli beams, it can be assumed that the mechanical displacement vector
where
where
For the slender beam structure, the strain gradient in the axial direction
Under the assumption of infinitely small deformation, the constitutive equation of the FGFP energy harvesting can be derived as (Zhou et al., 2017; Chen et al., 2021):
where
For simplicity, the dielectric coefficient, piezoelectric coefficient and flexoelectric coefficient of the FGFP energy harvesting have the same gradient distribution, which means
Considering the surface electrical boundary conditions
where
Substituting Eq. 8 into Eq. 6, the stress, higher order stress, and electric displacement of the FGFP energy harvesting can be written as:
For a dielectric material with flexoelectricity and piezoelectricity, a linearized extension of piezoelectric theory has been used. Considering the coupling relationship between the strain gradient and the electric field strength, the electric Gibbs free energy density function
Combining Eqs. 5, 8 and 10, The electric Gibbs free energy density function can be expanded as:
where
The generalized Hamiltonian principle of the FGFP energy harvesting can be expressed as follows (Liang et al., 2015; Su et al., 2019a):
where
where
Using Eqs. 12, 15, the variational expression of total electric Gibbs free energy of the FGFP energy harvesting can be written as (Su et al., 2019a):
where three parameters have been introduced.
Further substituting Eqs. 15, 16 into Eq. 14, the generalized Hamiltonian variational equation of the FGFP energy harvesting can be derived:
where
where
where
Similarly,
When the external load resistor
where
Free vibration responses of the FGFP energy harvesting
Natural frequency of the FGFP energy harvesting under the electrical open circuit condition
In this section, the free vibration of the FGFP energy harvesting under the electrical open circuit condition is investigated. The top and bottom surfaces of the cantilever beam are equipotential bodies because they are covered with electrodes. Hence, the electric potential difference
Correspondingly, Eq. 23 could be rewritten as:
when the FGFP energy harvesting is bending, the surface charge will be redistributed on the electrodes. However, the total charge should remain zero, then Eq. 21 could be simplified to:
And substituting Eq. 26 into the third equation of Eq. 25, the complete mechanical boundary condition can be obtained:
The separated variable method is employed to solve the natural frequency of the FGFP energy harvesting. Considering the form of Eq. 24, its solution can be set as:
where
From the Eq. 30,
where
To ensure that Eq. 32 has the non-zero solution, the corresponding coefficient determinant of Eq. 32 should be equal to zero. The characteristic equation of the natural frequency of the FGFP energy harvesting in the open circuit condition is:
Equation 34 is a transcendental equation about the eigenvalue
Natural frequency of the FGFP energy harvesting under the electrical short circuit condition
For the electrical short circuit condition, the top and bottom surface electrodes of the beam are connected by wires, and the induced potential between the top and bottom surface electrodes is zero. Hence, the governing equation and boundary constraints of free vibration are simplified as:
Similarly, the circular frequency of system vibration in the electrical short circuit condition is
Electromechanical coupling responses of the FGFP energy harvesting
The vibration response of the FGFP energy harvesting can be written as a linear combination of series of vibration modes:
where
where
where
It should be noted that the output electric potential difference
where
It is assumed that the fixed end of the energy harvesting is excited by a translational displacement in the transverse direction. The external excitation is a harmonic form with a circular frequency
where
Numerical results and discussion
Effect of the piezoelectric polarization direction on electromechanical coupling coefficient
To assess the effect of the piezoelectric polarization direction on performance of the FGFP energy harvesting, we simply change the piezoelectric coefficient to positive or negative, which expresses the opposite polarization direction. The piezoelectric coefficient of the FGFP energy harvesting Ⅰ is set to a negative value, and the corresponding top and bottom parameters are
The normalized bending stiffness of the FGFP energy harvesting is defined as
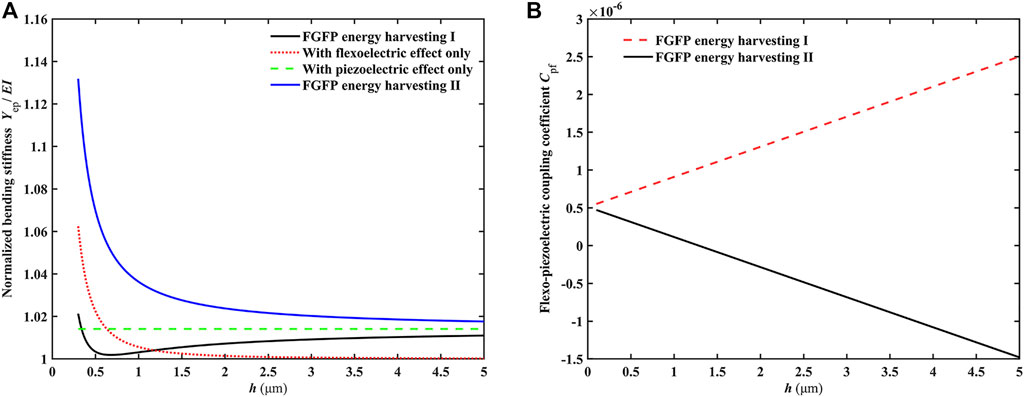
FIGURE 2. (A) Variation of
Free vibration analysis of the FGFP energy harvesting
The natural frequency of the FGFP energy harvesting is a very important physical performance. The variation of natural frequencies (
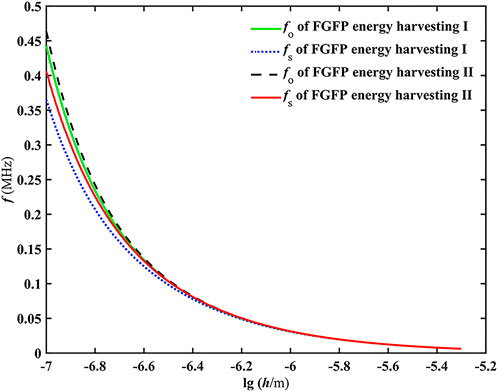
FIGURE 3. Variation of natural frequencies of the FGFP energy harvesting as a function of the beam thickness under different electrical conditions.
The natural frequency shift of beams is an important parameter for judging electromechanical coupling performance of the FGFP energy harvesting (Su et al., 2019a). Here, the effective natural frequency shift of the FGFP energy harvesting is defined as:
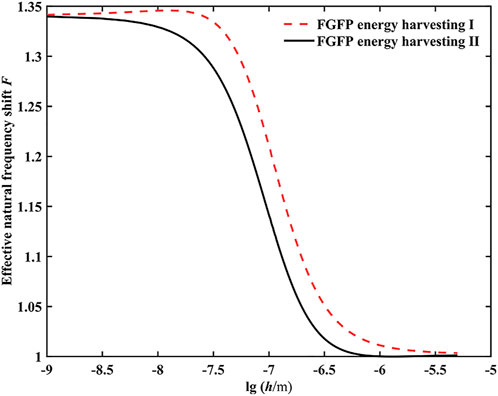
FIGURE 4. Variation of the effective natural frequency shift of two types of FGFP energy harvesting as a function of the beam thickness.
Output performance analysis of the FGFP energy harvesting
The power density response is an important parameter for evaluating the performance of the FGFP energy harvesting (Deng et al., 2014; Su et al., 2019a), which can be expressed in the following form:
where
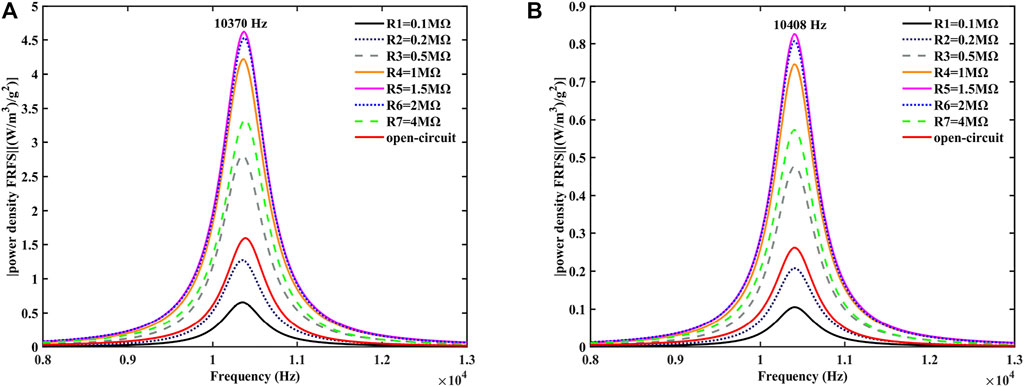
FIGURE 5. Variation of the power density FRFs of the FGFP energy harvesting with
The plotted curves in Figure 6 show the power density response for a smaller scale beam (
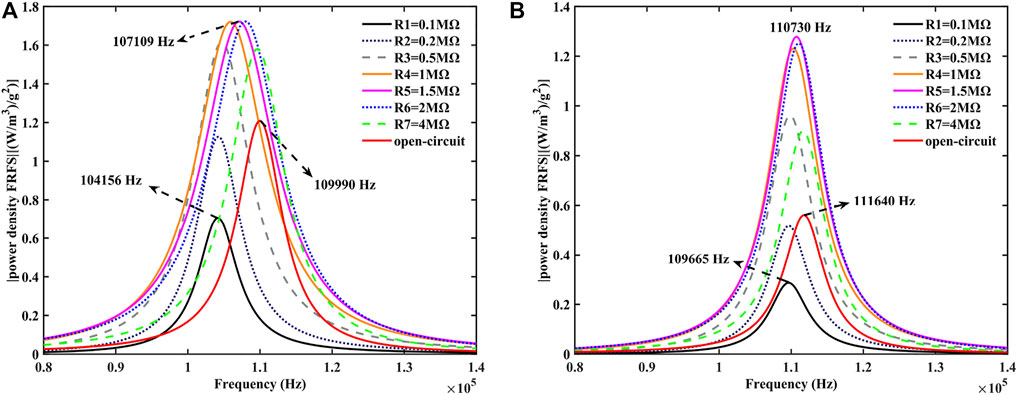
FIGURE 6. Variation of the power density FRFS of the FGFP energy harvesting with
Figure 7 presents the variation of maximum power density FRFs with the beam thickness for the different FGFP energy harvesting. The power density of the FGFP energy harvesting with only flexoelectric effect increases and then decreases with decreasing thickness. This is because when the thickness decreases to a certain value, the induced electric potential due to the flexoelectric effect will significantly act on the FGFP energy harvesting itself, resulting in a reduction on the mechanical deformation of the system, thereby reducing the mechanical vibration response of the FGFP energy harvesting. It achieves a maximum power density at about 0.4
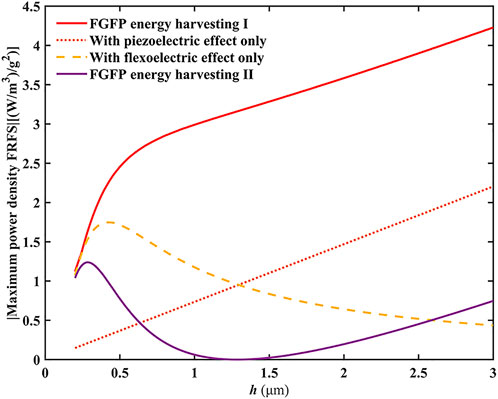
FIGURE 7. Variation of the maximum power density FRFs of two types of FGFP energy harvesting as a function of the beam thickness.
Influence of the gradient index on electromechanical coupling output of the FPFG energy harvesting
In this section, we will investigate the influence of the gradient index on the electromechanical coupling performance of the two types of FGFP energy harvesting. Keeping the bottom material (PVDF) of two types of FGFP energy harvesting invariable, we only change the parameters of the top material (BaTiO3). The top material parameter remains unchanged (
Figure 8 depicts the variation of the maximum power density FRFs with the beam thickness of two types of FGFP energy harvesting with different gradient indexes. It can be seen that the gradient index does not change the trend of the curves. The maximum power density response of the FGFP energy harvesting Ⅰ increases with increasing gradient index. The large gradient index will therefore produce more significant material gradient changes along the beam thickness. The intense flexoelectric effect and gradient piezoelectric effect will enhance the electromechanical coupling output of system at the large scale for the FGFP energy harvesting Ⅰ. For the FGFP energy harvesting Ⅱ shown in Figure 8B, the output of system generated by flexoelectric effect and gradient piezoelectric effect will cancel each other. Hence, the power density response will become very small or even zero at a certain beam thickness. At the small scale, the maximum power density response will reach a peak value at a certain thickness, which increases with increasing gradient index. At the large scale, the maximum power density response increases with increasing thickness. However, for about
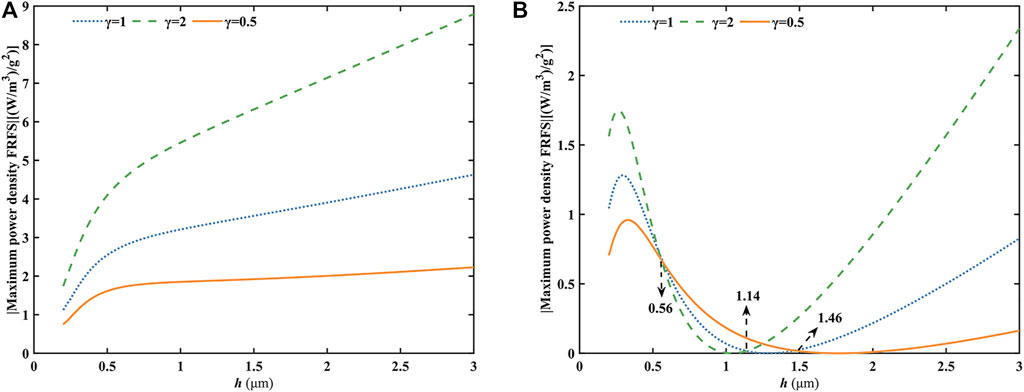
FIGURE 8. Variation of the maximum power density FRFs as a function of the beam thickness with different gradient indexes: (A) FGFP energy harvesting I; (B) FGFP energy harvesting II.
Conclusion
In this paper, the FGFP energy harvesting is studied based on the Euler-Bernoulli beam model. Utilizing the electric Gibbs free energy and the generalized Hamiltonian principle, the dynamic governing equations and boundary conditions are established. Further, the natural frequency equation is derived and the mode-superposition method is used to obtain the closed-form analytical expressions of the electromechanical responses of the FGFP energy harvesting in the modal space. The simulation results show that the change of piezoelectric polarization direction will significantly change the normalized bending stiffness and the flexo-piezoelectric coupling coefficient of the FGFP energy harvesting. Further, the piezoelectric polarization direction, gradient index, structure size and external load resistance have significant influences on the output performance of the FGFP energy harvesting. The change of piezoelectric polarization direction will lead to enhance or reduce the performance of the FGFP energy harvesting. The flexoelectric effect and gradient piezoelectric effect will dominate the output performance at the nanoscale and microscale, respectively. The present study reveals the importance of the piezoelectric polarization direction and gradient index on the output performance of the FGFP energy harvesting from nano to micro scales. This result also provides theoretical guidance for the selection of materials, gradient index, structure scale, and external load resistance to design new FGFP energy harvesting.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
ZK: Conceptualization, Mathematical modeling, Simulation test, Writing-Original Draft and Editing; ZZ: Conceptualization, Investigation, Funding acquisition, Supervision, Writing-Review and Editing.
Funding
This work was supported by Scientific and Technological Innovation Platform of Fujian Province (2006L2003).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdollahi, A., and Arias, I. (2015). Constructive and destructive interplay between piezoelectricity and flexoelectricity in flexural sensors and actuators. J. Appl. Mech. 82 (12), 121003. doi:10.1115/1.4031333
Chao, L., Tsui, C. Y., and Ki, W. H. (2007). “A batteryless vibration-based energy harvesting system for ultra low power ubiquitous applications,” in IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA, 27-30 May 2007 (IEEE), 1349–1352.
Chen, Y., Zhang, M., Su, Y., and Zhou, Z. (2021). Coupling analysis of flexoelectric effect on functionally graded piezoelectric cantilever nanobeams. Micromachines 12 (6), 595. doi:10.3390/mi12060595
Chu, L., Dui, G., and Ju, C. (2018). Flexoelectric effect on the bending and vibration responses of functionally graded piezoelectric nanobeams based on general modified strain gradient theory. Compos. Struct. 186, 39–49. doi:10.1016/j.compstruct.2017.10.083
Chu, L., Dui, G., and Zheng, Y. (2020). Thermally induced nonlinear dynamic analysis of temperature-dependent functionally graded flexoelectric nanobeams based on nonlocal simplified strain gradient elasticity theory. Eur. J. Mech. - A/Solids 82, 103999. doi:10.1016/j.euromechsol.2020.103999
Chu, L., Li, Y., and Dui, G. (2019). Size-dependent electromechanical coupling in functionally graded flexoelectric nanocylinders. Acta Mech. 230 (9), 3071–3086. doi:10.1007/s00707-019-02442-7
Cross, L. E. (2006). Flexoelectric effects: Charge separation in insulating solids subjected to elastic strain gradients. J. Mat. Sci. 41 (1), 53–63. doi:10.1007/s10853-005-5916-6
Deng, Q., Kammoun, M., Erturk, A., and Sharma, P. (2014). Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 51 (18), 3218–3225. doi:10.1016/j.ijsolstr.2014.05.018
Deng, Q. (2017). Size-dependent flexoelectric response of a truncated cone and the consequent ramifications for the experimental measurement of flexoelectric properties. J. Appl. Mech. 84 (10), 4037552. doi:10.1115/1.4037552
Erturk, A., and Inman, D. J. (2008). A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters. J. Vib. Acoustics-Transactions Asme 130 (4), 041002. doi:10.1115/1.2890402
Fu, G., and Zhou, S. (2021). On the size dependency of a dielectric partially covered laminated microbeam. Thin-Walled Struct. 161, 107489. doi:10.1016/j.tws.2021.107489
Fu, J. Y., and Cross, L. E. (2007). On the flexoelectric effects in solid dielectrics: Theories and applications. Ferroelectrics 354 (1), 238–245. doi:10.1080/00150190701455005
Fu, J., and Zhang, Z. (2022). Modeling of the bilayer piezoelectric microbeam based on the strain gradient effect. J. Appl. Phys. 131 (13), 134302. doi:10.1063/5.0084020
Hahn, M., Trolier-McKinstry, S., and Meyer, R. J. (2021). Flexoelectric barium strontium titanate (BST) hydrophones. J. Appl. Phys. 129 (6), 064504. doi:10.1063/5.0038756
Hong, J., Catalan, G., Scott, J. F., and Artacho, E. (2010). The flexoelectricity of barium and strontium titanates from first principles. J. Phys. Condens. Matter 22 (11), 112201. doi:10.1088/0953-8984/22/11/112201
Hu, S., and Shen, S. (2009). Electric field gradient theory with surface effect for nano-dielectrics. Cmc-Computers Mater. Continua 13 (1), 63–87. doi:10.3970/CMC.2009.013.063
Hudak, N. S., and Amatucci, G. G. (2008). Small-scale energy harvesting through thermoelectric, vibration, and radiofrequency power conversion. J. Appl. Phys. 103 (10), 101301. doi:10.1063/1.2918987
Ke, L. L., Yang, J., Kitipornchai, S., and Wang, Y. S. (2014). Axisymmetric postbuckling analysis of size-dependent functionally graded annular microplates using the physical neutral plane. Int. J. Eng. Sci. 81, 66–81. doi:10.1016/j.ijengsci.2014.04.005
Kumar, A., Kiran, R., Kumar, R., Chandra Jain, S., and Vaish, R. (2018). Flexoelectric effect in functionally graded materials: A numerical study. Eur. Phys. J. Plus 133 (4), 141–149. doi:10.1140/epjp/i2018-11976-1
Li, A., Zhou, S., Zhou, S., and Wang, B. (2014a). Size-dependent analysis of a three-layer microbeam including electromechanical coupling. Compos. Struct. 116, 120–127. doi:10.1016/j.compstruct.2014.05.009
Li, A., Zhou, S., Zhou, S., and Wang, B. (2014b). A size-dependent bilayered microbeam model based on strain gradient elasticity theory. Compos. Struct. 108, 259–266. doi:10.1016/j.compstruct.2013.09.020
Li, Y. S., and Pan, E. (2015). Static bending and free vibration of a functionally graded piezoelectric microplate based on the modified couple-stress theory. Int. J. Eng. Sci. 97, 40–59. doi:10.1016/j.ijengsci.2015.08.009
Liang, X., Hu, S., and Shen, S. (2014). Effects of surface and flexoelectricity on a piezoelectric nanobeam. Smart Mat. Struct. 23 (3), 035020. doi:10.1088/0964-1726/23/3/035020
Liang, X., Hu, S., and Shen, S. (2015). Size-dependent buckling and vibration behaviors of piezoelectric nanostructures due to flexoelectricity. Smart Mat. Struct. 24 (10), 105012. doi:10.1088/0964-1726/24/10/105012
Lu, C., Raghunathan, V., and Roy, K. (2011). Efficient design of micro-scale energy harvesting systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 1 (3), 254–266. doi:10.1109/jetcas.2011.2162161
Lu, J., Lv, J., Liang, X., Xu, M., and Shen, S. (2016). Improved approach to measure the direct flexoelectric coefficient of bulk polyvinylidene fluoride. J. Appl. Phys. 119 (9), 094104. doi:10.1063/1.4943069
Ma, L. S., and Lee, D. W. (2012). Exact solutions for nonlinear static responses of a shear deformable FGM beam under an in-plane thermal loading. Eur. J. Mech. - A/Solids 31 (1), 13–20. doi:10.1016/j.euromechsol.2011.06.016
Ma, W., and Cross, L. E. (2001). Large flexoelectric polarization in ceramic lead magnesium niobate. Appl. Phys. Lett. 79 (26), 4420–4422. doi:10.1063/1.1426690
Majdoub, M. S., Sharma, P., and Cagin, T. (2008). Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B 77 (12), 125424. doi:10.1103/PhysRevB.77.125424
Mbarki, R., Baccam, N., Dayal, K., and Sharma, P. (2014). Piezoelectricity above the Curie temperature? Combining flexoelectricity and functional grading to enable high-temperature electromechanical coupling. Appl. Phys. Lett. 104 (12), 122904. doi:10.1063/1.4869478
Moura, A. G., and Erturk, A. (2017). Electroelastodynamics of flexoelectric energy conversion and harvesting in elastic dielectrics. J. Appl. Phys. 121 (6), 064110. doi:10.1063/1.4976069
Nan, Z., Xie, Z., Shijie, Z., and Dejin, C. (2020). Size-dependent static bending and free vibration analysis of porous functionally graded piezoelectric nanobeams. Smart Mat. Struct. 29 (4), 045025. doi:10.1088/1361-665X/ab73e4
Poddar, S., and Ducharme, S. (2013). Measurement of the flexoelectric response in ferroelectric and relaxor polymer thin films. Appl. Phys. Lett. 103 (20), 202901. doi:10.1063/1.4829622
Qi, L., Zhou, S., and Li, A. (2016). Size-dependent bending of an electro-elastic bilayer nanobeam due to flexoelectricity and strain gradient elastic effect. Compos. Struct. 135, 167–175. doi:10.1016/j.compstruct.2015.09.020
Rafiee, M., He, X. Q., and Liew, K. M. (2014). Nonlinear analysis of piezoelectric nanocomposite energy harvesting plates. Smart Mat. Struct. 23 (6), 065001. doi:10.1088/0964-1726/23/6/065001
Rojas, E. F., Faroughi, S., Abdelkefi, A., and Park, Y. H. (2021). Investigations on the performance of piezoelectric-flexoelectric energy harvesters. Appl. Energy 288, 116611. doi:10.1016/j.apenergy.2021.116611
Sezer, N., and Koç, M. (2021). A comprehensive review on the state-of-the-art of piezoelectric energy harvesting. Nano Energy 80, 105567. doi:10.1016/j.nanoen.2020.105567
Shen, S., and Hu, S. (2010). A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 58 (5), 665–677. doi:10.1016/j.jmps.2010.03.001
Su, Y., Lin, X., Huang, R., and Zhou, Z. (2019a). Analytical electromechanical modeling of nanoscale flexoelectric energy harvesting. Appl. Sci. 9 (11), 2273. doi:10.3390/app9112273
Su, Y. X., Zhou, Z. D., and Yang, F. P. (2019b). Electromechanical analysis of bilayer piezoelectric sensors due to flexoelectricity and strain gradient elasticity. AIP Adv. 9 (1), 015207. doi:10.1063/1.5081072
Tang, L., and Wang, J. (2017). Size effect of tip mass on performance of cantilevered piezoelectric energy harvester with a dynamic magnifier. Acta Mech. 228 (11), 3997–4015. doi:10.1007/s00707-017-1910-8
Wang, G. F., and Feng, X. Q. (2010). Effect of surface stresses on the vibration and buckling of piezoelectric nanowires. EPL A Lett. J. Explor. Front. Phys. 91, 56007. doi:10.1209/0295-5075/91/56007
Wang, K. F., and Wang, B. L. (2016). An analytical model for nanoscale unimorph piezoelectric energy harvesters with flexoelectric effect. Compos. Struct. 153, 253–261. doi:10.1016/j.compstruct.2016.05.104
Yan, X., Huang, W., Ryung Kwon, S., Yang, S., Jiang, X., and Yuan, F. G. (2013). A sensor for the direct measurement of curvature based on flexoelectricity. Smart Mat. Struct. 22 (8), 085016. doi:10.1088/0964-1726/22/8/085016
Yan, Z., and Jiang, L. (2013a). Size-dependent bending and vibration behaviour of piezoelectric nanobeams due to flexoelectricity. J. Phys. D. Appl. Phys. 46 (35), 355502. doi:10.1088/0022-3727/46/35/355502
Yan, Z., and Jiang, L. Y. (2013b). Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams. J. Appl. Phys. 113 (19), 194102. doi:10.1063/1.4804949
Zhang, D. G., and Zhou, Y. H. (2008). A theoretical analysis of FGM thin plates based on physical neutral surface. Comput. Mater. Sci. 44 (2), 716–720. doi:10.1016/j.commatsci.2008.05.016
Zhang, Z., Yan, Z., and Jiang, L. (2014). Flexoelectric effect on the electroelastic responses and vibrational behaviors of a piezoelectric nanoplate. J. Appl. Phys. 116 (1), 014307. doi:10.1063/1.4886315
Zhao, X., Zheng, S., and Li, Z. (2019). Size-dependent nonlinear bending and vibration of flexoelectric nanobeam based on strain gradient theory. Smart Mat. Struct. 28 (7), 075027. doi:10.1088/1361-665X/ab1cfc
Zhou, Z. D., Yang, C. P., Su, Y. X., Huang, R., and Lin, X. L. (2017). Electromechanical coupling in piezoelectric nanobeams due to the flexoelectric effect. Smart Mat. Struct. 26 (9), 095025. doi:10.1088/1361-665X/aa7936
Keywords: functionally graded material, energy harvesting, polarization direction, flexoelectricity and piezoelectricity, electromechanical responses
Citation: Ke Z and Zhou Z (2022) Performance analysis of the functionally graded flexoelectric-piezoelectric energy harvesting. Front. Mater. 9:1097683. doi: 10.3389/fmats.2022.1097683
Received: 14 November 2022; Accepted: 07 December 2022;
Published: 20 December 2022.
Edited by:
Yunya Liu, Xiangtan University, ChinaReviewed by:
Liangliang Chu, Wuhan University of Technology, ChinaAnqing Li, Qilu University of Technology, China
Copyright © 2022 Ke and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhidong Zhou, zdzhou@xmu.edu.cn
 Zhengyu Ke
Zhengyu Ke Zhidong Zhou
Zhidong Zhou