Proposal of a turbulent Prandtl number model for Reynolds-averaged Navier–Stokes approach on the modeling of turbulent heat transfer of low-Prandtl number liquid metal

Highlights

1) Proposal of a new model for the turbulent Prandtl number in the RANS approach for engineering applications.

2) Validation of the proposed model with available LES/DNS results of the local temperature profile in the concentric annulus and bare rod bundle.

3) Validation of the proposed model with experimental correlations on the Nusselt number in a circular tube and bare rod bundle.

1 Introduction

Low-Prandtl number liquid metals are considered as promising candidate coolants in various innovative nuclear systems, such as the sodium-cooled fast reactor (SFR), the liquid lead–cooled fast reactor (LFR), and the accelerator-driven sub-critical system (ADS), due to their high molecular heat conductivity in favor of the reactors’ reliability and safety (Roelofs, 2019). With the fast development of computational power, more and more attention has been paid to applying the computational fluid dynamics (CFD) methods for detailed analysis of three-dimensional thermal–hydraulic behavior, especially in nuclear fuel assembly design (Cheng and Tak, 2006b; Marinari et al., 2019; Chai et al., 2019). However, modeling of turbulent heat flux in low-Prandtl number liquid metal flow remains a challenging task when using CFD methods to solve the turbulent flow heat transfer behavior (Shams, 2019). Advanced high-fidelity numerical approaches represented by the wall-resolved large eddy simulation (LES) method and the direct numerical simulation (DNS) method can provide detailed insight into the physics of the flow and the associated heat transfer (Tiselj et al., 2019). However, these approaches are limited to simple flow configurations and low to moderate Reynolds numbers due to their rather high requirement of computational capacities. Hence, Reynolds-averaged Navier–Stokes (RANS) method is still at least in the current state, in most cases, the only practically feasible approach to deal with high Reynolds industrial flows, especially those in complex geometries such as those encountered in typical nuclear fuel assemblies (Shams et al., 2019). It is thus important to assess and improve the accuracy of the RANS approach and the associated models for turbulent heat transfer. With this objective in mind, simulation results of the velocity and temperature field obtained by LES or DNS are, hence, very valuable references to which RANS models can be compared and calibrated.

Compared to conventional fluids with the Prandtl number in the order of unity, such as water or air, heat transfer in the low-Prandtl number liquid metal is characterized by the high contribution of molecular heat conduction even in high turbulent flow. Consequently, temperature change in the boundary layer is much smoother, even in the very thin laminar sub-layer. In the classical RANS approach with conventional turbulence models, turbulent heat transfer is often predicted solely from the knowledge of turbulent momentum transfer based on the concept of the so-called Reynolds analogy (Cheng and Tak, 2006a), in which the turbulent heat conductivity $a_t$ (or eddy conductivity) is given by the ratio between turbulent momentum conductivity ${\nu }_t$ (or eddy diffusivity) and a turbulent Prandtl number ($P{r}_t$) according to:

It is well acknowledged that an accurate prediction of $P{r}_t$ is of crucial importance in modeling turbulent heat transfer in the low-Prandtl number liquid metal flows. For instance, as pointed out by Cheng and Tak (2006b), a decrease in the Nusselt number of about 30% can be obtained by increasing $P{r}_t$ from 0.9 to 1.5. However, the conventional choice of $P{r}_t$ as a constant value of 0.85–0.9, with which satisfying results of the turbulent heat flux can be obtained for most of the engineering purposes with fluid of Prandtl number in the order of unity, is not valid for a low-Prandtl number liquid metal.

In the past, extensive studies were carried out to derive appropriate expressions for $P{r}_t$ for the low-Prandtl number liquid metal. In general, two types of models can be found in the open literature, the first type specifies $P{r}_t$ as a global value depending on the bulk flow parameters such as the bulk Reynolds number $R{e}_b$ or/and the bulk Peclet number $P{e}_b$ represented by the early model of Aoki (1963).

The models of Reynolds (1975).

Also, the model of Jischa and Rieke (1979).

The model by Cheng and Tak (2006b).

in which the constant A is given as:

The second type gives $P{r}_t$ as a local varying value depending on the local flow parameters such as the local eddy diffusivity, represented by the model of Kays (1994).

where the turbulent Peclet number Pe_t is defined as:

Figure 1 compares the $P{r}_t$ calculated with the model of Aoki (1963), Reynolds (1975), Jischa and Rieke (1979), and Cheng and Tak (2006b) for bulk Peclet number $P{e}_b$ up to 2,800 at $Pr$ of 0.01 (corresponding to a $R{e}_b$ up to 280,000). Also included in the figure is the proposed model for $P{r}_t$ in the current study given by Eq. 21. It is observed that first, $P{r}_t$ generally decreases with increasing $P{e}_b$. Second, $P{r}_t$ tends to approach a constant value between 1 and 2 as $P{e}_b$ becomes larger than 2000 except for the model of Cheng and Tak (2006b). $P{r}_t$ predicted by the model of Cheng and Tak (2006b) is generally larger than all the other models. Finally, a rather scattering distribution exists in the predicted values of $P{r}_t$ obtained by different models proposed in the literature, especially in the range of $P{e}_b$ lower than 1,000. A possible reason for the scattering is due to the lack of reliable and consistent experimental data on turbulent heat transfer in liquid metal flows.

FIGURE 1. Comparison of turbulent Prandtl numbers obtained with different models (molecular Prandtl Pr = 0.01).

With the fast-growing computational capacities, advanced high-fidelity numerical approaches such as wall-resolved LES method and DNS method become more and more attractive to provide detailed insight into the physics of the flow and the associated heat transfer. Due to their high demands of computational capacities, LES and DNS simulations are often, at least in the current state, limited to rather simple geometrical configurations. Nevertheless, simulation results of LES and DNS are very valuable references to which RANS models can be compared and calibrated. In the current study, LES and DNS results of a simple fully developed forced turbulent channel flow of low-Prandtl number fluid $(Pr=0.01$ and $0.025$) up to $R{e}_{\tau }$ of $2000$ were used as references to assess RANS modeling of the turbulent heat transfer by means of the turbulent Prandtl number concept. RANS simulations of the forced turbulent channel flow with boundary conditions following those in LES/DNS settings were performed by systematically varying $P{r}_t$ from 0.9 up to 8.0. Based on the comparison of the dimensionless temperature field and/or bulk Nusselt number $N{u}_b$ calculated by the RANS approach with those obtained by LES/DNS simulations, an appropriate choice of the $P{r}_t$ associated with the RANS approach can be obtained and a new model for $P{r}_t$ was then proposed and validated.

2 Large eddy simulation and direct numerical simulation results on fully developed forced turbulent channel flow of low-Prandtl number fluid

As depicted in Figure 2, a fully developed forced turbulent channel flow of low-Prandtl number fluid heated by a uniform heat flux $q_w$ on both walls is a simple scenario which has been extensively investigated in the open literature by means of LES and DNS. Table 1 summarizes the representative LES and DNS simulations in the ascending order of the bulk Peclet number $P{e}_b$. The channel flow is characterized by the friction Reynolds number $R{e}_{\tau }$ which is defined with the friction velocity $u_{\tau }$ and the channel half height $\delta$ according to:

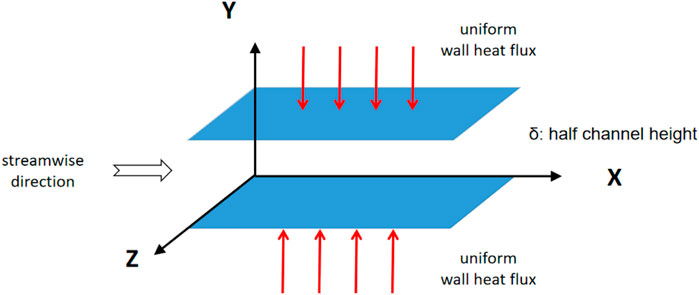
FIGURE 2. Sketch of the fully developed forced turbulent channel flow heated by a uniform heat flux $q_w$ on both sides of the walls.

TABLE 1. Summary of LES/DNS simulation on fully developed turbulent channel flow for low-Prandtl number fluid.

in which the friction velocity $u_{\tau }$ is defined with relation to the wall shear stress ${\tau }_w$ as:

where $\rho$ and $\mu$ stand for the fluid density and dynamic viscosity, respectively. The bulk velocity $u_b$ is an average channel flow velocity defined as:

which is then used to define the bulk Reynolds number $R{e}_b$ as:

The bulk Peclet number $P{e}_b$ is defined as:

Also included in Table 1 is the global heat transfer performance characterized by the bulk Nusselt number $N{u}_b$ defined as:

where the bulk temperature $T_b$ is the average channel flow temperature which is defined as:

For the purpose of assessing RANS approach, DNS results of Kawamura et al. (1999) with $Pr=0.025$ and $R{e}_{\tau }=180,395$, DNS results of Abe et al. (2004) with $Pr=0.025$ and $R{e}_{\tau }=1020$, as well as DNS results of Bricteux et al. (2012) with $Pr=0.01$ and $R{e}_{\tau }=180,590$, LES results of Duponcheel et al. (2014) with $Pr=0.01, 0.025$ and $R{e}_{\tau }=2000$ were chosen as references. The corresponding bulk Reynolds number $R{e}_b$ covers a wide range from 5,600 up to 87,000, while the bulk Peclet number $P{e}_b$ is varied in the range from 56 up to 2,175.

3 Reynolds-averaged Navier–Stokes approach associated with turbulent Prandtl number concept

3.1 Geometrical setups and boundary conditions

As depicted in Figure 3, a quasi-2D RANS simulation of the fully developed channel flow was performed in the current study with the commercial CFD software package Ansys CFX. An arbitrary channel half height $\delta$ of 0.01 m (y-direction) was chosen, while the channel streamwise (x-direction) length was set as 80 times of $\delta$. For a quasi-2D simulation, only 1 cell element was extruded in the spanwise direction (z-direction) and symmetrical conditions were specified on the two boundaries of the spanwise direction. A translational periodic boundary condition was specified on the two boundaries of the streamwise direction, in order to obtain the fully developed flow conditions. A constant uniform heat flux was given for the top and bottom boundaries following the LES/DNS settings.

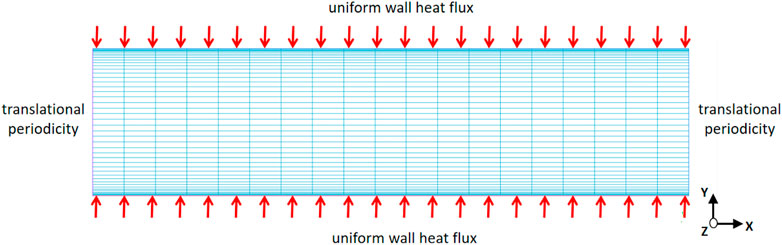
FIGURE 3. Sketch of the mesh structure and boundary conditions used in RANS simulation of the fully developed forced turbulent channel flow.

Table 2 summarizes the most important boundary parameters of the RANS simulations performed in the current study. The flow is assumed to be incompressible with constant thermal–physical properties as in consistency with the LES/DNS settings. The governing equations are the RANS equations for incompressible flow with constant thermal–physical properties and the energy conservation equation for temperature. Due to the periodic boundary condition in the streamwise direction and the constant wall heat flux on the top and bottom walls, the temperature will continuously increase in the streamwise direction and a fully developed flow condition will never be achieved. Therefore, a negative volumetric heat source was specified in the RANS simulation, which takes exactly the same amount of energy away as given to the domain by the heat flux on the top and bottom walls. High-resolution advection scheme and turbulence numerics were chosen to ensure a second order accuracy. The buoyancy effect due to the temperature difference in the channel height direction (y-direction) is negligibly small, hence not considered in the RANS simulations. This is justified by the fact that the bulk Richardson number $R{i}_b$ for the RANS setups according to the following equation is quite small (<<1):

TABLE 2. Summary of boundary parameters for RANS simulations of fully developed forced turbulent channel flow for low-Prandtl number fluid.

where $g$ and $\beta$ are the gravitational acceleration and the thermal expansivity, respectively.

3.2 Presentation of the Reynolds-averaged Navier–Stokes results: normalization in friction units

The mean streamwise velocity profile and mean temperature profile in the channel height direction (y-direction) are normalized with the friction velocity $u_{\tau }$ and friction temperature $T_{\tau }$, respectively. The friction velocity is already defined in Eq. 10 with relation to the wall shear stress ${\tau }_w$. The friction temperature $T_{\tau }$ is defined with relation to the wall heat flux $q_w$ as follows:

where $c_p$ stands for the specific heat capacity at constant pressure.

The mean streamwise velocity profile is hence characterized by the normalized dimensionless mean velocity $u^{+}$ given as:

The mean temperature profile is characterized by the normalized dimensionless mean temperature ${\theta }^{+}$ according to:

where $T_w$ is the wall temperature of the heated top or bottom wall. Both the dimensionless velocity and dimensionless temperature profile are specified in terms of a dimensionless universal wall distance $y^{+}$ defined as:

where y is the actual distance to the wall.

3.3 Effect of mesh refinement and turbulence model

As also included in Figure 3, a block-structured mesh consisting of only hexahedra was used in RANS simulations. The mesh nodes are uniformly distributed among the streamwise direction (x-direction), while local refinement was specified in the y-direction when approaching the top and bottom wall, in order to ensure at least a dimensionless universal wall distance of the first interior node $y_1^{+}<1$ as required for the wall-resolved low-Reynolds number turbulence model in RANS simulations, that is, the $k-\omega$ model and the shear stress transport (SST) model. The mesh sensitivity study was performed for the LES case of $Pr=0.01$ and $R{e}_{\tau }=2000$ (Duponcheel et al., 2014) (corresponding $R{e}_b$ and $P{e}_b$ are 87,000 and 870, respectively). The wall-resolved $k-\omega$ turbulence model and a constant turbulent Prandtl number $P{r}_t$ of 2.0 were used for all the tested meshes. For the mesh sensitivity study, three different levels of mesh refinement were studied with the same block structure as displayed in Figure 3. The total cell numbers of the three meshes were 3,713, 5,841, and 15,721, respectively, meaning that the highest density mesh is 4.23 times finer than the smallest-density mesh. The corresponding values of $y_1^{+}$ were 0.6, 0.2, and 0.1, respectively.

Figure 4 compares the normalized mean streamwise velocity profile ($u^{+}$) and the normalized mean temperature profile (${\theta }^{+}$) obtained with the three tested meshes. It is observed that the mean streamwise velocity calculated with mesh 1 is slightly higher than that obtained with mesh 2 and mesh 3 in the near wall region with $y^{+}$ lower than 5, while the difference among the velocity profile obtained with mesh 2 and mesh 3 is negligibly small. Furthermore, the mean temperature profile obtained with the three tested meshes agrees well with each other, despite a large difference in the total cell number and mesh refinement. The bulk Nusselt number $N{u}_b$ obtained by RANS simulations with the three different meshes are 8.81, 8.81, and 8.84, respectively. In conclusion, mesh 2 with $y_1^{+}$ of 0.2 was hence chosen for the RANS simulations henceforth in the current study.

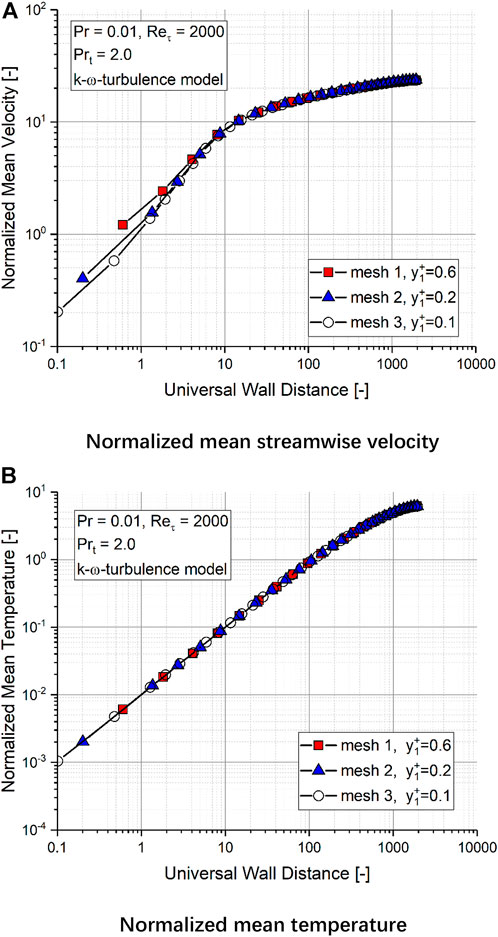
FIGURE 4. Mesh sensitivity study: comparison of the (A) mean velocity profile and (B) mean temperature profile normalized in a friction unit obtained with different meshes.

Two types of turbulence models are available in CFX, that is, the wall-resolved low-Reynolds number turbulence model with which the boundary layer is fully resolved, and the wall-unresolved high-Reynolds number turbulence model with which the boundary layer is approximated relying on a logarithmic wall function. For the present analysis, the wall-resolved $k-\omega$ and $SST$ turbulence model as well as the wall-unresolved $k-\mathit{ϵ}$ turbulence model were tested. Figure 5 shows the mean streamwise velocity profile and the mean temperature profile normalized in fiction unit for the case of $Pr=0.01$ and $R{e}_{\tau }=2000$. A constant turbulent Prandtl number $P{r}_t$ of 2.0 was specified for all the RANS simulations. It is observed that the temperature profile is hardly influenced by the turbulence model. In the logarithmic region where $y^{+}$ becomes larger than 60, the velocity profile calculated by the different turbulence model agrees well with each other. The difference in the velocity profile in the near wall region ($y^{+}<30$) is to be expected, since the $k-\mathit{ϵ}$ model applies the logarithmic wall function for the complete boundary layer. The bulk Nusselt numbers $N{u}_b$ obtained with $k-\mathit{ϵ}$, $k-\omega$, and SST model are 8.72, 8.81, and 8.84, respectively. The $k-\omega$ turbulence model was chosen for the RANS simulations henceforth in the current study.

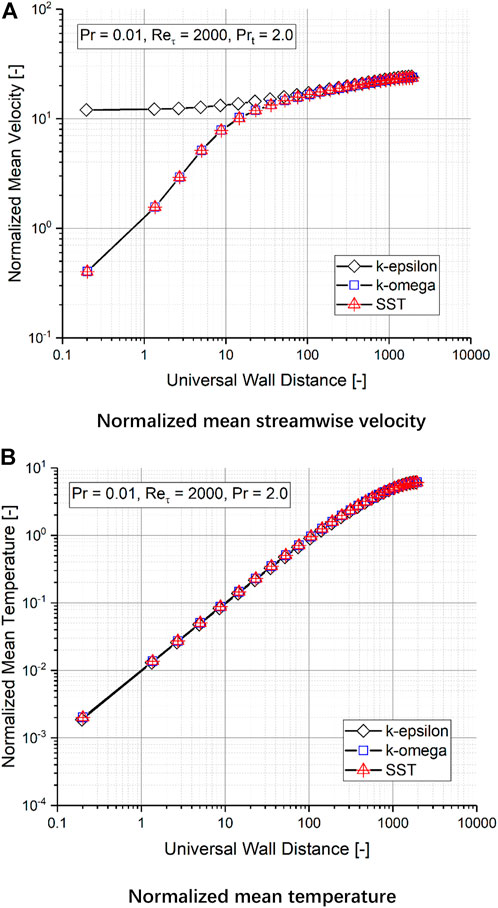
FIGURE 5. Effect of different turbulence models on (A) mean velocity and, (B) mean temperature profile in friction unit.

3.4 Effect of turbulent Prandtl number $\mathit{P}{\mathit{r}}_{\mathit{t}}$

To study the effect of the turbulent Prandtl number $P{r}_t$, the same case of $Pr=0.01$ at $R{e}_{\tau }=2000$ as in the mesh sensitivity study was further investigated. In the RANS simulations, $P{r}_t$ was systematically varied from 0.9, 1.2, 1.5, 2.0, 2.5, 3.0, 3.5 up to 4.0. The same mesh with $y_1^{+}$ of 0.2 (mesh 2) and the same $k-\omega$ turbulence model were employed. Since the velocity field is hardly affected by $P{r}_t$ for incompressible flow with constant thermal–physical properties, Figure 6A shows only the normalized mean temperature profile obtained by the RANS simulations. For a better demonstration of the results, only RANS results of $P{r}_t$= 0.9, 2.0, and 4.0 are shown in the figure (the RANS simulation results with the optimum value of $P{r}_t$ = 2.3 are also included in Figure 6A and will be discussed later.). The corresponding LES results obtained by Duponcheel et al. (2014) are shown as a straight line in the subfigure for comparison with RANS results. Also included in the figure is the theoretical linear law of the temperature profile ${\theta }^{+}=Pr\cdot y^{+}$ (dashed line) (Kader, 1981). It is shown as follows:

1) Compared to conventional fluid with the Prandtl number in the order of unity, for which the linear law is valid only in the very thin laminar sub-layer of $y^{+}$ generally much smaller than 30, the theoretical linear law is still valid at a wall distance of $y^{+}$ up to 60∼70 for low-Prandtl number fluid. This indicates that the heat transfer in this region is dominated by the molecular effect of heat conduction. Consequently, no difference can be observed in the temperature profiles obtained with RANS of different $P{r}_t$ and they all agree well with the temperature profile obtained by LES.

2) As $y^{+}$ becomes larger than 100, the theoretical linear law is no longer valid. The temperature profile given by the linear law is much steeper than that calculated by LES, which indicates that the turbulent diffusivity also becomes important in the heat transfer in addition to the molecular effect of heat conduction. It is clearly seen that the temperature profile now depends strongly on $P{r}_t$. The temperature profile obtained with the conventional choice of $P{r}_t$= 0.9 is much smoother than that calculated by LES, which indicates that the global heat transfer, that is, the heat transfer contribution due to turbulent diffusivity is obviously overestimated. With $P{r}_t$ increasing from 0.9 to 1.5 and 4.0, the temperature profile becomes steeper and an optimum value of $P{r}_t$ for the RANS approach exists apparently in the range of 1.5–4.0.

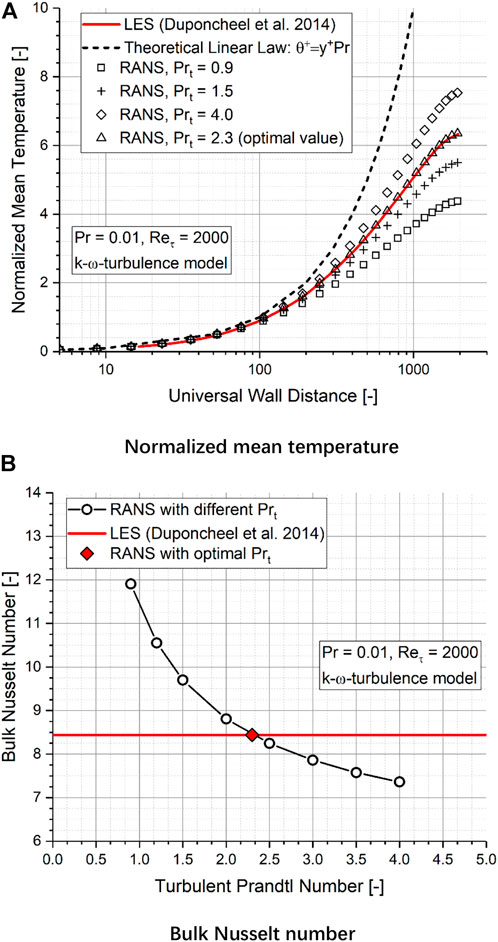
FIGURE 6. RANS approach with varying turbulent Prandtl numbers: (A) effect on normalized mean temperature; (B) effect on bulk Nusselt number.

In order to obtain the optimum value of $P{r}_t$ for the investigated case of Pr = 0.01 at Reτ = 2000, the global heat transfer behavior was also studied. Figure 6B shows the bulk Nusselt number $N{u}_b$ obtained in the RANS simulations with different $P{r}_t$ (shown as line with circular symbols), compared with that obtained by LES (red straight line) of Duponcheel et al. (2014). It is observed that with $P{r}_t$ = 0.9, the bulk Reynolds number was overestimated by about 40%. The conventional choice of $P{r}_t=0.9$ is clearly not valid for low-Prandtl number fluid. The bulk Nusselt number $N{u}_b$ decreases with increasing turbulent Prandtl number $P{r}_t$ and an optimum value of $P{r}_t$ is apparently located in the interval between 2.0 and 2.5. Therefore, further RANS simulations with $P{r}_t$ = 2.1, 2.2, 2.3, and 2.4 were carried out and the optimum value was finally found at $P{r}_t=2.3$ (shown as the diamond symbol in Figure 6B), for this value; the $N{u}_b$ obtained by RANS simulation is equal to that obtained by LES. The temperature profile obtained with $P{r}_t=2.3$ was also included in Figure 6A with triangular symbols and it agrees well with that obtained by LES (straight line).

4 Development of a new turbulent Prandtl number model for Reynolds-averaged Navier–Stokes approach

4.1 Proposal of a new turbulent Prandtl number model for Reynolds-averaged Navier–Stokes approach

The aforementioned approach to determine the optimum value of $P{r}_t$ for the RANS approach was also conducted for further selected LES/DNS cases listed in Table 1, for which the bulk Nusselt numbers $N{u}_b$ were reported in the respective sources, that is, for the case with $Pr=0.01$ at $R{e}_{\tau }=590$ (Bricteux et al., 2012) and for the case with $Pr=0.025$ at $R{e}_{\tau }=2000$ (Duponcheel et al., 2014). For the purpose of developing a suitable model for $P{r}_t$, RANS simulations were also performed for the case with $Pr=0.01$ at $R{e}_{\tau }=180$ (Bricteux et al., 2012) and for the case with $Pr=0.025$ at $R{e}_{\tau }=1020$ (Abe et al., 2004). Although no values of $N{u}_b$ were provided in the DNS simulations of the aforementioned two cases, the optimum value of $P{r}_t$ for the RANS simulation was found solely by comparing the temperature profile. Overall, RANS simulations were performed for five cases of different $Pr$ and $R{e}_{\tau }$ (corresponding $R{e}_b$ and $P{e}_b$ covering the range from 5,600 to 87,000 and from 140 to 2,175, respectively). By comparing the temperature profile or/and bulk Nusselt number obtained in RANS simulations with those obtained in their respective LES/DNS simulations, the optimum values of $P{r}_t$ for the RANS approach were determined for the five cases, as shown with the five circular symbols in Figure 7.

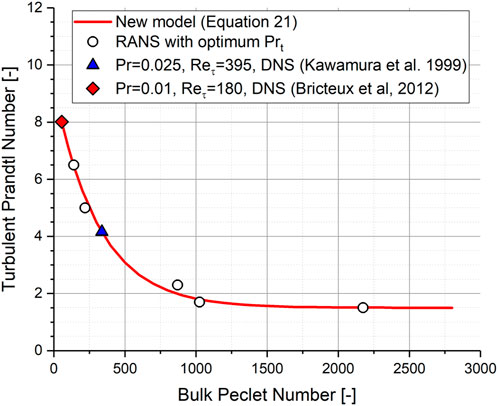
FIGURE 7. Development of a new model of the turbulent Prandtl number for RANS with LES/DNS results in turbulent channel flow as a reference.

It is observed that

1) Apparently, the turbulent Prandtl number $P{r}_t$ can be correlated solely with the bulk Peclet number $P{e}_b$ independent of Prandtl number $Pr$.

2) Furthermore, $P{r}_t$ decreases with increasing $P{e}_b$ and tends to approach a constant value of 1.5 when $P{e}_b$ becomes larger than 2000. This behavior is in general agreement with other models proposed in the literature as shown in Figure 1.

3) More importantly, the fact that $P{r}_t$ approaches a constant value for large bulk Peclet number $P{e}_b$ (corresponding also to a large bulk Reynolds number $R{e}_b$) means that no further LES/DNS simulations are required for those large Reynolds numbers when developing a suitable model for $P{r}_t$.

4) Therefore, the following simple model for $P{r}_t$ was proposed for the usage in the RANS approach, in which $P{r}_t$ was assumed as a function of the bulk Peclet number $P{e}_b$ (shown with the red straight line in Figure 7).

5) Since the proposed new model in Eq. 21 was derived based on LES/DNS results, the validity range of the new model should be limited to the range as specified in LES/DNS simulations as summarized in Table 1. Therefore, the validity range of $P{e}_b$ should be from 56 to 2,175 with a validity range of $Pr$ from 0.025 to 0.01.

For assessment of the proposed model for the turbulent Prandtl number, RANS simulation was performed with $P{r}_t$ calculated from the new model for the case of $Pr=0.01$ at $R{e}_{\tau }=180$ (corresponding bulk Reynolds number $R{e}_b$ is 5,600 and bulk Peclet number $P{e}_b$ is 56) for which DNS results of the temperature profile are given in Bricteux et al. (2012), and for the case of $Pr=0.025$ at $R{e}_{\tau }=395$ (corresponding $R{e}_b$ is 13,500 and $P{e}_b$ is 337.5), for which DNS results of the temperature profile are given in Kawamura et al. (1999). In the RANS simulations, $P{r}_t$ was then calculated with the proposed model given by Eq. 21. For the case of $Pr=0.025$ at $R{e}_{\tau }=395$, the $P{r}_t$ calculated with the proposed model is 4.15, while for the case of $Pr=0.01$ at $R{e}_{\tau }=180$ the calculated $P{r}_t$ is 7.98. Figure 8 compares the two cases of the normalized temperature profiles calculated by RANS simulations with those obtained by their respective DNS simulations. It is observed that, despite the fact that only five points were used to develop the new model for $P{r}_t$, the agreement between the RANS and DNS results is acceptable, which justifies the adequacy of the proposed model.

FIGURE 8. Assessment of the proposed model for the turbulent Prandtl number with DNS results for Pr = 0.025 at Reτ = 395, and for Pr = 0.01 at Reτ = 180: comparison of the mean temperature profile normalized in a friction unit.

4.2 Validation of the proposed turbulent Prandtl number model for Reynolds-averaged Navier–Stokes approach

The general strategy for validation of the proposed new model for the turbulent Prandtl number for the RANS approach is divided into the following two phases:

1) Phase I: taking LES/DNS results on the local temperature profile in the concentric annulus and bare rod bundle heated by constant uniform heat flux as a reference, with which RANS simulations results with the new model for $P{r}_t$ will be compared. In the current study, we chose the LES/DNS simulation performed in a concentric annular channel by Lyu et al. (2015) and Marocco (2018) with a bulk Reynolds number of 8,900 at $Pr=0.026$ and the LES simulation performed in a bare rod bundle by Shams et al. (2018) with a bulk Reynolds number of $54650$ at $Pr=0.016$ as a reference.

2) Phase II: LES/DNS simulations in the concentric annulus and bare rod bundle can provide detailed information about the local temperature profile, but are only available to a rather low-Reynolds number and Peclet number due to the enormous computational requirement. From the engineering point of view, the most important parameter to be considered is the heat transfer behavior in terms of the bulk Nusselt number $N{u}_b$. Therefore, in the second phase of the validation process, experimental correlations on the bulk Nusselt number $N{u}_b$ developed for a circular tube and bare triangular rod bundle were taken as a reference, with which RANS simulations results with the new model for $P{r}_t$ will be compared. The reason for selecting a circular tube and bare triangular rod bundle lies mainly in the fact, that most of the experimental investigations on turbulent heat transfer with the low-Prandtl number liquid metal were actually conducted with these two kinds of geometries and various experimental correlations were available in the open literature as summarized in OECD (2015).

4.2.1 Phase I: validation based on large eddy simulation/direct numerical simulation results for a local temperature profile in the concentric annulus and bare rod bundle

As the first step of the validation process phase I, a concentric annular channel heated on both walls as depicted in Figure 9A was considered due to its closeness to the sub-channel in a bare rod bundle (Ma et al., 2012). LES/DNS simulations on the fully developed state of turbulent heat transfer in the annular channel were performed at $Pr=0.026$ with a bulk Reynolds number $R{e}_b=8900$ by Lyu et al. (2015) and Marocco (2018). The ratio of the outer diameter $R_o$ to the inner diameter $R_i$ is 2. In the LES simulation, the annular channel was heated with a constant uniform heat flux on both walls. Since the flow and heat transfer situation on the inner wall is closer to that in a rod bundle, only the LES results normalized based on the parameters of the inner wall were taken as a reference.

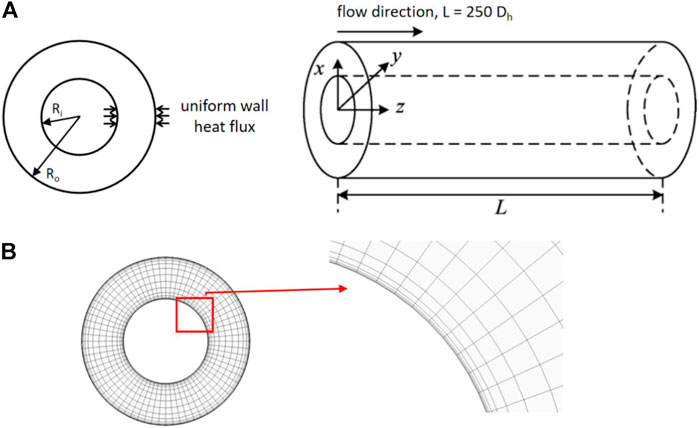
FIGURE 9. (A) Sketch of a concentric annular channel heated uniformly on both walls and (B) mesh used in the RANS simulations.

Following the LES setting, RANS simulation was performed with the $P{r}_t$ given by the new model proposed in the current study. With $Pr=0.026$ at $R{e}_b=8900$, the corresponding bulk Peclet number $P{e}_b$ is 231 and the turbulent Prandtl number $P{r}_t$ calculated with the new model is hence 5.2. Lead–bismuth eutectic (LBE) with constant thermal–physical properties taken from the OECD Handbook on a heavy liquid metal (OECD, 2015) was chosen as a working fluid. An arbitrary inner diameter $R_i$ of 10 mm was chosen for the RANS simulation, while the outer diameter $R_o$ is 20 mm following the setting in the LES simulation. The hydraulic diameter of the annular channel is then 10 mm. The channel length in the flow direction $L$ was set as 250 times of the channel hydraulic meter in the RANS simulations, in order to assure the establishment of a fully developed state in the channel. Constant and uniform velocity and temperature were given to the inlet boundary, while a constant pressure was specified at the outlet boundary. Both inner and outer walls of the annular channel were modeled as no-slip walls for the velocity field and a constant uniform heat flux was imposed for the temperature field. Also included in Figure 9B is the detail of the mesh structure in RANS simulation. As recommended in the mesh sensitivity study in Section 3.3, the block-structured hexahedral mesh was used with local refinement close to both heated walls.

Figure 10 shows the fully developed normalized mean temperature profile in the radial direction of the annular channel. The wall distance was determined relative to the inner wall and the mean temperature was also normalized with friction temperature and wall temperature on the inner wall. It is observed that the temperature profile obtained by the RANS simulation with the new model for $P{r}_t$ agrees well with that given by LES simulation in the literature (Lyu et al., 2015; Marocco, 2018). RANS simulation with the Kays model, which gives local varying $P{r}_t$ depending on local flow parameters (Eq. 7), was also performed. As depicted in Figure 10, temperature profiles predicted by the Kays model and by the new model proposed in this study agree well with each other.

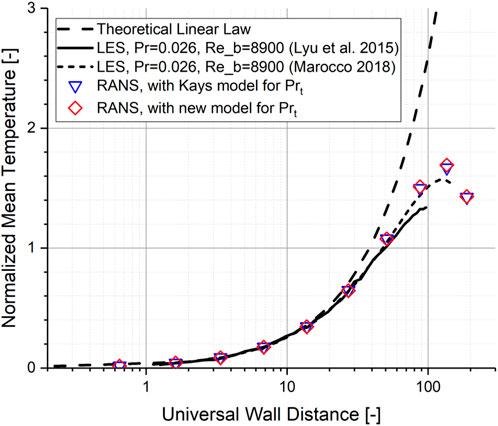
FIGURE 10. Validation of the proposed model on turbulent Prandtl number: a heated concentric annular channel.

A further validation of the proposed new model for the turbulent Prandtl number was performed in a loosely spaced bare rod bundle, for which wall-resolved large eddy simulation (LES) on the fully developed state of turbulent heat transfer with liquid lead at an operating temperature of 440°C (corresponding to a $Pr=0.016$) was performed at a bulk Reynolds number of 54,650 (Shams et al., 2018). As depicted in Figure 11A, the diameter (D) of the rod is 10.5 mm and the pitch (P) between the rods is 13.86 mm, corresponding to a pitch-to-diameter ratio $P/D$ of 1.32. The computational domain consists of two adjacent sub-channels with a hydraulic diameter of 9.67 mm. Liquid lead with constant thermal–physical properties at 440°C is considered as a working fluid. In the RANS simulation, the channel flow length was set at 300 times of the hydraulic diameter for the establishment of a fully developed state. All the rods were modeled as no-slip walls imposed with a constant uniform wall heat flux. Following the LES settings, the arrows of the same color (Figure 11A) indicate that the side planes have been connected with the periodic boundary conditions. Also included in Figure 11B is the block-structured mesh used in the RANS simulation, following the recommendation derived from the mesh sensitivity study in Section 3.3.

FIGURE 11. (A) Sketch of a hexagonal rod bundle heated uniformly on walls and (B) mesh used in the RANS simulations.

Figure 12 compares, then, the fully developed temperature profile in the gap region of the two sub-channels (as indicated with a red arrow in Figure 11A). It is observed that the temperature profile obtained by RANS simulation with the new model for $P{r}_t$ agrees well with that provided by LES (Shams et al., 2018). Similar to the case in the annular channel, temperature profiles predicted by the Kays model and by the new model proposed in this study agree well with each other.

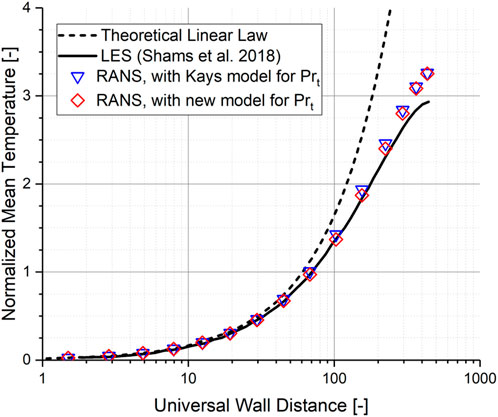
FIGURE 12. Validation of the proposed model on the turbulent Prandtl number: a hexagonal rod bundle.

4.2.2 Phase II: validation based on experimental correlations for the Nusselt number in a circular tube and bare rod bundle

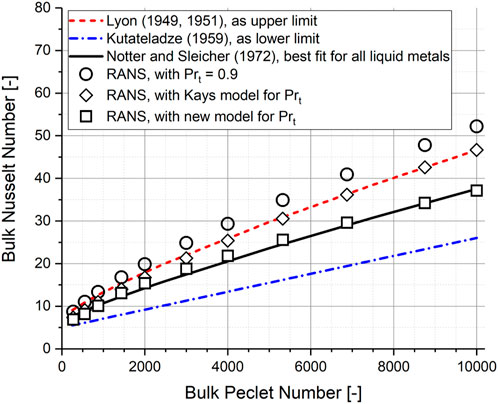
The first step of validation phase II was performed in a circular tube, for this geometry has been studied intensively from an experimental point of view. Many correlations on the turbulent heat transfer behavior (in terms of the bulk Nusselt number $N{u}_b$) are available in the open literature. However, a common agreement is not yet available, as often contradictory conclusions were reported by different authors (OECD, 2015). We take, as recommended in the OECD Handbook on the heavy liquid metal (OECD, 2015) based on a critical review of the available literature for the experimental data and proposed correlations, the following three correlations as references for comparison with RANS results. All the correlations predict the heat transfer behavior of liquid metal in a similar way as represented by the bulk Nusselt number $N{u}_b$ and bulk Peclet number $P{e}_b$.

1) Correlation of Lyon (1949), Lyon (1951) as an upper limit for the bulk Nusselt number.

2) Correlation of Kutateladze et al. (1959) as a lower limit for the bulk Nusselt number.

3) Correlation of Notter and Sleicher (1972) as the best general applicable correlation for all the investigated liquid metals including sodium (Na) and sodium–potassium alloys (NaK), pure lead (Pb), and lead–bismuth eutectic (LBE) as well as pure mercury (Hg).

It should be noted that all the aforementioned correlations were proposed for the thermal boundary condition of the uniform wall heat flux and have been developed for fully developed turbulent flow conditions with bulk Reynolds numbers $R{e}_b$ in the range between ${10}^4$ and ${10}^6$. As depicted in Figure 13, RANS simulations were, hence, performed in a circular tube heated with a uniform wall heat flux. Constant uniform velocity and inlet temperature were given at the inlet boundary, while a constant pressure boundary condition was set at the outlet boundary. In order to achieve the fully developed state, the streamwise length of the tube was set as 250 times of the tube diameter. RANS simulations were performed for a lead–bismuth eutectic (LBE) with constant thermal–physical properties at $Pr=0.025$. The bulk Reynolds number $R{e}_b$ determined with the bulk flow velocity of the tube, covers a wide range between ${10}^4$ and $4 \times {10}^5$, while the corresponding bulk Peclet number $P{e}_b$ varies between 250 and 1,000. The block-structured mesh with local refinement toward the heated tube wall was used in all the RANS simulations, in accordance with the recommendation given by the mesh sensitivity study in Section 3.3.

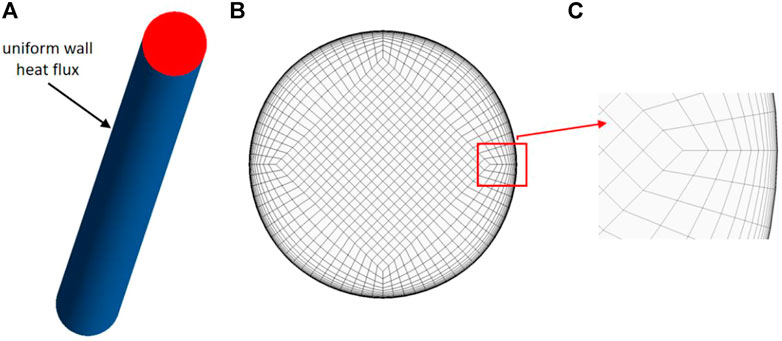
FIGURE 13. (A) Sketch of a tube heated uniformly on the wall; (B) and (C) mesh used in the RANS simulations.

Figure 14 compares then the bulk Nusselt number $N{u}_b$ obtained in RANS simulations with that calculated with the experimental correlations of Eqs. 22–24. With the conventional choice of $P{r}_t=0.9$, the bulk Nusselt number is largely overpredicted. RANS simulations with the Kays model for $P{r}_t$ still overpredict the bulk Nusselt number, since a good agreement with the upper limit defined by the correlation of Lyon (1949), Lyon (1951) is observed. With the proposed new model for $P{r}_t$, on the other hand, a much better agreement with the experimental correlations is achieved. The bulk Nusselt number $N{u}_b$ obtained with the proposed new model for $P{r}_t$ lies within the range of the upper and lower limit defined by the correlation of Lyon (1949), Lyon (1951), and Kutateladze et al. (1959), respectively, and it agrees well with that given by the correlation of Notter and Sleicher (1972), which is recommended as the best general applicable correlation for all the investigated liquid metals including sodium (Na) and sodium–potassium alloys (NaK), pure lead (Pb) and lead–bismuth eutectic (LBE) as well as pure mercury (Hg).

FIGURE 14. Validation of the proposed model on the turbulent Prandtl number: heated tube.

In the second step of validation phase II, a bare rod bundle in the hexagonal arrangement was investigated, for which most of the experiments were performed in hexagonal arrays or bundles (OECD, 2015). Based on a review of available experimental data, the following three correlations were chosen as references. All the correlations express the bulk Nusselt number $N{u}_b$ in a similar way in terms of the bulk Peclet number $P{e}_b$ and the pitch-to-diameter ratio ($P/D$).

1) Correlation of Gräber and Rieger (1972).

2) Correlation of Ushakov et al. (1977).

3) Correlation of Mikityuk (2009).

It should be noted, that the aforementioned Eqs. 25–27 were developed based on the experimental data of alkali metals such as liquid sodium (Na) or sodium–potassium alloy (NaK). However, as reviewed by Mikityuk (2009), the three correlations were recommended in the OECD Handbook on the heavy liquid metal (OECD, 2015) as the most relevant engineering heat transfer correlations for heavy liquid metal flows, that is, LBE or liquid lead. Similar to the correlations proposed for a circular tube, the aforementioned three correlations for the bare rod bundle are defined for the fully developed state. Table 3 summarizes the validity range of the respective correlations in terms of the pitch-to-diameter ratio and bulk Peclet number. However, it should be noted that in the review conducted by Mikityuk (2009), all the three correlations were recommended for use in the range of $P/D=1.1\sim 1.95$ and bulk Peclet number $P{e}_b$ of $30\sim 5000$.

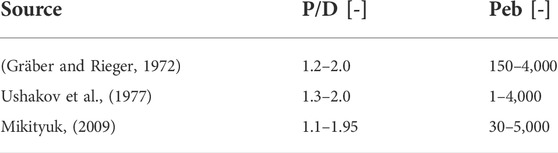
TABLE 3. Summary of experimental correlations on the bulk Nusselt number in a bare rod bundle of the hexagonal arrangement for the low-Prandtl number liquid metal.

Figure 15A defines the geometry investigated in the current study, where a triangular bundle configuration is shown. One-sixth of a sub-channel (a colored region in the figure) was defined as a computational domain, in which a block-structured hexahedral mesh was defined (Figure 15B). The definition of the boundary conditions was specified in Figure 15C. The rod was defined as a no-slip wall with a constant uniform heat flux, while the symmetry boundary condition was imposed on the other three side planes. In order to achieve a fully developed state, a domain length of 300 times of the hydraulic diameter was given in the flow direction. Constant uniform velocity and temperature were specified in the inlet boundary and a constant pressure condition was defined at the outlet boundary. LBE with constant thermal–physical properties (corresponding Prandtl number is 0.025) was chosen as a working fluid. In the current study, four pitch-to-diameter ratios $P/D=1.1, 1.2, 1.3$, and $1.5$ were investigated. For each pitch-to-diameter ratio, RANS simulations were performed for bulk Reynolds numbers $R{e}_b=10000, 20000, 40000, 60000, 100000$, and $120000$, respectively. The corresponding bulk Peclet numbers $P{e}_b$ are $250, 500, 1000, 1500, 2500$ , and $3000$, respectively. The turbulent Prandtl numbers $P{r}_t$ for RANS simulations calculated with the new model are then $5.00, 3.08, 1.80, 1.57, 1.50$, and $1.50$, respectively.

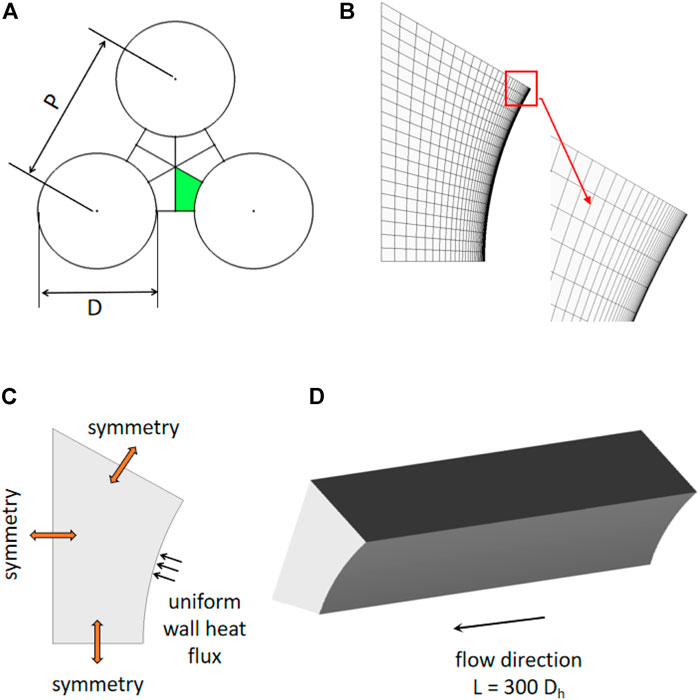
FIGURE 15. (A) Sketch of a bare rod bundle uniformly on the wall; (B) mesh used in the RANS simulations. (C) boundary conditions is the RNAS simulations; (D) sketch of the streamwise domain length.

Figures 16A–D compare, then, the bulk Nusselt number obtained by RANS simulations with that given by the experimental correlations Eqs. 25–27 for $P/D=1.1, 1.2, 1.3$, and $1.5$, respectively. It is shown as follows:

1) The same trend of the bulk Nusselt number$N{u}_b$ increasing with the bulk Peclet number $P{e}_b$ but decreasing with the $P/D$ ratio is predicted by all the three experimental correlations, as well as by the RANS simulations.

2) For the tight-spaced bundle of $P/D=1.1$, a large scattering exists among the experimental correlations. Although the values of $N{u}_b$ calculated with the correlation of Gräber and Rieger (1972) and Ushakov et al. (1977) are still comparable, they are both much higher than those predicted by the correlation of Mikityuk (2009). $N{u}_b$ obtained by the RANS approach with $P{r}_t=0.9$ is higher than that obtained by the RANS approach with the new model for $P{r}_t$. But they all lie within the range defined by the three experimental correlations.

3) However, the situation is much different for the loosely spaced rod bundle of $P/D$ ratio larger than 1.2. $N{u}_b$ predicted by the three correlations agrees well with each other. In general, for the loosely spaced rod bundle, the bulk Nusselt number obtained by the RANS approach with the conventional choice of $P{r}_t=0.9$ is much higher than that predicted by the experimental correlations. With the new proposed model for $P{r}_t$, however, a much better agreement with the experimental correlations was able to be achieved. Compared to the RANS simulations with the Kays model, RANS simulations with the new model proposed in this study show a comparable yet slightly better agreement with the three experimental correlations.

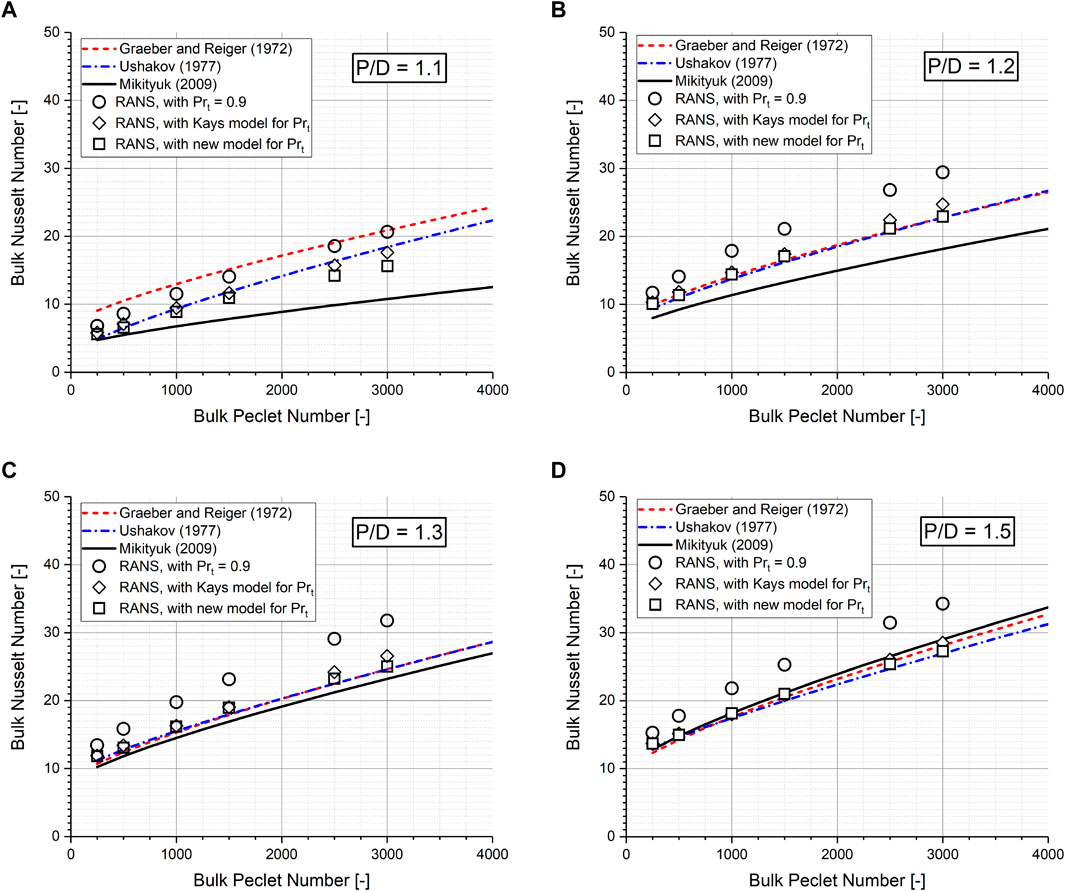
FIGURE 16. Validation of the proposed model on turbulent Prandtl number: bare rod bundle of P/D ratio equals (A) 1.1; (B) 1.2; (C) 1.3 and (D) 1.5.

5 Conclusion and outlook

In this study, LES/DNS simulation results of a fully developed forced turbulent channel flow up to $R{e}_{\tau }=2000$ at $Pr=0.01$ and $0.025$ were used as a reference, to which the RANS approach with the simple turbulent Prandtl number concept was compared and calibrated. Based on the calibrated relation with bulk Peclet number $P{e}_b$ , a new model for turbulent Prandtl number $P{r}_t$ used in the RANS approach was proposed and validated. The main conclusions derived are summarized as follows:

1) Heat transfer characteristics of the low-Prandtl number liquid metal depend strongly on the turbulent Prandtl number $P{r}_t$. An accurate estimation of $P{r}_t$ is of essential importance when applying the RANS approach to simulate the turbulent heat transfer of liquid metal. The conventional choice of $P{r}_t=0.9$ is proven to be not suitable for the liquid metal, with which the bulk Nusselt number $N{u}_b$ could be overestimated by up to 40%.

2) Taking the LES/DNS simulation results of the fully developed forced turbulent channel flow as a reference, the RANS approach with the turbulent Prandtl number concept was assessed. It was found that the optimum value of $P{r}_t$ used in the RANS approach for the low-Prandtl number liquid metal decreases with bulk Peclet Number $P{e}_b$ and tends to approach a constant value of 1.5 as $P{e}_b$ becomes larger than 2000.

3) Based on the aforementioned relation between $P{r}_t$ and $P{e}_b$, a new model expressing $P{r}_t$ solely in dependence on $P{e}_b$ was proposed in this study. Validation of the proposed model was carried out with available LES/DNS results of a local temperature profile in a concentric annulus and a loosely spaced bare rod bundle, as well as with experimental correlations on bulk Nusselt number $N{u}_b$ in a circular tube and bare rod bundle in a triangular arrangement. An overall good agreement of the RANS simulation results with the LES/DNS results, as well as with the experimental correlations was achieved, which demonstrates the adequacy of the proposed new model for $P{r}_t$ in this study.

4) To summarize, it could be concluded that the RANS approach with the simple concept of a constant global turbulent Prandtl number $P{r}_t$ is a suitable tool for simulating the forced convective turbulent heat transfer with the low-Prandtl number liquid metal, provided an appropriate $P{r}_t$ is specified. The RANS approach with the turbulent Prandtl number concept is, and will still be the only feasible approach when dealing with industrial application of turbulent heat transfer with the low-Prandtl number liquid metal. Therefore, it is believed that the model developed in the current study will have a promising perspective for engineering applications.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XH—writing–original draft preparation; methodology; investigation; data curation; visualization. BP—conceptualization; methodology; investigation; writing–original draft preparation; writing–review and editing; project administration; funding acquisition. XC—software; investigation; writing–review and editing YY—methodology; project administration; writing–review and editing.

Funding

This work was financially supported by the Natural Science Foundation of Guangdong Province (2021A1515010391).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References