Power optimization control of VSC-HVDC system for electromechanical oscillation suppression and grid frequency control

1 Introduction

With the continuous advancement of the low-carbon energy strategy in China, there are continuously increasing applications of large-scale generation of new energies, Liu et al. (2020); You et al. (2022), and the installed proportion of synchronous generators (SGs) has gradually decreased. The rotating reserve and inertia have been significantly reduced, the frequency fluctuations and electromechanical oscillations of the power grid frequently occur, posing a great threat and challenge to the safe and stable operation of the power grid. As a result, maintaining grid frequency stability and effectively suppressing electromechanical oscillations are critical issues, Kundur et al. (2004). Power electronics connected to the public grid must actively participate in frequency control and oscillation suppression, Xu and Wang (2021).

Existing solutions mainly include: 1) The power system stabilizer to compensate for the negative damping, Kumar (2016); 2) The installation of synchronous condensers to improve the inertia level and damping ability of the power system to suppress electromechanical oscillations and frequency fluctuations, Nguyen et al. (2019); 3) The use of reactive power compensation devices such as the static synchronous compensator to regulate the reactive power output and change the voltage level and power flow distribution of the system, thereby suppressing the grid electromechanical oscillations, Li et al. (2020); 4) The use of energy storage devices to quickly emit or absorb active and reactive power to maintain the active power balance in the system and suppress power oscillations, yet energy storage devices are more expensive and difficult to apply on a large scale, Zhu et al. (2019); 5) The use of the power of the new energies such as photovoltaic and wind generations to compensate for the power deficits or surpluses in the power system Yang et al. (2021), but new energy generations typically operate in the maximum power point tracking mode; if used for grid frequency control and electromechanical oscillation suppression, a certain amount of capacity must be reserved for active participation in the regulation of the system dynamic process at any time, which will sacrifice their inherent power generation capacity, Li et al. (2020).

Currently, the voltage source converter (VSC) based high-voltage DC (HVDC) transmission system is one of the best solutions for large-scale renewable energy exploiting, and has been widely applied in practical projects such as grid-connected wind farms, weak grid power transmission, and islanding power supply, Zhang et al. (2011); Lee et al. (2018). As the VSC-HVDC system has the advantage of fast and independent control of active and reactive power, and it does not require reactive power compensation from the AC grid, it has attracted a lot of attention for suppressing electromechanical oscillations and maintaining power system frequency stability, Wang et al. (2019); Xiong et al. (2021b). Sun et al. (2021) states that when the VSC-HVDC system uses a constant power control strategy, the damping level of the power system cannot be increased. For this reason, the VSC-HVDC system should operate in the variable power control mode to inject real-time adjustable active or reactive power into the SG network based on the change of the grid state, in order to enhance the suppression of electromechanical and frequency oscillations by the VSC-HVDC system. In addition, Varma and Maleki (2019) points out that when the VSC absorbs or emits reactive power to change its voltage at the integration point and improve the grid power distribution, it functions as a STATCOM that can quickly and smoothly modulate the reactive power without the need for a large amount of reactive power provided by the grid Xiong et al. (2015).

To realize that HVDC actively participates in the frequency control and suppresses electromechanical oscillations, the VSC control needs to be improved, such as by adding droop control, inertia control, and proportional-derivative (PD) control, Peng et al. (2020); Shi et al. (2021). Droop control and inertia control cannot adjust the magnitude and speed of frequency change at the same time, Xiong et al. (2022); Wang et al. (2015); the PD control necessitates high precision on system parameters, and the expected control performance is difficult to achieve, Li et al. (2020); Ling et al. (2021). Accordingly, Fang et al. (2018) improved the original virtual inertia control, and proposed a virtual SG (VSG) control with characteristics similar to SGs. To suppress the inherent power oscillation problem of the VSG control and improve the frequency response speed, Kerdphol et al. (2019) proposed an improved VSG strategy based on the fuzzy logic algorithm. However, various improved VSG strategies require information on grid inertia and damping parameters to obtain the optimal inertia and damping control parameters, Ali et al. (2019). To this end, Xiong et al. (2021a) developed a frequency trajectory planning control that decouples from the grid’s disturbances and inertia/damping information that cannot be obtained.

All the previously discussed schemes make the VSC provide appropriate power support as soon as possible to recover the power balance. Obviously, when the frequency and the rotor oscillation exceed their limits, the adjustment power will also exceed the operating range that VSC can withstand. At this time, the VSC over-voltage and -current protection will be triggered, and the additional control mentioned above will lose its intended functionality. Therefore, the VSC control to suppress the frequency fluctuation and electromechanical oscillation must consider the limited VSC control capability under large disturbances. To this end, a coordination control for the VSC-HVDC active/reactive power, based on the Rapid Power Compensation (RPC) mode, is proposed to suppress the electromechanical oscillation and frequency fluctuation, and enhance the safe and stable operation of the power grid under large disturbances. Finally, the effectiveness and superiority of the proposed work are verified by various simulation results.

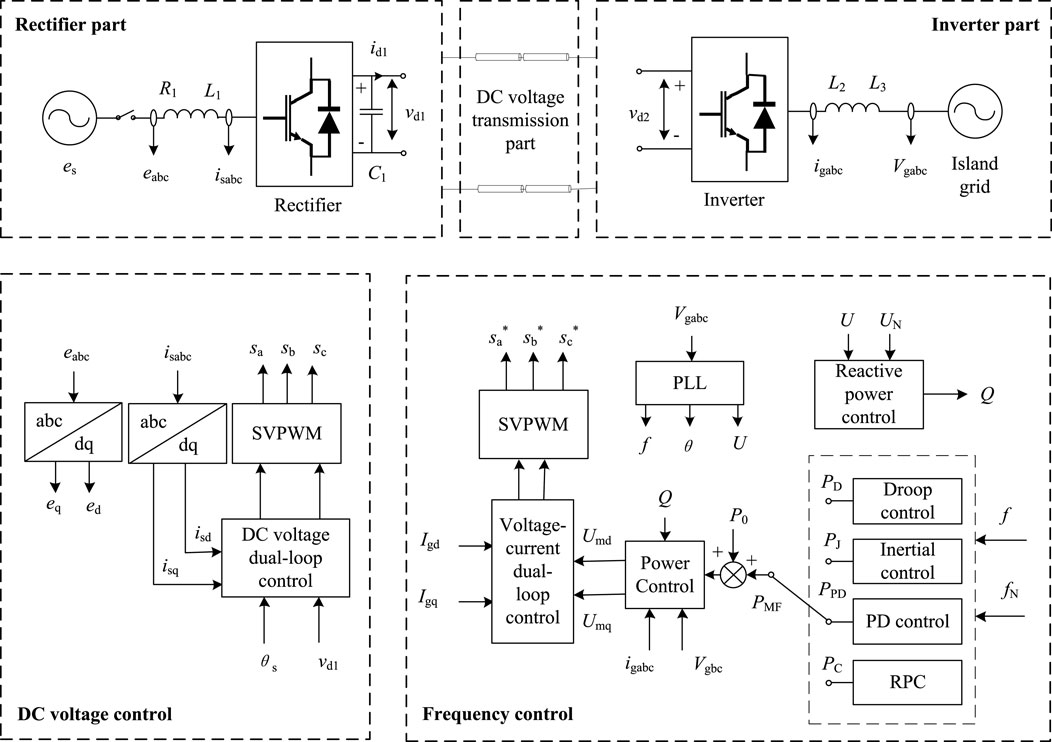
2 VSC-HVDC system structure and its control strategy

The basic structure of the VSC-HVDC is shown in Figure 1 e_abc and i_sabc are the voltage and line current at the sending-end grid, respectively; θs is the grid voltage phase angle; v_d1 and v_d2 are the DC voltages at the rectifier end and the inverter end, respectively; i_d is the DC line current; V_gabc and i_gabc are the voltage and current at the receiving-end grid, respectively, and U_N and f_N are the rated voltage and frequency, respectively; P_D, P_J, P_PD, and P_C are the regulated power provided by the droop control, the inertia control, the PD control, and the RPC control, respectively; P₀ and Q are the steady-state active- and reactive- power provided by VSC-HVDC to the receiving-end grid, respectively. Through the phase-locked loop, Liu et al. (2022a); Liu et al. (2022b), V_gabc provides the frequency f, phase θ, and voltage amplitude U at the receiving-end grid, and

FIGURE 1. The VSC-HVDC system structure and its converter control structure.

At the sending end, the reactance L₁ of the rectifier limits the rise of the short-circuit current; the capacitor C₁ suppresses the DC voltage fluctuation. The VSC-HVDC system usually adopts a constant DC voltage control to effectively maintain the DC voltage stability; the inner loop tracks the VSC current change in real time, and the outer loop controls power and voltage. When the grid voltage is stable, by neglecting the power loss of the VSC itself, we have

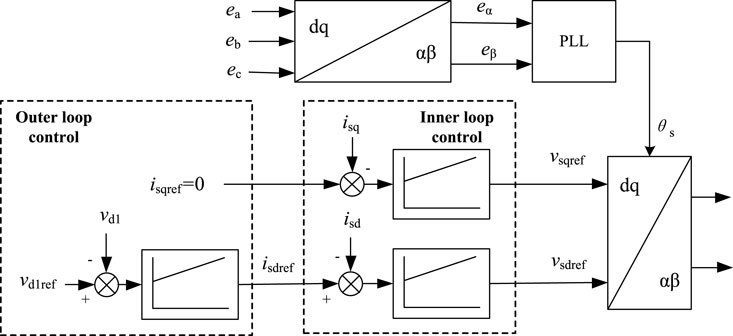
Both v_d1 and P are proportional to the d-axis component i_sd of the rectifier output current, according to which the control rule of the sending-end VSC can be obtained, as shown in Figure 2, where the active and the reactive power are decoupled and controlled separately. If the reactive power reference of the sending end VSC is set to 0, the inner loop can realize steady-state-error-free control to i_sd and i_sq Xie et al. (2014). In addition, since the rectifier realizes the DC voltage regulation, the VSC of the receiving-end grid only needs to track the dispatch instructions of the local grid; at the same time, it can be designed to additionally suppress the electromechanical oscillations and frequency fluctuations of the receiving-end grid.

FIGURE 2. Control strategy of the sending-end converter of the VSC-HVDC system.

3 VSC-HVDC suppressing electromechanical oscillations and frequency fluctuations of receiving-end grid

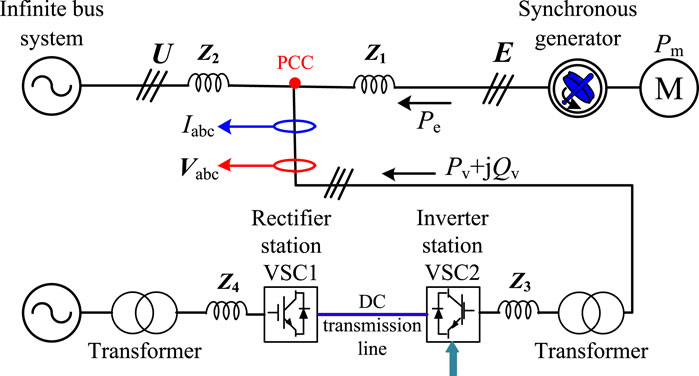
To analyze the principle and strategy of the VSC-HVDC to suppress the electromechanical oscillations and frequency fluctuations of the receiving-end grid, this paper uses an equivalent SG to represent the receiving-end grid, as shown in Figure 3. In addition, to simulate the electromechanical oscillations of the rotor speed of the SG around the rated speed, the equivalent SG is operated in parallel with an infinite bus, so that the SG rotor speed is always clamped around the rated value. When it is necessary to simulate the frequency fluctuation where the frequency deviates from the rated frequency, the infinite bus system can be disconnected. With reference to Figure 3, P_m is the mechanical input power of the prime mover, P_e is the SG electromagnetic power, and P_v and Q_v are the active- and reactive- power injected into the SG network by the VSC-HVDC. I_abc and V_abc are the current and voltage at the point of common coupling (PCC). U is the voltage between system two and the PCC, and E is the voltage between the SG and the PCC. Z₁, Z₂, Z₃, and Z₄ are equivalent impedances of corresponding lines.

FIGURE 3. Integration of the HVDC into the system with oscillations and frequency fluctuations.

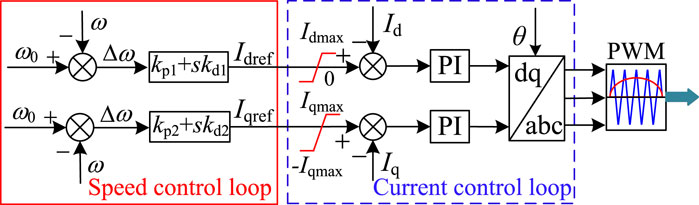
When suppressing the electromechanical oscillations and frequency fluctuations, the inverter VSC2 of HVDC usually adds the damping and the inertia control on top of the direct current control in Figure 4, where I_d is the measured current and I_q is the measured reactive current; I_dref and I_qref are the reference values of active and reactive currents, respectively. ω₀ and ω denote the rated and detected values of rotor speed of the SG (oscillation suppression mode) or grid angular frequency (frequency control mode), respectively; k_p1, k_p2, k_d1, and k_d2 are gains of the P and D controllers corresponding to the active and reactive control loops, respectively.

FIGURE 4. Control strategy of the VSC-HVDC to suppress oscillations and frequency fluctuations.

As can be seen from Figure 4, after coupling I_dref and I_qref with the rotor speed (grid frequency), the power output of the VSC-HVDC system can be modulated quickly and independently, by controlling the reference values of active and reactive DC current components separately (on the d and q axes in the dq coordinate system), injecting controllable active and reactive power into the receiving-end network and improving the damping capacity and inertia effect of the system. The relevant principles and analysis can be found in Li et al. (2020).

Chi et al. (2019) points out that the damping control is based on the P controller to achieve power modulation, which helps to improve the damping capability of the system, and the inertia control is implemented with the help of the D controller to improve the system inertia. Also, the above strategies are conventional controls for grid-connected inverters to suppress electromechanical oscillations. Through the PI controller, I_d and I_q can track their references, I_dref and I_qref (Chi et al., 2019), and thus quickly and effectively regulate the active- and reactive- power from the VSC, finally realizing the suppression of electromechanical oscillations and frequency fluctuations of the receiving-end grid, and reducing the fluctuation range of the rotor speed and the grid frequency.

Based on the linearized model in Li et al. (2020), when the active- and reactive- power of the VSC-HVDC system are injected into the infinite system, the inertia coefficient T_J and the damping coefficient T_D of the power system can be obtained respectively as

where D and H are the damping and inertia inherent to the power system; β and μ are the VSC2 control coefficients for active and reactive controls, respectively.

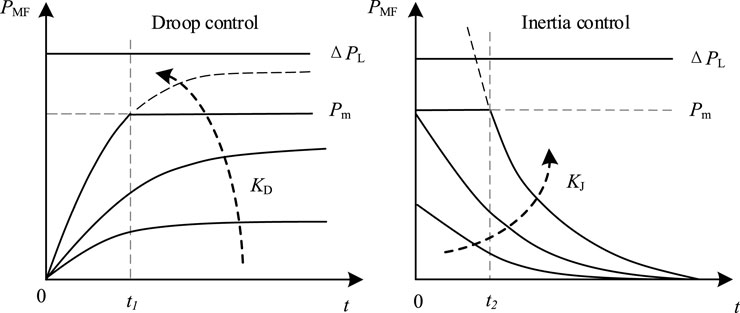
Obviously, the larger k_d1 and k_d2 are, the larger T_J is, the stronger the inertia provided to the grid, which can effectively suppress the rate of change of speed/frequency dω/dt; the larger k_p1 and k_p2 are, the larger T_D is, which can effectively suppress the speed/frequency deviation Δω. However, when the grid suffers from a large disturbance resulting in a large dω/dt and Δω, to effectively suppress the power unbalance, a large range of power variations is required to be output by VSC (i.e., the PD controller gain should be increased), which may exceed the VSC2 design capacity S and power transmission limits shown in Figure 5.

FIGURE 5. VSC power variation law under two typical control strategies.

If the current control dynamic in Figure 4 is ignored, the regulation power of the VSC in the receiving-end grid under the damping control, the inertia control, and the PD control can be roughly expressed as:

where K_D is the damping control coefficient, K_J is the inertia control coefficient, and K_p and K_d are the proportional and differential coefficients of the PD controller, respectively.

Obviously, if the gains of the damping control, the inertia control, and the PD controller are reduced, the VSC regulation power can be reduced to prevent VSC overload protection, but at the same time, the inertia and damping of the power system at the receiving end will also be weakened. For this reason, the influence law of the PD controller gains on VSC power output is analyzed in this paper.

4 RPC mode of VSC-HVDC system

Assume that I_m characterizes the maximum current of the VSC; I_d max and P_max are the I_d limit and power transmission limit, respectively. Since VSC2 cannot absorb active power, the power and current values P_v, Q_v, I_d, and I_q shown in Figure 3 and Figure 4 satisfy the following constraints

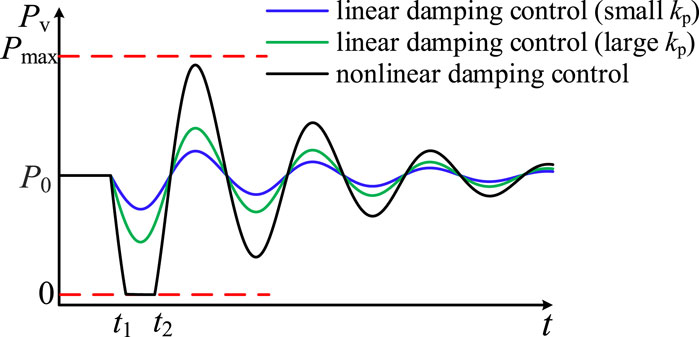
With reference to Figure 6, where the HVDC operates with the damping control as an example, if k_p is increased, the VSC active power will also gradually increase (with P₀ being the steady-state output value of the VSC active power), and the VSC will operate in linear damping control and non-linear damping control modes, respectively. Among them, the non-linear control is caused when k_p is amplified to a certain degree. When the rotor speed/grid frequency is greater than the rated value, the VSC active output value will be 0, as shown in Figure 6 for t₁–t₂; conversely, the VSC will output active power at the limit value P_max.

FIGURE 6. VSC active power output under different P controller gains.

Similarly, when the gain of D controller k_d increases to a certain degree, the VSC will output active power at a constant value of 0 or P_max for a specific period of time (i.e., the non-linear inertia control is used), and the controller will not be able to adjust the output power of the VSC.

The non-linear control is caused when the damping and inertia support of the HVDC are enhanced to a certain degree, and the ability of the non-linear control to suppress electromechanical oscillations and grid frequency fluctuations is also better than the damping and inertia control (Chi et al., 2019). Therefore, when k_p1, k_p2, k_d1, and k_d2 in the speed/frequency control are amplified to the limit, depending on the positive and negative polarity of the deviation, the power output of VSC2 in the full time range is:

1. Delivering constant active power alternately, using the active limit power P_max of the inverter station VSC2 or 0 as the output reference;

2. Continuously absorbing or emitting constant reactive power with the remaining capacity of the inverter station as the limit value.

In this paper, the operation mode with the above two conditions of alternating constant power is referred to as the RPC mode of the VSC-HVDC system, which can maximize the suppression of grid electromechanical oscillations and frequency deviations. The theoretical analysis is shown as follows.

If the grid is under steady-state condition, then P_m and P_e are equal and the system power balance is met; if the grid load increases suddenly and the power change is ΔP_m, a power shortage will occur, resulting in a continuous reduction in rotor speed/grid frequency (Δω = ω₀−ω > 0). Therefore, the VSC-HVDC system should increase the active output or absorb reactive power to suppress the deceleration energy of the SG rotor and grid frequency.

If the VSC-HVDC system increases the active power by ΔP_e, which yields 0 < ΔP_e < ΔP_m, the SG swing equation and the grid frequency response can be described as

As an example, if the VSC-HVDC system operates in the RPC control mode to regulate only the active power, then ΔP_e = P_max−P₀. According to Eq. 9, we have

For VSC-HVDC to operate with the inertia control, the corresponding VSC active power should satisfy

Considering that at the starting moment when the power system suffers from electromechanical oscillations/grid frequency fluctuations (t = 0), |dω/dt| is its corresponding maximum value, while the VSC-HVDC has not yet generated additional active power to suppress the unbalanced active power of the system under the action of the control strategy, i.e., ΔP_e = 0; at this time, |dω/dt|_max is

If the VSC-HVDC is made to operate with the linear inertia control, the maximum D controller gain is

Eq. 9 and Eq. 13 show that: after the HVDC provides inertia to the grid using the inertia control (with the gain taking its maximum value), the rotor swing equation/grid frequency response equation can be described as

From Eq. 14, the value of |dω/dt| at this point is

Obviously, from the comparison of |dω/dt| shown in Eq. 10 and Eq. 15, it follows that

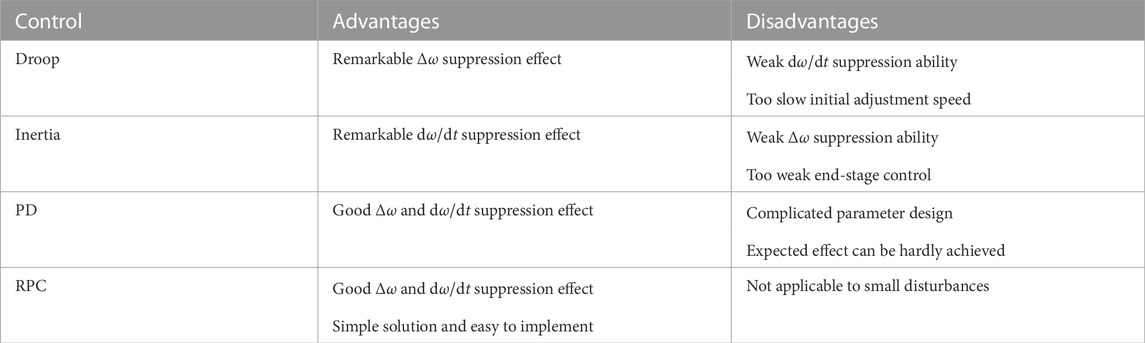
The comparison results of the rate of change of SG rotor speed and grid frequency under different control strategies [see Eq. 16] show that: in the case of the same maximum available VSC capacity, the suppression ability of the VSC-HVDC system based on the RPC control mode for dω/dt is significantly stronger than that of the linear inertia control strategy; similarly, the suppression ability of the VSC-HVDC system based on the RPC control mode for the speed/frequency deviation Δω is stronger than that of the conventional damping control strategy. The essential reason for the best regulation performance of the RPC strategy is that its supporting power to the receiving end grid can reach the maximum power output by the VSC. It should be noted that under the optimal control parameters, the oscillation suppression effect and grid frequency control effect of the PD control are equivalent to those of the RPC control, but the optimal PD control parameters are difficult to obtain. In contrast, the RPC control not only quickly compensates for the power shortage of the receiving end grid, but also avoids the problems of grid parameter measurement and controller parameter optimization. Table 1 summarizes the comparison of advantages and disadvantages between the RPC control strategy and the conventional control strategy.

TABLE 1. Comparison of advantages and disadvantages between typical control strategies.

5 RPC based strategy for electromechanical oscillation suppression and frequency control

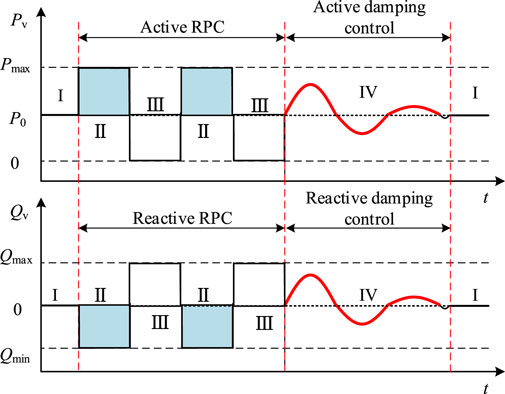
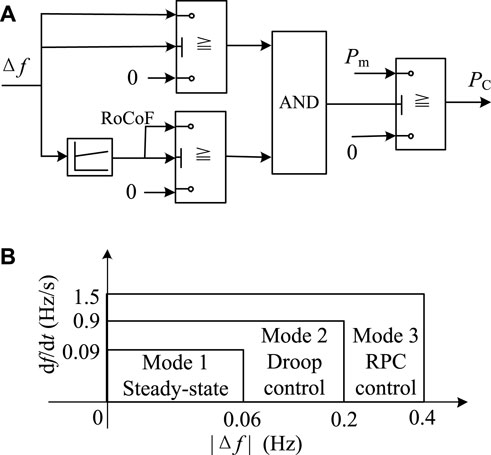
Based on the above analysis and conclusions, this paper integrates the respective advantages of the RPC mode and the damping control strategy, and proposes a coordinated active/reactive power control for the VSC-HVDC system to suppress grid oscillations and frequency fluctuations. With reference to Figure 7, the basic control and switching principles are:

1. If dω/dt and Δω are large, the VSC-HVDC system should switch to the RPC mode, to quickly compensate for system power shortage or suppress system excess power, and efficiently suppress Δω, dω/dt, and other speed indicators to avoid triggering the related relay protection devices of the power system. Under this mode, the VSC output active- and reactive- power should be switched to

2. When dω/dt and Δω meet the requirements, an additional damping control makes the VSC-HVDC system exit the RPC mode and gradually return to the power delivery mode, and continue to provide damping torque to reduce the oscillation area of the SG rotor and grid frequency.

FIGURE 7. VSC-HVDC system power output under RPC mode.

The switching conditions and power commands corresponding to different conditions are discussed below. In the following discussion, ω_d, ω_th, and R_th are the thresholds of |Δω| and |dω/dt|, respectively, and 0 < ω_d < ω_th and R_th > 0. ω_d is the |Δω| threshold for VSC switching to the damping control, ω_th is the |Δω| threshold for VSC entering the RPC mode, and R_th is the |dω/dt| threshold for VSC switching to the RPC mode.

1. Condition I: When dω/dt and Δω are within the safety interval, i.e.,

the system is in steady state or the oscillations/fluctuations have been suppressed and the VSC should operate in steady-state transmission mode without adjusting its power output, i.e., P = P₀, and Q = 0.

2. Condition II: If dω/dt and Δω simultaneously satisfy

then there is a serious power deficit in the grid, VSC-HVDC should increase the active power in time to compensate for this power deficit. I_d should be immediately increased to I_dmax, to provide continuous positive and fast active power compensation to the grid. At this time, P = P_max to significantly suppress Δω and dω/dt. The remaining capacity of the inverter is used to absorb the grid reactive power to the maximum extent, regulate the PCC voltage, reduce the SG output power, and suppress the power angle increase. The reactive current I_q and Q commands are

3. Condition III: If dω/dt and Δω simultaneously satisfy

then there is a power surplus in the system. The VSC-HVDC system should immediately minimize the active output, i.e., I_d should be immediately reduced to 0 in reverse, so that the active output P of the VSC-HVDC system is 0, while all the remaining capacity of the inverter station VSC2 will be used to transmit reactive power to the system, increasing the electromagnetic power of the SG, and providing reverse fast power compensation to the grid to suppress the active power surplus of the power system. At this time, the reactive current command of the current loop is set to I_q = −I_m, and the reactive power of the inverter station is Q = S.

4. Condition IV: If the rotor speed indexes dω/dt and Δω satisfy

then the SG has a slight rotor oscillation phenomenon or a small range of grid frequency fluctuation. In order to ensure that the VSC-HVDC system delivers active power as much as possible, it should gradually return to the steady-state generation mode and switch to the damping control strategy of active/reactive power coordination to provide the necessary damping torque to the grid, suppressing the electromechanical oscillations and grid frequency fluctuations as much as possible and improving the frequency quality of the SG network. At this time, the active- and reactive- power at the inverter side of the VSC-HVDC system are set to be

When HVDC uses the RPC control to suppress large frequency fluctuations of the receiving-end grid caused by large disturbances, the relevant thresholds must strictly comply with the grid frequency indexes defined by the grid code, i.e., the frequency deviation Δf or the rate of change of frequency (RoCoF) df/dt. For example, GB/T 33593–2017, the grid integration standard for distributed energy sources in China, stipulates that the frequency deviation |Δf| shall not exceed 0.2 Hz during continuous operation, and shall not exceed 0.5 Hz when the relay action terminates power transmission. To ensure that the power grid can meet the above frequency index requirements under various disturbances, a necessary margin must be reserved for the HVDC system when it suppresses frequency fluctuations. Accordingly, the RPC based frequency control will be implemented according to Figure 8, where P_C = P_m < ΔP_L; if Δf or df/dt reaches the action threshold of the RPC control, the VSC power command is directly set to the maximum power capacity P_m. Similarly, when the grid frequency indexes decrease to the designed threshold, the VSC control mode switches to the damping control mode (i.e., droop control); when the grid frequency returns to the rated value, the VSC resumes the conventional constant power control mode. With reference to Figure 8, the three modes are autonomously switched according to the detected frequency of the receiving-end grid, to enhance the frequency fluctuation suppression effect and ensure the frequency stability of the receiving-end grid.

FIGURE 8. VSC frequency control based on RPC mode. (A) Control diagram. (B) Working mode switching.

Obviously, when electromechanical oscillations or frequency fluctuations occur in the sending-end grid, the rectifier can also adopt a similar method to make the VSC-HVDC system actively suppress the electromechanical oscillation process or frequency fluctuation problem in the sending-end grid.

6 Simulation verification

In this paper, the MATLAB/Simulink platform is used to compare and verify the suppression capability of the VSC-HVDC system against grid electromechanical oscillations and frequency fluctuations, when the RPC mode is combined with the damping control strategy. The simulation topology is shown in Figure 4.

6.1 Electromechanical oscillation suppression

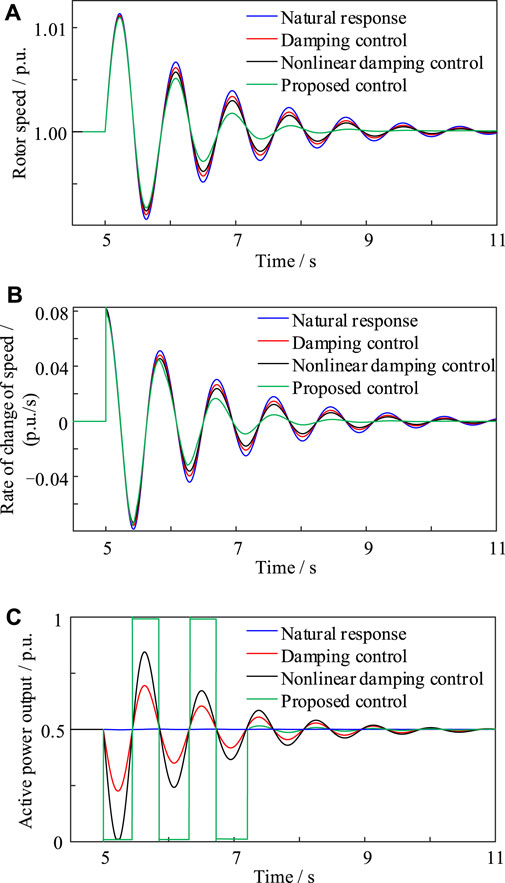
The mechanical power of the prime mover of the receiving end grid changes abruptly at 5 s, causing an electromechanical oscillation. The VSC is made to operate in the absence of power control (k_p = 0), and in the presence of conventional damping control (k_p = 300) and non-linear damping control (k_p = 700) by adjusting the P controller gain. The SG rotor speed under the above control strategies is compared with the coordination strategy proposed in this paper, and the simulation results are shown in Figure 9.

FIGURE 9. Oscillation suppression. (A) Rotor speed. (B) Rate of change of speed. (C) HVDC power.

As shown in Figures 9A,B, compared with the working condition of the VSC-HVDC system without power control (i.e., k_p = 0), the electromechanical oscillation amplitude and the oscillation amplitude of SG rotor speed gradually decrease as the parameter k_p increases. However, the rotor oscillation period does not change, indicating an almost unchanged inertia level despite the fact that the grid damping capability is enhanced. The corresponding active power output waveforms of the inverter station VSC2 under different control strategies are given in Figure 9C. Note that in this case Δω is small when switching to the damping control strategy to modulate the power output, and therefore k_p can be appropriately amplified (here the value is taken as 1,000).

It can be concluded that the linear damping control strategy is not conducive to enhancing the ability of the VSC-HVDC to suppress the grid electromechanical oscillation. When the coordinated suppression strategy proposed in this paper is adopted, the SG rotor recovers to its rated speed significantly faster, and the amplitude of rotor oscillation is significantly reduced. At the same time, the rotor speed variation rate dω/dt is substantially suppressed. This indicates that the oscillation suppression effect of the proposed strategy is stronger than that of the damping control and the local RPC strategy.

6.2 Frequency fluctuation suppression

In this simulation scenario, the infinite bus in Figure 3 is removed to simulate the capacity-limited receiving end grid. To simulate the operating condition where the power grid is subject to small disturbances, a disturbance of 0.1 p.u. Is suddenly added to the receiving end power grid at t = 30 s, when the droop control starts frequency control (see Figure 10). Under the condition of small disturbance, the frequency deviation using the droop control is reduced by 0.09 Hz compared with the natural response, the maximum value of the rate of change of frequency (RoCoF) is 0.14 Hz/s smaller than that of the natural response, and the compensation power to the receiving-end grid is significantly increased. It can be seen that the suppression effect of the droop control on frequency deviation is more prominent than that of RoCoF. At this time, the frequency is within the allowable range of the system during steady-state operation, and the HVDC system can smoothly exit the droop control mode.

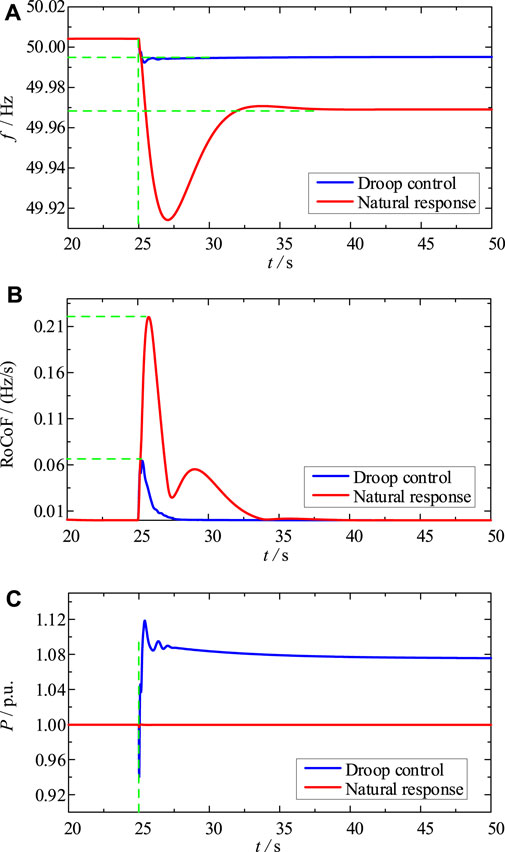
FIGURE 10. Frequency control under small disturbance. (A) Grid frequency. (B) RoCoF. (C) Inverter power.

To simulate the large disturbance, a disturbance of 0.9 p.u. Is suddenly added to the receiving end grid at t = 25 s (see Figure 11). The simulation results show that: with the proposed strategy, the HVDC system can adjust the operation mode autonomously, and quickly compensate for the power shortage of the receiving-end grid; the frequency of the receiving-end system is stabilized to 49.96 Hz within 3 s, and the maximum RoCoF is only 0.15 Hz/s. Conversely, under the same interference condition, the frequency control capability of the droop control is extremely limited. Obviously, the RPC control has a strong suppression effect on both frequency deviation and RoCoF.

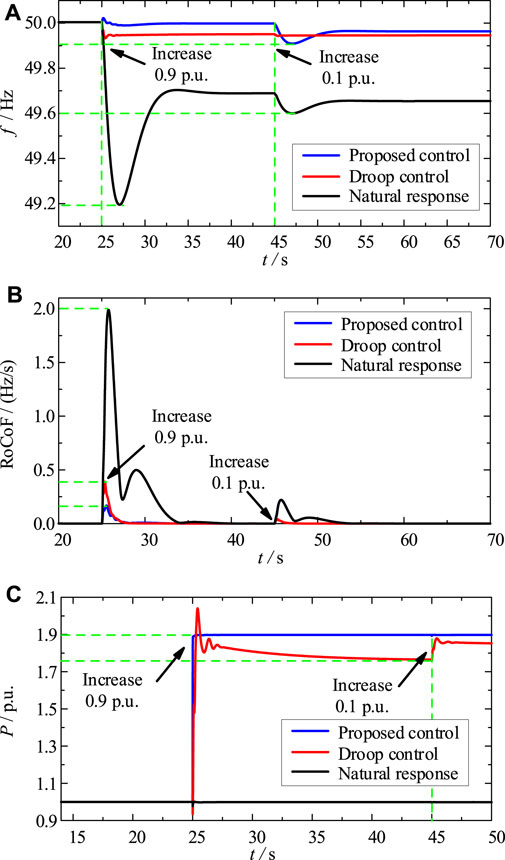
FIGURE 11. Frequency control under hybrid disturbance. (A) Grid frequency. (B) RoCoF. (C) Inverter power.

The adaptive performance of the proposed HVDC control is further tested by adding a disturbance of 0.1 p.u. at t = 45 s. The test results (see Figure 11) show that the proposed control strategy can ensure that the HVDC system can autonomously sense the frequency change trend of the receiving end grid under different disturbance conditions, adjust the inverter operation mode, and continuously and dynamically match the real-time operating condition of the receiving-end power grid to always effectively suppress its frequency fluctuation problem.

7 Conclusion

Under the VSC capacity constraints, this paper compares the suppression level of rotor speed and frequency change rate for HVDC operating in the RPC mode and with the linear control. HVDC operating in the RPC mode has significantly suppression ability of electromechanical oscillations and frequency fluctuations. Then, this paper integrates the RPC mode and the damping control, and designs four operating conditions and power commands to regulate the HVDC power. The proposed active/reactive power coordination strategy, based on the RPC mode, can quickly suppress the system power imbalance and significantly improve the suppression effect of the HVDC on electromechanical oscillations and frequency fluctuations. Simulation results show that the supporting power introduced by the conventional control and its response speed are much smaller than the shortage power required when the grid is disturbed. Conversely, the RPC control can fully utilize the VSC power reserve, quickly and sufficiently compensating for the lack power, stabilizing the grid frequency in time and effectively suppressing the electromechanical oscillation.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

All the authors conceived and designed the study. CB, JW, and YQ performed the simulation. CB, JW, and XL conceived and designed the simulations. YQ and JX wrote the manuscript with the guidance from JS and FL.

Conflict of interest

CB, JW, XL, JX, and FL were empolyed by Guangzhou Power Supply Bureau, Guangdong Power Grid Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References