More Environmental Sustainability Routing and Energy Management for All Electric Ships

Introduction

Background And Motivation

The global shipping industry has produced about 1 billion tons of greenhouse gas emissions per year from 2007 to 2018, acting as a major player in the global carbon emission, and it is estimated that if no actions are taken, the global greenhouse gas emission would triple by 2050 compared to 2007 (International Maritime Organization, 2015). All electric ships (AESs), which refer to the full electrification of the propulsion system of ships, have been recognized as an efficient tool due to their high efficiency and low pollution. The study of AES is generally categorized into two directions: planning and energy management strategies. The optimal routing of AESs is a typical procedure to reduce both carbon emissions and operation cost (Liu and Shang, 2017), and along the routing, the proper management of AESs among electricity and fuels, as the combination of diesel generators (DGs), energy storage systems (ESSs), fuel cells (FCs), photovoltaic (PV), and cold ironing, can further reduce the emissions significantly (Skjong et al., 2016). Thus, it is of great importance to harmonize a joint voyage planning and energy management scheduling to create a more environmentally friendly marine transportation industry.

Literature Review

Currently, the planning and design of AES has gained more attention, aiming to reduce the cost of operation and transportation, where the key studies consist of the ship voyage routing problem and the design of energy storage systems (ESS). Agra et al. (2013) proposes a routing plan of vessels considering the loading/unloading operation and fuel consumption rate. The routing of the fuel supply vessel is addressed as a rich multi-trip vehicle routing problem while minimizing the voyage costs in Christiansen et al. (2017), and fuel management and carbon emission evaluation are added in De et al. (2020) for maintaining the service level of ports along the route. The speed optimization model (Fan et al., 2019), different shipping operations (De et al., 2019), and dynamic environments with both spatial and temporal uncertainties (Sidoti et al., 2017) are considered in the route-planning problem, respectively. However, the above studies fail to combine power generation scheduling with routing problems, resulting in incomplete planning outcomes.

In addition to the ship voyage routing planning, the design of onboard ESS is also critical in view of fuel consumption depletion and emission mitigation. It is proved that the optimized design of ESS can considerately improve system efficiency and economic performance (Sinsley et al., 2020). Since the high capital cost is a main drawback to deploy in AES, the sizing problem of ESS has been discussed in many works. The effects of ESS capacity planning are researched to obtain different targets, such as saving fuel cost (Kim et al., 2015), solving uncertainties of renewable energy (Yao et al., 2018), or mitigating voltage fluctuations (Elsayed et al., 2016). The sizing problem is further studied to reduce the greenhouse gas emission considering the swinging effect of a hybrid shipboard power system (Wen et al., 2016). Nevertheless, the voyage routine is decided as known information in those studies, and it is inadequate to only consider the ESS sizing problem faced with the higher requirements of maritime transportation.

Along with the above planning and design study of AES, the energy management strategy has also drawn a lot of research efforts. The energy management strategies can be separated as generation side management, load side management, and energy-storage side management. On the generation side, differential evolution (DE) (Yang et al., 2018) and non-dominated sorting genetic algorithm (NSGA-II) (Shang et al., 2016) are utilized to optimize the dispatch of power distribution to stabilize ship speed with respect to the corresponding propulsion curve. In Wu and Xia (2018), the cold-ironing technology, which establishes the electrical connections between seaports and ships, is used to provide services for the berthed ships in place of the master-slave generators. To further reduce air pollution, different types of FCs are employed as energy sources in AESs (Han et al., 2012), and a zero-emission hybrid FC ship is designed in Letafat et al. (2020). The impact of radiation time and geographical changes (Yao et al., 2018) on the uncertainty of solar energy is discussed for the uncertainty modeling of AES. As for the load side management, the dynamic programming (DP) algorithm (Kanellos et al., 2014) and an improved nested EMS (Lai and Illindala, 2018) are utilized to realize the optimal propulsion adjustment in the operation of AES. Furthermore, thermal load, combined cooling heating, and power unit and heat storage are considered in Li et al. (2020a) and Huang et al. (2020), respectively, to achieve a flexible multi-energy ship (MES) microgrid. In addition, the airborne power load and outdoor temperature are discussed in (Li et al., 2020b) to achieve the robust coordination of hybrid-MES. The energy-storage side management is concentrated to further reduce the fuel loss and improve the ship efficiency in Kanellos (2014), Fang et al. (2019), and Lai and Illindala (2021). A hybrid-ESS management with the consideration of the secondary downgrade cost is designed to prolong the lifetime of ESS (Fang et al., 2019) since those devices always experience frequent discharge or charge actions due to sudden load changes during sailing. A distributed cloud ESS is in zonal configuration to minimize the total cost and enhance the resilience of AES in (Lai and Illindala, 2021). Nevertheless, the voyage route is predefined in those studies, where the navigation routing problem is completely neglected.

Several researchers have studied the joint navigation routing and energy management scheduling problems aiming at reducing the voyage cost along the route. A coordinated optimal voyage and energy management of AES with the consideration of hybrid-ESS and sea states is proposed in (Hein et al., 2021). However, this study neglects the greenhouse gas emission completely, which is insufficient for the energy management of different ships in practice, and the routing problem of AES is only limited to three ports instead of an actual route of ship. Wen et al. concentrate on the uncertainty of photovoltaic power and electricity price of various harbors (Wen et al., 2020; Wen et al., 2021) along with voyage scheduling and energy management. However, the high capital cost of ESS should not be overlooked, and the potential of hydrogen has not been considered in the previous joint problem formulation, which leads to a less environmentally friendly management strategy. Several research works have been reported recently to achieve zero-emission with fuel-cell based hybrid energy system. The feasibility assessment has been conducted to demonstrate its effectiveness in Rafiei et al. (2021) and Ahmadi et al. (2021). In these works, the design is limited to the small ferry boat while the power capacity of the fuel cell is still limited.

Contribution and Paper Organization

This paper proposes a novel joint routing and energy management strategy with the consideration of both navigation routing and hybrid-ESS planning, via using hybrid fuels, e.g. diesel, hydrogen, solar, and cold ironing. A multi-objective optimization problem is formulated aiming at minimizing the investment cost, operation cost, and greenhouse gas emissions under photovoltaic uncertainties, which is reformulated as a bi-level tri-objective optimization problem. The upper level is designed for the variables related to the navigation routing and planning of ESS, which is solved through multi-objective optimization differential evolution algorithm (MODEA); the lower level is constructed for the power generation scheduling, which is solved by commercial tools such as GUROBI. The main contributions of this paper can be summarized as follows:

1) The navigation routing problem of all-electric ship with hybrid fuels is formulated as a bi-level tri-objective distributionally robust optimization problem to minimize the investment, operation and emission cost jointly, where the photovoltaic along the routine is depicted by a discrete ambiguity set.

2) A bi-level multi-objective optimization method is proposed, where a multi-objective differential evolution algorithm is used to design navigation parameters, battery ESS capacity, FCs, and weight between operation cost and emissions in the upper level, and energy management problem is solved through commercial tools in the lower level.

The rest of paper is organized as follows: Problem formulation introduces the architecture of maritime power system and formulates the mathematical model of main equipment and navigation routine planning. Proposed solution approach proposes a bi-level optimization method to solve the complex problem, and six case studies and one sensitivity analysis are conducted to test the feasibility and effectiveness of proposed method in Simulation Results. Finally, the conclusion and future work are presented in Conclusion.

Problem formulation

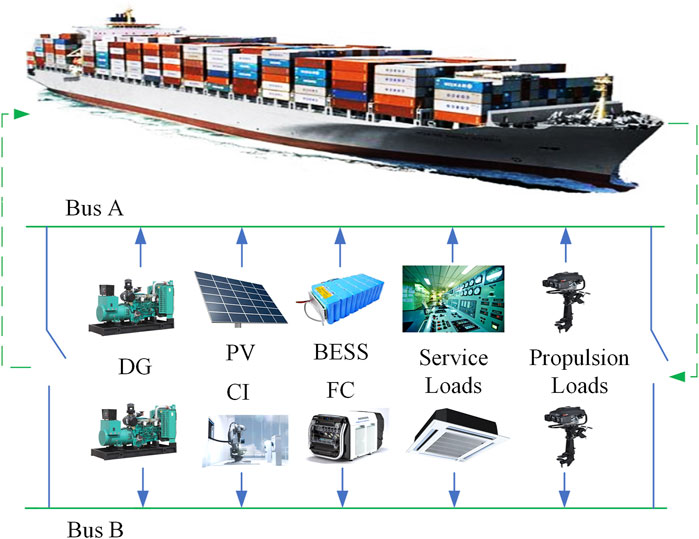
In this section, the maritime hybrid energy system and the mathematical modeling of the main facilities of the ship are proposed. As shown in Figure 1, the ship consists of diesel generators (DG), solar panels (PV), battery energy storage system (BESS), hydrogen FC, and cold-ironing (CI) connection to meet the service and propulsion loads. The problem is formulated as a bi-level tri-objective stochastic programming problem to minimize the investment cost, operation cost, and emission, considering the uncertainties of the photovoltaic along the routine, which is depicted by finite discrete scenarios, as follows:

where x represents the routing, BESS sizing and hydrogen sizing optimization, i.e. $O_{t,ij}^{\mathrm{app}},O_{t,ij}^{\mathrm{cru}},O_{t-\Delta t,ij}^{\mathrm{dep}},O_{t,i}^{\mathrm{CI}},P_{rated}^{\mathrm{FC}},V_{\tan k}, P_{rated}^{BESS}, E_{rated}^{BESS}$. X represents the constraints for the optimal voyage routing, as shown in Eqs. 2–6; boundary limits of FC and BESS, i.e. $P_{rated}^{\mathrm{FC}},V_{\tan k},P_{rated}^{BESS},E_{rated}^{BESS}$ are within given intervals. $f_{inv}\left(x\right)$ is the investment cost of BESS and FC, i.e. $f_{fc,inv}+f_{bess,inv}$, as shown in Eqs. 12, 13, 19, and 20. y_s is the DG, BESS, CI output, etc., i.e. $V_{t,ij,s}^{\mathrm{dep}},V_{t,ij,s}^{\mathrm{cru}},V_{t,i,sj}^{\mathrm{app}},P_{t,s}^{\mathrm{PL}},P_{t,s}^{\mathrm{FC}},O_{t,s}^{\mathrm{FC}},V_{t,s}^{\mathrm{FC}},E_{t,s}^{BESS},P_{t,s}^{dis},P_{t,s,}^{ch},O_{t,s}^{dis},O_{t,s}^{ch},P_{t,n,s}^{DG},O_{t,n,s}^{DG},P_{t,i,s}^{\mathrm{CI}}$. ${\xi }_s$ is the solar irradiation along the routing under scenario s. $f_{op}\left(x,{\xi }_s\right):=f_{fc,op,s}+f_{bess,op,s}+f_{DG,op,s}+f_{\mathrm{CI},s}$ is the operation cost along the routing, i.e. the sum of operation cost of DG, FC, BESS, and CI. $f_{em}\left(x,{\xi }_s\right)=f_{DG,em,s}$ is the emission along the routing. $y_s\in Y\left(x,{\xi }_s\right)$ is the constraint set of the energy management problem, i.e. Eqs.7–10, 11, 16–18, 24–28, 30–32, 37–41. The models of voyage routing, FC, BESS, DG, PV, and CI are given as follows. w_s is the corresponding scenario probability.

FIGURE 1. Topology of the proposed AES.

Optimal Voyage Routing

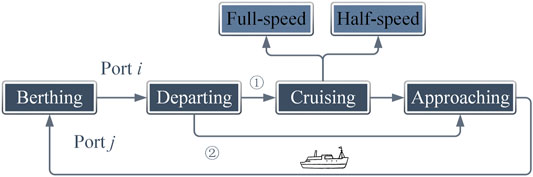
The sailing route of the ship increases the complexity of energy management optimization problem since it results in a variational total sailing time. As shown in Figure 2, generally, there are four travelling modes: departing mode, cruising mode, approaching mode, and berthing mode for the ship travelling from one port to another port. It is worth mentioning that the cruising mode is not always necessary considering the distance between two ports. Following are constraints that describe the ship travelling modes for the optimal voyage routing problem:

where k, i, and j are all sea ports along the sailing route of ship. Constraints (2)–(6) guarantee the navigation sequence by translating the diagram of travelling modes (Figure 2) into mathematical language, where all the variables that appear in the constraints are binary numbers. Eq. 2 denotes that after departing mode, a choice must be made between cruising mode and approaching mode since cruising mode is not always necessary for a short-distance cruise. Eq. 5 means that if the ship is going to berth at a port, it must approach the port in advance and depart to the next port afterwards. Eq. 6 shows that there is only one state existing during each time slot. Eq. 7 represents the voyage distance constraint, and Eqs. 8–10 limits the sailing speed in the required range to guarantee the security of shipboard power system.

FIGURE 2. Ship travelling modes between ports.

Since the voyage plan and power generation plan must be carried out simultaneously, the optimization problem is always considered as a joint power generation and voyage arrangement to ensure that the ship follows the sailing schedule and power requirements during operation. An exponential relationship between the propulsion load and the speed of ship is described as follows:

Fuel Cell Model

The size of the FC is optimized where the investment cost of the FC and hydrogen tank is considered. The sizing problem of the FC is solved in the upper level, which will be explained in Proposed solution approach, and the maximum power limit of the FC is considered as a constant utilized in the lower level. Since the space of shipboard area is limited, the size of the FC and hydrogen tank must be restricted at a reasonable level. The total investment cost of the FC can be expressed as:

Assuming that hydrogen fuel in the tank is fully charged at the beginning of the voyage in this study, the operation cost of the FC refers to the hydrogen consumption cost, which is expressed as:

To guarantee the reliability of the FC, as shown in Eq. 16, the total consumption of hydrogen must be less than the capacity of hydrogen tank, and the hydrogen retained in the tank must be higher than $\mu \%$ of the total capacity. The safety and effectiveness of the FC highly relies on the operating zone, where the output power of the FC is limited to reduce the consumption of hydrogen fuel. As shown in Figure 3, the FC should be operated in the range $\left[{\alpha }_{\mathrm{FC}},{\beta }_{\mathrm{FC}}\right]$ for the highest operation efficiency according to Eq. 17. Meanwhile, due to the slow dynamic response of the FC, Eq. 18 limits the ramp rate (ramp up/ramp down) in a certain range as well.

FIGURE 3. The relationship between the output power and operation efficiency of fuel cell.

Battery Energy Storage System Model

The BESS usually plays a crucial role in the operation of AESs, which brings economic benefits to operations, increases energy flexibility of regional markets, and improves the operating efficiency of system. In addition, the BESS can effectively alleviate the fluctuations caused by uncertainties such as renewable energy generation.

The size of the BESS is also optimized as another energy storage equipment in this study due to its high investment cost and limited space on ship, and by taking sizing problem into consideration, the energy management strategy could be more comprehensive. Therefore, the investment cost per sail can be calculated as:

After determining the size of the BESS in the upper level, $P_{\mathrm{rated}}^{\mathrm{BESS}}$ and $E_{\mathrm{rated}}^{\mathrm{BESS}}$ are considered as constants in the lower level where the discharging and charging process of the battery are conducted. In the meantime, the battery operation (degradation) cost is non-negligible, which mostly depends on the discharging power of BESS and can be considered as a constant value in most occasions. According to Tang et al. (2018), the operation cost parameter can be calculated through the Depth of Discharge (DoD) and rain-flow counting approach as shown in Eqs. 21, 22:

As shown in Eq. 23, a fourth-order relation is used to express the relationship between the depth of discharge and cycle life of the battery:

In this paper, the value of cost coefficient $C_{bess}$ is taken as a constant number from (Letafat et al., 2020). Following are the constraints that need to be followed during operation period of the BESS.

Eq. 24 denotes the energy balance of battery with charging and discharging process. Note that Eqs. 25, 26 show the energy capacity is limited by SOC (State-of-Charge). Eq. 27 limits the charging and discharging power of the battery, where $O_t^{\mathrm{dis}}$ and $O_t^{ch}$ are binary variables to denote the operation state of the battery, and Eq. 28 is used to prevent simultaneous charging and discharging processes to prolong the lifespan of BESS.

Diesel Generator Model

The operation cost and GHG of DGs are expressed as follows:

The power output limits and ramp up/down rates of DGs are expressed in Eqs. 31, 32:

Solar Power Model

The typical solar PV output model is adopted as follows (Wen et al., 2021):

Constraint Eq. 36 is introduced to limit the total variation distance of solar power output from the nominal distribution $w_s$.

Cold-ironing Model

Traditionally, seaports only provide regular logistics services to ships at berth, including berth allocation, loading and unloading of cargos, etc. However, when the ship is anchored in the port for cargo loading/unloading or ship maintenance, the generators of ships need to be kept running to meet the load requirements, which would cause serious GHG pollution. To avoid pollution in harbor area, cold-ironing technology becomes more popular to take the place of working-state diesel generators, and consequently, the unified dispatch model turns into off-grid and grid-connected modes. Eq. 36 shows the power transaction (purchasing) cost between ports and ship when the ship is berthing:

When the ship is connected to the shore power system, the capacity of electric energy transfer is limited to a certain range, and diesel generators should be turned off if the port energy covers the total load of the ship in order to save fuel resources and protect the atmospheric environment as follows:

Power Balance Of The Shipboard Power System

Along the routing periods, the power balance of shipboard power systems is depicted as follows:

Eq. 39 represents the power balance of the shipboard power system, which denote that the sum of the power output of DG, PV, FC, BESS, and cold-ironing needs to satisfy both propulsion loads $P_t^{\mathrm{PL}}$ and service loads $P_t^{SE}$ at an arbitrary time slot. Eq. 40 shows the calculation of service loads.

Proposed solution approach

Bi-level Tri-objective Optimization Method

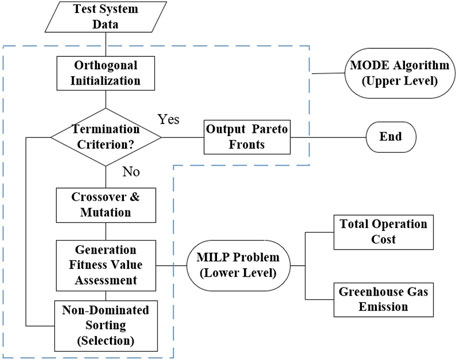
In this paper, since the voyage navigation and energy management problem are coordinated jointly as shown in Eq. (1), the optimization problem shows its complexity with a varying scheduling time. From the proposed mathematical model, a large number of variables including binary variables make the traditional optimization algorithm difficult to solve, and consequently, a bi-level multi-objective optimization method is put forward in this section, considering the two-stage nature of voyage routing and energy management of AESs.

In the upper level, a differential evolution algorithm for multi-objective optimization is utilized to optimize x and ρ weight between the cost and emission. Differential evolution algorithm adopts real number coding and executes three main operators in sequence, which are mutation, hybridization, and selection (Ao and Hong, 2011). In this paper, the differential evolution uses the DE/rand/1 strategy to mutate.

Then, the hybridization operation is used between the mutated vector and the target vector to increase the diversity of population. Also, the elite retention strategy guarantees the increase of speed of convergence to the optimal solution. The basic process of MODE in this paper is described as follows: Firstly, orthogonally initialize the population with the required population size, and set the differential control parameters. Then, the population group performs differential evolution operations such as mutation and crossover operations to produce the offspring population. After combining offspring with the initial population, the intensity Pareto value of the individuals are calculated and sorted, where the individuals with higher rank and less crowded density will become the next generation group. If the termination criterion of algorithm is met, the corresponding Pareto optimal solution set will be the final output, or else, the differential evolution operations will be performed again for the next generation.

The lower level is solved for the energy management of AESs, which is solved by commercial tools. In this level, the specific energy management plan is calculated, where the results of two objective functions are invocated as fitness values in the upper level. It should be noticed that the constraint (Eq. 10) shows its non-convexity due to the cubic relationship between propulsion power and ship speed, and the nonlinear constraint brings great pressure on solving the optimization problem. In this paper, the piecewise linearization method is applied with better analysis results. Then, the problem can be described as a mixed-integer linear programming (MILP) problem and can be easily solved by GUROBI.

The whole process is described in Figure 4, which represents the combination of both upper level and lower level.

FIGURE 4. Flow chart of the proposed bi-level algorithm.

Description Of bi-level Mathematical Model

In the upper level, the multi-objective differential evolution algorithm is utilized, and the mathematical model can be described as:

s.t. (1)–(5) $P_{\mathrm{rated}}^{\mathrm{FC}}\in \left[0,P_{\max }^{\mathrm{FC}}\right],V_{\tan k}\in \left[0,V_{\tan k,\max }\right],P_{\mathrm{rated}}^{\mathrm{BESS}}\in \left[0,P_{\max }^{\mathrm{BESS}}\right],E_{\mathrm{rated}}^{\mathrm{BESS}}\in \left[0,E_{\max }^{\mathrm{BESS}}\right]$.where $\rho \in \left[\mathrm{0,1}\right]$ represents the weight factor between the two contradictory objective functions. The second-line and third line of problem (Eq. 42) can be converted into linear programming problems using Lagrange duality.

In the lower level, the weight factor ${\rho }^{\ast }$ converts the multi-objective function to a single objective function. Given the navigation routing plan from the upper level, the model can be optimized as an MILP problem for shipboard power scheduling.

s.t., Eqs. (7)–(10), (11), (16)–(18), (24)–(28), (30)–(32), (38)–(41).

This MILP problem is solved through GUROBI, which is a commercial tool with high computation efficiency. It should be noted that, for a given x, the problem (Eq. 43) can be solved in parallel for each scenario.

The whole procedure of two stages circulates until the stopping criteria are met with a final Pareto front result and its corresponding energy management strategy.

Simulation results

Case Description

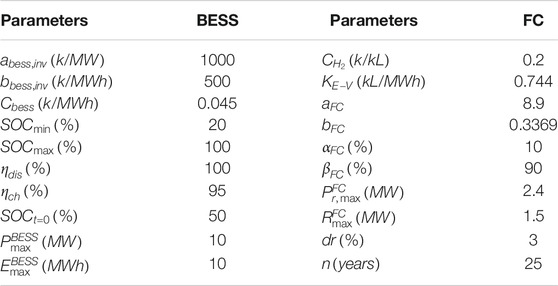
In this study, a cargo ship with two DGs, an FC, a BESS, and a solar panel sailing from Dalian, China, to Singapore is used to verify the proposed method. As shown in Figure 5, there are four potential intermediate ports, including Qingdao, Shanghai, Zhoushan, and Hong Kong, where the total distance of voyage is 5200 km. For instance, the ship can depart from Dalian and sail to Singapore directly, or the ship can pass through Qingdao and Shanghai as intermediate ports to Singapore, or else the ship can stop at all the ports along the route. There are four scenarios to represent the uncertainties of PV along the routine. The specific voyage plan will be optimized by the proposed optimization method as introduced in Proposed solution approach. The parameters of diesel generators and power limits are given in Table 1. The parameters of diesel BESS and FC are given in Table 2. The parameters of navigation are given in Table 3.

TABLE 1. Parameters of diesel generators and power limits

TABLE 2. Parameters of diesel BESS and FC

TABLE 3. Parameters of navigation

FIGURE 5. Navigation routes with intermediate ports and distances.

Optimized Result Analysis

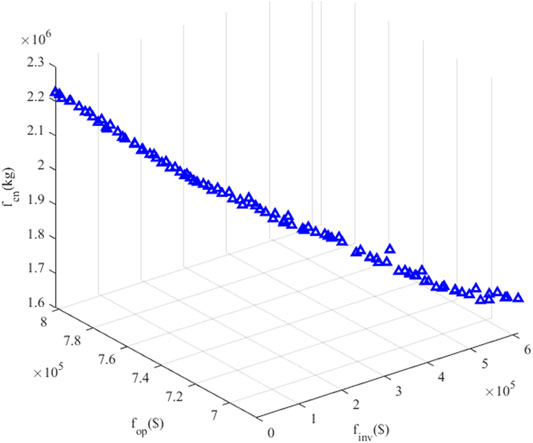
The optimized result is analyzed in this sub-section. The simulation of the proposed problem is performed on a PC with a 2.6 GHz Intel(R) Core (TM) i7-9750H CPU and 8.00 GB of RAM. Based on the MODE settings shown in Table 4, the Pareto Front of the proposed optimization problem is illustrated in Figure 6. There are two objective functions according to Eq. 40 in this paper, and when the improvement of one objective function will inevitably weaken the other function, the corresponding solution is called the Pareto Solution or non-dominated solution. The curved surface formed by the Pareto optimal set, which is the set of optimal solutions for the objective functions, is called the Pareto front surface. From Figure 6, it can be concluded that the multi-objective optimization problem has well converged with a perfect Pareto front curve, and the specific result of costs are calculated through the weight between two objective functions, which is optimized in the upper level.

TABLE 4. Parameters of MODE setting

FIGURE 6. Pareto front of the proposed optimization problem.

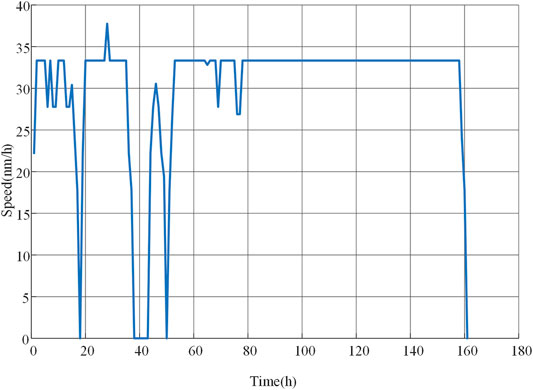
The optimized navigation routine is presented in Figure 7, where the cargo ship departs from Dalian; berths at Qingdao, Shanghai, and Zhoushan; and arrives in Singapore (time 161 h). During most time periods, the ship sails at the cruising mode with a slight variation of speed. In this scenario, investment cost is 620.16 k$, operation cost is 747.87 k$, greenhouse gas emission is 2005.8 tons, proposed FC installment capacity is 2 MW, and proposed BESS installment capacity is 10 MWh/9 MW.

FIGURE 7. Optimized navigation routine and ship speed.

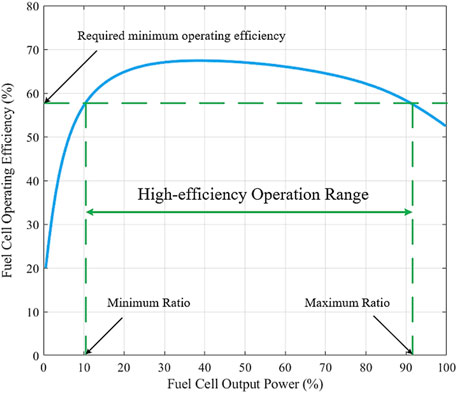
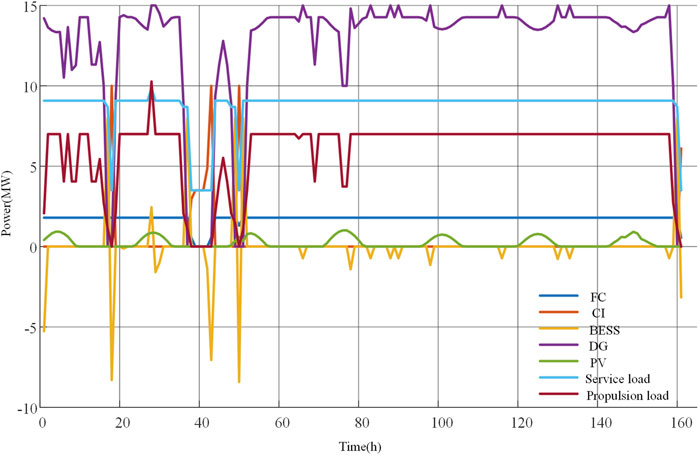
Generation scheduling of the shipboard power system is shown in Figure 8. From the diagram, the ship berths at three ports during the periods 18 h, 38–43 h, and 50 h, and the port power systems (red curve) are mainly responsible for the power needs of the ship, including service loads (green curve) and the charging state of BESS (yellow curve). The propulsion power is related to the cruising mode of ship, which follows the pattern of cruising speed in Figure 7, and when the ship berths at ports, the propulsion power reduces to zero naturally. From Shanghai to Zhoushan, the ship sails only under departing and approaching mode due to the rather short voyage distance, and consequently, the propulsion load is low compared to the voyage under cruising mode. The FC has a steady power output during most of the shipping time, and because its operation cost is cheaper than DGs, the FC always operates at the maximum ratio within the high-efficiency operation range and ramp range. Although the solar panel generates a limited amount of power because of the restricted area on the ship, it also can alleviate the power shortage in the islanded mode and cooperate with BESS to better serve the power needs of the electrical ship. The cyan curve stands for the power output of DGs, and as the major source of GHG emissions, DGs are operated under a less steady state, especially in the periods that the BESS discharges or the port supplies power in berthing mode. Note that there are two DGs working in the meantime due to their identical characteristics, and consequently, the ramp up or down rates of DGs are satisfied during the discharging periods of batteries.

FIGURE 8. Generation scheduling of shipboard power system.

Comparison Scenarios Analysis

To verify the effectiveness of the proposed optimization algorithm, six different scenarios are conducted considering the navigation routine and power equipment.

Case 1: Optimized result of the proposed algorithm

Case 2: The navigation routine without any stop between Dalian and Singapore

Case 3: The all-electric ship without BESS installed

Case 4: The all-electric ship without FC installed

Case 5: The all-electric ship without CI technology

Case 6: The price of CI is set to 0.001 of the previous price.

The results are presented in Table 5, where operation costs, GHG emissions, the total sailing time, the hybrid-ESS energy, and the power capacity are included, and analysis is also given below. Three typical Pareto front results (Cases 1, 4, and 6) are compared in Figure 9. The total cost is separated as the investment cost and operation cost. It can be found that due to the installment of the BESS, FC, and renewable PV module, the investment cost of the proposed algorithm is highest. But the operation cost and greenhouse gas emission are the lowest among all the cases. From another aspect, with the increase of capacity of installed BESS, FC, and PV, the greenhouse gas emission will be reduced further. The zero emission is also possible in some application levels. However, it will be restricted by a lot of factors like the size, weight, and investment cost. The proposed algorithm also reduces the sailing time significantly.

TABLE 5. Result comparison of six cases

FIGURE 9. Comparison of Pareto fronts in Cases 1, 4, and 6.

Case 2: In this scenario, the navigation routine is not optimized in the model and instead, the ship sails from Dalian to Singapore directly without any stop. The long shipping distance brings great pressure to the shipboard power system, which results in maximum BESS energy capacity (10 MWh), power capacity (10 MW), and fuel cell capacity (2 MW). The operation cost in this case increases dramatically (807.35 k$) as the ESSs cannot be charged by the utility grid. Also, without the optimization of the sailing routine, the greenhouse gas emission rises slightly, although the total sailing time drops by 1 h.

Case 3: In this scenario, the navigation routine is optimized while the BESS is uninstalled in the proposed shipboard power system. The total cost decreases to 3230.36 k$ because of zero investment cost on battery. However, the operation cost of other facilities has an increasing tendency since the BESS plays a significant role in the efficiency and BESS would cause fluctuations from the uncertainties in power system. For instance, the greenhouse gas emission goes up by 10.91% without the exploitation of the BESS, which is unacceptable according to the requirement of IMO. It is also proved that the BESS brings flexible operation for the ship microgrid and also compensates for the power imbalance from loads and solar power.

Case 4: In this scenario, the fuel cell is not exploited, which leads to a significant rise on both operation cost (796.71 k$) and greenhouse gas emissions (2208.4 ton). FC gains much attention due to its environment-friendly nature and low operation cost, and the lack of FC in this scenario means that DGs must generate more power, and larger capacity of BESS (48 MWh) is needed to balance the propulsion and service loads, and inevitably, more pollution is produced simultaneously that contributes to the highest value of all six cases. From Figure 9, the Pareto front result also shows an obvious increase of operation cost and GHG emission compared with the proposed case 1, representing that the FC plays a significant part in AESs and hybrid-ESS is necessary when designing the AESs.

Case 5: In this scenario, the cold-ironing technology is not allowed to use, which means that the ship cannot make transactions with the port microgrids. The total sailing time decreases to 174 h without CI technology. The reason is that when the ship berths at ports, DGs must work steadily to satisfy the service loads, and batteries cannot be charged during those periods, and consequently, the ship tends to reduce the berthing time without the variation of sailing route. It also perfectly explains the slight increment on operation cost and GHG emission in this scenario. The CI technology can effectively reduce the air pollution in harbor areas and becomes more and more popular in recent years.

Case 6: In this scenario, the impacts of CI prices on the navigation routing and energy management of AESs are explored. A direct observation is that, the sailing time is increased to 183 h, indicating the AESs can always berth within ports, as the prices are almost 0. It decreases the requirements on the capacity of BESSs, as the power capacity is decreased to 8 MW. It further decreases the investment cost by 25.95%.

Sensitivity Analysis

To further demonstrate the superiority of the proposed method, a sensitivity analysis is conducted by testing the effect of weight parameter between operation cost and GHG emission. In this scenario, a series of weights for operation cost are given in advance instead of being optimized in the upper level of the proposed method. From the result shown in Figure 10, it can be observed that the emission is increasing with the increase of weight, as the emission and cost have not been converted into the same unit and the emission is much higher than the operation cost.

FIGURE 10. Sensitivity analysis of weight for operation cost.

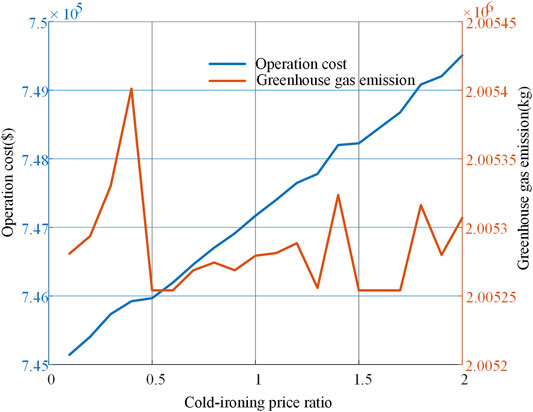
To further verify the impacts of CI prices on the operation cost and emission, a sensitive analysis is performed on the CI prices of case 1. The results are shown in Figure 11. It can be observed that the increase of CI prices always leads to a high operation cost, while not linearly, especially when the prices are increased by one to two times; the BESS and FC can be used to reduce the operation cost. The increase of CI prices does not affect the emission heavily, as the CI cost only occupies 3% of total operation cost, which is much smaller than the emission.

FIGURE 11. Sensitivity analysis of cold-ironing price ratio.

Conclusion

In this paper, a coordinated navigation routing and power generation scheduling problem is studied, which aims at making a compromise between total operation cost and greenhouse gas emissions under practical operation constraints of a ship. A novel maritime hybrid energy configuration that combines DG, BESS, FC, PV, and CI connection is presented with a real-world navigation routine from Dalian to Singapore. The problem is solved through a bi-level multi-objective differential evolution algorithm, where navigation parameters, capacity of the BESS and FC, and weight between contradictory objective functions are optimized in the upper level and specific power generation scheduling is settled in the lower level. Six case studies are conducted to verify the effectiveness of proposed algorithm, and the simulation results show that the coordinated navigation routing and power generation scheduling model can reduce the total operation cost of the ship while minimizing the greenhouse gas emissions, and each member of system configuration plays a significant role in the optimal management strategy since the lack of any facility would lead to the increase of operation cost and pollution emission. In future works, more complicated navigation routing problems will be studied such as different destinations and restrictions, and hydrogen charging stations will be implemented to further make use of fuel cells for less greenhouse gas emissions.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, writing—original draft XP; data curation, software, XZ; investigation, FZ.

Funding

This work was supported by Basic Research Plan in Shenzhen City (Grant No. JCYJ20180507181539943, JCYJ20190806142618203, JCYJ20210324120404013, and GXWD20201230155427003-20200801194851008).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Glossary

Acronyms

AES All electric ship

BESS Battery energy storage system

CRF Capital recovery factor

CI Cold-ironing technology

DG Diesel generator

EEOI Energy efficiency operational indicator

FC Fuel cell

GHG Greenhouse gas emission

MODEA Multi-objective differential evolution algorithm

MILP Mixed-integer linear programming

NSGA-II Non-dominated sorting genetic algorithm II.

PV Photovoltaic

SOC State of charge

Indices

i, j, k Index of ports along the route

n Index of diesel generators

t Index of voyage time periods

Parameters

${\mathit{\alpha }}_{\mathit{FC}}$,${\mathit{\beta }}_{\mathit{FC}}$ High-efficiency operation range of fuel cell

${\mathit{\eta }}_{\mathit{c}\mathit{h}}$,${\mathit{\eta }}_{\mathit{dis}}$ Charging and discharging efficiency of BESS.

${\mathit{\eta }}_{\mathit{PV}}$ Instantaneous efficiency of PV modules

${\mathit{\eta }}_{\mathit{tan}\mathit{k}}$ Fuel transmission efficiency of hydrogen tank

$\mathit{\mu }$ Percentage of hydrogen remained in the hydrogen tank

${\mathit{a}}_{\mathit{DG},\mathit{g}\mathit{e}}$,${\mathit{b}}_{\mathit{DG},\mathit{g}\mathit{e}}$ Greenhouse gas emission coefficients of DGs (ton/MWh)

${\mathit{a}}_{\mathit{DG},\mathit{o}\mathit{p}}$,${\mathit{b}}_{\mathit{DG},\mathit{o}\mathit{p}}$ Fuel consumption coefficients of DGs (k$/MWh)

${\mathit{a}}_{\mathit{BESS}}$,${\mathit{b}}_{\mathit{BESS}}$ Investment coefficients of BESS

${\mathit{a}}_{\mathit{FC}}$,${\mathit{b}}_{\mathit{FC}}$ Hydrogen consumption coefficients

${\mathit{a}}_{\mathit{FC}, \mathit{i}\mathit{n}\mathit{v}}$ Investment coefficient of FC

${\mathit{A}}_{\mathit{PV}}$ Panel installation area (m²)

${\mathit{C}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{s}}$ Degradation cost coefficient of BESS (k$/MWh)

$\mathit{C}\mathit{R}\mathit{F}$ Capital recovery factor

${\mathit{C}}_{{\mathit{H}}_2}$ Price of liquid hydrogen (k$/kL)

${\mathit{c}}_{\mathit{p}1}$,${\mathit{c}}_{\mathit{p}2}$ Voyage proportional and exponential coefficients

${\mathit{C}}_{\mathit{tan}\mathit{k},\mathit{i}\mathit{n}\mathit{v}}$ Rent (investment) cost of hydrogen tank (k$)

${\mathit{D}}_{\mathit{i}\mathit{j}}$ Distance between port i and port j (km)

F Scale factor of perturbation

${\mathit{K}}_{\mathit{E}-\mathit{V}}$ Volume of liquid hydrogen required by fuel cell to produce specific amount of energy (kL/MWh)

${\mathit{N}}_{\mathit{s}\mathit{a}\mathit{i}\mathit{l}}$ Sailing times per year during the service life of BESS

${\mathit{P}}_{\mathit{i},\mathit{min}}^{\mathit{CI}}$,${\mathit{P}}_{\mathit{i},\mathit{max}}^{\mathit{CI}}$ Minimum and maximum power transfer capacity between ship and the i^th port

${\mathit{P}}_{\mathit{n},\mathit{min}}^{\mathit{DG}}$,${\mathit{P}}_{\mathit{n},\mathit{max}}^{\mathit{DG}}$ Minimum and maximum power output of the nth diesel generator (MW)

${\mathit{P}}_{\mathit{L},\mathit{d}\mathit{e}\mathit{p}}$,${\mathit{P}}_{\mathit{L},\mathit{c}\mathit{r}\mathit{u}}$,${\mathit{P}}_{\mathit{L},\mathit{a}\mathit{p}\mathit{p}}$,${\mathit{P}}_{\mathit{L},\mathit{b}\mathit{e}\mathit{r}}$ Different service loads under four cruising modes

${\mathit{R}}_{\mathit{n},\mathit{max}}^{\mathit{DG}}$ Maximum ramp up/down speed of the nth diesel generator (MW/h)

${\mathit{R}}_{\mathit{max}}^{\mathit{FC}}$ Maximum ramp up/down speed of fuel cell (MW/h)

$\mathit{S}\mathit{O}{\mathit{C}}_{\mathit{min}}$,$\mathit{S}\mathit{O}{\mathit{C}}_{\mathit{max}}$ Minimal and maximal state-of-charge of BESS

${\mathit{V}}_{\mathit{min}}^{\mathit{a}\mathit{p}\mathit{p}}$, ${\mathit{V}}_{\mathit{max}}^{\mathit{a}\mathit{p}\mathit{p}}$ Minimal and maximal ship speed at approaching mode (km/h)

${\mathit{V}}_{\mathit{min}}^{\mathit{c}\mathit{r}\mathit{u}}$, ${\mathit{V}}_{\mathit{max}}^{\mathit{c}\mathit{r}\mathit{u}}$ Minimal and maximal ship speed at cruising mode (km/h)

${\mathit{V}}_{\mathit{min}}^{\mathit{d}\mathit{e}\mathit{p}}$, ${\mathit{V}}_{\mathit{max}}^{\mathit{d}\mathit{e}\mathit{p}}$ Minimal and maximal ship speed at departing mode (km/h)

${\mathit{V}}_{\mathit{tan}\mathit{k}}$ Capacity of hydrogen tank for fuel cell

Variables

${\mathit{C}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{s},\mathit{i}\mathit{n}\mathit{v}}$ Investment cost of BESS

${\mathit{C}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{s},\mathit{o}\mathit{p}}$ Operation cost of BESS

${\mathit{C}}_{\mathit{CI}}$ Total cold ironing cost

${\mathit{C}}_{\mathit{CI},\mathit{t},\mathit{i}}$ Electricity price at port i during time slot t

${\mathit{C}}_{\mathit{DG},\mathit{g}\mathit{e}}$ Greenhouse gas emission of DGs

${\mathit{C}}_{\mathit{DG},\mathit{o}\mathit{p}}$ Total operation cost of DGs

${\mathit{C}}_{\mathit{f}\mathit{c},\mathit{i}\mathit{n}\mathit{v}}$ Investment cost of FC.

${\mathit{C}}_{\mathit{f}\mathit{c},\mathit{o}\mathit{p}}$ Operation cost of fuel cell

${\mathit{E}}_{\mathit{rated}}^{\mathit{BESS}}$ Rated capacity of BESS (to be optimized in the upper level)

${\mathit{E}}_{\mathit{t}}^{\mathit{BESS}}$ Residual energy stored in BESS

${\mathit{I}}_{\mathit{t}}^{\mathit{PV}}$ Solar irradiation during time slot t

${\mathit{P}}_{\mathit{rated}}^{\mathit{BESS}}$ Rated power of BESS (to be optimized in the upper level)

${\mathit{P}}_{\mathit{rated}}^{\mathit{FC}}$ Rated power of FC (to be optimized in the upper level)

${\mathit{P}}_{\mathit{t}}^{\mathit{c}\mathit{h}},{\mathit{P}}_{\mathit{t}}^{\mathit{dis}}$ Charging and discharging power of BESS

${\mathit{P}}_{\mathit{t},\mathit{i}}^{\mathit{CI}}$ Cold-ironing power at port I during time slot t

${\mathit{P}}_{\mathit{t},\mathit{n}}^{\mathit{DG}}$ Power output of the nth DG during time slot t

${\mathit{P}}_{\mathit{t}}^{\mathit{FC}}$ Power output of fuel cell during time slot t

${\mathit{P}}_{\mathit{t}}^{\mathit{P}\mathit{L}}$ Propulsion load of ship during time slot t

${\mathit{P}}_{\mathit{t}}^{\mathit{PV}}$ Power output of solar panels during time slot t

${\mathit{P}}_{\mathit{t}}^{\mathit{S}\mathit{E}}$ Service load of ship during time slot t

${\mathit{O}}_{\mathit{t},\mathit{i}\mathit{j}}^{\mathit{a}\mathit{p}\mathit{p}}$ Binary variable denoting the approaching mode from port i to j

${\mathit{O}}_{\mathit{t}}^{\mathit{c}\mathit{h}}$, ${\mathit{O}}_{\mathit{t}}^{\mathit{dis}}$ Binary variable denoting the operation state of BESS during time slot t

${\mathit{O}}_{\mathit{t}}^{\mathit{dis}}$ Binary variable denoting the cruising mode from port i to j

${\mathit{O}}_{\mathit{t},\mathit{i}}^{\mathit{CI}}$ Binary variable denoting the berthing (cold-ironing) mode at port i

${\mathit{O}}_{\mathit{t},\mathit{i}\mathit{j}}^{\mathit{d}\mathit{e}\mathit{p}}$ Binary variable denoting the departing mode from port i to j

${\mathit{O}}_{\mathit{t},\mathit{n}}^{\mathit{DG}}$ Binary variable denoting on/off state of the nth DG during time slot t

${\mathit{O}}_{\mathit{t}}^{\mathit{FC}}$ Binary variable denoting on/off state of fuel cell during time slot t

${\mathit{V}}_{\mathit{t},\mathit{i}\mathit{j}}^{\mathit{a}\mathit{p}\mathit{p}}$ Approaching speed of ship from port i to j during time slot t

${\mathit{V}}_{\mathit{t},\mathit{i}\mathit{j}}^{\mathit{c}\mathit{r}\mathit{u}}$ Cruising speed of ship from port i to j during time slot t

${\mathit{V}}_{\mathit{t},\mathit{i}\mathit{j}}^{\mathit{d}\mathit{e}\mathit{p}}$ Departing speed of ship from port i to j during time slot t

${\mathit{v}}_{\mathit{i}}\left(\mathit{t}\right)$ Mutated vector of differential evolution algorithm

${\mathit{x}}_{\mathit{b}\mathit{e}\mathit{s}\mathit{t},\mathit{i}}\left(\mathit{t}\right)$ The best individual vector in the t^th generation population

${\mathit{x}}_{{\mathit{r}}_{\mathit{i}}}\left(\mathit{t}\right)$ Different dimensions of the t^th individual vector