Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kovalenko, Igor N.
1994.
Rare events in queueing systems?A survey.
Queueing Systems,
Vol. 16-16,
Issue. 1-2,
p.
1.
Embrechts, P.
and
Klüppelberg, C.
1994.
Some Aspects of Insurance Mathematics.
Theory of Probability & Its Applications,
Vol. 38,
Issue. 2,
p.
262.
Novak, S. Yu.
1997.
On the Distribution of the Ratioof Sums of Random Variables.
Theory of Probability & Its Applications,
Vol. 41,
Issue. 3,
p.
479.
Diaz, Francisco J.
1999.
Identifying Tail Behavior by Means of Residual Quantile Functions.
Journal of Computational and Graphical Statistics,
Vol. 8,
Issue. 3,
p.
493.
Zeevi, Assaf
and
Glynn, Peter W.
2004.
Estimating tail decay for stationary sequences via extreme values.
Advances in Applied Probability,
Vol. 36,
Issue. 1,
p.
198.
Duffy, Ken R.
and
Meyn, Sean P.
2011.
Estimating Loynes’ exponent.
Queueing Systems,
Vol. 68,
Issue. 3-4,
p.
285.




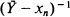 where
where 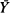 is the mean of the sample values overshooting
is the mean of the sample values overshooting 