1. 引言
考虑有限和优化问题:
, (1)
其中分量函数
连续可微,假设
是强凸的。机器学习中满足条件的优化问题有很多,例如带
正则项的逻辑回归问题和带
正则项的最小平方回归问题等 [1] [2] [3] 。
当数据规模过大时,随机梯度下降(SGD)算法 [4] 是求解问题(1)的主流算法,即用随机梯度估计全梯度,其迭代格式为
,
其中
是步长,
是分量函数
在
处的梯度。随机梯度
与全梯度
之间的方差导致SGD即使在强凸条件下,也只能达到次线性收敛速度 [5] 。方差缩减梯度(SVRG)算法 [6] 通过内外两层循环达到缩减方差的目的,但由于其在外循环中需要计算全梯度且内循环次数较大,导致数据规模过大时计算量大。为了改善这个问题,SCSG [7] 令内循环次数服从几何分布且在外循环中计算批量梯度
,
其中
,
为
的批量大小,
为在外循环中设置的快照点。在内循环中,SCSG用与SVRG相同的格式更新梯度估计量:
。
在强凸条件下,其使用固定批量可线性收敛到解的邻域。SCSG适用于求解大规模
、低精度
的优化问题 [7] [8] [9] ,可以经过很少的有效循环次数收敛到上述目标精度。
步长是保证随机梯度类算法收敛的关键因素,很小的常数步长和衰减步长都会使算法收敛缓慢,并且手动调整常数步长的过程相当耗时 [10] [11] [12] 。Polyak步长 [13] 利用迭代过程中产生的函数值和梯度自动地计算步长,避免了手动调整的过程,其计算公式为
,
其中
是
的极小值。为了将Polyak步长与随机梯度类算法结合,Loizou等人 [14] 提出Polyak步长的随机版本(SPS):
,
其中
是
的极小值。SGD结合SPS步长比结合固定步长数值表现好。当SPS步长中
不易求解时,可用一个下界
来替换 [15] 。最近,Wang等人 [16] 介绍了1/t-带步长,其允许步长在一定范围内扰动,具体格式为
,
,
其中
是正常数。显然,衰减步长
是1/t-带步长的特殊情况。
受1/t-带步长和Polyak步长启发提出1/t-Polyak步长,并将其与SCSG结合提出新的算法——SCSGP。在强凸光滑的条件下,SCSGP结合变化的批量可达到线性收敛速度。数值实验结果表明SCSGP比SCSG及其他随机梯度类算法表现好。
论文其余部分概括如下:在第2部分中提出1/t-Polyak步长并描述SCSGP算法。收敛性分析在第3部分。在第4部分中设置了数值实验。最后在第5部分进行总结。
2. 1/t-Polyak步长与SCSGP算法
首先,利用Polyak步长的随机版本并将其与1/t-带步长结合,提出1/t-Polyak步长:
(2)
其中
形式如下:
,
其中
为批量函数
的极小值,
用于调整步长的范围,由用户给定。对于一些非负的损失函数,根据批量函数的定义可取
。结合1/t-Polyak步长和SCSG算法提出SCSGP算法,见算法1。
在SCSGP算法的第t次外循环中,内循环次数
是非负的几何随机变量,其概率分布为
,
。值得注意的是,SCSG中
取固定值,但在SCSGP中
随迭代次数变化。若
,则有
,
其中
记为对
取期望。该性质在后续分析中起到重要作用。另外不难发现
是梯度估计量
的有偏估计:
, (3)
其中
。
3. 收敛性分析
由于几何随机变量
在收敛分析中占据重要地位,需要给出下面关键的引理。
引理1 [8] 由于
,其中
,则对任意满足
的序列
有
,
其中E记为对所有随机变量取期望。
记
,则对任意
有
。 (4)
为了应用(3),需要证明用到的相关序列
满足
。下面引理保证了该性质。
引理2 假设
是L-光滑的,令
且
,则对任意
,
,
,
,
,
。
证明:因为
是L-光滑的和(3),可得
(5)
其中最后一个不等式利用了 [8] 中引理B.2。由于对任意
有
,令
,则有
。 (6)
因为
,
且
,可知
。由(5)和(6)得到
(7)
注意到
,用类似(5)的推导过程可得
(8)
再次使用
并取
,则有
,
。
将上述不等式和(7)代入(8)得到
(9)
由
和
可得
结合上式和(9)有
(10)
为了证明
和
的上界,记
对(10)取全期望得到
由
可得
于是有
即
分别用
替换
,用
替换
,由 [8] 中引理B.3得到
,这表明
和
。由(7)可知
。利用
可得
和
。结论得证。
现在分析强凸条件下SCSGP的线性收敛速度。
定理1 假设
是L-光滑的且
是
-强凸的,令
,
,则
其中
,
,
和
证明:由 [8] 中引理B.3和等式(20)得到
(11)
由
,
和
可得
其中第三个不等式用了
。另外,
。
将上述两个系数代入(11),并再次使用
得到
(12)
因为f是
-强凸的,可得
其中第二个不等式利用了
。重新整理上式得
将上式代入(12)得到
替换
和
,然后两边同除
可得
其中最后一个不等式成立是因为
。上式可以写为
(13)
将
时的(13)累加求和得到
(14)
重新整理(14),证毕。
4. 数值实验
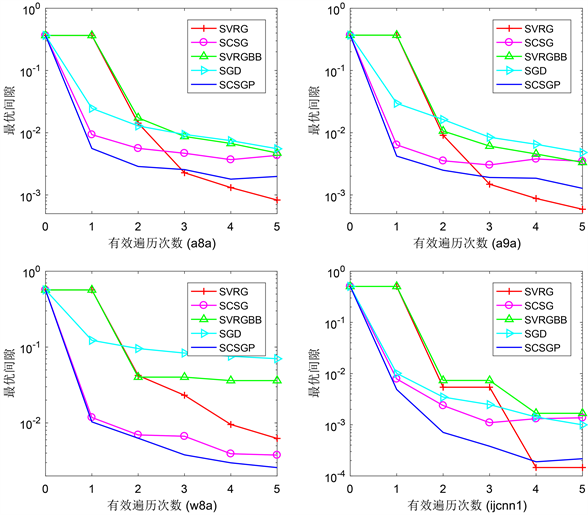
Figure 1. Comparison of different stochastic gradient algorithms
图1. 不同随机梯度类算法的对比
考虑正则化的逻辑回归问题
其中
是给定的训练集。 [7] 中指出内循环次数
取期望值有助于增加SCSG算法的稳定性,且从
中选取
可以减小计算代价,所以在实验中设置
(几何随机变量
的期望)且从
中选取
,其中
记为向下取整。为了验证SCSGP的有效性,比较SCSGP、SCSG、SVRG、SVRGBB和SGD。具体地,SVRG中设置小批量
;SCSG设置
,
,
;SCSGP设置
,
,
。表1给出LIBSVM (网址: https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/)中四个标准数据集的信息。用表2的参数值进行对比实验,最优间隙随有效循环次数变化情况见图1。SCSGP明显比SCSG表现好,并且在前几个有效循环次数中,SCSGP与其它随机梯度类算法相比具有更好的数值结果。

Table 1. The information of data sets
表1. 数据集信息

Table 2. Parameters used for experiments
表2. 实验中的参数设置
5. 总结
基于Polyak步长和1/t-带步长提出1/t-Polyak步长,并将该步长与SCSG结合提出SCSGP算法。当目标函数强凸光滑时,SCSGP线性收敛。数值实验考虑正则化的逻辑回归问题,实验结果表明在前几个有效循环次数中SCSGP比其他随机梯度类算法表现好。