| Citation: |
Guenbo Hwang. ANALYTICAL SOLUTION FOR THE TWO-DIMENSIONAL LINEAR ADVECTION-DISPERSION EQUATION IN POROUS MEDIA VIA THE FOKAS METHOD[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2334-2354. doi: 10.11948/20200383
|
ANALYTICAL SOLUTION FOR THE TWO-DIMENSIONAL LINEAR ADVECTION-DISPERSION EQUATION IN POROUS MEDIA VIA THE FOKAS METHOD
-
Abstract
We present the analytical solution of the two-dimensional linear advection-dispersion equation ($ 2 $-D LAD) in the quarter plane and the semi-infinite domain for two-dimensional solute transport in a porous medium. The governing equation includes terms describing advection, longitudinal and transverse dispersions and linear equilibrium adsorption. The analytical solution in terms of integrals in the complex plane is established by utilizing the unified transform method, also known as the Fokas method. The method hinges upon analysis of the divergence form of the governing equation and the so-called global relation, which is an algebraic relation coupling all known and unknown initial and boundary values. Particularly, the integral representation of the solution yields an accurate and fast numerical evaluation of the solution for the $ 2 $-D LAD equation. We demonstrate examples as an application of the developed solution and compare the analytical solution with numerical results.
-
-
References
[1] V. Batu, A generalized two-dimensional analytical solution for hydrodynamic dispersion in bounded media With the first-type boundary condition at the source, Water Resour. Res., 1989, 25, 1125-1132. doi: 10.1029/WR025i006p01125 [2] G. Biondini and G. Hwang, Initial-boundary value problems for discrete evolution equations: discrete linear Schrödinger and integrable discrete nonlinear Schrödinger equations, Inv. Probl., 2008, 24, 065011(1-44). [3] J. Chen and C. Liu, Generalized analytical solution for advection-dispersion equation in finite spatial domain with arbitrary time-dependent inlet boundary condition, Hydro. Earth Syst. Sci., 2011, 15, 2471-2479. doi: 10.5194/hess-15-2471-2011 [4] J. Chen, J. Chen, C. Liu, C. Liang and C. Lin, Analytical solutions to two-dimensional advection-dispersion equation in cylindrical coordinates in finite domain subject to first- and third-type inlet boundary conditions, J. Hydrology., 2011, 405, 522-531. doi: 10.1016/j.jhydrol.2011.06.002 [5] M. J. Colbrook, Extending the unified transform: curvilinear polygons and variable coefficients PDEs, IMA J. Numer. Anal., 2020, 40, 976-1004. doi: 10.1093/imanum/dry085 [6] M. J. Colbrook, L. J. Ayton and A. S. Fokas, The unified transform for mixed boundary condition problems in unbounded domains, Proc. Roy, Soc. A., 2019, 475, 20180605. doi: 10.1098/rspa.2018.0605 [7] M. J. Colbrook, Z. I. Botev, K. Kuritz and S. MacNamara, Kernel density estimation with linked boundary conditions, Stud. Appl. Math., 2020, 145, 357-396. doi: 10.1111/sapm.12322 [8] M. J. Colbrook, N. Flyer and B. Fornberg, On the Fokas method for the solution of elliptic problems in both convex and non-convex polygonal domains, J. Comput. Phys., 2018, 374, 996-1016. doi: 10.1016/j.jcp.2018.08.005 [9] M. J. Colbrook, A. S. Fokas and P. Hashemzadeh, A hybrid analytical-numerical technique for elliptic PDEs, SIAM J. Sci. Comput., 2019, 41, A1066-A1090. doi: 10.1137/18M1217309 [10] F. R. J. de Barros, M. J. Colbrook and A. S. Fokas, A hybrid analytical-numerical method for solving advection-dispersion problems on a half -line, Int. J. Heat Mass Transf., 2019, 139, 482-491. doi: 10.1016/j.ijheatmasstransfer.2019.05.018 [11] G. Dagan, Theory of solute transport by groundwater, Ann. Rev. Fluid Mech., 1987, 19, 183-215. doi: 10.1146/annurev.fl.19.010187.001151 [12] B. Deconinck, B. Pelloni and N. E. Sheils, Non-steady-state heat conduction in composite walls, Proc. Roy, Soc. A., 2014, 470, 20130605. doi: 10.1098/rspa.2013.0605 [13] B. Deconinck, T. Trogdon and V. Vasan, The method of Fokas for solving linear partial differential equations, SIAM Review., 2014, 56, 159-186. doi: 10.1137/110821871 [14] A. S. Fokas, A unified transform method for solving linear and certain nonlinear PDEs, Proc. Roy. Soc. London A., 1997, 453, 1411-1443. doi: 10.1098/rspa.1997.0077 [15] A. S. Fokas, On the integrability of certain linear and nonlinear partial differential equations, J. Math. Phys., 2000, 41, 4188-4237. doi: 10.1063/1.533339 [16] A. S. Fokas, Two dimensional linear PDEs in a convex polygon, Proc. Roy. Soc. London A., 2001, 457, 371-393. doi: 10.1098/rspa.2000.0671 [17] A. S. Fokas, Integrable nonlinear evolution equations on the half-line, Comm. Math. Phys., 2002, 230, 1-39. doi: 10.1007/s00220-002-0681-8 [18] A. S. Fokas, A new transform method for evolution partial differential equations, IMA J. Appl. Math., 2002, 67, 559-590. doi: 10.1093/imamat/67.6.559 [19] A. S. Fokas, A Unified Approach to Boundary Value Problems, (CBMS-NSF Regional Conference Series in Applied Mathematics) Philadelphia, SIAM., 2008. [20] A. S. Fokas and B. Pelloni, A transform method for linear evolution PDEs on a finite interval, IMA J. Appl. Math., 2005, 70, 564-587. doi: 10.1093/imamat/hxh047 [21] J. S. Pérez Guerrero, E. M. Pontedeiro, M. Th. van Genuchten and T. H. Skaggs, Analytical solution of the one-dimensional advection-dispersion solute transport equation subject to time-dependent boundary conditions, Chem. Eng. J., 2013, 221, 487-491. doi: 10.1016/j.cej.2013.01.095 [22] J. S. Pérez Guerrero, L. C. G. Pimentel, T. H. Skaggs and M. Th. van Genuchten, Analytical solution of the advection-diffusion transport equation using a change-of-variable and integral transform technique, Int. J. Heat Mass Transf., 2009, 52, 3297-3304. doi: 10.1016/j.ijheatmasstransfer.2009.02.002 [23] J. S. Pérez Guerrero, L. C. G. Pimentel, T. H. Skaggs and M. Th. van Genuchten, Analytical solution for multi-species contaminant transport subject to sequential first-order decay reaction in finite media, Transport Porous Med., 2009, 80, 373-357. doi: 10.1007/s11242-009-9368-3 [24] M. T. van Genuchten and W. J. Alves, Analytical solutions of the one-dimensional convective-dispersive solute transport equation, Technical Bulletins 157268, United States Department of Agriculture, Economic Research Service, 1982. [25] G. Hwang, The modified Korteweg-de Vries equation on the quarter plane with t-periodic data, J. Nonlinear Math. Phys., 2017, 24, 620-634. [26] G. Hwang, Initial-boundary value problems for the one-dimensional linear advection-dispersion equation with decay, Z. Naturforshc. A., 2020, 75, 713-725. doi: 10.1515/zna-2020-0106 [27] G. Hwang, A unified approach to two-dimensional linear advection-dispersion equation in cylindrical coordinates on a finite domain, Int. J. Heat Mass Transf., 2021, 164, 120569. doi: 10.1016/j.ijheatmasstransfer.2020.120569 [28] G. Hwang and A. S. Fokas, The modified Korteweg-de Vries equation on the half-line with a sine-wave as Dirichlet datum, J. Nonlinear Math. Phys., 2013, 20, 135-157. [29] D. Mantzavinos and A. S. Fokas, The unified method for the heat equation: I. non-separable boundary conditions and non-local constraints in one dimension, Eur. J. App. Math., 2013, 24, 857-886. doi: 10.1017/S0956792513000223 [30] M. Massabó, R. Cianci and O. Paladino, Some analytical solutions for two-dimensional convection-dispersion equation in cylindrical geometry, Environ. Model. Softw., 2006, 21, 681-688. doi: 10.1016/j.envsoft.2004.12.003 [31] M. Massabó, R. Cianci and O. Paladino, An analytical solution of the advection dispersion equation in a bounded domain and its application to laboratory experiments, J. Appl. Math., 2011, 2011, 493014. [32] P. D. Miller and D. A. Smith, The diffusion equation with nonlocal data, J. Math. Anal. Appl. , 2018, 466, 1119-114. doi: 10.1016/j.jmaa.2018.05.064 [33] A. Mojtabi and M. O. Deville, One-dimensional linear advection-diffusion equation: Analytical and finite element solutions, Comput. Fluids., 2015, 107, 189-195. doi: 10.1016/j.compfluid.2014.11.006 [34] B. Moon and G. Hwang, The Korteweg-de Vries equation on the quarter plane with asymptotically t-periodic data via the Fokas method, Asy. Anal., 2018, 107, 115-133. doi: 10.3233/ASY-171452 [35] B. Moon and G. Hwang, Discrete linear evolution equations in a finite lattice, J. Differ. Equ. Appl., 2019, 25, 630-646. doi: 10.1080/10236198.2019.1613386 [36] A. Moranda, R. Cianci and O. Paladino, Analytical solutions of one-dimensional contaminant transport in soils with source production-decay, Soil Systems, 2018, 2(40), 1-16. [37] K. W. Morton and D. F. Mayers, Numerical Solution of Partial Differential Equations, Cambridge University Press, 2005. [38] B. Pelloni and D. A. Pinotsis, The elliptic sine-Gordon equation in a half plane, Nonlinearity, 2010, 23, 77-88. doi: 10.1088/0951-7715/23/1/004 [39] B. Pelloni and D. A. Smith, Nonlocal and multipoint boundary value problems for linear evolution equations, Stud. Appl. Math., 2018, 141, 46-88. doi: 10.1111/sapm.12212 [40] D. Plümacher, M. Oberlack, Y. Wang and M. Smuda On a non-linear droplet oscillation theory via the unified method, Phys. Fluid., 2020, 32, 067104. doi: 10.1063/5.0007341 [41] N. E. Sheils and B. Deconinck, Heat conduction on the ring: interface problems with periodic boundary conditions, App. Math. Lett., 2014, 37, 107-111. doi: 10.1016/j.aml.2014.06.006 [42] D. Tang, E. O. Frind and E. A. Sudicky, Contaminant transport in fractured porous media: analytical solution for a single fracture, Water Resources Research, 1981, 17, 555-564. doi: 10.1029/WR017i003p00555 -
-
Figures(6)
Export File
Citation
Guenbo Hwang. ANALYTICAL SOLUTION FOR THE TWO-DIMENSIONAL LINEAR ADVECTION-DISPERSION EQUATION IN POROUS MEDIA VIA THE FOKAS METHOD[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2334-2354. doi: 10.11948/20200383
Format
Content
DownLoad:
-
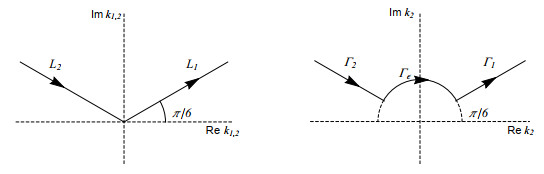
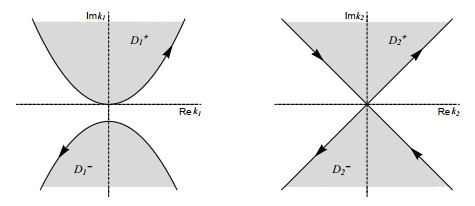
Figure 1. (Left) The region
$ D_1 = D_1^+\cup D_1^- $ (shaded) in the complex$ k_1 $ -plane, where$ {\mathop{{\rm{Re}}}\nolimits} \omega_1(k_1) <0 $ with$ \omega_1(k_1) = b k_1^2+ik_1 $ . (Right) The region$ D_2 = D_2^+\cup D_2^- $ (shaded) in the complex$ k_2 $ -plane, where$ {\mathop{{\rm{Re}}}\nolimits} \omega_2(k_2) <0 $ with$ \omega_2(k_2) = a k_2^2 $ . -
Figure 2. (Left) Efficient contour
$ L = L_1\cup L_2 $ for numerical integration. (Right) Efficient contour$ \Gamma = \Gamma_1\cup \Gamma_2\cup \Gamma_\epsilon $ for numerical integration (see the text for some details). -
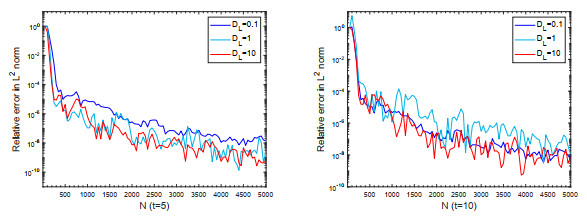
Figure 4. Exponential convergence of the Fokas method for the case of the point pulse initial value. Relative error in the
$ L^2 $ norm versus the number of quadrature points$ N $ when (Left)$ t = 5 $ and (Right)$ t = 10 $ under different dispersion coefficients. -
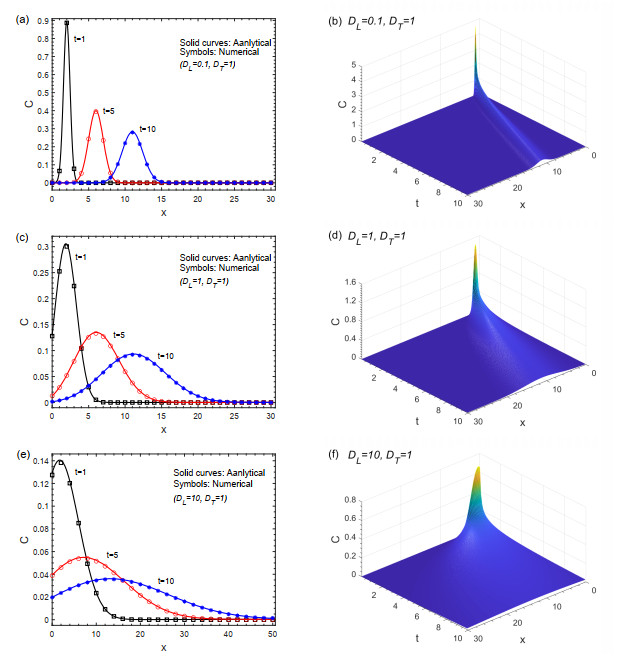
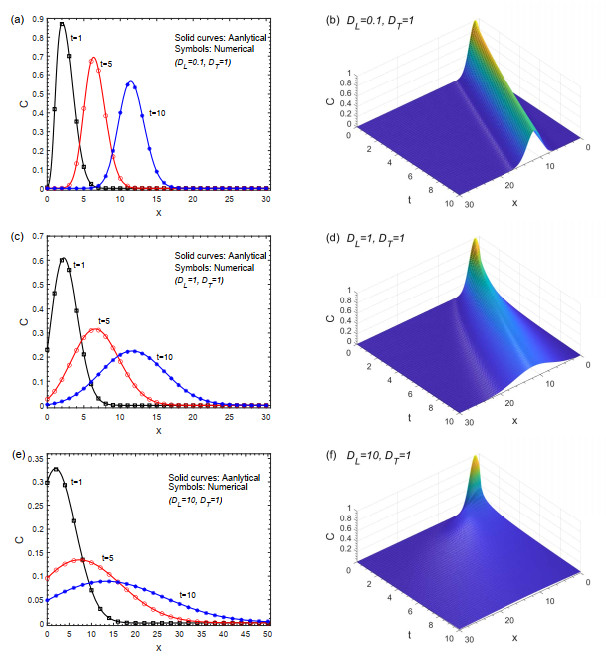
Figure 3. (a, c, e) Comparison of the analytical solutions (solid curves) and the numerical solutions (symbols) with the point pulse initial value in a longitudinal cross-section at
$ y = 0 $ under the different dispersion coefficients. (b, d, f) Analytical solution profiles over the$ xt $ -plane, where$ y = 0 $ under the different dispersion coefficients. -
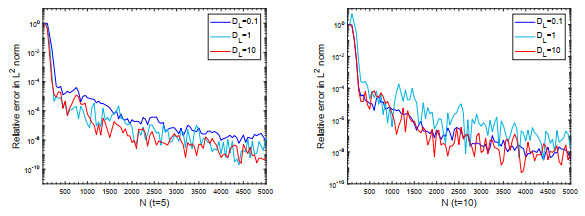
Figure 6. Exponential convergence of the Fokas method for the case of Gaussian initial value. Relative error in the
$ L^2 $ norm versus the number of quadrature points$ N $ when (Left)$ t = 5 $ and (Right)$ t = 10 $ under different dispersion coefficients. -
Figure 5. (a, c, e) Comparison of the analytical solutions (solid curves) and the numerical solutions (symbols) with the Gaussian initial value in a longitudinal cross-section at
$ y = 0 $ under the different dispersion coefficients. (b, d, f) Analytical solution profiles over the$ xt $ -plane, where$ y = 0 $ under the different dispersion coefficients.