Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-28T10:03:14.828Z Has data issue: false hasContentIssue false
  • English
  • Français

On the u∞-torsion submodule of prismatic cohomology

Part of: Discontinuous groups and automorphic forms (Co)homology theory

Published online by Cambridge University Press:  30 June 2023

Shizhang Li  and
Tong Liu
Shizhang Li
Affiliation:
Morningside Center of Mathematics and Hua Loo-Keng Key Laboratory of Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, PR China lishizhang@amss.ac.cn
Tong Liu
Affiliation:
Department of Mathematics, Purdue University, 150 N. University Street, West Lafayette, IN 47907, USA tongliu@purdue.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the maximal finite length submodule of the Breuil–Kisin prismatic cohomology of a smooth proper formal scheme over a 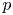$p$-adic ring of integers. This submodule governs pathology phenomena in integral 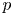$p$-adic cohomology theories. Geometric applications include a control, in low degrees and mild ramifications, of (1) the discrepancy between two naturally associated Albanese varieties in characteristic 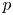$p$, and (2) the kernel of the specialization map in 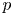$p$-adic étale cohomology. As an arithmetic application, we study the boundary case of the theory due to Fontaine and Laffaille, Fontaine and Messing, and Kato. Also included is an interesting example, generalized from a construction in Bhatt, Morrow and Scholze's work, which illustrates some of our theoretical results being sharp, and negates a question of Breuil.

Keywords

prismatic cohomologycrystalline cohomologyFontaine–Messing theory

MSC classification

Primary: 14F30: $p$-adic cohomology, crystalline cohomology 11F80: Galois representations
Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 8 , August 2023 , pp. 1607 - 1672
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anschütz, J. and Le Bras, A.-C., Prismatic Dieudonné theory, Forum Math. Pi 11 (2023), e2.CrossRefGoogle Scholar
Antieau, B., Bhatt, B. and Mathew, A., Counterexamples to Hochschild–Kostant–Rosenberg in characteristic $p$, Forum Math. Sigma 9 (2021), e49; MR 4277271.CrossRefGoogle Scholar
Antieau, B., Mathew, A., Morrow, M. and Nikolaus, T., On the Beilinson fiber square, Duke Math. J. 171 (2022), 3707–3806; MR 4516307.CrossRefGoogle Scholar
Berthelot, P., Breen, L. and Messing, W., Théorie de Dieudonné cristalline. II, Lecture Notes in Mathematics, vol. 930 (Springer, Berlin, 1982); MR 667344.CrossRefGoogle Scholar
Bhatt, B. and de Jong, A. J., Crystalline cohomology and de Rham cohomology, Preprint (2011), arXiv:1110.5001.Google Scholar
Bhatt, B. and Lurie, J., Absolute prismatic cohomology, Preprint (2022), arXiv:2201.06120.Google Scholar
Bhatt, B. and Mathew, A., The arc-topology, Duke Math. J. 170 (2021), 1899–1988; MR 4278670.CrossRefGoogle Scholar
Bhatt, B., Morrow, M. and Scholze, P., Integral $p$-adic Hodge theory, Publ. Math. Inst. Hautes Études Sci. 128 (2018), 219–397; MR 3905467.CrossRefGoogle Scholar
Bhatt, B., Morrow, M. and Scholze, P., Topological Hochschild homology and integral $p$-adic Hodge theory, Publ. Math. Inst. Hautes Études Sci. 129 (2019), 199–310; MR 3949030.CrossRefGoogle Scholar
Bhatt, B. and Scholze, P., Prismatic $F$-crystals and crystalline galois representations, Preprint (2021), arXiv:2106.14735.Google Scholar
Bhatt, B. and Scholze, P., Prisms and prismatic cohomology, Ann. of Math. (2) 196 (2022), 1135–1275; MR 4502597.CrossRefGoogle Scholar
Bondarko, M. V., The generic fiber of finite group schemes; a “finite wild” criterion for good reduction of abelian varieties, Izv. Ross. Akad. Nauk Ser. Mat. 70 (2006), 21–52; MR 2261169.Google Scholar
Bosch, S., Lectures on formal and rigid geometry, Lecture Notes in Mathematics, vol. 2105 (Springer, Cham, 2014); MR 3309387.CrossRefGoogle Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedean analysis: A systematic approach to rigid analytic geometry, Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 261 (Springer, Berlin, 1984); MR 746961.CrossRefGoogle Scholar
Breuil, C., Cohomologie étale de $p$-torsion et cohomologie cristalline en réduction semi-stable, Duke Math. J. 95 (1998), 523–620; MR 1658764.CrossRefGoogle Scholar
Breuil, C., Integral p-adic Hodge theory, in Algebraic geometry 2000, Azumino (Hotaka), Advanced Studies in Pure Mathematics., vol. 36 (The Mathematical Society of Japan, Tokyo, 2002), 51–80; MR 1971512 (2004e:11135).Google Scholar
Caruso, X., Conjecture de l'inertie modérée de Serre, Invent. Math. 171 (2008), 629–699; MR 2372809 (2008j:14034).CrossRefGoogle Scholar
Chambert-Loir, A., Cohomologie cristalline: un survol, Expo. Math. 16 (1998), 333–382; MR 1654786.Google Scholar
Faltings, G., Integral crystalline cohomology over very ramified valuation rings, J. Amer. Math. Soc. 12 (1999), 117–144; MR 1618483 (99e:14022).CrossRefGoogle Scholar
Farb, B., Kisin, M. and Wolfson, J., Essential dimension via prismatic cohomology, Preprint (2021), arXiv:2110.05534.Google Scholar
Fontaine, J.-M., Représentations p-adiques des corps locaux. I, in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, vol. 87 (Birkhäuser, Boston, MA, 1990), 249–309; MR 1106901 (92i:11125).Google Scholar
Fontaine, J.-M. and Laffaille, G., Construction de représentations $p$-adiques, Ann. Sci. Éc. Norm. Supér. (4) 15 (1982), 547–608 (fr); MR 85c:14028.CrossRefGoogle Scholar
Fontaine, J.-M. and Messing, W., p-adic periods and p-adic étale cohomology, in Current trends in arithmetical algebraic geometry (Arcata, Calif., 1985), Contemporary Mathematics, vol. 67 (American Mathematical Society, Providence, RI, 1987), 179–207; MR 902593 (89g:14009).Google Scholar
Gao, H., Galois lattices and strongly divisible lattices in the unipotent case, J. Reine Angew. Math. 728 (2017), 263–299; MR 3668997.CrossRefGoogle Scholar
Hansen, D. and Li, S., Line bundles on rigid varieties and Hodge symmetry, Math. Z. 296 (2020), 1777–1786; MR 4159850.CrossRefGoogle Scholar
Hartl, U. and Lütkebohmert, W., On rigid-analytic Picard varieties, J. Reine Angew. Math. 528 (2000), 101–148; MR 1801659.Google Scholar
Illusie, L., Complexe de de Rham–Witt et cohomologie cristalline, Ann. Sci. Éc. Norm. Supér. (4) 12 (1979), 501–661; MR 565469.CrossRefGoogle Scholar
Kato, K., On p-adic vanishing cycles (application of ideas of Fontaine-Messing), in Algebraic geometry, Sendai, 1985, Advanced Studies in Pure Mathematics, vol. 10 (North-Holland, Amsterdam, 1987), 207–251; MR 946241.Google Scholar
Katz, N. M., p-adic properties of modular schemes and modular forms, in Modular functions of one variable, III (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Math., vol. 350 (Springer, Berlin, 1973), 69–190; MR 0447119.Google Scholar
Kisin, M., Crystalline representations and F-crystals, in Algebraic geometry and number theory, Progress in Mathematics, vol. 253 (Birkhäuser, Boston, MA, 2006), 459–496; MR2263197 (2007j:11163).Google Scholar
Kisin, M., Moduli of finite flat group schemes, and modularity, Ann. of Math. (2) 170 (2009), 1085–1180; MR 2600871.CrossRefGoogle Scholar
Knudsen, F. F. and Mumford, D., The projectivity of the moduli space of stable curves. I. Preliminaries on “det” and “Div”, Math. Scand. 39 (1976), 19–55; MR 437541.CrossRefGoogle Scholar
Kubrak, D. and Prikhodko, A., $p$-adic Hodge theory for Artin stacks, Mem. Amer. Math. Soc., to appear. Preprint (2021), arXiv:2105.05319.Google Scholar
Li, S., Integral $p$-adic Hodge filtrations in low dimension and ramification, J. Eur. Math. Soc. (JEMS) 24 (2022), 3801–3827; MR 4493614.CrossRefGoogle Scholar
Liu, T., A note on lattices in semi-stable representations, Math. Ann. 346 (2010), 117–138; MR 2558890.CrossRefGoogle Scholar
Li, S. and Liu, T., Comparison of prismatic cohomology and derived de Rham cohomology, J. Eur. Math. Soc. (JEMS), to appear. Preprint (2020), arXiv:2012.14064.Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009); MR 2522659.CrossRefGoogle Scholar
Lütkebohmert, W., The structure of proper rigid groups, J. Reine Angew. Math. 468 (1995), 167–219; MR 1361790.Google Scholar
Min, Y., Integral $p$-adic Hodge theory of formal schemes in low ramification, Algebra Number Theory 15 (2021), 1043–1076; MR 4265353.CrossRefGoogle Scholar
Mondal, S., Dieudonné theory via cohomology of classifying stacks, Forum Math. Sigma 9 (2021), e81; MR 4354128.CrossRefGoogle Scholar
Raynaud, M., Schémas en groupes de type $(p,\ldots, p)$, Bull. Soc. Math. France 102 (1974), 241–280; MR 419467.CrossRefGoogle Scholar
Raynaud, M., “p-torsion” du schéma de Picard, in Journées de Géométrie Algébrique de Rennes (Rennes, 1978), Vol. II, Astérisque, vol. 64 (Société Mathématique de France, Paris, 1979), 87–148; MR 563468.Google Scholar
Serre, J.-P. and Tate, J., Good reduction of abelian varieties, Ann. of Math. (2) 88 (1968), 492–517; MR 236190.CrossRefGoogle Scholar
The Stacks project authors, The stacks project (2021), https://stacks.math.columbia.edu.Google Scholar
Vasiu, A. and Zink, T., Boundedness results for finite flat group schemes over discrete valuation rings of mixed characteristic, J. Number Theory 132 (2012), 2003–2019; MR 2925859.CrossRefGoogle Scholar
Wintenberger, J.-P., Un scindage de la filtration de Hodge pour certaines variétés algébriques sur les corps locaux, Ann. of Math. (2) 119 (1984), 511–548; MR 744862.CrossRefGoogle Scholar