Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-28T17:00:37.964Z Has data issue: false hasContentIssue false
  • English
  • Français

Skew group categories, algebras associated to Cartan matrices and folding of root lattices

Part of: Rings and algebras arising under various constructions Lie algebras and Lie superalgebras Representation theory of rings and algebras Modules, bimodules and ideals

Published online by Cambridge University Press:  01 April 2024

Xiao-Wu Chen  and
Ren Wang
Xiao-Wu Chen
Affiliation:
Key Laboratory of Wu Wen-Tsun Mathematics, Chinese Academy of Sciences, School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, Anhui, PR China (xwchen@mail.ustc.edu.cn)
Ren Wang
Affiliation:
School of Mathematics, Hefei University of Technology, Hefei 230000, Anhui, PR China (renw@mail.ustc.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

For an action of a finite group on a finite EI quiver, we construct its ‘orbifold’ quotient EI quiver. The free EI category associated to the quotient EI quiver is equivalent to the skew group category with respect to the given group action. Specializing the result to a finite group action on a finite acyclic quiver, we prove that, under reasonable conditions, the skew group category of the path category is equivalent to a finite EI category of Cartan type. If the ground field is of characteristic $p$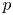 and the acting group is a cyclic $p$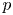-group, we prove that the skew group algebra of the path algebra is Morita equivalent to the algebra associated to a Cartan matrix, defined in [C. Geiss, B. Leclerc, and J. Schröer, Quivers with relations for symmetrizable Cartan matrices I: Foundations, Invent. Math. 209 (2017), 61–158]. We apply the Morita equivalence to construct a categorification of the folding projection between the root lattices with respect to a graph automorphism. In the Dynkin cases, the restriction of the categorification to indecomposable modules corresponds to the folding of positive roots.

Keywords

FoldingCartan matrixgraph with automorphismfree EI categoryskew group category

MSC classification

Primary: 16G20: Representations of quivers and partially ordered sets
Secondary: 16S35: Twisted and skew group rings, crossed products 16D90: Module categories ; module theory in a category-theoretic context; Morita equivalence and duality 17B22: Root systems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 45
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, M., Reiten, I. and Smalø, S. O., Representation Theory of Artin Algebras, Cambridge Studies in Adv. Math. Vol. 36 (Cambridge Univ. Press, Cambridge, 1995).CrossRefGoogle Scholar
Bass, H.. Covering theory for graphs of groups. J. Pure Appl. Algebra 89 (1993), 3–47.CrossRefGoogle Scholar
Chen, X. W.. Equivariantization and Serre duality I. Appl. Categor. Struct. 25 (2017), 539–568.CrossRefGoogle Scholar
Chen, X. W. and Wang, R.. The finite EI categories of Cartan type. J. Algebra 546 (2020), 62–84.CrossRefGoogle Scholar
Cibils, C. and Marcos, E. N.. Skew category, Galois covering and smash product of a $k$-category. Proc. Amer. Math. Soc. 134 (2005), 39–50.CrossRefGoogle Scholar
Deng, B. and Du, J.. Frobenius morphisms and representations of algebras. Trans. Amer. Math. Soc. 358 (2006), 3591–3622.CrossRefGoogle Scholar
Deng, B. and Xiao, J.. A new approach to Kac's theorem on representations of valued quivers. Math. Z. 245 (2003), 183–199.CrossRefGoogle Scholar
Dlab, V. and Ringel, C. M., Indecomposable representations of graphs and algebras, Mem. Amer. Math. Soc., Vol. 173 (American Mathematical Society, Providence, RI, 1976).CrossRefGoogle Scholar
Gabriel, P.. Unzerlegbare Darstellungen I. Math. Manu. 6 (1972), 71–103.CrossRefGoogle Scholar
Geiss, C., Quiver with relations for symmetrizable Catan matrices and algebraic Lie theory, Proc. Int. Cong. Math., Rio de Janeiro, Vol. 2 (2018), pp. 99–124 (World Scientific Publishing, Singapore, 2018).CrossRefGoogle Scholar
Geiss, C., Leclerc, B. and Schröer, J.. Quivers with relations for symmetrizable Cartan matrices I: foundations. Invent. Math. 209 (2017), 61–158.CrossRefGoogle Scholar
Geiss, C., Leclerc, B. and Schröer, J.. Quivers with relations for symmetrizable Cartan matrices II: Change of symmetrizer. Int. Math. Res. Not. IMRN 9 (2018), 2866–2898.Google Scholar
Geiss, C., Leclerc, B. and Schröer, J.. Rigid modules and Schur roots. Math. Z. 295 (2020), 1245–1277.CrossRefGoogle Scholar
Giovannini, S. and Pasquali, A.. Skew group algebras of Jacobian algebras. J. Algebra 526 (2019), 112–165.CrossRefGoogle Scholar
Grothendieck, A., Revêtements étales et groupe fondamental (SGA 1), Seminaire de Geometrie Algebrique 1960/61 (Institut des Hautes Études Scientifiques, Paris, 1963).Google Scholar
Huang, H. L., Lin, Z. and Su, X.. The Auslander–Reiten quivers of string algebras of type $\tilde {C}_n-1$ and a conjecture by Geiss–Leclerc–Schröer. J. Algebra 632 (2023), 331–362.CrossRefGoogle Scholar
Hubery, A.. Quiver representations respecting a quiver automorphism: a generalisation of a theorem of Kac. J. London Math. Soc. 69 (2004), 79–96.CrossRefGoogle Scholar
Kac, V.. Infinite root systems, representations of graphs and invariant theory. Invent. Math. 56 (1980), 57–92.CrossRefGoogle Scholar
Kac, V.. Infinite Dimensional Lie Algebras, 3rd Ed. (Cambridge Univ. Press, Cambridge, 1990).CrossRefGoogle Scholar
Le Meur, P.. Crossed products of Calabi–Yau algebras by finite groups. J. Pure Appl. Algebra 224 (2020), 106394.CrossRefGoogle Scholar
Li, L.. A characterization of finite EI categories with hereditary category algebras. J. Algebra 345 (2011), 213–241.CrossRefGoogle Scholar
Linckelmann, M.. A version of Alperin's weight conjecture for finite category algebras. J. Algebra 398 (2014), 386–395.CrossRefGoogle Scholar
Lusztig, G., Introduction to Quantum Groups, Progress in Math. Vol. 110 (Birkhäuser, Boston Basel Berlin, 1993).Google Scholar
Lück, W., Transformation Groups and Algebraic K-Theory, Lecture Notes Math. Vol. 1408 (Springer-Verlag, Heidelberg, 1989).CrossRefGoogle Scholar
Nastasescu, C. and Van Oystaeyen, F., Methods of Graded Rings, Lecture Notes Math. Vol. 1836 (Springer-Verlag, Berlin Heidelberg, 2004).CrossRefGoogle Scholar
Reiten, I. and Riedtmann, Ch.. Skew group algebras in the representation theory of artin algebras. J. Algebra 92 (1985), 224–282.CrossRefGoogle Scholar
Serre, J. P.. Trees, Translated from the French by John Stillwell (Springer-Verlag, Berlin Heidelberg New York, 1980).Google Scholar
Springer, T. A., Linear Algebraic Groups, 2nd Ed., Progress in Math. Vol. 9 (Birkhäuser, Boston Basel Berlin, 1998).CrossRefGoogle Scholar
Steinberg, R.. Lectures on Chevalley Groups (Yale University, New Haven, 1967).Google Scholar
Tanisaki, T.. Foldings of root systems and Gabriel's theorem. Tsukuba J. Math. 4 (1980), 89–97.CrossRefGoogle Scholar
Wang, R.. Gorenstein triangular matrix rings and category algebras. J. Pure Appl. Algebra 220 (2016), 666–682.CrossRefGoogle Scholar
Webb, P., An introduction to the representations and cohomology of categories, in: Group Representation Theory (EPFL Press, Lausanne, 2007), pp. 149–173.Google Scholar
Webb, P.. Standard stratifications of EI categories and Alperin's weight conjecture. J. Algebra 320 (2008), 4073–4091.CrossRefGoogle Scholar
Wemyss, M., Lectures on noncommutative resolutions, in Noncommutative Algebraic Geometry, 239–306, Math. Sci. Res. Inst. Publ. Vol. 64 (Cambridge Univ. Press, New York, 2016).Google Scholar
Xu, F.. On local categories of finite groups. Math. Z. 272 (2012), 1023–1036.CrossRefGoogle Scholar
Xu, F.. Support varieties for transporter category algebras. J. Pure Appl. Algebra 218 (2014), 583–601.CrossRefGoogle Scholar