Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-28T10:53:35.024Z Has data issue: false hasContentIssue false
  • English
  • Français

Resolving an old problem on the preservation of the IFR property under the formation of 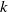$k$-out-of-$n$ systems with discrete distributions

Part of: Survival analysis and censored data

Published online by Cambridge University Press:  16 October 2023

Mahdi Alimohammadi Open the ORCID record for Mahdi Alimohammadi [Opens in a new window]  and
Jorge Navarro Open the ORCID record for Jorge Navarro [Opens in a new window]
Mahdi Alimohammadi*
Affiliation:
Alzahra University
Jorge Navarro*
Affiliation:
Universidad de Murcia
*
*Postal address: Department of Statistics, Faculty of Mathematical Sciences, Alzahra University, Tehran, Iran. Email address: m.alimohammadi@alzahra.ac.ir
**Postal address: Department of Statistics and Operation Research, Universidad de Murcia, 30100 Murcia, Spain. Email address: jorgenav@um.es
Get access Rights & Permissions [Opens in a new window]

Abstract

More than half a century ago, it was proved that the increasing failure rate (IFR) property is preserved under the formation of k-out-of-n systems (order statistics) when the lifetimes of the components are independent and have a common absolutely continuous distribution function. However, this property has not yet been proved in the discrete case. Here we give a proof based on the log-concavity property of the function 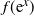$f({{\mathrm{e}}}^x)$. Furthermore, we extend this property to general distribution functions and general coherent systems under some conditions.

Keywords

Coherent systemsageing classesfailure ratelog-concavityorder statistics

MSC classification

Secondary: 62N05: Reliability and life testing
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abouammoh, A. and El-Neweihi, E. (1986). Closure of NBUE and DMRL under the formation of parallel systems. Statist. Prob. Lett. 4, 223–225.CrossRefGoogle Scholar
Alimohammadi, M., Alamatsaz, M. H. and Cramer, E. (2015). Discrete strong unimodality of order statistics. Statist. Prob. Lett. 103, 176–185.CrossRefGoogle Scholar
An, M. Y. (1998). Logconcavity versus logconvexity: a complete characterization. J. Econom. Theory 80, 350–369.CrossRefGoogle Scholar
Arnold, B. C., Balakrishnan, N. and Nagaraja, H. N. (2008). A First Course in Order Statistics, 2nd edn. John Wiley, New York.CrossRefGoogle Scholar
Barlow, R. E. and Proschan, F. (1975). Statistical Theory of Reliability and Life Testing. Holt, Rinehart & Winston, New York.Google Scholar
Block, H. W. and Savits, T. H. (1976). The IFRA closure problem. Ann. Prob. 4, 1030–1032.CrossRefGoogle Scholar
Bracquemond, C., Gaudoin, O., Roy, D. and Xie, M. (2001). On some discrete notions of aging. In System and Bayesian Reliability: Essays in Honor of Professor Richard E. Barlow on His 70th Birthday, ed. Y. Hayakawa et al., pp. 185–197. World Scientific.CrossRefGoogle Scholar
Dembińska, A. (2008). Discrete order statistics. In Encyclopedia of Statistical Sciences, ed. S. Kotz et al. John Wiley, Hoboken, NJ.CrossRefGoogle Scholar
Esary, J. and Proschan, F. (1963). Relationship between system failure rate and component failure rates. Technometrics 5, 183–189.CrossRefGoogle Scholar
Esary, J. D., Marshall, A. W. and Proschan, F. (1970). Some reliability applications of the hazard transform. SIAM J. Appl. Math. 18, 849–860.CrossRefGoogle Scholar
Gupta, P. L., Gupta, R. C. and Tripathi, R. C. (1997). On the monotone properties of discrete failure rates. J. Statist. Planning Infer. 65, 255–268.CrossRefGoogle Scholar
Hu, T., Nanda, A. K., Xie, H. and Zhu, Z. (2004). Properties of some stochastic orders: a unified study. Naval Res. Logistics 51, 193–216.CrossRefGoogle Scholar
Johnson, N. L., Kemp, A. W. and Kotz, S. (2005). Univariate Discrete Distributions, 3rd edn. John Wiley, New York.CrossRefGoogle Scholar
Kemp, A. W. (2004). Classes of discrete life distributions. Commun. Statist. Theory Meth. 33, 3069–3093.CrossRefGoogle Scholar
Li, C. and Li, X. (2020). Weak aging properties for coherent systems with statistically dependent component lifetimes. Naval Res. Logistics 67, 559–572.CrossRefGoogle Scholar
Lindqvist, B. H. and Samaniego, F. J. (2019). Some new results on the preservation of the NBUE and NWUE aging classes under the formation of coherent systems. Naval Res. Logistics 66, 430–438.CrossRefGoogle Scholar
Lindqvist, B. H., Samaniego, F. J. and Huseby, A. B. (2016). On the equivalence of systems of different sizes, with applications to system comparisons. Adv. Appl. Prob. 48, 332–348.CrossRefGoogle Scholar
Marshall, A. W. and Olkin, I. (2007). Life Distributions. Springer, New York.Google Scholar
Navarro, J. (2018). Preservation of DMRL and IMRL aging classes under the formation of order statistics and coherent systems. Statist. Prob. Lett. 137, 264–268.CrossRefGoogle Scholar
Navarro, J. (2022). Introduction to System Reliability Theory. Springer.CrossRefGoogle Scholar
Navarro, J., del Águila, Y., Sordo, M. A. and Suárez-Llorens, A. (2014). Preservation of reliability classes under the formation of coherent systems. Appl. Stoch. Models Business Industry 30, 444–454.CrossRefGoogle Scholar
Roberts, A. W. and Varberg, D. E. (1973). Convex Functions. Academic Press, New York and London.Google Scholar
Roy, D. and Gupta, R. P. (1992). Classifications of discrete lives. Microelectron. Reliab. 32, 1459–1473.CrossRefGoogle Scholar
Rychlik, T. and Szymkowiak, M. (2021). Properties of system lifetime in the classical model with I.I.D. exponential component lifetimes. In Advances in Statistics: Theory and Applications, ed. I. Ghosh et al., pp. 43–66. Springer.Google Scholar
Samaniego, F. J. (1985). On closure of the IFR class under formation of coherent systems. IEEE Trans. Reliab. R-34, 69–72.CrossRefGoogle Scholar
Shaked, M. and Shanthikumar, J. G. (2007). Stochastic Orders. Springer, New York.CrossRefGoogle Scholar