Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-28T16:10:26.643Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-normalized Cramér moderate deviations for a supercritical Galton–Watson process

Part of: Parametric inference Limit theorems Markov processes

Published online by Cambridge University Press:  24 April 2023

Xiequan Fan  and
Qi-Man Shao
Xiequan Fan*
Affiliation:
Northeastern University at Qinhuangdao
Qi-Man Shao*
Affiliation:
Southern University of Science and Technology
*
*Postal address: School of Mathematics and Statistics, Northeastern University at Qinhuangdao, Qinhuangdao, 066004, Hebei, China. Email address: fanxiequan@hotmail.com
**Postal address: Department of Statistics and Data Science, SICM, National Center for Applied Mathematics Shenzhen, Southern University of Science and Technology, Shenzhen 518055, Guangdong, China. Email address: shaoqm@sustech.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 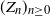$(Z_n)_{n\geq0}$ be a supercritical Galton–Watson process. Consider the Lotka–Nagaev estimator for the offspring mean. In this paper we establish self-normalized Cramér-type moderate deviations and Berry–Esseen bounds for the Lotka–Nagaev estimator. The results are believed to be optimal or near-optimal.

Keywords

Self-normalized processesLotka–Nagaev estimatorBerry–Esseen boundsoffspring mean

MSC classification

Primary: 60F10: Large deviations 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 62F12: Asymptotic properties of estimators 62F03: Hypothesis testing
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 4 , December 2023 , pp. 1281 - 1292
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. B. (1994). Large deviation rates for branching processes I: Single type case. Ann. Appl. Prob. 4, 779–790.CrossRefGoogle Scholar
Bercu, B. and Touati, A. (2008). Exponential inequalities for self-normalized martingales with applications. Ann. Appl. Prob. 18, 1848–1869.CrossRefGoogle Scholar
Chu, W. (2018). Self-normalized large deviation for supercritical branching processes. J. Appl. Prob. 55, 450–458.Google Scholar
De la Peña, V. H., Lai, T. L. and Shao, Q. M. (2009). Self-Normalized Processes, Limit Theorems and Statistical Applications. Springer.Google Scholar
Fan, X. (2019). Exact rates of convergence in some martingale central limit theorems. J. Math. Anal. Appl. 469, 1028–1044.CrossRefGoogle Scholar
Fan, X. and Shao, Q. M. (2018). Berry–Esseen bounds for self-normalized martingales. Commun. Math. Statist. 6, 13–27.CrossRefGoogle Scholar
Fan, X., Grama, I., Liu, Q. and Shao, Q. M. (2019). Self-normalized Cramér type moderate deviations for martingales. Bernoulli 25, 2793–2823.CrossRefGoogle Scholar
Fan, X., Grama, I., Liu, Q. and Shao, Q. M. (2020). Self-normalized Cramér type moderate deviations for stationary sequences and applications. Stoch. Process. Appl. 130, 5124–5148.CrossRefGoogle Scholar
He, H. (2016). On large deviation rates for sums associated with Galton–Watson processes. Adv. Appl. Prob. 48, 672–690.CrossRefGoogle Scholar
Jing, B. Y., Shao, Q. M. and Wang, Q. (2003). Self-normalized Cramér-type large deviations for independent random variables. Ann. Prob. 31, 2167–2215.CrossRefGoogle Scholar
Kuelbs, J. and Vidyashankar, A. N. (2011). Weak convergence results for multiple generations of a branching process. J. Theor. Prob. 24, 376–396.CrossRefGoogle Scholar
Lotka, A. (1939). Théorie analytique des associations biologiques. Actualités Sci. Ind. 780, 123–136.Google Scholar
Maaouia, F. and Touati, A. (2005). Identification of multitype branching processes. Ann. Statist. 33, 2655–2694.CrossRefGoogle Scholar
Nagaev, S. V. (1967). On estimating the expected number of direct descendants of a particle in a branching process. Theory Prob. Appl. 12, 314–320.CrossRefGoogle Scholar
Ney, P. E. and Vidyashankar, A. N. (2003). Harmonic moments and large deviation rates for supercritical branching processes. Ann. Appl. Prob. 13, 475–489.CrossRefGoogle Scholar
Ney, P. E. and Vidyashankar, A. N. (2004). Local limit theory and large deviations for supercritical branching processes. Ann. Appl. Prob. 14, 1135–1166.CrossRefGoogle Scholar