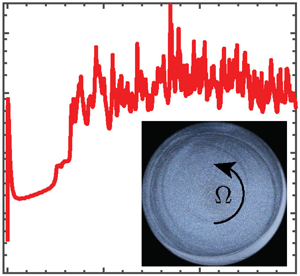
It is well known that inertia-free shearing flows of a viscoelastic fluid with curved streamlines, such as the torsional flow between a rotating cone and plate or the flow in a Taylor–Couette geometry, can become unstable to a three-dimensional time-dependent instability at conditions exceeding a critical Weissenberg ($Wi$) number. However, the combined effects of fluid elasticity, shear thinning and finite inertia (as quantified by the Reynolds number $Re$) on the onset of elasto-inertial instabilities are not fully understood. Using a set of cone–plate geometries, we experimentally explore the entire $Wi$–$Re$ phase space for a series of nonlinear viscoelastic fluids (with the dependence on shear rate $\dot{\gamma}$ quantified using a shear-thinning parameter $\beta _P(\dot {\gamma })$). We tune $\beta _P(\dot {\gamma })$ by varying the dissolved polymer concentration in solution. This progressively reduces shear thinning but leads to finite inertial effects before the onset of elastic instability, and thus naturally results in elasto-inertial coupling. Time-resolved rheometric measurements and flow visualization experiments allow us to investigate the effects of flow geometry, and document the combined effects of varying $Wi, Re$ and $\beta _P(\dot {\gamma })$ on the emergence of secondary motions at the onset of instability. The resulting critical state diagram quantitatively depicts the competition between the stabilizing effects of shear thinning and the destabilizing effects of inertia. We extend the curved streamline instability criterion of Pakdel & McKinley (Phys. Rev. Lett., vol. 77, no. 12, 1996, p. 2459) for the onset of purely elastic instability in curvilinear geometries by using scaling arguments to incorporate shear thinning and finite inertial effects. The augmented condition facilitates predictions of the onset of instability over a broader range of flow conditions, and thus bridges the gap between purely elastic and elasto-inertial curved streamline instabilities.