Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-25T18:37:09.437Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities and representation formulas for functions of exponential type

Part of: Harmonic analysis in one variable Entire and meromorphic functions, and related topics Approximations and expansions

Published online by Cambridge University Press:  09 April 2009

C. Frappier  and
P. Olivier
C. Frappier
Affiliation:
Départment de Mathématiques Appliquées, École Polytechnique de Montréal, Campus de l'Université de MontréalC.P. 6079, Succursale Centre-ville, Montréal (Québec) H3C 3A7, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We generalise the classical Bernstein's inequality: 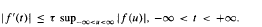. Moreover we obtain a new representation formula for entire functions of exponential type.

Keywords

Bernstein's inequalityentire functionsinterpolation pointsapproximation.

MSC classification

Secondary: 41A05: Interpolation 41A17: Inequalities in approximation (Bernstein, Jackson, Nikol'skiĭ-type inequalities) 30D10: Representations of entire functions by series and integrals 42A05: Trigonometric polynomials, inequalities, extremal problems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 58 , Issue 1 , February 1995 , pp. 15 - 26
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Achieser, N. I., Theory of approximation (Frederick Ungar Publishing Co., New York, 1956).Google Scholar
[2]Boas, R. P., Entire functions (Academic Press, New York, 1954).Google Scholar
[3]Frappier, C., ‘Representation formulas for integrable and entire functions of exponential type I’, Canad. J. Math. 40 (1988), 1010–1024.CrossRefGoogle Scholar
[4]Frappier, C., ‘Representation formulas for integrable and entire functions of exponential type II’, Canad. J. Math. 43 (1991), 1–14.CrossRefGoogle Scholar
[5]Hörmander, L., ‘Some inequalities for functions of exponential type’, Math. Scand. 3 (1955), 21–27.CrossRefGoogle Scholar
[6]Lewitan, B. M., ‘Über eine verallgemeinerung der ungleichunger von S. Bernstein und H. Bohr’, Dokl. Akad. Nauk SSSR 15 (1937), 169–172.Google Scholar
[7]McNamee, J., Stenger, F. and Whitney, E. L., ‘Whittaker's cardinal function in retrospect’, Math. Comp. 25 (1971), 141–154.Google Scholar
[8]Rahman, Q. I., ‘On asymmetric entire functions II’, Math. Ann. 167 (1966), 49–52.CrossRefGoogle Scholar
[9]Valiron, G., ‘Sur la formule d'interpolation de Lagrange’, Bull. Sci. Math. (2) 49 (1925), 181–192, 203–224.Google Scholar