No CrossRef data available.
Article contents
Compactifications of discrete versions of semitopological semigroups by filters of zero sets
Published online by Cambridge University Press: 24 October 2008
Abstract
The maximal proper prime filters together with the ultrafilters of zero sets of any metrizable compact topological space are shown to have a compact Hausdorff topology in which the ultrafilters form a discrete, dense subspace. This gives a general theory of compactifications of discrete versions of compact metrizable topological spaces and some of the already known constructions of compact right topological semigroups are special cases of the general theory. In this way, simpler and more elegant proofs for these constructions are obtained.
In [8], Pym constructed compactifications for discrete semigroups which can be densely embedded in a compact group. His techniques made extensive use of function algebras. In [4] Helmer and Isik obtained the same compactifications by using the existence of Stone  ech compactifications. The aim of this paper is to present a general theory of compactifications of semitopological semigroups so that Helmer and Isik's results in [4] are a simple consequence. Our proofs are different and are based on filters which provide a natural way of getting compactifications. Moreover we present new insights by emphasizing maximal proper primes which are not ultrafilters.
ech compactifications. The aim of this paper is to present a general theory of compactifications of semitopological semigroups so that Helmer and Isik's results in [4] are a simple consequence. Our proofs are different and are based on filters which provide a natural way of getting compactifications. Moreover we present new insights by emphasizing maximal proper primes which are not ultrafilters.
We start by defining filters of zero sets (called z-filters) on a given topological space X, and their convergence. In the case of compact metrizable topological spaces, we establish the connections between proper maximal prime z-filters on X and zultrafilters in β(X\{x})\(X\{x}) where β(X\{x}) is the Stone- ech compactification of X\{x}. We then define a topology on the set of all prime z-filters on X such that the subspace of all proper maximal primes is compact Hausdorff. We denote by
ech compactification of X\{x}. We then define a topology on the set of all prime z-filters on X such that the subspace of all proper maximal primes is compact Hausdorff. We denote by 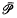 the set of all proper maximal prime z-filters on X together with the z-ultrafilters and show that when X is a compact metrizable cancellative semitopological semigroup,
the set of all proper maximal prime z-filters on X together with the z-ultrafilters and show that when X is a compact metrizable cancellative semitopological semigroup, 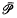 is a compact right topological semigroup with dense topological centre. Also, when
is a compact right topological semigroup with dense topological centre. Also, when 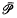 is considered for a compact Hausdorff metrizable group, the semigroup obtained is exactly the same (algebraically and topologically) as the semigroup obtained in [4]. Hence the result in [4] is just a consequence of the general theory presented in this paper.
is considered for a compact Hausdorff metrizable group, the semigroup obtained is exactly the same (algebraically and topologically) as the semigroup obtained in [4]. Hence the result in [4] is just a consequence of the general theory presented in this paper.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 2 , March 1991 , pp. 363 - 373
- Copyright
- Copyright © Cambridge Philosophical Society 1991




