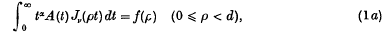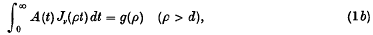Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Williams, W. E.
1963.
A class of integral equations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 59,
Issue. 3,
p.
589.
Cooke, J. C.
1963.
Some Further Triple Integral Equation Solutions.
Proceedings of the Edinburgh Mathematical Society,
Vol. 13,
Issue. 4,
p.
303.
Fox, Charles
1965.
A formal solution of certain dual integral equations.
Transactions of the American Mathematical Society,
Vol. 119,
Issue. 3,
p.
389.
Robertson, Ian A.
1966.
Forced vertical vibration of a rigid circular disc on a semi-infinite elastic solid.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 62,
Issue. 3,
p.
547.
Robertson, Ian A.
1967.
On a proposed determination of the shear modulus of an isotropic elastic half-space by the forced torsional oscillations of a circular disc.
Applied Scientific Research,
Vol. 17,
Issue. 4-5,
p.
305.
Robertson, Ian A.
1967.
Diffraction of a plane longitudinal wave by a penny-shaped crack.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 63,
Issue. 1,
p.
229.
Paul, H. S.
1969.
Longitudinal wave propagation in an infinite isotropic elastic plate with a penny-shaped crack.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 66,
Issue. 2,
p.
439.
Linz, Peter
1969.
The numerical solution of certain dual integral equations.
Journal of Engineering Mathematics,
Vol. 3,
Issue. 3,
p.
245.
1969.
The theory of absolute surface shear viscosity. I.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 310,
Issue. 1502,
p.
359.
Jain, D. L.
and
Kanwal, R. P.
1970.
Acoustic diffraction by a rigid annular disk.
Journal of Engineering Mathematics,
Vol. 4,
Issue. 3,
p.
219.
Andreikiv, A. E.
and
Panasyuk, V. V.
1970.
The elastic equilibrium of an unbounded body, weakened by a system of concentric cracks.
Soviet Applied Mechanics,
Vol. 6,
Issue. 4,
p.
433.
Grilitskii, D. V.
and
Shelestovskii, B. G.
1970.
The axisymmetric contact problem of thermoelasticity for a transversely isotropic half-space.
Soviet Applied Mechanics,
Vol. 6,
Issue. 8,
p.
807.
Datta, S. K.
1970.
The diffraction of a plane compressional elastic wave by a rigid circular disc.
Quarterly of Applied Mathematics,
Vol. 28,
Issue. 1,
p.
1.
Dhaliwal, Ranjit S.
1971.
The Steady State Thermoelastic Mixed Boundary Value Problem for the Elastic Layer.
SIAM Journal on Applied Mathematics,
Vol. 20,
Issue. 1,
p.
131.
Khadem, R.
1971.
On two pairs of simultaneous dual integral equations.
Journal of Engineering Mathematics,
Vol. 5,
Issue. 2,
p.
121.
Jain, D. L.
and
Kanwal, R. P.
1972.
Three-part boundary value problems in potential and generalized axially symmetric potential theories.
Journal d'Analyse Mathématique,
Vol. 25,
Issue. 1,
p.
107.
Grilitskii, D. V.
and
Shelestovskii, B. G.
1973.
Pressure of a hot annular stamp in a transversally isotropic half-space with heat transfer at the boundary.
Soviet Applied Mechanics,
Vol. 9,
Issue. 3,
p.
255.
Clements, D. L.
and
Love, E. R.
1974.
Potential problems involving an annulus.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 76,
Issue. 1,
p.
313.
Shibuya, T.
Nakahara, I.
and
Koizumi, T.
1975.
The Axisymmetric Distribution of Stresses in an Infinite Elastic Solid Containing a Flat Annular Crack under Internal Pressure.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 55,
Issue. 7-8,
p.
395.
Love, E. R.
and
Clements, D. L.
1976.
A transformation of Cooke's treatment of some triple integral equations.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 19,
Issue. 3,
p.
259.