Numerical integration by systematic sampling
Published online by Cambridge University Press: 24 October 2008
Extract
Recent investigations by F. Yates (1) in agricultural statistics suggest a mathematical problem which may be formulated as follows. A function f(x) is known to be of bounded variation and Lebesgue integrable on the range −∞ < x < ∞, and its integral over this range is to be determined. In default of any knowledge of the position of the non-negligible values of the function the best that can be done is to calculate the infinite sum
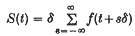
for some suitable δ and an arbitrary origin t, where s ranges over all possible positive and negative integers including zero. S is evidently of period δ in t and ranges over all its values as t varies from 0 to δ. Previous writers (Aitken (2), p. 45, and Kendall (3)) have examined the resulting errors for fixed t. (They considered only symmetrical functions, and supposed one of the lattice points to be located at the centre.) Here we do not restrict ourselves to symmetrical functions and consider the likely departure of S(t) from J (the required integral) when t is a random variable uniformly distributed in (0, δ). It will be shown that S(t) is distributed about J as mean value, with a variance which will be evaluated as a function of δ, the scale of subdivision.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 1 , January 1950 , pp. 111 - 115
- Copyright
- Copyright © Cambridge Philosophical Society 1950
References
REFERENCES
- 27
- Cited by




