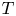1. An alternative and a simple pricing formula
For the sake of completeness, we first summarize the modeling framework considered by Zhu and He [Reference Zhu and He3]. An equivalent martingale measure ![]() $Q$ was constructed with the underlying price following
$Q$ was constructed with the underlying price following
with ![]() $\tau =T-t$.
$\tau =T-t$. ![]() $\ell (y)$ is defined in Section 3.1 of Zhu and He [Reference Zhu and He3], given by
$\ell (y)$ is defined in Section 3.1 of Zhu and He [Reference Zhu and He3], given by
and
Here, ![]() $W_1$ and
$W_1$ and ![]() $W_2$ are two Brownian motions independent of each other, with
$W_2$ are two Brownian motions independent of each other, with ![]() $N(\cdot )$ being a standard normal distribution function. Note that this particular dynamic yields
$N(\cdot )$ being a standard normal distribution function. Note that this particular dynamic yields ![]() $E^Q(e^{-r(T-t)}S(T)\mid \mathcal {F}_t)=S(t)$ [Reference Zhu and He3], and for
$E^Q(e^{-r(T-t)}S(T)\mid \mathcal {F}_t)=S(t)$ [Reference Zhu and He3], and for ![]() $\epsilon =0$, it reduces to the standard Black–Scholes framework.
$\epsilon =0$, it reduces to the standard Black–Scholes framework.
It should be remarked that the formula Zhu and He derived actually involves the integral of the product combining the Gaussian density with its corresponding distribution function, which is relatively complicated for numerical implementation. This has prompted us to try to find a simpler one. In fact, European call option prices have an expression of
where ![]() $\mathcal {F}_t=\sigma \{(W_1(u),W_2(u));0\leq u\leq t\}$.
$\mathcal {F}_t=\sigma \{(W_1(u),W_2(u));0\leq u\leq t\}$.
Let ![]() $W_1(t)=x$ and
$W_1(t)=x$ and ![]() $R(t)=|W_2(t)|=y$. Then,
$R(t)=|W_2(t)|=y$. Then, ![]() $X(t)=\sqrt {1-\epsilon ^2}x+\epsilon y$. Define
$X(t)=\sqrt {1-\epsilon ^2}x+\epsilon y$. Define
so that the call option price has an alternative expression of
where ![]() $f(a_1,a_2)=f_{(|W_2(T)|,W_1(T))\mid (|W_2(t)|,W_1(t))}(a_1,a_2\mid y,x)$ is a conditional probability density function, which is further given by
$f(a_1,a_2)=f_{(|W_2(T)|,W_1(T))\mid (|W_2(t)|,W_1(t))}(a_1,a_2\mid y,x)$ is a conditional probability density function, which is further given by
with
 \begin{align*} f_1(a_1)& =f_{|W_2(T)|\mid|W_2(t)|}(a_1\mid y)=\frac{1}{\sqrt{2\pi\tau}}(e^{-{(a_1-y)^2}/{2\tau}}+e^{-{(a_1+y)^2}/{2\tau}}),\quad 0\leq a_1<\infty,\\ f_2(a_2)& =f_{W_1(T)\mid W_1(t)}(a_2\mid x)=\frac{e^{-{(a_2-x)^2}/{2\tau}}}{\sqrt{2\pi\tau}},\quad -\infty < a_2<\infty. \end{align*}
\begin{align*} f_1(a_1)& =f_{|W_2(T)|\mid|W_2(t)|}(a_1\mid y)=\frac{1}{\sqrt{2\pi\tau}}(e^{-{(a_1-y)^2}/{2\tau}}+e^{-{(a_1+y)^2}/{2\tau}}),\quad 0\leq a_1<\infty,\\ f_2(a_2)& =f_{W_1(T)\mid W_1(t)}(a_2\mid x)=\frac{e^{-{(a_2-x)^2}/{2\tau}}}{\sqrt{2\pi\tau}},\quad -\infty < a_2<\infty. \end{align*}
The derivation of our simpler formula requires some fundamental results that need to be derived first, which are provided below.
Proposition 1.1. If ![]() $I(m,\sigma )$ denotes
$I(m,\sigma )$ denotes
where ![]() $a,a_1,a_2,m,\sigma \in \mathbb {R}$, then we have its simplified value shown in the following formula
$a,a_1,a_2,m,\sigma \in \mathbb {R}$, then we have its simplified value shown in the following formula
where
 \begin{align*} h_1& =\frac{a_1+a_2(m+a\sigma^2)}{\sqrt{1+a_2^2\sigma^2}},\quad h_2=\frac{-m-a\sigma^2}{\sigma},\quad \tilde{a}_1=\frac{h_2-rh_1}{h_1\sqrt{1-r^2}},\\ \tilde{a}_2& =\frac{h_1-rh_2}{h_2\sqrt{1-r^2}},\quad r=\frac{-a_2\sigma}{\sqrt{1+a_2^2\sigma^2}}, \end{align*}
\begin{align*} h_1& =\frac{a_1+a_2(m+a\sigma^2)}{\sqrt{1+a_2^2\sigma^2}},\quad h_2=\frac{-m-a\sigma^2}{\sigma},\quad \tilde{a}_1=\frac{h_2-rh_1}{h_1\sqrt{1-r^2}},\\ \tilde{a}_2& =\frac{h_1-rh_2}{h_2\sqrt{1-r^2}},\quad r=\frac{-a_2\sigma}{\sqrt{1+a_2^2\sigma^2}}, \end{align*}
with the Owen's ![]() $T$ function denoted by
$T$ function denoted by ![]() $T(h,a)$. The relationship connecting the Owen's
$T(h,a)$. The relationship connecting the Owen's ![]() $T$ function with the bivariate normal probability is provided in the Appendix.
$T$ function with the bivariate normal probability is provided in the Appendix.
Proof. We can re-write
 \begin{align} I(m,\sigma)& =\frac{e^{\frac{1}{2}(a^2\sigma^2+2am)}}{\sigma\sqrt{2\pi}}\int_0^{\infty}N(a_1+a_2x) e^{-{(x-(m+a\sigma^2))^2}/{2\sigma^2}}\,dx\nonumber\\ & =\frac{e^{\frac{1}{2}(a^2\sigma^2+2am)}}{\sigma\sqrt{2\pi}}\int_0^{\infty} \int_{-\infty}^{a_1+a_2x}N(u)e^{-{(x-(m+a\sigma^2))^2}/{2\sigma^2}}\,du\,dx, \end{align}
\begin{align} I(m,\sigma)& =\frac{e^{\frac{1}{2}(a^2\sigma^2+2am)}}{\sigma\sqrt{2\pi}}\int_0^{\infty}N(a_1+a_2x) e^{-{(x-(m+a\sigma^2))^2}/{2\sigma^2}}\,dx\nonumber\\ & =\frac{e^{\frac{1}{2}(a^2\sigma^2+2am)}}{\sigma\sqrt{2\pi}}\int_0^{\infty} \int_{-\infty}^{a_1+a_2x}N(u)e^{-{(x-(m+a\sigma^2))^2}/{2\sigma^2}}\,du\,dx, \end{align}
which implies
Here, the joint distribution of ![]() $X$ and
$X$ and ![]() $Y$ gives a bivariate Gaussian one, the covariance matrix of which is
$Y$ gives a bivariate Gaussian one, the covariance matrix of which is ![]() $\left (\begin {smallmatrix} \sigma ^2 & 0\\ 0 & 1 \end {smallmatrix}\right )$ along with its mean as
$\left (\begin {smallmatrix} \sigma ^2 & 0\\ 0 & 1 \end {smallmatrix}\right )$ along with its mean as ![]() $(m+a\sigma ^2,0)$. By further denoting
$(m+a\sigma ^2,0)$. By further denoting ![]() $Z=Y-a_1-a_2X$, one would be able to obtain
$Z=Y-a_1-a_2X$, one would be able to obtain ![]() $E(Z)=-a_1-a_2(m+a\sigma ^2)$, variance
$E(Z)=-a_1-a_2(m+a\sigma ^2)$, variance ![]() ${\rm Var}(Z)=1+a_2^2\sigma ^2$ and covariance with
${\rm Var}(Z)=1+a_2^2\sigma ^2$ and covariance with ![]() $X$ being
$X$ being ![]() ${\rm Cov}(Z,X)=-a_2\sigma ^2$. As a result, the unknown probability involved in Eq. (7) can then be simplified through
${\rm Cov}(Z,X)=-a_2\sigma ^2$. As a result, the unknown probability involved in Eq. (7) can then be simplified through
 \begin{align*} I(m,\sigma)& =e^{\frac{1}{2}(a^2\sigma^2+2am)}P(Z\leq 0, X> 0)\\ & =e^{\frac{1}{2}(a^2\sigma^2+2am)}(P(X>0)-P(Z> 0, X> 0))\\ & =e^{\frac{1}{2}(a^2\sigma^2+2am)}\left(P(X>0)-P\left(Z_1> \frac{a_1+a_2(m+a\sigma^2)}{\sqrt{1+a_2^2\sigma^2}}, Z_2>\frac{-m-a\sigma^2}{\sigma}\right) \right), \end{align*}
\begin{align*} I(m,\sigma)& =e^{\frac{1}{2}(a^2\sigma^2+2am)}P(Z\leq 0, X> 0)\\ & =e^{\frac{1}{2}(a^2\sigma^2+2am)}(P(X>0)-P(Z> 0, X> 0))\\ & =e^{\frac{1}{2}(a^2\sigma^2+2am)}\left(P(X>0)-P\left(Z_1> \frac{a_1+a_2(m+a\sigma^2)}{\sqrt{1+a_2^2\sigma^2}}, Z_2>\frac{-m-a\sigma^2}{\sigma}\right) \right), \end{align*}
where both ![]() $Z_1$ and
$Z_1$ and ![]() $Z_2$ follow a standard normal distribution and their correlation is captured with a parameter
$Z_2$ follow a standard normal distribution and their correlation is captured with a parameter ![]() $r$. Thus, considering how the Owen's
$r$. Thus, considering how the Owen's ![]() $T$ function is related to the bivariate normal CDF, one can obtain
$T$ function is related to the bivariate normal CDF, one can obtain
 \begin{align} I(m,\sigma)& =e^{\frac{1}{2}(a^2\sigma^2+2am)}\left(N\left(\frac{m+a\sigma^2}{\sigma}\right) -P(Z_1>h_1,Z_2>h_2)\right) \nonumber\\ & =e^{\frac{1}{2}(a^2\sigma^2+2am)}\left(N({-}h_2)-\left(1-\frac{N(h_1)+N(h_2)}{2}-T(h_1,\tilde{a}_1)-T(h_2,\tilde{a}_2)\right)\right) \nonumber\\ & =e^{\frac{1}{2}(a^2\sigma^2+2am)}\left(\frac{N(h_1)-N(h_2)}{2}-T(h_1,\tilde{a}_1)-T(h_2,\tilde{a}_2)\right). \end{align}
\begin{align} I(m,\sigma)& =e^{\frac{1}{2}(a^2\sigma^2+2am)}\left(N\left(\frac{m+a\sigma^2}{\sigma}\right) -P(Z_1>h_1,Z_2>h_2)\right) \nonumber\\ & =e^{\frac{1}{2}(a^2\sigma^2+2am)}\left(N({-}h_2)-\left(1-\frac{N(h_1)+N(h_2)}{2}-T(h_1,\tilde{a}_1)-T(h_2,\tilde{a}_2)\right)\right) \nonumber\\ & =e^{\frac{1}{2}(a^2\sigma^2+2am)}\left(\frac{N(h_1)-N(h_2)}{2}-T(h_1,\tilde{a}_1)-T(h_2,\tilde{a}_2)\right). \end{align}
This completes the proof.
From Equation (4), we obtain
where
Using the standard Black–Scholes formula yields
where
 \begin{align*} d_1& ={-}\frac{\ln(K)-(\ln(M)+\sigma\epsilon u+\sigma\sqrt{1-\epsilon^2}x+\sigma^2(1-\epsilon^2)\tau))}{\sigma\sqrt{1-\epsilon^2}\sqrt{\tau}}\\ d_2& =d_1-\sigma\sqrt{1-\epsilon^2}\sqrt{\tau}. \end{align*}
\begin{align*} d_1& ={-}\frac{\ln(K)-(\ln(M)+\sigma\epsilon u+\sigma\sqrt{1-\epsilon^2}x+\sigma^2(1-\epsilon^2)\tau))}{\sigma\sqrt{1-\epsilon^2}\sqrt{\tau}}\\ d_2& =d_1-\sigma\sqrt{1-\epsilon^2}\sqrt{\tau}. \end{align*}
Therefore, Eq. (9) further leads to
where
 \begin{align*} c_1& ={-}\frac{\ln(K)-(\ln(M)+\sigma\sqrt{1-\epsilon^2}x+\sigma^2(1-\epsilon^2)\tau))}{\sigma\sqrt{1-\epsilon^2}\sqrt{\tau}},\\ c_2& ={+}\frac{\epsilon}{\sqrt{1-\epsilon^2}\sqrt{\tau}},\\ c_3& =c_1-\sigma\sqrt{1-\epsilon^2}\sqrt{\tau}. \end{align*}
\begin{align*} c_1& ={-}\frac{\ln(K)-(\ln(M)+\sigma\sqrt{1-\epsilon^2}x+\sigma^2(1-\epsilon^2)\tau))}{\sigma\sqrt{1-\epsilon^2}\sqrt{\tau}},\\ c_2& ={+}\frac{\epsilon}{\sqrt{1-\epsilon^2}\sqrt{\tau}},\\ c_3& =c_1-\sigma\sqrt{1-\epsilon^2}\sqrt{\tau}. \end{align*}
Using Proposition 1.1 leads to
with
 \begin{align*} J_1& =\int_{0}^{\infty}e^{\sigma\epsilon u}N(c_1+c_2u)f_1(u)\,du=I_1(y,\lambda,c_1,c_2)+I_1({-}y,\lambda,c_1,c_2)\\ J_2& =\int_{0}^{\infty}N(c_3+c_2u)f_1(u)\,du=I_1(y,0,c_1,c_2)+I_1({-}y,0,c_1,c_2), \end{align*}
\begin{align*} J_1& =\int_{0}^{\infty}e^{\sigma\epsilon u}N(c_1+c_2u)f_1(u)\,du=I_1(y,\lambda,c_1,c_2)+I_1({-}y,\lambda,c_1,c_2)\\ J_2& =\int_{0}^{\infty}N(c_3+c_2u)f_1(u)\,du=I_1(y,0,c_1,c_2)+I_1({-}y,0,c_1,c_2), \end{align*}
where ![]() $\lambda =\epsilon \sigma$ is introduced for notation ease. If we apply Proposition 1.1 once again, we obtain
$\lambda =\epsilon \sigma$ is introduced for notation ease. If we apply Proposition 1.1 once again, we obtain
 \begin{align*} I_1(y,\lambda,c_1,c_2)& =\int_{0}^{\infty}e^{\lambda u}N(c_1+c_2u)\frac{e^{-{(u-y)^2}/{2\tau}}}{\sqrt{2\pi\tau}}\,du\\ & =e^{\frac{1}{2}(\lambda^2\tau+2\lambda y)}\left(\frac{N(H_1)-N(H_2)}{2}-T(H_1,A_1)-T(H_2,A_2)\right), \end{align*}
\begin{align*} I_1(y,\lambda,c_1,c_2)& =\int_{0}^{\infty}e^{\lambda u}N(c_1+c_2u)\frac{e^{-{(u-y)^2}/{2\tau}}}{\sqrt{2\pi\tau}}\,du\\ & =e^{\frac{1}{2}(\lambda^2\tau+2\lambda y)}\left(\frac{N(H_1)-N(H_2)}{2}-T(H_1,A_1)-T(H_2,A_2)\right), \end{align*}
where
 \begin{align*} H_1& =\frac{c_1+c_2(y+\lambda\tau)}{\sqrt{1+c_2^2\tau}},~H_2=\frac{-y-\lambda\tau}{\sqrt{\tau}},~ A_1=\frac{H_2-R_1H_1}{H_1\sqrt{1-R_1^2}},\\ A_2& =\frac{H_1-R_1H_2}{H_2\sqrt{1-R_1^2}},~R_1=\frac{-c_2\sqrt{\tau}}{\sqrt{1+c_2^2\tau}}. \end{align*}
\begin{align*} H_1& =\frac{c_1+c_2(y+\lambda\tau)}{\sqrt{1+c_2^2\tau}},~H_2=\frac{-y-\lambda\tau}{\sqrt{\tau}},~ A_1=\frac{H_2-R_1H_1}{H_1\sqrt{1-R_1^2}},\\ A_2& =\frac{H_1-R_1H_2}{H_2\sqrt{1-R_1^2}},~R_1=\frac{-c_2\sqrt{\tau}}{\sqrt{1+c_2^2\tau}}. \end{align*}
This clearly shows that the pricing formula presented in Eq. (13) is fully analytical now.
2. Accuracy tests
This section is devoted to checking the correctness of the simple option pricing formula derived in the above section using the Monte Carlo benchmark. The certain parameter values we select are ![]() $r=0.1$,
$r=0.1$, ![]() $S(t)=110$,
$S(t)=110$, ![]() $\sigma =\sqrt {0.4}$. It should be pointed out that at current time
$\sigma =\sqrt {0.4}$. It should be pointed out that at current time ![]() $t$, we observe the current stock price
$t$, we observe the current stock price ![]() $S(t)$ in the market, but are unable to observe the current (starting) values of the Brownian motions,
$S(t)$ in the market, but are unable to observe the current (starting) values of the Brownian motions, ![]() $W_i(t),\ i=1,2$. Therefore, in practical applications,
$W_i(t),\ i=1,2$. Therefore, in practical applications, ![]() $W_i(t),\ i=1,2$ are actually treated as model parameters and can be calibrated together with other model parameters (e.g.,
$W_i(t),\ i=1,2$ are actually treated as model parameters and can be calibrated together with other model parameters (e.g., ![]() $\sigma$ and
$\sigma$ and ![]() $\delta$) with real data. For illustration purposes, we fix
$\delta$) with real data. For illustration purposes, we fix ![]() $W_i(t),\ i=1,2$ as 0.02 and
$W_i(t),\ i=1,2$ as 0.02 and ![]() $-$0.01, respectively. We also select 0.25 as the value of the time to maturity, and the skewness parameter
$-$0.01, respectively. We also select 0.25 as the value of the time to maturity, and the skewness parameter ![]() $\epsilon$ is assumed to be equal to 0.5.
$\epsilon$ is assumed to be equal to 0.5.
To be sure that we did not make any mistakes when deriving the pricing formula, we need to address its correctness. We accomplish this task by benchmarking our results using the Monte Carlo simulation, with the parameters kept as the same. Figure 1(a) displays the comparison results, which obviously show the point-wise agreement of both prices, and the relative error displayed in Figure 1(b) remains below 0.24%. These are actually a verification of the formula.

Figure 1. A demonstration of the accuracy. (a) The two prices. (b) Relative difference.
3. Conclusion
In this article, we price European options with the geometric skew Brownian motion considered in Zhu and He [Reference Zhu and He3]. A simpler pricing formula is presented using the standard normal distribution function and Owen's ![]() $T$ function. The accuracy of the formula is also numerically verified.
$T$ function. The accuracy of the formula is also numerically verified.
Funding
This work is supported by the National Natural Science Foundation of China (No. 12101554; No. 72002201), the Fundamental Research Funds for Zhejiang Provincial Universities (No. GB202103001), and the Advanced Research Funds of Zhejiang University of Technology (No. SKY-ZX-20220212).
Competing interest
The authors declare that they have no conflict of interest.
Appendix
Relationship between the Owen's  $T$ function and bivariate normal density [Reference Owen1,Reference Sowden and Ashford2]
$T$ function and bivariate normal density [Reference Owen1,Reference Sowden and Ashford2]
Let a pair of bivariate standard normal variables ![]() $(X_1,X_2)$ be correlated with each other with a parameter
$(X_1,X_2)$ be correlated with each other with a parameter ![]() $r$. We have the following relation
$r$. We have the following relation
where
and ![]() $T(u,b)$ is Owen's
$T(u,b)$ is Owen's ![]() $T$ function formulated as
$T$ function formulated as
Furthermore, it can be shown that
 \begin{align*} F({-}u_1, u_2, r) & ={-}F(u_1, u_2, -r) +N({-}u_2),\\ F(u_1,- u_2,r) & ={-}F(u_1,u_2, -r)+ N({-}u_1),\\ F({-}u_1,- u_2, r) & = F(u_1, u_2, r) + 1-N({-}u_1)-N({-}u_2). \end{align*}
\begin{align*} F({-}u_1, u_2, r) & ={-}F(u_1, u_2, -r) +N({-}u_2),\\ F(u_1,- u_2,r) & ={-}F(u_1,u_2, -r)+ N({-}u_1),\\ F({-}u_1,- u_2, r) & = F(u_1, u_2, r) + 1-N({-}u_1)-N({-}u_2). \end{align*}
As a result, is suffices to only cope with ![]() $u_1$ and
$u_1$ and ![]() $u_2$ when they are not negative.
$u_2$ when they are not negative.