Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-26T23:55:50.690Z Has data issue: false hasContentIssue false
  • English
  • Français

Linearization of holomorphic germs with quasi-parabolic fixed points

Published online by Cambridge University Press:  01 June 2008

FENG RONG
FENG RONG*
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA (email: frong@umich.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let f be a germ of a holomorphic diffeomorphism of 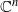with the origin O being a quasi-parabolic fixed point, i.e. the spectrum of dfO consists of 1 and e2iπθj with 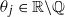. We show that f is locally holomorphically conjugated to its linear part, if f is of some particular form and its eigenvalues satisfy certain arithmetic conditions. When the spectrum of dfO does not consist of any 1’s, this is the classical result of Siegel [C. L. Siegel. Iteration of analytic functions. Ann. of Math.43 (1942), 607–612] and Brjuno [A. D. Brjuno. Analytic form of differential equations. Trans. Moscow Math. Soc.25 (1971), 131–288; 26 (1972), 199–239].

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 3 , June 2008 , pp. 979 - 986
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Abate, M.. Discrete local holomorphic dynamics. Proc. 13th Seminar on Analysis and its Applications (Isfahan, March 2003).Google Scholar
[2]Bracci, F.. Local dynamics of holomorphic diffeomorphisms. Boll. UMI (9) 7-B (2004), 609–636.Google Scholar
[3]Bracci, F. and Molino, L.. The dynamics near quasi-parabolic fixed points of holomorphic diffeomorphisms in . Amer. J. Math. 126 (2004), 671–686.CrossRefGoogle Scholar
[4]Brjuno, A. D.. Analytic form of differential equations. Trans. Moscow Math. Soc. 25 (1971), 131–288; 26 (1972), 199–239.Google Scholar
[5]Cremer, H.. Zum zentrumproblem. Math. Ann. 98 (1927), 151–163.Google Scholar
[6]Cremer, H.. Über die häufigkeit der nichtzentren. Math. Ann. 115 (1938), 573–580.CrossRefGoogle Scholar
[7]Hakim, M.. Analytic transformations of tangent to the identity. Duke Math. J. 92(2) (1998), 403–428.Google Scholar
[8]Hakim, M.. Transformations tangent to the identity. Stable pieces of manifolds. Preprint, 1998.Google Scholar
[9]Nishimura, Y.. Automorphismes analytiques admettant des sous-variétés de points fixés attractives dans la direction transversale. J. Math. Kyoto Univ. 23(2) (1983), 289–299.Google Scholar
[10]Pöschel, J.. On invariant manifolds of complex analytic mappings near fixed points. Exp. Math. 4 (1986), 97–109.Google Scholar
[11]Rong, F.. Critically Finite Maps, Attractors and Local Dynamics. University of Michigan, Ann Arbor, 2007.Google Scholar
[12]Rong, F.. Quasi-parabolic analytic transformations of . J. Math. Anal. Appl. to appear.Google Scholar
[13]Siegel, C. L.. Iteration of analytic functions. Ann. of Math. 43 (1942), 607–612.CrossRefGoogle Scholar
[14]Siegel, C. L.. Über die Normalform analytischer Differentialgleichungen in der Näheeiner Gleichgewichtslösung. Nachr. Akad. Wiss. Göttingen, Phys. Kl. (1952), 21–30.Google Scholar
[15]Siegel, C. L. and Moser, J.. Lectures on Celestial Mechanics. Springer, Berlin, 1971.Google Scholar