Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T08:36:47.672Z Has data issue: false hasContentIssue false
  • English
  • Français

A natural pseudometric on homotopy groups of metric spaces

Part of: Homotopy theory Spaces with richer structures Maps and general types of spaces defined by maps Homotopy groups

Published online by Cambridge University Press:  08 November 2023

Jeremy Brazas Open the ORCID record for Jeremy Brazas [Opens in a new window]  and
Paul Fabel
Jeremy Brazas*
Affiliation:
West Chester University, 25 University Avenue, West Chester, PA 19383, United States of America
Paul Fabel
Affiliation:
Mississippi State University, 410 Allen Hall, 175 President’s Circle, Mississippi State, MS, 39762, United States of America
*
Corresponding author: Jeremy Brazas; Email: jbrazas@wcupa.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

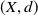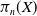For a path-connected metric space $(X,d)$, the $n$-th homotopy group $\pi _n(X)$ inherits a natural pseudometric from the $n$-th iterated loop space with the uniform metric. This pseudometric gives 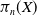$\pi _n(X)$ the structure of a topological group, and when 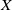$X$ is compact, the induced pseudometric topology is independent of the metric 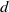$d$. In this paper, we study the properties of this pseudometric and how it relates to previously studied structures on 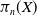$\pi _n(X)$. Our main result is that the pseudometric topology agrees with the shape topology on 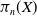$\pi _n(X)$ if 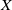$X$ is compact and 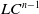$LC^{n-1}$ or if 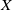$X$ is an inverse limit of finite polyhedra with retraction bonding maps.

Keywords

topological homotopy grouppseudometric groupshape homotopy groupshape topology

MSC classification

Primary: 55Q52: Homotopy groups of special spaces 54E35: Metric spaces, metrizability 55Q07: Shape groups
Secondary: 55Q05: Homotopy groups, general; sets of homotopy classes 54C56: Shape theory 55P55: Shape theory
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 66 , Issue 1 , January 2024 , pp. 162 - 174
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdullahi Rashid, M., Jamali, N., Mashayekhy, B., Pashaei, S. Z. and Torabi, H., On subgroup topologies on the fundamental group, Hacettepe J. Math. Stat. 49(3) (2020), 935–949.CrossRefGoogle Scholar
Abdullahi Rashid, M., Pashaei, S. Z., Mashayekhy, B. and Torabi, H., On the Whisker Topology on Fundamental Group, in Conference Paper from 46th Annual Iranian Mathematics Conference 46 (2015).Google Scholar
Aceti, J. and Brazas, J., Elements of homotopy groups undetectable by polyhedral approximation, Pacific J. Math. 322(2) (2023), 221–242.CrossRefGoogle Scholar
Akbar Bahredar, A., Kouhestani, N. and Passandideh, H., The $n$ -dimensional Spanier group , Filomat 35(9) (2021), 3169–3182.CrossRefGoogle Scholar
Arhangel’skii, A. and Tkachenko, M., Topological groups and related structures, in Pure and applied mathematics, Atlantis studies in mathematics, 2008).Google Scholar
Barratt, M. G. and Milnor, J., An example of anomalous singular homology, Proc. Am. Math. Soc. 13(2) (1962), 293–297.CrossRefGoogle Scholar
Borsuk, K., On the $n$ -movability , Bull. Acad. Polon. Sci. Ser. Sci. Math. Astr. Phys. 20 (1972), 859–864.Google Scholar
Brazas, J., The topological fundamental group and free topological groups, Topol. Appl. 158 (2011), 779–802.CrossRefGoogle Scholar
Brazas, J., The fundamental group as a topological group, Topol. Appl. 160 (2013), 170–188.CrossRefGoogle Scholar
Brazas, J., On the discontinuity of the $\pi _1$ -action , Topol. Appl. 247 (2018), 29–40.CrossRefGoogle Scholar
Brazas, J. and Fabel, P., On fundamental groups with the quotient topology, J. Homot. Relat. Struct. 10 (2015), 71–91.CrossRefGoogle Scholar
Brazas, J. and Fabel, P., Thick Spanier groups and the first shape group, Rocky Mount. J. Math. 44 (2014), 1415–1444.CrossRefGoogle Scholar
Bridson, M. R. and Haefliger, A., Metric spaces of non-positive curvature, Grundlehren der mathematischen Wissenschaften, vol. 319 (Springer, 1999).CrossRefGoogle Scholar
Calcut, J. S. and McCarthy, J. D., Discreteness and homogeneity of the topological fundamental group, Topol. Proc. 34 (2009), 339–349.Google Scholar
Conner, G., Meilstrup, M., Repovs, D., Zastrow, A. and Zeljko, M., On small homotopies of loops, Topol. Appl. 155 (2008), 1089–1097.CrossRefGoogle Scholar
Dugundji, J., A topologized fundamental group, Proc. Natl. Acad. Sci. 36 (1950), 141–143.CrossRefGoogle Scholar
Eda, K. and Kawamura, K., Homotopy and homology groups of the $n$ -dimensional Hawaiian earring , Fund. Math. 165 (2000), 17–28.CrossRefGoogle Scholar
Engelking, R., General topology (Heldermann Verlag, Berlin, 1989).Google Scholar
Fabel, P., Multiplication is discontinuous in the Hawaiian earring group, Bull. Pol. Acad. Sci. Math. 59 (2011), 77–83.CrossRefGoogle Scholar
Fabel, P., Compactly generated quasitopological homotopy groups with discontinuous multiplication, Topol. Proc. 40 (2012), 303–309.Google Scholar
Mardešić, S. and Segal, J., Shape theory (North-Holland Publishing Company, 1982).Google Scholar
Spanier, E., Algebraic topology (McGraw-Hill, 1966).Google Scholar
Virk, Z. and Zastrow, A., A new topology on the universal path space, Topol. Appl. 231(1) (2017), 186–196.CrossRefGoogle Scholar
Wada, H., Local connectivity of mapping spaces, Duke Math. J. 22 (1955), 419–425.CrossRefGoogle Scholar