Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-09T11:30:49.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Indefinite quadratic polynomials

Published online by Cambridge University Press:  18 May 2009

R. J. Cook
R. J. Cook
Affiliation:
University of Sheffield, Sheffield S10 2Tn
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let

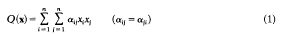
be an indefinite quadratic form with real coefficients. A well-known result, due to Birch, Davenport and Ridout [1], [5] and [6], states that if n ≥21 then for any ε > 0 there is an integer vector x ≠O such that

Recently [3] we have quantified this result, obtaining a function g(n) such that g(n)→ ½ as n n→ ∞ and such that for any η > 0 and all large enough X there is an integer vector x satisfying

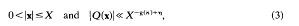
where |x| = max |xi|and the implicit constant in Vinogradov's ≪-notation is independent of X.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 24 , Issue 2 , July 1983 , pp. 133 - 138
Copyright
Copyright © Glasgow Mathematical Journal Trust 1983

References

REFERENCES

1.Birch, B. J. and Davenport, H., Indefinite quadratic forms in many variables, Mathematika 5 (1958), 8–12.CrossRefGoogle Scholar
2.Birch, B. J. and Davenport, H., On a theorem of Davenport and Heilbronn, Acta Math. 100 (1958), 259–279.CrossRefGoogle Scholar
3.Cook, R. J., Small values of indefinite quadratic forms and polynomials in many variables (submitted for publication).Google Scholar
4.Davenport, H., Indefinite quadratic forms in many variables, Mathematika 3 (1956), 81–101.CrossRefGoogle Scholar
5.Davenport, H. and Ridout, D., Indefinite quadratic forms, Proc. London Math. Soc. (3) 9 (1959), 554–555.Google Scholar
6.Ridout, D., Indefinite quadratic forms, Mathematika 5 (1958), 122–124.CrossRefGoogle Scholar