Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-07T17:17:20.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Weight functions on extensions of the compound manual

Published online by Cambridge University Press:  18 May 2009

Patricia J. Frazer ,
David J. Foulis  and
Charles H. Randall
Patricia J. Frazer
Affiliation:
University of Massachusetts, Amherst Massachusetts 01002
David J. Foulis
Affiliation:
University of Massachusetts, Amherst Massachusetts 01002
Charles H. Randall
Affiliation:
University of Massachusetts, Amherst Massachusetts 01002
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It has been shown ([8], [2], [1], [3], [9]) that a collection of physical operations or experiments can be represented by a nonempty set of nonempty sets satisfying certain technical conditions. Such a set 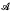is called a manual. The operations in 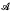are looked at as having no “before” and no “after”, i.e., they are isolated in time. If we wish to look at connected sequences of operations—in particular, if we wish to condition by events in 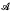—we must look at the compound manual 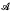c whose elements represent compound operations built up from the operations in the base manual .

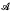Type
Research Article
Information
Glasgow Mathematical Journal , Volume 21 , Issue 2 , July 1980 , pp. 97 - 101
Copyright
Copyright © Glasgow Mathematical Journal Trust 1980

References

REFERENCES

1.Foulis, D. J. and Randall, C. H., Operational statistics I, Basic Concepts, J. Mathematical. Phys. 13 (1972), 1667–1675.CrossRefGoogle Scholar
2.Foulis, D. J. and Randall, C. H., Empirical logic and quantum mechanics, Synthese 29 (1974), 81–111.Google Scholar
3.Foulis, D. J. and Randall, C. H.. The empirical logic approach to the physical sciences, in Foundations of quantum mechanics and ordered linear spaces, (Springer-Verlag, 1974).Google Scholar
4.Foulis, D. J. and Randall, C. H.. The stability of pure weights under conditioning, Glasgow Math. J. 15 (1974), 5–12.Google Scholar
5.Gaudard, M. A. and Weaver, R. J., Finitary embeddings of certain generalized sample spaces, Trans. Amer. Math. Soc. 207 (1975), 293–307.CrossRefGoogle Scholar
6.Horn, A. and Tarski, A., Measures in Boolean Algebras, Trans. Amer. Math. Soc. 64 (1948), 467–497.CrossRefGoogle Scholar
7.Mackey, G. W.. The mathematical foundations of quantum mechanics, (Benjamin, 1963).Google Scholar
8.Randall, C. H. and Foulis, D. J., The operational approach to quantum mechanics, in Hooker, C. A. (Ed.), The logico-algebraic approach to quantum mechanics III, (D. Reidel Publishing Co., 1977).Google Scholar
9.Randall, C. H. and Foulis, D. J.. A mathematical setting for inductive reasoning, in Hooker, C. A. (Ed.), Foundations of probability theory, statistical inference, and statistical theories of science III, (D. Reidel Publishing Co., 1976), 169–205.CrossRefGoogle Scholar