Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-27T19:58:36.731Z Has data issue: false hasContentIssue false
  • English
  • Français

Burstein’s permutation conjecture, Hong and Li’s inversion sequence conjecture and restricted Eulerian distributions

Part of: Combinatorics

Published online by Cambridge University Press:  23 October 2023

Shane Chern Open the ORCID record for Shane Chern [Opens in a new window] ,
Shishuo Fu Open the ORCID record for Shishuo Fu [Opens in a new window]  and
Zhicong Lin
Shane Chern
Affiliation:
Department of Mathematics and Statistics, Dalhousie University, Halifax, NS, Canada (chenxiaohang92@gmail.com; xh375529@dal.ca)
Shishuo Fu
Affiliation:
College of Mathematics and Statistics, Chongqing University, Huxi Campus, Chongqing, P.R. China (fsshuo@cqu.edu.cn)
Zhicong Lin
Affiliation:
Research Center for Mathematics and Interdisciplinary Sciences, Shandong University, Qingdao, Shandong, P.R. China (linz@sdu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

Recently, Hong and Li launched a systematic study of length-four pattern avoidance in inversion sequences, and in particular, they conjectured that the number of 0021-avoiding inversion sequences can be enumerated by the OEIS entry A218225. Meanwhile, Burstein suggested that the same sequence might also count three sets of pattern-restricted permutations. The objective of this paper is not only a confirmation of Hong and Li’s conjecture and Burstein’s first conjecture but also two more delicate generating function identities with the $\mathsf{ides}$ statistic concerned in the restricted permutation case and the 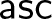$\mathsf{asc}$ statistic concerned in the restricted inversion sequence case, which yield a new equidistribution result.

Keywords

permutationsinversion sequencespattern avoidanceEulerian statisticsgenerating functionsequidistributions

MSC classification

Primary: 05A05: Permutations, words, matrices 05A15: Exact enumeration problems, generating functions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 4 , November 2023 , pp. 1179 - 1201
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Billey, S. C., Jockusch, W. and Stanley, R. P., Some combinatorial properties of Schubert polynomials, J. Algebraic Combin. 2 (4) (1993), 345–374.CrossRefGoogle Scholar
Bloom, J. and Burstein, A., Egge triples and unbalanced Wilf-equivalence, Australas. J. Combin. 64 (1) (2016), 232–251.Google Scholar
Burstein, A. and Pantone, J., Two examples of unbalanced Wilf-equivalence, J. Combin. 6(1–2) (2015), 55–67.Google Scholar
Chern, S., On 0012-avoiding inversion sequences and a conjecture of Lin and Ma, Quaest. Math. 46(4) (2023), 681–694.CrossRefGoogle Scholar
Corteel, S., Martinez, M. A., Savage, C. D. and Weselcouch, M., Patterns in inversion sequences I, Discrete Math. Theor. Comput. Sci. 18(2) (2016), .Google Scholar
Defant, C., Enumeration of stack-sorting preimages via a decomposition lemma, Discrete Math. Theor. Comput. Sci. 22(2) (2021), .Google Scholar
Dumont, D., Interprétations combinatoires des nombres de Genocchi, Duke Math. J. 41 (2) (1974), 305–318.CrossRefGoogle Scholar
Foata, D. and Schützenberger, M.-P., ThéOrie GéoméTrique des Polynômes EuléRiens (Springer-Verlag, Berlin–New York, 1970).CrossRefGoogle Scholar
Fu, S., Lin, Z. and Zeng, J., On two unimodal descent polynomials, Discrete Math. 341(9) (2018), 2616–2626.CrossRefGoogle Scholar
Hong, L. and Li, R., Length-four pattern avoidance in inversion sequences, Electron. J. Combin. 29 (4) (2022), .CrossRefGoogle Scholar
Kitaev, S., Patterns in permutations and words (Springer, Heidelberg, 2011).CrossRefGoogle Scholar
Knuth, D. E., The art of computer programming. Fundamental Algorithms, 3rd edn., Volume 1 (Boston, MA: Addison-Wesley, 1997).Google Scholar
Lin, Z. and Fu, S., On $\underline120$-avoiding inversion and ascent sequences, European J. Combin. 93 (1) (2021), .CrossRefGoogle Scholar
Lin, Z. and Kim, D., A sextuple equidistribution arising in pattern avoidance, J. Combin. Theory Ser. A 155 (1) (2018), 267–286.CrossRefGoogle Scholar
Lin, Z. and Kim, D., Refined restricted inversion sequences, Ann. Comb. 25(4) (2021), 849–875.CrossRefGoogle Scholar
Lin, Z., Patterns of relation triples in inversion and ascent sequences, Theoret. Comput. Sci. 804 (1) (2020), 115–125.CrossRefGoogle Scholar
MacMahon, P. A., Combinatory Analysis (Cambridge University Press, London, 1915/16).Google Scholar
Mansour, T. and Shattuck, M., Pattern avoidance in inversion sequences, Pure Math. Appl. (PU.M.A.) 25(2) (2015), 157–176.Google Scholar
Petersen, T. K., Eulerian Numbers (Birkhäuser/Springer, New York, 2015).CrossRefGoogle Scholar
Savage, C. D. and Schuster, M. J., Ehrhart series of lecture hall polytopes and Eulerian polynomials for inversion sequences, J. Combin. Theory Ser. A 119(4) (2012), 850–870.CrossRefGoogle Scholar
Sloane, N. J. A., On-line encyclopedia of integer sequences. http://oeis.org.Google Scholar
Vatter, V., Permutation classes. Handbook of Enumerative combinatorics, (CRC Press, Boca Raton, FL, 2015).Google Scholar