Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-28T04:37:51.017Z Has data issue: false hasContentIssue false
  • English
  • Français

Some infinite Fibonacci groups

Published online by Cambridge University Press:  20 January 2009

D. L. Johnson
D. L. Johnson
Affiliation:
University of Nottingham
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Fibonacci groups are a special case of the following class of groups first studied by G. A. Miller (7). Given a natural number n, let θ be the automorphism of the free group F = 〈x1, …, xn |〉 of rank n which permutes the subscripts of the generators in accordance with the cycle (1, 2, …, n). Given a word w in F, let R be the smallest normal subgroup of F which contains w and is closed under θ. Then define Gn(w) = F/R and write An(w) for the derived factor group of Gn(w). Putting, for r ≦ 2, k ≦ 1,

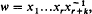
with subscripts reduced modulo n, we obtain the groups F(r, n, k) studied in (1) and (2), while the F(r, n, 1) are the ordinary Fibonacci groups F(r, n) of (3), (5) and (6). To conform with earlier notation, we write A(r, n, k) and A(r, n) for the derived factor groups of F(r, n, k), and F(r, n) respectively.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 19 , Issue 3 , March 1975 , pp. 311 - 314
Copyright
Copyright © Edinburgh Mathematical Society 1975

References

REFERENCES

(1) Campbell, C. M. and Robertson, E. F., A note on a class of generalized Fibonacci groups (to appear).Google Scholar
(2) Campbell, C M. and Robertson, E. F., The orders of certain metacyclic groups, Bull. London Math. Soc. (to appear).Google Scholar
(3) Conway, J. H., Solution to Advanced Problem 5327 Amer. Math. Monthly. 74 (1967), 91–93.CrossRefGoogle Scholar
(4) Dunwoody, M. J., Cyclic presentations and 3-manifolds (to appear).Google Scholar
(5) Johnson, D. L., A note on the Fibonacci groups, Israel J. Math. (to appear).Google Scholar
(6) Johnson, D. L., Wamsley, J. W. and Wright, D., The Fibonacci groups, Proc. London Math. Soc. (to appear).Google Scholar
(7) Miller, G. A., Groups generated by n operators each of which is the product of the n-1 remaining ones, Amer. J. Math. 30 (1908), 93–98.CrossRefGoogle Scholar