No CrossRef data available.
Article contents
A DYNAMICAL SYSTEM PROOF OF NIVEN’S THEOREM AND ITS EXTENSIONS
Part of:
Algebraic number theory: global fields
Elementary classical functions
Polynomials and matrices
Smooth dynamical systems: general theory
Published online by Cambridge University Press: 21 June 2023
Abstract
Niven’s theorem asserts that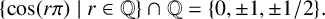 
$\{\cos (r\pi ) \mid r\in \mathbb {Q}\}\cap \mathbb {Q}=\{0,\pm 1,\pm 1/2\}.$ In this paper, we use elementary techniques and results from arithmetic dynamics to obtain an algorithm for classifying all values in the set 
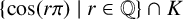$\{\cos (r\pi ) \mid r\in \mathbb {Q}\}\cap K$, where K is an arbitrary number field.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 109 , Issue 1 , February 2024 , pp. 138 - 151
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The second author is supported by National Research Council of Thailand (NRCT) under the Research Grant for Mid-Career Scholar no. N41A640153. The third author acknowledges funding by the Office of the Permanent Secretary, Ministry of Higher Education, Science, Research and Innovation (OPS MHESI), Thailand Science Research and Innovation (TSRI) and King Mongkut’s University of Technology Thonburi (Grant No. RGNS 64-096).
References
Bach, E. and Shallit, J., Algorithmic Number Theory, Volume 1: Efficient Algorithms, Foundations of Computing Series (MIT Press, Cambridge, MA, 1996).Google Scholar
Billal, M. and Riasat, S., Integer Sequences: Divisibility, Lucas and Lehmer Sequences (Springer, Singapore, 2021).CrossRefGoogle Scholar
Bousch, T., Sur quelques problèmes de dynamique holomorphe, PhD Thesis, Paris 11, 1992.Google Scholar
Canci, J. K. and Paladino, L., ‘Preperiodic points for rational functions defined over a global field in terms of good reduction’, Proc. Amer. Math. Soc. 144(12) (2016), 5141–5158.CrossRefGoogle Scholar
Flynn, E. V., Poonen, B. and Schaefer, E. F., ‘Cycles of quadratic polynomials and rational points on a genus-2 curve’, Duke Math. J. 90(3) (1997), 435–463.CrossRefGoogle Scholar
Ih, S.-I. and Tucker, T. J., ‘A finiteness property for preperiodic points of Chebyshev polynomials’, Int. J. Number Theory 6(5) (2010), 1011–1025.CrossRefGoogle Scholar
Jahnel, J., ‘When is the (co)sine of a rational angle equal to a rational number?’, Preprint, 2010, arXiv:1006.2938.Google Scholar
Lehmer, D. H., ‘Questions, discussions, and notes: a note on trigonometric algebraic numbers’, Amer. Math. Monthly 40(3) (1933), 165–166.CrossRefGoogle Scholar
Morton, P., ‘On certain algebraic curves related to polynomial maps’, Compos. Math. 103(3) (1996), 319–350.Google Scholar
Morton, P., ‘Arithmetic properties of periodic points of quadratic maps. II’, Acta Arith. 87(2) (1998), 89–102.CrossRefGoogle Scholar
Morton, P. and Silverman, J. H., ‘Rational periodic points of rational functions’, Int. Math. Res. Not. IMRN 1994(2) (1994), 97–110.CrossRefGoogle Scholar
Niven, I., Irrational Numbers, The Carus Mathematical Monographs, 11 (Mathematical Association of America; distributed by John Wiley, New York, 1956).CrossRefGoogle Scholar
Northcott, D. G., ‘Periodic points on an algebraic variety’, Ann. of Math. (2) 51 (1950), 167–177.CrossRefGoogle Scholar
Paolillo, B. and Vincenzi, G., ‘An elementary proof of Niven’s theorem via the tangent function’, Internat. J. Math. Ed. Sci. Tech. 52(6) (2021), 959–964.CrossRefGoogle Scholar
Paolillo, B. and Vincenzi, G., ‘On the rational values of trigonometric functions of angles that are rational in degrees’, Math. Mag. 94(2) (2021), 132–134.CrossRefGoogle Scholar
Poonen, B., ‘The classification of rational preperiodic points of quadratic polynomials over Q: a refined conjecture’, Math. Z. 228(1) (1998), 11–29.CrossRefGoogle Scholar
Samart, D., ‘On an extension of Niven’s theorem’, Internat. J. Math. Ed. Sci. Tech., to appear. Published online (1 August 2022).Google Scholar
Silverman, J. H., The Arithmetic of Dynamical Systems, Graduate Texts in Mathematics, 241 (Springer, New York, 2007).CrossRefGoogle Scholar
Stoll, M., ‘Rational 6-cycles under iteration of quadratic polynomials’, LMS J. Comput. Math. 11 (2008), 367–380.CrossRefGoogle Scholar
Vivaldi, F. and Hatjispyros, S., ‘Galois theory of periodic orbits of rational maps’, Nonlinearity 5(4) (1992), 961–978.CrossRefGoogle Scholar
Walde, R. and Russo, P., ‘Rational periodic points of the quadratic function
${Q}_c(x)={x}^2+c$
’, Amer. Math. Monthly 101(4), 318–331.Google Scholar
${Q}_c(x)={x}^2+c$
’, Amer. Math. Monthly 101(4), 318–331.Google ScholarZhang, R., ‘The
${abcd}$
conjecture, uniform boundedness, and dynamical systems’, Preprint, 2022, arXiv:2206.09725.Google Scholar
${abcd}$
conjecture, uniform boundedness, and dynamical systems’, Preprint, 2022, arXiv:2206.09725.Google Scholar