1 Introduction

In alternating current power applications we often have to do with conditions in which the frequency of a supply voltage is not constant but changes smoothly. This is attributable to a deliberate frequency change, for example during the frequency starting of ac motor drives as well as in the conditions of an external effect acting on a system, and an example of such case is an electric grid in which the influence of wind driven generators is strong. The common expectation is that when the supply voltage frequency variations occur, the current frequency in the respective circuit follows strictly the frequency of the voltage. But it is not the case. The current frequency changes in a different manner than the case of the frequency of the supply voltage, and in a general way one can say the variations in the current frequency amplify the changes of frequency of the supply voltage. For example in a case of voltage frequency increase, the frequency of the current in a circuit increases much more than this of the voltage and the phenomenon of current frequency overshoot is observed. This observation comes the result of the research presented in this paper and it was not, as far as the author knows, presented earlier. It is so probably, because in most applications, when the voltage frequency variations occur, the effort focuses on counteracting them by the voltage frequency control. The problem is related to the Fresnel integral [1,2,3,4], which originated in optics, and in the case of electrical power engineering this integral could be applied in some specific voltage frequency functions \({f}_{v}\left(t\right)\). The outlined problem is solved and presented in this paper in an analytical way. The frequency function \({f}_{v}\left(t\right)\) of a supply voltage is introduced and the frequency \({f}_{c}\left(t\right)\) of the resulting current is found. Section 2 shows that for some kind of voltage frequency functions \({f}_{v}\left(t\right)\) electric current could be solved analytically by use of the Fresnel integral, while generally the current course could be solved by the numerical computation of respective ordinary differential equations. But regardless of current waveform finding, it is possible to find analytical solution for the fc(t) frequency of the current if only the supply voltage frequency function \({f}_{v}\left(t\right)\) is a continuous function. This is discussed in Sect. 3. In Sect. 4 the solution of the inverse problem is presented. It is the case when we require some frequency \({f}_{cr}\left(t\right)\) of the current as the output and we need to find what kind of the voltage frequency \({f}_{vr}\left(t\right)\) will provide such an effect. In this section an ordinary differential equation is developed with the purpose of solving this problem. All theoretical considerations are illustrated in the paper by three exemplary functions representing voltage frequency increase: linear, sinusoidal and exponential, but also a case of decrease of the voltage frequency is illustrated. The results are extensively illustrated to demonstrate various rates of frequency increase and to support the results obtained by the analytical solutions. With the purpose of achieving a practical effect, Sect. 5 presents a case study for an induction motor starting by the linear increase of frequency of supply voltage to demonstrate a rotational speed overshoot that happens as the result of 3-phase current frequency overshoot in the stator windings. Finally, Sect. 6 contains discussion of the results in respect to the related problems presented in literature and open fields for further studies, and Sect. 7 presents main conclusions of this research.

2 R,L circuit supplied by changing frequency voltage

A simple R,L circuit presented in Fig. 1 forms a sufficient structure to demonstrate all major effects of changing frequency of the voltage supply. The supply voltage is

Fig. 1
figure 1

Electric R,L circuit applied for further investigations

Full size image
$$u(t)={U}_{m}\cdot \mathrm{sin}(2\pi {f}_{v}\left(t\right)\cdot t)$$
(1)

Electric current in this circuit, after an assumption is made to adopt zero initial condition for electric current, is calculated by integrating the following differential equation

$$\mathrm{i}(\mathrm{t})=\frac{1}{L}{\int }_{0}^{t}({U}_{m}\mathrm{sin}(2\pi {f}_{v}\left(\tau \right)\cdot \tau )-Ri(\tau )){d}\tau$$
(2)

To illustrate the problem of the current frequency, the integral of the supply voltage is analyzed, as it plays a key role in solution of (2)

$${\int }_{0}^{t}{U}_{m}\mathrm{sin}(2\pi {f}_{v}\left(\tau \right)\cdot \tau )\mathrm{d}\tau$$
(3)

There is no general solution for integral (3) in standard mathematical functions, but there are solutions for some specific \({f}_{v}\left(\mathrm{t}\right)\), for example for \({f}_{v}\left(\mathrm{t}\right)\) represented by a simple polynomial of t. These solutions employ special functions such as the Fresnel integral. First, three selected exemplary frequency functions will be considered: linear (4), sine-shaped (5) and exponential (6), where \(\varDelta f={f}_{k}-{f}_{0}\) means change of frequency between initial f0 and final fk point of frequency function \({f}_{v}\left(t\right)\).

The linear frequency function is:

$$\left\{\begin{array}{cc}{f}_{v1}\left(t\right)={f}_{0}+\varDelta f\frac{t}{T}& \quad for\ t\le T\\ {f}_{k} & for\ t>T\end{array}\right\}$$
(4)

with: \(\varDelta f={f}_{k}-{f}_{0}\)

The sine-shaped frequency function is:

$$\left\{\begin{array}{cc}{f}_{v2}\left(t\right)={f}_{0}+\varDelta f\mathrm{sin}(\frac{\pi }{2}\frac{t}{T} )& \quad for\ t\le T\\ {f}_{k} & for\ t>T\end{array}\right\}$$
(5)

And finally the exponential frequency function is:

$${f}_{v3}\left(t\right)={f}_{0}+\varDelta f\left(1-{e}^{-\frac{t}{T}}\right)$$
(6)

Plots of these functions are presented in Fig. 2.

Fig. 2
figure 2

Voltage frequency functions: linear \({f}_{v1}\), sinusoidal \({f}_{v2}\) and exponential \({f}_{v3}\)

Full size image

For the linear increase function (4) the integral

$${If}_{v1}\left(t\right)={\int }_{0}^{t}\left(\mathrm{sin}2\pi \left({f}_{0}+\varDelta f\frac{\tau }{T}\right)\tau \right) d\tau$$

could be rewritten in a more concise form

$${If}_{v1}\left(t\right)={\int }_{0}^{t}sin(a\tau +b{\tau }^{2})d\tau$$
(7)

with: \(a=2\pi {f}_{0}\)    \(b=2\pi \frac{\varDelta f}{T}\)

The solution of integral (7) is

$$If_{v1} \left( t \right) = \sqrt {\frac{\pi }{2b}} \left[ {cos\left( {\frac{{a^{2} }}{4b}} \right)S\left( {\frac{a + 2bt}{{\sqrt {2\pi b} }}} \right) - sin\left( {\frac{{a^{2} }}{4b}} \right)C\left( {\frac{a + 2bt}{{\sqrt {2\pi b} }}} \right)} \right]\;\;{\text{for}}\;\;t \le T$$
(8)

where: \(\mathrm{S}\left(\mathrm{t}\right)\) and \(\mathrm{C}\left(\mathrm{t}\right)\) are the Fresnel sine and cosine integrals, respectively [1,2,3,4]. From (8) one can compute an integral of voltage for linear increase of frequency, according to \({\mathrm{f}}_{{v}1}\) function.

Besides, it is necessary to explain here that continuous frequency increase lines in Fig. 4 were derived in a numerical way on the basis of the integral of voltage waveforms, in the manner similar as in Fig. 3, using the formula

Fig. 3
figure 3

Solution of the voltage integral (7), in case of linear increase of frequency, from \({\mathrm{f}}_{0}=0\ (\mathrm{Hz})\) to \({\mathrm{f}}_{{k}}=50\ (\mathrm{hz})\), \(\mathrm{T}=0.6\ (\mathrm{s})\) by the use of Fresnel integral

Full size image
$$f=\frac{1}{2({t}_{i+1}-{t}_{i})}$$
(9)

where \({\mathrm{t}}_{{i}+1}-{\mathrm{t}}_{{i}}\) is the half wave time, that represents the period between consecutive maximum and minimum (or reverse) value of a voltage course. The numerical method for finding an actual current frequency is necessary, because this frequency is entangled in a way that makes its explicit solution impossible. From Fig. 4 one can see that maximum overshoot of the frequency takes place at the end of the line, and it is equal to

Fig. 4
figure 4

Frequency increase of voltage integral (8), for \({\mathrm{f}}_{0}=0, 10, 20 , 30, 40\ (\mathrm{Hz})\), \({\mathrm{ f}}_{{k}}=50\ (\mathrm{Hz})\), \(\mathrm{T}=0.6\ (\mathrm{s})\)

Full size image
$${\varDelta f}_{dmax}={f}_{k}-{f}_{0}=\varDelta f$$
(10)

The same result for the linear increase in function \({f}_{v1}\left(t\right)\) will be presented in an analytical form later. The exemplary shape of the current for linear increase of voltage frequency is presented in Fig. 5.

Fig. 5
figure 5

Electric current in R,L circuit for linear voltage frequency increase, according to (4)

Full size image

The effects of the voltage integral and frequency overshoot will be presented in numerical way for the sine-shaped (5) and exponential (6) frequency functions, on the basis of the computed current waveforms in the R,L circuit (Fig. 1). This is executed in such a manner since there are no analytical solutions of voltage integral for these kind of functions. In case of the sine-shaped frequency function (5) exemplary result of electric current in the circuit is presented in Fig. 6. Apparently, it is possible to resolve these functions (5,6) into power serious, and then apply the Fresnel integral to a limited number of expressions, but this way is not much effective. All computations concerning this circuit are carried out for \(R=10 \left[\varOmega \right], L=0.03 [H]\), \({U}_{m}=230\sqrt{2} \left[V\right],\) but it is necessary to explain that the frequency of the computed current is not sensitive to these parameters. It has been tested numerically in a wide range of the time constant \({T}_{p}=\frac{L}{R}={10}^{-5}\dots {10}^{5}\ \text{ [s]}\). All numerical computations in this research were carried out by the use of Maple math software, and specifically differential equations were solved by application of the desolve procedure intended also for stiff systems.

Fig. 6
figure 6

Electric current in R,L circuit for sinusoidal shape of voltage frequency increase

Full size image

Figure 7 shows how the frequency of electric current \({f}_{c}\left(t\right)\) goes over the frequency of voltage (dotted line for \({f}_{0}=0\)) in the R,L circuit in case of sinusoidal voltage frequency increase from initial \({f}_{0}\) to the final \({f}_{k}\). The subsequent figure, i.e. Figure 8 shows the dynamic overshoot of current frequency \({\varDelta f}_{d}={f}_{c}\left(t\right)-{f}_{v}\left(t\right)\), over the \({f}_{v2}\left(t\right)\) voltage frequency, and the static overshoot of current frequency \({\varDelta f}_{s}={f}_{c}\left(t\right)-{f}_{k}\), over the final \({f}_{k}\) voltage frequency. The maximum value of overshoot is proportional to difference of \({\varDelta f=f}_{k}-{f}_{0}\), and this proportion will be explained later in the paper. The similar characteristics will be demonstrated for the \({f}_{v3}\left(t\right)\) frequency function, which is exponential. Figure 9 presents electric current in R,L circuit, while the supply voltage frequency increases exponentially, and Fig. 10 shows electric current frequency for \({f}_{0}=0, 10, 20 , 30, 40\text{ (Hz)}\) with this kind of supply. Figure 11 shows dynamic overshoot \({\varDelta f}_{d}\) of current frequency \({f}_{c3}\left(t\right)\), that is surplus of current frequency over voltage frequency \({f}_{v3}\left(t\right)\), and Fig. 12 shows static overshoot \({\varDelta f}_{s}\) of current frequency \({f}_{c3}\left(t\right)\), which is the surplus over final \({f}_{k}\) frequency.

Fig. 7
figure 7

Frequency of the voltage (the dotted line, \({f}_{0}=0\text{ (Hz)})\) and dynamic frequency of current \({f}_{c}(t)\) for sinusoidal increase of voltage frequency from \({f}_{0}=0, 10, 20 , 30, 40\text{ (Hz)}\) to \({f}_{k}=50\text{ (Hz)}\)

Full size image
Fig. 8
figure 8

Dynamic \({\varDelta f}_{d}\) – dash lines, and static \({\varDelta f}_{s}\) – solid lines, overshoot of frequency of current, for sinusoidal increase of voltage frequency from \({f}_{0}=0, 10, 20 , 30, 40\text{ (Hz)}\) to \({f}_{{k}}=50\text{ (Hz)}\)

Full size image
Fig. 9
figure 9

Electric current in R,L circuit for exponential frequency increase of voltage; \(T=0.075\text{ s}\)

Full size image
Fig. 10
figure 10

Frequency of the voltage (dotted line, \({f}_{0}=0\text{ (Hz)})\) and dynamic frequency \({f}_{c3}\left(t\right)\) of current for exponential increase of voltage frequency from \({f}_{0}=0, 10, 20 , 30, 40\text{ (Hz)}\) to \({f}_{{k}}=50\text{ (Hz)}\); \(T=0.075 \text{ s}\)

Full size image
Fig. 11
figure 11

Dynamic overshoot of frequency of currents \({\varDelta f}_{d}\), for exponential increase of voltage frequency  \({f}_{v3}\left(t\right)\), from \({f}_{0}=0, 10, 20 , 30, 40{\text{ (Hz)}}\) to \({f}_{k}=50{\text{ (Hz)}}\); \(T=0.075\text{ (s)}\)

Full size image
Fig. 12
figure 12

Static overshoot of frequency of currents \({\varDelta f}_{s}\), for exponential increase of voltage frequency \({f}_{v3}\left(t\right)\) from \({f}_{0}=0, 10, 20 , 30, 40\ \left(\text{Hz}\right)\) to \({f}_{k}=50\ \left(\text{Hz}\right)\); \(T=0.075\ \text{(s)}\)

Full size image

A summary of the results for these computations are presented in Table 1 for the sinusoidal frequency increase (5) of the voltage, and in Table 2 for the exponential frequency increase (6) of the voltage. The results for the linear voltage frequency increase (4) are not summarized in a table, because in that case the instantaneous frequency of the current is simply doubled in respect to voltage frequency \({f}_{v1}\left(t\right)\) and increases linearly (Fig. 4).

Table 1 Characteristics of current frequency in the case of sinusoidal increase of voltage frequency
Full size table
Table 2 Characteristics of current frequency in the case of exponential increase of voltage frequency
Full size table

An interesting result from the Table 1 is that the ratio of the maximum dynamic overshoot of current frequency \({f}_{{d max}}\), in respect to \(\varDelta f={f}_{k}-{f}_{0}\) is constant. Similar observation concerns static overshoot of current frequency Δ \({f}_{{s} \mathrm{max}}\)/\(\varDelta f\). Table 2 contains a collection of quite similar results, but for an exponential increase of the voltage frequency.

The effects of the current frequency changes, in case of decreasing supply voltage frequency, are in principle similar to those when the voltage frequency increase. It means that the frequency of the current \({f}_{c}\left(t\right)\) goes below the frequency of supply voltage \({f}_{v}\left(t\right)\) and the overshoot of the current frequency is negative. This is presented in Figs. 13, 14 and Fig. 15 for the initial voltage frequency \({f}_{0}=60, 50, 40 , 30\ (\mathrm{Hz})\) and the final voltage frequency \({f}_{k}=10\ (\mathrm{Hz})\). Figure 13 presents the electric current in the circuit for the case of \({f}_{0}= 60\ (\mathrm{Hz})\), \({f}_{{k}}=10\ (\mathrm{Hz})\). It shows very low frequency in the middle of the course and its gradual increase to final \({f}_{k}=10\ (\mathrm{Hz})\). A collection of graphic results for this example of decreasing voltage frequency along the exponential \({f}_{v}\left(t\right)\) curves are presented in Fig. 14 and in Fig. 15, to show how much voltage frequencies exceed those of the current frequencies. Numerical results for this case, are presented in Table 3, and we can see that the ratios Δ \({f}_{d max}\)/\(\varDelta f\) and Δ \({f}_{{s} \mathrm{max}}\)/\(\varDelta f\) have the same values as in case of increasing voltage frequency, presented in Table 2. The interesting result is that for the exponential function of the voltage frequency changes, we receive dynamic overshoot ratio equal to Δ \({f}_{d max}\)/\(\varDelta f\cong 0.368\), which offers a suitable approximation of the value  \({ e}^{-1}\), and a static overshoot ratio Δ \({f}_{{s max}}\)/\(\varDelta f\cong 0.135\), which is a good approximation of  \({e}^{-2}\). These two results confirm the theory presented further in the next paragraph.

Fig. 13
figure 13

Electric current in R,L circuit for exponential frequency decrease from \({f}_{0}= 60{\text{ (Hz)}}\) to \({f}_{{k}}=10{\text{ (Hz)}}\); \(T=0.075\ \text{(s)}\)

Full size image
Fig. 14
figure 14

Presentation of exponential decrease of voltage frequency \({f}_{v3}\left(t\right)\), from \({f}_{0}=60, 50, 40, 30{\text{ (Hz)}}\) to \({f}_{k}=10{\text{ (Hz)}}\) – dash lines, and respective frequencies of current \({f}_{c3}\left(t\right)\) – solid lines; \(T=0.075\ \text{(s)}\)

Full size image
Fig. 15
figure 15

Overshoot of frequency \({f}_{c3}\left(t\right)\) of current, for exponential decrease (\(T=0.075 \text{ (s)}\)) of voltage frequency\({f}_{v3}\left(t\right)\), from \({f}_{0}=60, 50, 40 , 30{\text{ (Hz)}}\) to final \({f}_{{k}}=10{\text{ (Hz)}}.\) Static overshoot \({\varDelta f}_{s}\) – solid lines, and dynamic \({\varDelta f}_{d}\) – dash lines

Full size image
Table 3 Characteristics of current frequency for exponential decrease of voltage frequency from \({f}_{0}\) to \({f}_{k}=10\ (\mathrm{Hz})\)
Full size table

The next issue that will be discussed here involves the case in which the final frequency is zero, or negative. One example, that deals with such a case is presented in Figs. 16 and 17. There, the voltage frequency \({f}_{{v}}(t)\) decreases exponentially from \({f}_{0}= 40{\text{ (Hz)}}\) to \({f}_{k}=0{\text{ (Hz)}}\), and current frequency \({f}_{{c}}(t)\), in its dynamic course, goes below zero and then approaches zero from the negative side of the time axis. In a single phase system this does not mean that the frequency is negative, as it just passes zero and changes phase (see Fig. 16). But in the three phase system negative frequency means change of sequence of phases.

Fig. 16
figure 16

Electric current in R,L circuit for exponential voltage frequency decrease (\(T=0.075 \text{ (s)}\)) from \({f}_{0}= 40{\text{ (Hz)}}\) to \({f}_{{k}}=0{\text{ (Hz)}}\)

Full size image
Fig. 17
figure 17

Frequency of the voltage \({f}_{v3}(t)\) and dynamic frequency of current \({f}_{c3}\left(t\right),\) for exponential decrease (\(T=0.075 \text{ (s)}\)) of voltage frequency from \({f}_{0}=40{\text{ (Hz)}}\) to \({f}_{k}=0{\text{ (Hz)}}\)

Full size image

3 Analytical solution for dynamic current frequency

The aim of this section is to find and present analytical solution of a current frequency \({f}_{{c}}(t)\) when a supply voltage frequency is given. The differential equation for the R,L circuit presented in Fig. 1, in case of linear parameters R,L is quite simple

$$u\left(t\right)=U(t)\mathrm{sin}\left(2\pi {f}_{v}\left(t\right)\cdot t\right)=Ri\left(t\right)+L \frac{d}{dt}i\left(t\right)$$
(11)

As it was mentioned, analytical solution of (11) does not exist for an arbitrary \({f}_{v}\left(t\right)\) frequency function, but it is still possible to establish a frequency \({f}_{c}\left(t\right)\) of the solution (current) in a general form. To find it, let us transform differential Eq. (11) to the complex form, by introducing

$$u\left( t \right) = {\text{Im}} \left\{ {\left. {U\left( t \right)e^{j\omega t} } \right\}} \right.\;\;\;\;i\left( t \right) = {\text{Im}} \left\{ {I\left. {\left( t \right)e^{j\rho } } \right\}} \right.$$
(12)

with: \(\omega =\omega \left(t\right)=2\pi {f}_{v}(t)\)\(\rho =\rho (t)\) – current phase angle (see Fig. 18).

Fig. 18
figure 18

Illustration of the voltage and current vectors on a complex plane in respect to the stationary frame α,β

Full size image

and: \(U(t)\) – amplitude of the supply voltage \(I\left(t\right)>0\) – amplitude of the current.

The differential Eq. (11), after introducing complex variables, takes the form

$$U\left(t\right){e}^{j\left(\omega t-\rho \right)}=RI\left(t\right)+L\dot{I}\left(t\right)+j\dot{\rho }I(t)L$$
(13)

with: \(\dot{I}=\frac{d}{dt}I \quad \dot{\rho }=\frac{d}{dt}\rho\)

The complex Eq. (13) with the two variables \(I(t)\) and \(\rho (t)\), can be arranged as a set of two equations

$$\dot{I}\left( t \right) = \frac{U\left( t \right)}{L}\cos \left( {\omega t - \rho } \right) - \frac{R}{L}I\left( t \right)\;\;\;\dot{\rho } = \frac{U}{LI\left( t \right)}\sin \left( {\omega t - \rho } \right)\;\;\;I\left( t \right) > 0$$
(14)

The solution to this system of differential Eq. (14) allows us to find current phase angle \(\rho\), which is presented in Fig. 19. The small deflections of the \(\rho\) curves from a straight line are responsible for the differences between voltage and current frequencies. The angle \(\left(\omega t-\rho \right)\) is quasi-constant, in comparison with the angle \(\omega t\), because it changes less than 1 rad during the whole period T of the voltage frequency changes. Even for a short time like T = 0.05 (s), this approximation \(\left(\omega t-\rho \right)\cong const\) is quite correct, and it is presented in Fig. 20. In fact, this difference denotes the power factor angle φ for the circuit. It changes with frequency, but this change is much limited. On the basis of the equation:

Fig. 19
figure 19

Rho angle of the rotating electric current vector, obtained as a solution of transformed (14) equations for R,L circuit, in case of voltage \({f}_{v}(t)\) frequency increase from \({f}_{0}=0, 15, 30 , 45 {\text{ (Hz)}}\) to \({f}_{k}=60 {\text{ (Hz)}}\)

Full size image
Fig. 20
figure 20

Results of solution of the equation \(\mathrm{\varphi }=\left(\omega t-\rho \right)\) for the sine-shaped voltage frequency \({f}_{v2}(t)\) increase from \({f}_{0}=0, 10, 20 , 30, 40 {\text{ (Hz)}}\) to \({f}_{k}=50 {\text{ (Hz)}}\). The period of increase is: T = 0.6 (s) or a, and T = 0.05 (s) for b

Full size image
$$\mathrm{\varphi }=\left(\omega t-\rho \right)\cong \mathrm{const}$$
(15)

the time derivative can be calculated, and it gives a very good approximation of the current angular frequency

$$\dot{\rho }=\dot{\omega }t+\omega$$
(16)

From (16) we receive

$${f}_{c}\left(t\right)=\frac{\dot{\rho }}{2\uppi }={f}_{v}\left(t\right)+t\frac{d}{\mathrm{dt}}{f}_{v}\left(t\right)$$
(17)

which is the solution for the current frequency.

Applying (17) we can find current frequency for each of the three specific cases of supply voltage frequency \({f}_{g}(t)\). For the linear increase (4) it is

$$\left\{\begin{array}{cc}{f}_{c1}\left(t\right)={f}_{0}+2\cdot \varDelta f\frac{t}{T}& for\ t\le T\\ {f}_{k} & for t>T\end{array}\right\}$$
(18)

– so the dynamic overshoot of current frequency is \(\varDelta f\frac{t}{T}\), and its maximum is  \(\varDelta f\). For the sinusoidal increase (5) of voltage:

$$\left\{\begin{array}{cc}{f}_{c2}\left(t\right)={f}_{0}+\varDelta f\left[\begin{array}{c}\mathrm{sin} \left(\frac{\pi }{2}\frac{t}{T} \right)+\\ +\frac{\pi }{2}\frac{t}{T}cos\left(\frac{\pi }{2}\frac{t}{T}\right)\end{array}\right]& for\ t\le T\\ {f}_{k} & for\ t>T\end{array}\right\}$$
(19)

- and the maximum of the dynamic overshoot of current frequency is \(\varDelta {f}_{d max}\cong 0.564 \varDelta f\)  for  \(t=2.15375\frac{T}{\pi }\)

- maximum of the static overshoot is:  Δ \({f}_{s max}\cong 0.392 \varDelta f\) for \(t=1.720667\frac{T}{\pi }\).

Finally, for exponential increase (6) of voltage frequency:

$${f}_{c3}\left(t\right)={f}_{0}+\varDelta f \left(1-\frac{T-t}{T}{e}^{-\frac{t}{T}}\right)$$
(20)

– and the maximum of the dynamic overshoot of current frequency is \(\varDelta{f}_{d max}\cong \varDelta f {e}^{-1}\) for  \(t=T\)

- maximum of the static overshoot is Δ \({f}_{s max}\cong \varDelta f {e}^{-2}\) for  \(t=2T\).

All these analytical results are derived from Eq. (17), and in that sense they are accurate, but we have to remember that Eq. (15) is not accurate, as it assumes that the phase shift \(\varphi\) is constant. Hence, in fact, the Eq. (15) constitutes the assumption for the theory presented in paragraphs 3 and 4. But in practice, the results based on the computer simulation using the differential equation in (11) and results obtained from Eqs. (17) to (19) do not differ noticeably.

4 Inverse problem: finding voltage frequency function \({{\varvec{f}}}_{\mathbf{v}\mathbf{r}}\) for required current frequency \({{\varvec{f}}}_{\mathbf{c}\mathbf{r}}\)

When a required current frequency \({f}_{{cr}}\) is given and we look for the \({f}_{{vr}}\) voltage frequency that fulfills that task, Eq. (17) becomes an ordinary differential equation that can be applied to solve the inverse problem:

$$\frac{{d}}{{d}t}\left({f}_{{vr}}\right)\cdot t+{f}_{{vr}}={f}_{{cr}}$$
(21)

The solution of (21) takes the following form

$${f}_{{vr}}=\frac{1}{t}{\int }_{1}^{t}{f}_{{cr}}(\tau )d\tau +\frac{c}{t}$$
(22)

where c is an arbitrary constant and the lower limit of the integral can take the form of any nonzero value. Now, let us treat three frequency functions (4)…(6), which originally represented the voltage frequency functions \({f}_{{v}}\) of a linear, sinusoidal and exponential frequency increase, as the required frequency functions \({f}_{{cr}}\) for the current in a circuit. By the use of (22) we can find voltage frequency functions \({f}_{{vr}}\) to receive the required current frequencies \({f}_{{cr}}\). For the linear increase of current frequency, the result is quite obvious:

$${f}_{{vr}1}\left(t\right)={f}_{0}+\varDelta f \frac{t}{2T}$$
(23)

as it divides the slope of frequency increase by 2. For the sinusoidal current frequency increase from (22) we receive:

$${f}_{{vr}2}\left(t\right)={f}_{0}-\varDelta f \frac{2}{\pi }\frac{T}{t}\mathrm{cos} \left(\frac{\pi }{2}\frac{t}{T} \right) \:\:\:\:\: t>0$$
(24)

and finally for exponential current frequency increase:

$${f}_{{vr}3}\left(t\right)={f}_{0}+\varDelta f \frac{T}{t}{e}^{-\frac{t}{T}}\:\:\:\:\:\:\: t>0$$
(25)

For sinusoidal (24) and exponential (25) frequency increase, both \({f}_{cr}\) and \({f}_{vr}\) functions are presented in Fig. 21.

Fig. 21
figure 21

Illustration of the inverse problem solution: required current frequency functions \({f}_{cr}\) (as output – solid lines), and voltage frequency functions \({f}_{vr}\) (as input–dash lines) – for \({f}_{0}=0, 10, 20 , 30, 40 {\text{ (Hz)}}\) and \({f}_{k}=50{\text{ (Hz)}}.\) The case presented in Fig. 21. a concerns sinusoidal frequency increase (\(T=0.6 \text{(s)}\)), and in Fig. 21. b concerns exponential frequency increase (\(T=0.075 \text{(s)}\))

Full size image

5 Case study for an induction motor starting

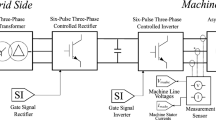
To illustrate this problem in more practical conditions, a computer simulation for an induction motor supplied by 3- Level Diode-Clamped Inverter (3-LDCI) is presented in this paragraph. The induction machine: 5.5 [kW], 400 [V], 50 (Hz), 11.5 [A], p = 3 (974 rev/min) gives a typical 3- phase motor design. This drive, with linearly increasing load torque and external inertia, which was four times the rotor’s inertia, started with a linear increase of the voltage frequency from 20 (Hz) to final 50 (Hz) in 1.1 [s]. The control of the inverter takes into account the variable \({f}_{v}\) frequency throughout the process of computing the actual period of a pulse, with a constant number of pulses, within an accordingly variable ‘period’ of the supply voltage. Also, the actual voltage space-vector position has been computed accounting for the \({f}_{v}\)(t) frequency function in the form that is presented in Fig. 22. The actual value of supply voltage during starting course has been computed using a corrected U/f formula, which takes into account higher output frequency than the one given by the frequency increase curve presented in Fig. 22. The general results of this exemplary simulations are presented in Figs. 23, 24 and 25. In Fig. 24 we can see one of the phase currents with clearly increasing frequency until 1.1 [s] followed by a serious disruption after frequency function switches to the constant frequency of 50 (Hz).

Fig. 22
figure 22

Linear ramp of voltage frequency increase during induction motor drive starting

Full size image
Fig. 23
figure 23

Phase current of the induction motor during the frequency starting with the linear frequency increase

Full size image
Fig. 24
figure 24

Electromagnetic torque of the motor during the frequency starting with the linear frequency increase

Full size image
Fig. 25
figure 25

Rotational speed of the motor during the frequency starting with the linear frequency increase

Full size image

In Fig. 24 we can see that the course of electromagnetic torque runs in a very smooth shape until the sharp disruption occurs after 1.1 [s], when the abrupt frequency change takes place. The maximum negative torque value, about -230 [Nm], is 4.15 multiple of the nominal torque value, which is realistic. But we have to consider that the mathematical model of the induction motor applied here does not take into account magnetic saturation, and all results concerning high current values are affected by greater error values. Next, in Fig. 25 rotational speed of the drive clearly shows the effect of the frequency overshoot. The maximum value of speed is about 1550 (rev/min), while the synchronous speed at 50 (Hz) is equal to 1000 (rev/min). According to (18), which concerns linear voltage frequency increase, the final \({f}_{c}\) frequency in the presented case should be 80 (Hz), which gives 1600 (rev/min) speed of the magnetic field rotation. The speed difference between the magnetic field and the rotor speed gives s = 3.1% of the slip value, which is quite convincing. Finally Fig. 26 presents a short segment of the waveform of the phase current and motor clamps voltage. The motor clamps voltage curves are not drawn very precisely because of the graphic limitations, but the applied basic time step for computations was 2.0E-5 [s], allowing for the high switching frequency. Generally, this example shows that the linear frequency increase is not the best option, due to the considerable current frequency overshoot and a substantial dynamic disruption after the point of the sharp frequency slope change. It seems that the best option should be exponential voltage frequency increase, being a soft curve of change. However, this example does not include any rotor speed regulation during starting course, acting on the voltage frequency curve, which can introduce substantial difference in the operation of the drive.

Fig. 26
figure 26

Motor’s clamps voltage and phase current (multiplied by 20) at the final stage of the starting course: \({f}_{v}\) =45 (Hz), \({f}_{c}\) =72.0 (Hz), n = 1420 (rev/min)

Full size image

6 Discussion

The problem discussed here involves a difference between the frequency of the supply voltage and the frequency of the resulting current, and the examples when voltage frequency changes smoothly, are encountered in many applications and should be examined. Originally the similar problem was found in optics and it was addressed by the Fresnel integral. The Fresnel integral allows to integrate sinusoidal (cosine) functions in cases in which their pulsatance is not constant but it forms a time dependent polynomial. The technological applications of variable frequency in electrical power engineering came much later as a result development of power electronics. Variable frequency in power applications occurs as a result of the deliberate action such as in the case of ac motor drives starting and regulation, but it can also be recorded as a consequence of an external influence acting on a system, like in the case wind power generation. In the first case, when we start ac motor by means of increasing frequency [5,6,7,8,9,10,11], an overshoot of rotational speed takes place and it is counteracted by a speed control [12,13,14]. This problem applies also to zero voltage switching of the invertors that supply variable frequency drives [15,16,17]. In that case when the frequency of the voltage varies, the switching instant must be controlled by the zero current value, which is different of the zero voltage instant. The second field of applications, in which variable voltage frequency occurs is the case of grids with a large component of the wind power generation [18,19,20]. An effort is directed at minimizing voltage fluctuations [21,22,23,24,25,26] but this generally happens without knowledge whether current fluctuations in loads are significantly deeper then these of the supply voltage. The same problem should be investigated from the point of view of standards for power energy generation and consumption [27,28,29]. Standards should take into account that a deviations of the voltage frequency from nominal value in a grid have more significant impact on load currents than proportional. There are also other fields in which ‘frequency coupling’ [30,31,32,33] is reported as well as current frequency deviations (noise) are counteracted or mitigated [19, 34,35,36]. These are the areas to study by the respective specialists that should strive to see how much the inconsistency of a supply voltage frequency and resulting current frequency influence an operation of the system. It seems that the phenomenon of voltage and current inconsistency in the case of the supply voltage varying smoothly, was not noticed and discussed until now. All the papers cited above deal with a changing voltage frequency in various applications and its outcomes, but do not notice that the currents frequency changes are not the same as these of the voltage. It seems that all research effort was concentrated on control of voltage frequency [26, 37], (or speed) which overrides the natural tendency of current frequency changes. The studies of the phenomenon reported in this paper should look into the cases of the abovementioned applications, and possibly others, in which the ‘overshoot’ of current frequency is really meaningful, and find what kind of improvements could be done in particular control systems.

7 Conclusions

The main finding of this paper is that in a circuit supplied by sinusoidal voltage, with the frequency of this voltage varying smoothly to follow some continuous function \({f}_{v}(t)\), the frequency \({f}_{c}(t)\) of the current changes in a different manner than this of the voltage, and generally this frequency fortifies the tendency of the changes in voltage frequency. It means that if the voltage frequency increases following \({f}_{v}\)(t) function, the current frequency \({f}_{c}(t)\) increases even higher, and overshoot of current frequency over expected final frequency \({f}_{k}\), is observed. This can be seen from the integral (3) of voltage. This integral could be solved in standard mathematical functions only for some \({f}_{v}(t)\) frequency functions, and in such as case Fresnel integral functions are employed. For other \({f}_{v}(t)\) functions only numerical solutions exist. The current frequency \({f}_{c}(t)\), which is the output frequency of the system, does not depend on the circuit parameters or the period of time T in which these changes occur, as this frequency depends only on the shape of the \({f}_{v}(t)\) voltage frequency function. The function \({f}_{v}(t)\) has to be a continuous function only, and need not be monotony function, as it was the case for all examples presented here.

The next important conclusion is that the current frequency \({f}_{c}(t)\) is the same for a single circuit, multi-phase circuit or induction motor windings, and it depends solely on the integral of \({f}_{v}(t)\). This is confirmed in Paragraph 5 for more complex system for the induction motor drive frequency starting. Although there is no general solution of integral (3), it is still possible to establish a formula with the purpose of calculating the frequency of the current (integral of voltage) – see (17). This formula is derived under the assumption that the power factor angle φ = const, which is not true in general, but under such circumstances, Eq. (15) offers a very good approximation, as it is confirmed even while period T the of frequency change is very short. We can say that if T > 10/fk then the theory performs very well. The Eq. (17) offers one more possibility – to find such \({f}_{vr}(t)\), voltage frequency function, that the current frequency follows some required \({f}_{cr}(t)\) function. It is only necessary to solve the integral in (22).