Skip to main content
SpringerLink
Log in

In-plane dynamics of a fluid-conveying corrugated pipe supported at both ends

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

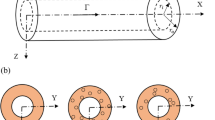
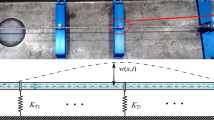
The dynamics and stability of fluid-conveying corrugated pipes are investigated. The flow velocity is assumed to harmonically vary along the pipe rather than with time. The dimensionless equation is discretized with the differential quadrature method (DQM). Subsequently, the effects of the mean flow velocity and two key parameters of the corrugated pipe, i.e., the amplitude of the corrugations and the total number of the corrugations, are studied. The results show that the corrugated pipe will lose stability by flutter even if it has been supported at both ends. When the total number of the corrugations is sufficient, this flutter instability occurs at a micro flow velocity. These phenomena are verified via the Runge-Kutta method. The critical flow velocity of divergence is analyzed in detail. Compared with uniform pipes, the critical velocity will be reduced due to the corrugations, thus accelerating the divergence instability. Specifically, the critical flow velocity decreases if the amplitude of the corrugations increases. However, the critical flow velocity cannot be monotonously reduced with the increase in the total number of the corrugations. An extreme point appears, which can be used to realize the parameter optimization of corrugated pipes in practical applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. PAÏDOUSSIS, M. P. and LI, G. X. Pipes conveying fluid: a model dynamical problem. Journal of Fluids and Structures, 7(2), 137–204 (1993)

    Article  Google Scholar 

  2. PAÏDOUSSIS, M. P. Fluid-Structure Interactions: Slender Structures and Axial Flow (Volume 1), Academic Press, London (2014)

    Google Scholar 

  3. PAÏDOUSSIS, M. P. Fluid-Structure Interactions: Slender Structures and Axial Flow (Volume 2), Academic Press, London (2016)

    Google Scholar 

  4. CHEN, S. Flow-induced in-plane instabilities of curved pipes. Nuclear Engineering and Design, 23, 29–38 (1972)

    Article  Google Scholar 

  5. PAÏDOUSSIS, M. P. and ISSID, N. T. Dynamic stability of pipes conveying fluid. Journal of Sound and Vibration, 33, 267–294 (1976)

    Article  Google Scholar 

  6. HOLMES, P. J. Pipes supported at both ends cannot flutter. Journal of Applied Mechanics, 45, 619–622 (1978)

    Article  MATH  Google Scholar 

  7. SEMLER, C., LI, G. X., and PAÏDOUSSIS, M. P. The non-linear equations of motion of pipes conveying fluid. Journal of Sound and Vibration, 169, 577–599 (1994)

    Article  MATH  Google Scholar 

  8. ZHANG, L. X. and HUANG, W. H. Analysis of nonlinear dynamic stability of liquid-conveying pipes. Applied Mathematics and Mechanics (English Edition), 23(9), 1071–1080 (2002) https://doi.org/10.1007/BF02437718

    Article  MATH  Google Scholar 

  9. MODARRES-SADEGHI, Y. and PAÏDOUSSIS, M. P. Nonlinear dynamics of extensible fluid-conveying pipes, supported at both ends. Journal of Fluids and Structures, 25, 535–543 (2009)

    Article  Google Scholar 

  10. ZHANG, Y. L. and CHEN, L. Q. Internal resonance of pipes conveying fluid in the supercritical regime. Nonlinear Dynamic, 67, 1505–1514 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  11. ZHANG, Y. L. and CHEN, L. Q. External and internal resonances of the pipe conveying fluid in the supercritical regime. Journal of Sound and Vibration, 332, 2318–2337 (2013)

    Article  Google Scholar 

  12. CHEN, L. Q., ZHANG, Y. L., ZHANG, G. C., and DING, H. Evolution of the double-jumping in pipes conveying fluid flowing at the supercritical speed. International Journal of Non-Linear Mechanics, 58, 11–21 (2014)

    Article  Google Scholar 

  13. MAO, X. Y., DING, H., and CHEN, L. Q. Steady-state response of a fluid-conveying pipe with 3:1 internal resonance in supercritical regime. Nonlinear Dynamics, 86, 795–809 (2016)

    Article  Google Scholar 

  14. WANG, L., JIANG, T. L., and DAI, H. L. Three-dimensional dynamics of supported pipes conveying fluid. Acta Mechanica Sinica, 33, 1065–1074 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  15. CZKO, J. and CZERWIŃKI, A. Nonlinear three-dimensional dynamics of flexible pipes conveying fluids. Journal of Fluids and Structures, 70, 235–260 (2017)

    Article  Google Scholar 

  16. WANG, Y. K., WANG, L., NI, Q., DAI, H. L., YAN, H., and LUO, Y. Y. Non-planar responses of cantilevered pipes conveying fluid with intermediate motion constraints. Nonlinear Dynamics, 93, 505–524 (2018)

    Article  Google Scholar 

  17. TAN, X., MAO, X. Y., DING, H., and CHEN, L. Q. Vibration around non-trivial equilibrium of a supercritical Timoshenko pipe conveying fluid. Journal of Sound and Vibration, 428, 104–118 (2018)

    Article  Google Scholar 

  18. YAN, H., DAI, H. L., NI, Q., WANG, L., and WANG, Y. K. Nonlinear dynamics of a sliding pipe conveying fluid. Journal of Fluids and Structures, 81, 36–57 (2018)

    Article  Google Scholar 

  19. XI, H. M., ZHANG, W., and YAO, M. H. Periodic and chaotic oscillations of the fluid conveying pipes with pulse fluid (in Chinese). Journal of Dynamics and Control, 6, 243–248 (2008)

    Google Scholar 

  20. DING, H., JI, J. C., and CHEN, L. Q. Nonlinear vibration isolation for fluid-conveying pipes using quasi-zero stiffness characteristics. Mechanical Systems and Signal Processing, 121, 675–688 (2019)

    Article  Google Scholar 

  21. ZHAO, X. Y., ZHANG, Y. W., DING, H., and CHEN, L. Q. Vibration suppression of a nonlinear fluid-conveying pipe under harmonic foundation displacement excitation via nonlinear energy sink. International Journal of Applied Mechanics, 10, 1–8 (2018)

    Google Scholar 

  22. YANG, T. Z., YANG, X. D., LI, Y., and FANG, B. Passive and adaptive vibration suppression of pipes conveying fluid with variable velocity. Journal of Vibration and Control, 20, 1293–1300 (2014)

    Article  MathSciNet  Google Scholar 

  23. GHAYESH, M. H., FAROKHI, H., and FARAJPOUR, A. Chaotic oscillations of viscoelastic microtubes conveying pulsatile fluid. Microfluidics and Nanofluidics, 22, 72 (2018)

    Article  Google Scholar 

  24. YANG, T. Z., JI, S. D., YANG, X. D., and FANG, B. Microfluid-induced nonlinear free vibration of microtubes. International Journal ofEngineering Science, 76, 47–55 (2014)

    Article  MATH  Google Scholar 

  25. KOLAHCHI, R. and BIDGOLI, A. M. M. Size-dependent sinusoidal beam model for dynamic instability of single-walled carbon nanotubes. Applied Mathematics and Mechanics (English Edition), 37(2), 265–274 (2016) https://doi.org/10.1007/s10483-016-2030-8

    Article  MathSciNet  Google Scholar 

  26. TANG, M., NI, Q., WANG, L., LUO, Y. Y., and WANG, Y. K. Nonlinear modeling and size-dependent vibration analysis of curved microtubes conveying fluid based on modified couple stress theory. International Journal of Engineering Science, 84, 1–10 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  27. TANG, Y. and YANG, T. Z. Post-buckling behavior and nonlinear vibration analysis of a fluid-conveying pipe composed of functionally graded material. Composite Structures, 185, 393–400 (2018)

    Article  Google Scholar 

  28. FAROKHI, H., GHAYESH, M. H., GHOLIPOUR, A., and HUSSAIN, S. Modal interactions and energy transfers in large-amplitude vibrations of functionally graded microcantilevers. Journal of Vibration and Control, 24, 3882–3893 (2017)

    Article  MathSciNet  Google Scholar 

  29. TANG, Y. and YANG, T. Z. Bi-directional functionally graded nanotubes: Fluid conveying dynamics. International Journal of Applied Mechanics, 10, 1850041 (2018)

    Article  Google Scholar 

  30. WANG, L., DAI, H. L., and NI, Q. Mode exchange and unstable modes in the dynamics of conical pipes conveying fluid. Journal of Vibration and Control, 22, 1003–1009 (2014)

    Article  MathSciNet  Google Scholar 

  31. YU, D. L., PAÏDOUSSIS, M. P., SHEN, H. J., and WANG, L. Dynamic stability of periodic pipes conveying fluid. Journal of Applied Mechanics, 81, 011008 (2014)

    Article  Google Scholar 

  32. RAJAVEL, B. and PRASAD, M. G. Acoustics of corrugated pipes: a review. Applied Mechanics Reviews, 65, 05Ï (2013)

    Article  Google Scholar 

  33. HARTNETT, J. P., IRVINE, T. F., GREENE, G. A., and CHO, Y. I. Advances in Heat Transfer, Academic Press, 187–228 (1998)

    Google Scholar 

  34. SHU, C. Differential Quadrature and Its Application in Engineering, Springer, London (2000)

    Book  MATH  Google Scholar 

  35. WANG, L. and NI, Q. The nonlinear dynamic vibrations of a restrained pipe conveying fluid by differential quadrature method (in Chinese). Journal of Dynamics and Control, 2, 58–63 (2004)

    Google Scholar 

  36. WANG, L. and NI, Q. Nonlinear dynamics of a fluid-conveying curved pipe subjected to motion-limiting constraints and a harmonic excitation. Journal of Fluids and Structures, 24, 96–110 (2008)

    Article  Google Scholar 

  37. NI, Q., TANG, M., WANG, Y. K., and WANG, L. In-plane and out-of-plane dynamics of a curved pipe conveying pulsating fluid. Nonlinear Dynamics, 75, 603–619 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  38. ZHAO, Q. L. and SUN, Z. L. In-plane forced vibration of curved pipe conveying fluid by Green function method. Applied Mathematics and Mechanics (English Edition), 38(10), 1397–1414 (2017) https://doi.org/10.1007/s10483-017-2246-6

    Article  MathSciNet  MATH  Google Scholar 

  39. DAI, H. L., WANG, L., QIAN, Q., and GAN, J. Vibration analysis of three-dimensional pipes conveying fluid with consideration of steady combined force by transfer matrix method. Applied Mathematics and Computation, 219, 2453–2464 (2012)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Tianjin Key Laboratory of Nonlinear Dynamics and Control, Department of Mechanics, School of Mechanical Engineering, Tianjin University, Tianjin, 300072, China

    Yingjie Wang, Qichang Zhang, Wei Wang & Tianzhi Yang

Authors
  1. Yingjie Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qichang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Tianzhi Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Wang.

Additional information

Citation: WANG, Y. J., ZHANG, Q. C., WANG, W., and YANG, T. Z. In-plane dynamics of a fluid-conveying corrugated pipe supported at both ends. Applied Mathematics and Mechanics (English Edition) 40(8), 1119–1134 (2019) https://doi.org/10.1007/s10483-019-2511-6

Project supported by the National Natural Science Foundation of China (Nos. 11872044, 11702192, and 11672187) and the National Key Research and Development Program of China (No. 2018YFB0106200)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Y., Zhang, Q., Wang, W. et al. In-plane dynamics of a fluid-conveying corrugated pipe supported at both ends. Appl. Math. Mech.-Engl. Ed. 40, 1119–1134 (2019). https://doi.org/10.1007/s10483-019-2511-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-019-2511-6

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation