1 Introduction

Identification of structural damages and loads are crucial problems in structural health monitoring (SHM), since accurate knowledge of external loads and damages is important for maintaining safety and integrity of monitored structures. Especially, identification of moving loads or masses is important not only for assessment of pavements or bridges but also in traffic studies, in design code calibration, for traffic control, etc. Several techniques have been developed, which address both these identification problems separately: either they identify the damage while assuming load characteristics to be known or they identify the moving load, but the structure is assumed to be undamaged. However, although in real applications unknown damages and unknown moving loads can coexist and together influence the response of the system, it seems that their simultaneous identification is a relatively unexplored area.

Damage identification is the primary task of most of structural health monitoring (SHM) systems. In general, all existing methods can be divided into two groups: local and global approaches. Local monitoring methods locate and identify small defects in narrow inspection zones via ultrasonic testing (Staszewski 2003; Ostachowicz et al. 2009) or statistical classification techniques (Silva et al. 2008; Nair et al. 2006). These methods do not require structural modeling and are outside the scope of this paper. Global methods are used for identification of significant defects in large inspection zones that are usually the whole monitored structures. In Kołakowski et al. (2006), the global methods are further categorized as pattern-recognition and model-based; the latter utilize deterministic model-updating methods (Mottershead and Friswell 1993) and are often coupled with quick reanalysis techniques (Kołakowski et al. 2008). The identification problem is often analyzed in the frequency domain and solved using modal methods, which detect, locate and identify damages via respective changes of the related modal parameters; a comprehensive summary review can be found in Doebling et al. (1998). In recent years, the wavelet analysis has become a popular tool (Peng and Chu 2004; Kim and Melhem 2004); it is often used together with pattern-recognition methods (Mujica et al. 2008). For non-stationary and moving loads, the analysis is most often performed in the time domain via a direct comparison of the simulated and measured responses. Majumder and Manohar (2003, 2004) propose a method for damage identification of linear and non-linear beams excited by a moving oscillator; the beam and the oscillator are treated together as a single coupled and time-varying system. Sieniawska et al. (2009) use a static substitute of the equation of motion for identification of parameters of a linear structure from its responses to a moving load of a known constant magnitude.

Identification of moving loads has been studied extensively in the past two decades (Yu and Chan 2007). Direct measurements of the dynamic axle loads of vehicles is expensive, difficult and subject to bias. Therefore, techniques of indirect identification from measured responses have been studied, as they can be performed easier and at lower costs. Chan, Law et al. have proposed four general methods for indirect identification, which are the time-domain method (TDM) (Law et al. 1997), the frequency-time domain method (FTDM) (Law et al. 1999), Interpretive Method I (IMI) (Chan and O’Connor 1990) and Interpretive Method II (IMII) (Chan et al. 1999). All of them require the parameters of the model of the bridge to be known in advance. Each method has its merits and limitations, which are compared in Chan et al. (2001). The numerical ill-conditioning of the problem seems to be the main factor that decreases the accuracy of the identification results. To improve the accuracy, techniques based on the singular value decomposition (SVD) have been investigated and adopted for the inverse computation (Yu and Chan 2003). Other regularization methods have been also used, e.g. Law et al. (2001) and Zhu and Law (2006) use the Tikhonov regularization, while Law and Fang (2001) and González et al. (2008) couple it with the dynamic programming approach. However, finding the optimal value of the regularization parameter is numerically costly and requires long computational time. Moreover, the regularization parameter turns out to be sensitive to the properties of the vehicle and the bridge and hard to be precisely assigned; see Pinkaew (2006) and Pinkaew and Asnachinda (2007), where a method called the updated static component (USC) technique is proposed, which extracts the static component of the load and identifies iteratively only the dynamic component in order to decrease the sensitivity of the regularization parameter. The existing techniques are often based on modal decomposition and can suffer from the truncation error. As discussed in Law et al. (2004) and Zhu and Law (2002), identification techniques based on the finite element method can avoid the modal truncation error and allow the identification to be applied to structures of a more complex geometry in comparison with the methods based on the continuous system description. In general, all these methods require a known and well-defined model of the structure in order to build the load–response relation, even if some of them allow for the identification of chosen additional parameters besides the moving load, such as the prestressing force (Law et al. 2008) or parameters of the vehicle model (Jiang et al. 2004). The moving forces are usually treated as the unknown variables instead of the masses; in this way, the identification problem is linearized, but at the cost of increased ill-conditioning and a larger number of sensors. The number of the sensors must be then equal or exceed the number of the moving forces in order to obtain a unique solution, while the resulting ill-conditioning makes regularization techniques necessary to obtain meaningful solutions.

In the case of unknown excitations and unknown structural damages, the related identification problems are inherently coupled: both factors together influence the structural response and cannot be identified independently from each other. Hoshiya and Maruyama (1987) apply a weighted global iteration procedure and the extended Kalman filter for simultaneous identification of a moving force and modal parameters of a simply supported beam. Lu and Law (2007) identify damage and parameters of a non-moving impulsive or sinusoidal force excitations in a two-step identification process using a limited number of measurements. Zhang et al. (2009a) present a method for simultaneous identification of structural physical parameters and an unknown support excitation. However, in the case of an unknown moving load, the coupled vehicle–bridge system is a time-varying system with characteristics that can be significantly different from those of the bridge alone (Kim et al. 2003). As a result, the interaction between the bridge and the vehicle has to be accounted for in the identification process. Zhu and Law (2007) propose a method for simultaneous identification of moving loads and damages using a two-step approach that separately adjusts the loads and the damage factors in each iteration of the optimization process; the number of sensors is one less than the number of the beam elements.

An earlier paper by the authors (Zhang et al. 2010) addressed simultaneous identification of damages and non-moving excitation forces in truss structures; a moving force could be identified only by a simultaneous identification of all load-time histories in all involved degrees of freedom (DOFs). Here, simultaneous identification is addressed in the case of moving loading masses. Both papers use the virtual distortion method (VDM, Holnicki-Szulc and Gierliński 1995) to model the structural damages. The formulation of the current paper is no longer restricted to truss structures and addresses also modeling of the time-varying coupled system of moving masses and the supporting structure. In the research on moving load identification, the moving forces are usually treated as the unknown variables. Similarly, in the above-mentioned earlier paper, the unknown damages were characterized in terms of the time histories of the virtual distortions. As a result, no damage model was necessary: the damages of unknown types could be identified via an analysis of the computed strain-stress relationships of the damaged elements. Here, in contrast, the damage extents and the moving masses are used as the unknowns. This choice yields a far smaller number of optimization variables, dramatically improves the conditioning of the identification process and decreases the number of sensors that are required for a unique solution. Damage is modeled in terms of stiffness reduction of the damaged elements, which seems to be typical for global methods of structural health monitoring (Dems and Mróz 2001). Given the identified masses, the corresponding moving loads can be computed straightforwardly, since the forces and the distortions are related to the optimization variables via a simple linear system. In this way, the optimization variables related to the masses and to the damages are treated in a unified way, so that all standard optimization algorithms can be directly used. The numerical costs are considerably reduced by using the concept of the moving dynamic influence matrix, which is defined as a collection of the structural impulse–responses with respect to the time-dependent positions of the moving masses. For given values of the variables, the moving dynamic influence matrix allows the response of the system to be computed quickly without a full numerical simulation and a repetitive assembly of the time-variant mass matrix in each time step. A fast sensitivity analysis is proposed based on the adjoint variable method. This paper is a completely rewritten and substantially extended version a paper presented at the WCSMO-8 (Zhang et al. 2009b). The material extensions include the exact continuous-time formulation, which is no longer limited to frame structures, and the sensitivity analysis.

The three following sections describe the direct problems of, respectively, modeling of damage via the virtual distortions, modeling of moving masses using the dynamic influence matrix and the coupled modeling of moving masses and damage. The fifth section discusses the inverse identification problem. The sixth section tests the approach in a numerical example using a three-span frame structure, simulated measurement error at the level of 10% rms and three concurrent types of model errors. The approach and the results are discussed in the seventh section.

2 Modeling of damage

For modeling of damage the Virtual Distortion Method (VDM) is used, which is a quick reanalysis method applicable for static and dynamic analysis of structures (Kołakowski et al. 2008; Holnicki-Szulc and Gierliński 1995). Structural modifications, including damages, and physical nonlinearities like material yielding, are modeled in terms of the related response-coupled virtual distortions, which are additional strains imposed on the involved elements of the original structure (equivalent to certain locally applied pseudo-loads).

The damaged structure is thus modeled by the original undamaged structure subjected to the virtual distortions (distorted structure). The virtual distortions are related to the damage parameters by the requirement that both structures are equivalent in the terms of element forces, which yields a system of linear integral equations with the virtual distortions as the unknowns, (20). As the original structure is assumed to be linear, the response of the distorted structure to an external excitation can be expressed as the sum of the responses of the original undamaged structure to (a) the same excitation and to (b) the virtual distortions, (18). In this way, the response of the distorted/damaged structure is expressed solely in the terms of certain characteristics of the original undamaged structure, which eliminates the need for repeated updating and simulations of the finite element (FE) model.

For the sake of notational simplicity, reduction of element stiffness is the only damage type considered here. However, the methodology can be straightforwardly extended to include other damage patterns like breathing cracks (Zhang et al. 2010) and mass-related modifications as well as plastic yielding of the structural elements (Holnicki-Szulc 2008; Kołakowski et al. 2008; Jankowski 2009), provided the assumption of small deformations is satisfied.

2.1 Equation of motion and global pseudo-load

The basic relations between damage extent, pseudo-loads, virtual distortions and the response of the damaged structure can be deduced in general terms of the FE method. Let the damage extent of the ith finite element be quantified by the proportion ratio μ i between its original stiffness matrix K i and the modified stiffness matrix \(\tilde{\mathbf{K}}_i\),

$$ \label{eq:damageExtent} \tilde{\mathbf{K}}_i = \mu_i \mathbf{K}_i, $$
(1)

where K i and \(\tilde{\mathbf{K}}_i\) are expressed in global DOFs. The stiffness matrix of the entire damaged structure can be expressed as

$$ \tilde{\mathbf{K}} = \sum\limits_i \mu_i\mathbf{K}_i. $$
(2)

The equation of motion of the damaged structure subjected to an external excitation f(t),

$$ \label{eq:dmon} \mathbf{M}\ddot{\bf{u}}(t) + \mathbf{C}\dot{\mathbf{u}}(t) + \tilde{\mathbf{K}}{\bf u}(t) = \mathbf{f}(t), $$
(3)

where u(t) denotes the displacement response of the structure, can be therefore transformed into the equation of motion of the distorted structure, that is the original undamaged structure subjected to the same external excitation f(t) and a certain response-coupled pseudo-load p 0(t),

$$ \label{eq:mondis} \mathbf{M}\ddot{\bf{u}}(t) + \mathbf{C}\dot{\mathbf{u}}(t) + \mathbf{Ku}(t) = \mathbf{f}(t) + \mathbf{p}^0(t), $$
(4)

where the pseudo-load p 0(t) models the damage and is related to the damage extents by

$$\label{eq:pseudoLoad} \mathbf{p}^0(t) = \sum\limits_i \left( 1-\mu_i \right) \mathbf{K}_i \mathbf{u}(t). $$
(5)

2.2 Local pseudo-loads

The stiffness matrix of the ith element, K i , is formulated in the global DOFs. It can be related to the local DOFs by

$$\label{eq:KiLocalGlobal} \mathbf{K}_i = \mathbf{L}_i^\text{T} \mathbf{T}_i^\text{T} \mathbf{K}_{\text{e},i} \mathbf{T}_i \mathbf{L}_i, $$
(6)

where \(\mathbf{K}_{\text{e},i}\) is the stiffness matrix of the ith element expressed in its local coordinates, L i is the localization matrix linking the global DOFs to the local DOFs and T i is the transformation matrix from the global to the local coordinate system. In a similar way, the vector \(\mathbf{u}_{\text{e},i}(t)\) of the nodal displacements of the ith element in its local coordinate system can be related to the global displacement vector u(t) by

$$ \label{eq:uei} \mathbf{u}_{\text{e},i}(t) = \mathbf{T}_i \mathbf{L}_i \mathbf{u}(t). $$
(7)

Equations (6) and (7) can be substituted in (5). As a result, the global pseudo-load p 0(t) is expressed in the terms of element-specific local pseudo-loads \(\mathbf{p}^0_{\text{e},i}(t)\),

$$ \label{eq:p} \mathbf{p}^0(t) = \sum\limits_i \mathbf{L}_i^\text{T} \mathbf{T}_i^\text{T} \mathbf{p}^0_{\text{e},i}(t), $$
(8)

where \(\mathbf{p}^0_{\text{e},i}(t)\) is expressed in the local DOFs as

$$ \label{eq:p0} \mathbf{p}^0_{\text{e},i}(t) = (1-\mu_i) \mathbf{K}_{\text{e},i} \mathbf{u}_{\text{e},i}(t). $$
(9)

Since the term \(\mathbf{K}_{\text{e},i} \mathbf{u}_{\text{e},i}{(t)}\) represents the local nodal loads \(\mathbf{p}_{\text{e},i}{(t)}\), there is a straightforward relation between the local nodal loads and the local pseudo-loads:

$$ \label{eq:p0mup} \mathbf{p}^0_{\text{e},i}{(t)} = \left( 1-\mu_i \right) \mathbf{p}_{\text{e},i}{(t)}. $$
(10)

Note that (10) is an implicit equation, since the pseudo-load is coupled with the response, that is the nodal loads \(\mathbf{p}_{\text{e},i}{(t)}\) on the right-hand side depend on the load \(\mathbf{p}^0_{\text{e},i}{(t)}\).

2.3 Virtual distortions

For a truss structure with simple one-dimensional elements, the pseudo-load that models the damage of an element is a pair of self-equilibrated axial forces applied at its nodes; it corresponds to a single axial distortion state. In elements of other types, more distortion states can occur. For each element, their number and shapes can be analyzed via the eigenvalue problem of the local stiffness matrix \(\mathbf{K}_{\text{e},i}\). The matrix is positive semi-definite, hence its eigenvectors are of two kinds only: rigid motion vectors that correspond to zero eigenvalues and distortion vectors that correspond to positive eigenvalues. The matrix \(\mathbf{K}_{\text{e},i}\) can be expressed in the terms of its positive eigenvalues λ ij and the corresponding distortion vectors φ ij as

$$\label{eq:K} \mathbf{K}_{\text{e},i} = \sum\limits_j \lambda_{ij}\, \boldmath{\varphi}_{ij}\, \boldmath{\varphi}_{ij}^\text{T}. $$
(11)

The eigenvector φ ij represents the jth local unit distortion. The corresponding vector of the nodal loads is

$$\label{eq:eigen} \mathbf{K}_{\text{e},i} \boldmath{\varphi}_{ij} = \lambda_{ij} \boldmath{\varphi}_{ij}. $$
(12)

Using (9), (11) and (12), the local pseudo-load can be expressed in terms of a combination of the local virtual distortions,

$$\label{eq:pb} \mathbf{p}_{\text{e},i}^0{(t)} = \mathbf{K}_{\text{e},i} \sum\limits_j \kappa_{ij}^0{(t)} \boldmath{\varphi}_{ij}, $$
(13)

where \(\kappa_{ij}^0{(t)} \boldmath{\varphi}_{ij}\) is the jth virtual distortion of the ith element and

$$ \kappa_{ij}^0{(t)} = \left( 1-\mu_i \right) \boldmath{\varphi}_{ij}^\text{T} \mathbf{u}_{\text{e},i}{(t)} $$
(14)

is the combination coefficient of the corresponding jth local unit distortion φ ij . The local nodal loads can be expressed in similar terms as

$$ \mathbf{p}_{\text{e},i}{(t)} = \mathbf{K}_{\text{e},i} \sum\limits_j \kappa_{ij}{(t)} \boldmath{\varphi}_{ij}, $$
(15)

where the combination coefficient is given by

$$ \label{eq:distortion} \kappa_{ij}{(t)} = \boldmath{\varphi}_{ij}^\text{T} \mathbf{u}_{\text{e},i}{(t)}. $$
(16)

Therefore, a relation similar to (10) is yielded:

$$\label{eq:r} \kappa_{ij}^0{(t)} = \left( 1-\mu_i \right) \kappa_{ij}{(t)}. $$
(17)

For a 2D beam element, the local stiffness matrix has three positive eigenvalues and three corresponding distortion vectors. Apart from the pure axial distortion (the same as in a truss element), there occur also a pure bending and a bending/shear distortion (Świercz et al. 2008), see Fig. 1.

Fig. 1
figure 1

Three distortion states of a beam element

Full size image

2.4 The response

With the assumption of zero initial conditions, the response y α (t) of the αth sensor (linear sensor of any type, e.g. strain sensor, accelerometer, etc.), in an externally excited damaged structure is modeled by the VDM as the following sum of the linear and the residual parts

$$ \label{eq:res} y_\alpha (t) = y_\alpha^\text{L}(t) + \sum\limits_{i,j} \int_0^t D_{\alpha i j}^\kappa (t-\tau) \kappa^0_{ij}(\tau) \,d\tau, $$
(18)

where \(y_\alpha^\text{L}(t)\) denotes the response of the original undamaged structure to the same external excitation, and \(\kappa^0_{ij} (t)\) describes the jth virtual distortion of the ith element. The function \(D^\kappa_{\alpha i j}(t)\) denotes the impulse–response of the original undamaged structure, and in the scope of the VDM it is called the dynamic influence matrix; it is the response of the αth sensor to an impulse unit distortion φ ij of the ith element. Such an impulse distortion is the excitation that is equivalent to a local impulsive load \(\mathbf{K}_{\text{e},i} \varphi_{ij}\). In case y α (t) is acceleration, the impulse–response may contain an impulsive component at t = 0. The formulation requires the assumption of small deformations, so that the responses can be linearly combined.

Equation (18) can be used to compute the response y α (t), provided the virtual distortions \(\kappa^0_{ij} (t)\) are known. In order to compute them, the distortion response κ ij (t) of the damaged structure, (16), is expressed in a similar way to (18),

$$ \label{eq:resDistortion} {\kappa_{ij} (t) = \kappa_{ij}^\text{L}(t) + \sum\limits_{k,l} \int_0^t D_{ijkl}^{\kappa\kappa} (t-\tau) \kappa^0_{kl}(\tau) \,d\tau,} $$
(19)

where \(D_{ijkl}^{\kappa\kappa} (t)\) is the corresponding impulse–response function (dynamic influence matrix) of the original undamaged structure. Equation (19), if substituted in (17), yields the following integral equation:

$$\begin{array}{lll} \label{eq:volterraDamage} (1 - \mu_i) \kappa_{ij}^\text{L}(t) &= \kappa^0_{ij} (t) - (1 - \mu_i) \\ &{\kern10pt} \times\,\sum\limits_{k,l} \int_0^t D_{ijkl}^{\kappa\kappa} (t-\tau) \kappa^0_{kl}(\tau) \,d\tau \end{array} $$
(20)

that, if collected for all damaged elements i and distortions j, is a system of Volterra integral equations of the second kind, which is always well-posed and thus uniquely solvable (Kress 1989).

3 Modeling of moving masses

Moving masses in a bridge–vehicle system not only excite the supporting structure via their gravities but also modify its inertial properties. Here, similar as in the case of structural damages, moving masses are modeled via the corresponding moving pseudo-loads that include their gravities and the inertial effects. The structural response can be quickly computed via the convolution of the pseudo-loads with the pre-computed structural impulse–response; in this way, repeated numerical integration of the equation of motion as well as updating the mass matrix in each time step are both avoided.

3.1 Pseudo-loads

Consider n m masses \(m_1,\ldots,m_{n_\text{m}}\) moving at constant velocities \(v_1,\ldots,v_{n_\text{m}}\) on a flat supporting structure of length L (the undamaged bridge); Fig. 2 illustrates the considered setup using a simply supported beam in the role of the bridge. Each mass is assumed to attach to the bridge at its current position, which for the mass m i is x i  = x i,0 + v i t, where x i,0 denotes the initial position and v i denotes the velocity.

Fig. 2
figure 2

A sample supporting system and the moving masses

Full size image

The bridge is modeled as a discrete finite element structure. The moving masses and the bridge are collectively considered a single system, which is exposed to moving external loads of the constant gravities of the masses; the global excitation vector is computed in each time step using the shape functions of the finite elements that currently carry the masses. The system mass matrix is continuously re-assembled with respect to the current positions of the masses. The equation of motion of the system can be thus written as

$$\begin{array}{lll} \label{eq:motion} &\left[ \mathbf{M} + \Delta \mathbf{M}(t) \right] \ddot{\mathbf{u}}^\text{L}(t) + \mathbf{C}\dot{\mathbf{u}}^\text{L}(t) + \mathbf{K}\mathbf{u}^\text{L}(t)\\ &{\kern8pt} = \sum\limits_{i=1}^{n_\text{m}} m_i g\, \mathbf{b}_i(t), \end{array} $$
(21)

where M, C and K are the mass, damping and stiffness matrices of the undamaged bridge. The matrix ΔM(t) models the effects of the attached masses,

$$ \Delta \mathbf{M}(t) = \sum_{i=1}^{n_\text{m}} m_i \mathbf{b}_i (t) \mathbf{b}_i^\text{T} (t), $$
(22)

and b i (t) denotes the time-dependent global load allocation vector of the ith mass. The vector b i (t) vanishes if the mass is outside the bridge; otherwise, it is computed using the shape functions of the finite element that currently carries the mass. The dynamic response of the bridge can be obtained by a numerical integration of (21), provided the velocities of the masses are well below the critical speed (Bajer and Dyniewicz 2009).

In accordance with the general idea of the VDM, the time-dependent matrix ΔM(t) in (21) is moved to the right-hand side to obtain:

$$ \label{eq:motionbr} {\mathbf{M} \ddot{\mathbf{u}}^\text{L}(t) + \mathbf{C}\dot{\mathbf{u}}^\text{L}(t) + \mathbf{Ku}^\text{L}(t) = \sum\limits_{i=1}^{n_\text{m}} p_i(t) \mathbf{b}_i(t),} $$
(23)

which is the equation of motion of the bridge alone subjected to the moving pseudo-loads p i (t) that act at the positions of the moving masses and represent both their gravities and the inertial effects:

$$ \label{eq:pseudoMoving} p_i(t) = m_i \left[g-a_i(t)\right], $$
(24)

where the vertical acceleration of the ith mass a i (t) couples the pseudo-load p i (t) back to the structural response,

$$ \label{eq:vertAccelMoving} { a_i(t) = \mathbf{b}_i^\text{T}(t)\ddot{\mathbf{u}}^\text{L}(t). } $$
(25)

3.2 Moving dynamic influence matrix

The dependence of the vertical accelerations of the moving masses on the pseudo-loads p i (t) can be expressed explicitly by using in (25) the impulse–response matrix \(\ddot{\mathbf{H}}(t)\) that describes acceleration responses of the bridge to unit impulse excitations:

$$\begin{array}{lll} \label{eq:Dna} a_i (t) &= \mathbf{b}_i^\text{T}(t) \int_0^t \ddot{\mathbf{H}} (t-\tau) \sum\limits_{j=1}^{n_\text{m}} p_j(\tau) \mathbf{b}_j(\tau) \,d\tau\\ &= \sum\limits_{j=1}^{n_\text{m}} \int_0^t D^\text{mm}_{ij}(t,\tau) p_j(\tau) \,d\tau, \end{array} $$
(26)

where the convolution kernel \(D^\text{mm}_{ij}(t,\tau)\) represents the vertical acceleration of the ith mass at time t as a result of an impulsive excitation applied at time τ at the respective location of the jth mass,

$$ \label{eq:movingInflMatrix} D^\text{mm}_{ij}(t,\tau) = \mathbf{b}^\text{T}_i(t) \ddot{\mathbf{H}}(t-\tau) \mathbf{b}_j(\tau). $$
(27)

Equation (26) can be substituted in (24), which can be then stated in the following standard form:

$$ \label{eq:DnaVolterra} m_i g = p_i (t) + m_i \sum\limits_{j=1}^{n_\text{m}} \int_0^t D^\text{mm}_{ij}(t,\tau) p_j(\tau) \,d\tau $$
(28)

that, if collected for all moving masses, constitutes a system of linear integral equations with the pseudo-loads p i (t) as the unknowns, which is analogical to (20). The kernel of the respective matrix integral operator, \(D_{ij}^\text{mm}(t,\tau)\), is expressed with respect to the changing positions of the moving masses and thus ceases to be a difference kernel; notice that an impulsive component occurs on its diagonal. The kernel, or its discrete version (Section 4.3), is the proposed in this paper moving dynamic influence matrix. As it does not depend on the masses, it needs to be computed only once for a certain bridge and given velocities of the masses. Thereupon, in the coupled bridge–moving mass analysis, the pseudo-loads p i (t) that model the masses can be quickly found by solving (a discrete version of) (28). In this way, it is possible to avoid the repeated assembling of the system mass matrix in each time step, as required by (21). As described in the following sections, this is an important advantage in moving mass identification.

3.3 The response

Given the pseudo-loads p i (t) and zero initial conditions, the response y α (t) of the αth linear sensor placed in the structure that is excited by the considered moving masses is modeled, as in (18) and (26), in the following way:

$$ \label{eq:resMoving} { y^\text{L}_\alpha (t) = \sum\limits_{i=1}^{n_\text{m}} \int_0^t D_{\alpha i}^\text{m} (t,\tau) p_i(\tau) \,d\tau, } $$
(29)

where \(D_{\alpha i}^\text{m} (t,\tau)\) denotes the impulse–response of the structure, that is the response of the αth sensor at time t to the unit impulsive excitation at time τ at the respective location of the ith mass, which, in case \(y^\text{L}_\alpha(t)\) is acceleration, may contain an impulsive component.

4 Coupled modeling of moving masses and damage

4.1 Virtual distortions and pseudo-loads

As shown in the preceding sections, damage and moving masses can be separately modeled using virtual distortions and pseudo-loads. Since these are both coupled to the response, in case of a damaged structure excited by moving masses they influence each other and cannot be used independently. In such a case, a coupled analysis is necessary. First, the distortion and the acceleration responses of the structure are stated in the following form:

$$\begin{array}{lll} a_i (t) &= \sum\limits_{j=1}^{n_\text{m}} \int_0^t D^\text{mm}_{ij}(t,\tau) p_j(\tau) \,d\tau \\ &\quad + \sum\limits_{j,k} \int_0^t D_{ijk}^{\text{m}\kappa} (t,\tau) \kappa^0_{jk}(\tau) \,d\tau, \label{eq:DnaBoth}\\ \end{array} $$
(30)
$$\begin{array}{lll} \kappa_{ij} (t) &= \sum\limits_{k=1}^{n_\text{m}} \int_0^t D^{\kappa\text{m}}_{ijk}(t,\tau) p_k(\tau) \,d\tau \\ &\quad + \sum\limits_{k,l} \int_0^t D_{ijkl}^{\kappa\kappa} (t-\tau) \kappa^0_{kl}(\tau) \,d\tau, \label{eq:resDistortionBoth} \end{array} $$
(31)

which is similar to (19) and (26) but takes account of the mutual dependence of the distortions and accelerations, which is expressed via the respective impulse–responses (dynamic influence matrices): \(D_{ijk}^{\text{m}\kappa} (t,\tau)\), which is the vertical acceleration of the ith mass at time t to an impulse unit distortion φ jk of the jth element applied at time τ, and \(D^{\kappa\text{m}}_{ijk}(t,\tau)\), which is the jth distortion of the ith element at time t as a result of an impulse excitation applied at time τ at the respective location of the kth mass. Using (17) and (24), the following system of linear integral equations is yielded:

$$\begin{array}{lll} m_i g &= p_i (t) + m_i \sum\limits_{j=1}^{n_\text{m}} \int_0^t D^\text{mm}_{ij}(t,\tau) p_j(\tau) \,d\tau \\ &\quad + m_i \sum\limits_{j,k} \int_0^t D_{ijk}^{\text{m}\kappa} (t,\tau) \kappa^0_{jk}(\tau) \,d\tau,\label{eq:volterraBoth1} \end{array} $$
(32)
$$\begin{array}{lll} 0 &= (1 - \mu_i) \sum\limits_{k=1}^{n_\text{m}} \int_0^t D^{\kappa\text{m}}_{ijk}(t,\tau) p_k(\tau) \,d\tau - \kappa^0_{ij}(t)\\ &\quad + (1 - \mu_i) \sum\limits_{k,l} \int_0^t D_{ijkl}^{\kappa\kappa} (t-\tau) \kappa^0_{kl}(\tau) \,d\tau,\label{eq:volterraBoth2} \end{array} $$
(33)

with the pseudo-loads p i (t) and the virtual distortions \(\kappa^0_{ij}(t)\) as the unknowns. Notice that the masses m i and the damage extents μ i , which are to be identified, occur in the kernel of the respective matrix integral operator only in the form of constant scaling factors, so that for a given structure the kernel has to be computed only once and does not have to be recomputed during the identification process.

4.2 Response of a damaged structure to moving masses

By solving (32) and (33), the pseudo-loads and the virtual distortions are obtained. The response of the αth sensor can be then computed as follows, see (18) and (29),

$$\begin{array}{lll} \label{eq:resBoth} y_\alpha (t) &= \sum\limits_{i=1}^{n_\text{m}} \int_0^t D_{\alpha i}^\text{m} (t,\tau) p_i(\tau) \,d\tau \\ &\quad + \sum\limits_{i,j} \int_0^t D_{\alpha i j}^\kappa (t-\tau) \kappa^0_{ij}(\tau) \,d\tau. \end{array} $$
(34)

4.3 Discretization

In applications, the responses are usually either measured or obtained through numerical simulations and thus discrete. Therefore, in practice only the discrete counterparts of (30) to (34) are used. The discrete response of the damaged structure subjected to moving loads is then expressed as

$$ \label{eq:resBothDiscrete} \mathbf{y} = \mathbf{D}^\text{m} \mathbf{p} + \mathbf{D}^\kappa \boldmath{\kappa}^0, $$
(35)

where the vectors y, κ 0 and p collect, for all time steps, the discrete responses (of all considered sensors), the discrete virtual distortions (of all potentially damaged elements) and the pseudo-loads; thus, they are respectively of lengths \(n_\text{a}n_\text{t}\), \(n_\text{d}n_\text{t}\) and \(n_\text{m}n_\text{t}\), where \(n_\text{t}\) is the number of the time steps, \(n_\text{a}\) is the number of the sensors, \(n_\text{d}\) is the total number of the considered virtual distortions and \(n_\text{m}\) is the number of the moving masses. The matrices \(\mathbf{D}^\text{m}\) and D κ are the discrete counterparts of the corresponding integral operators in (34) and take the forms of block matrices of respective dimensions with lower-triangular \(n_\text{t}\times n_\text{t}\) blocks, which in case of D κ are Toeplitz, as the corresponding operator has a difference kernel. Similarly, the discrete accelerations a and the discrete distortions κ depend on the discrete pseudo-load p and the discrete virtual distortions κ 0 in the following way:

$$ \label{eq:BothDiscrete} \left[\!\begin{array}{c} \mathbf{a} \\ \boldmath{\kappa} \end{array}\!\right] = \left[\!\begin{array}{ll} \mathbf{D}^\text{mm} & \mathbf{D}^{\text{m}\kappa}\\ \mathbf{D}^{\kappa\text{m}} & \mathbf{D}^{\kappa\kappa} \end{array}\!\right] \left[\!\begin{array}{c} \mathbf{p} \\ \boldmath{\kappa}^0 \end{array}\!\right], $$
(36)

which is an aggregated discrete version of (30) and (31). Finally, the integral equations (32) and (33), if similarly discretized, become the following large linear system

$$ \label{eq:volterraBothDiscrete} \left[\!\!\begin{array}{cc} \mathbf{I}+\mathbf{m}\mathbf{D}^\text{mm} & \mathbf{m}\mathbf{D}^{\text{m}\kappa} \\ (\mathbf{I}-\boldmath{\mu})\mathbf{D}^{\kappa\text{m}} & (\mathbf{I}-\boldmath{\mu})\mathbf{D}^{\kappa\kappa} - \mathbf{I} \end{array}\!\!\right] \left[\!\!\begin{array}{c} \mathbf{p} \\ \boldmath{\kappa}^0 \end{array}\!\!\right] = \left[\!\!\begin{array}{c} \mathbf{mg} \\ \mathbf{0} \end{array}\!\!\right], $$
(37)

where m and μ are block diagonal matrices of respective dimensions with diagonal blocks \(m_i\,\mathbf{I}_{n_\text{t}\times n_\text{t}}\) and \(\mu_i\,\mathbf{I}_{n_\text{t}\times n_\text{t}}\), and g is the vector of appropriate length of Earth’s gravities g. Equation (37) can be also deduced directly from (36), given the following aggregated versions of (17) and (24):

$$\mathbf{p}\, = \mathbf{m} \left(\mathbf{g}-\mathbf{a}\right), \label{eq:rDiscrete}\\ $$
(38)
$$\boldmath{\kappa}^0 = \left( \mathbf{I}-\boldmath{\mu} \right) \boldmath{\kappa}. \label{eq:pseudoMovingDiscrete} $$
(39)

The building blocks of (35) to (37) are the matrices D (·) and D (·)(·). These matrices store all the necessary information about the dynamics of the structure and are independent of the moving masses and the damage. Thus, given specific values of the masses m i and the damage extents μ i , the system (37) can be quickly assembled without any numerical simulations and then solved to obtain the pseudo-loads and the virtual distortions, which can be then used in (35) to compute the response of the damaged structure excited by the moving masses.

5 Identification

Given the measured response \(\mathbf{y}^\text{M}\) of the damaged structure to unknown moving masses, there are two general approaches to identify the unknown damage and the masses. The first approach treats the pseudo-load p and the virtual distortions κ 0 as independent unknowns. The following version of (35),

$$ \label{eq:resBothDiscreteM} \mathbf{y}^\text{M} = \mathbf{D}^\text{m} \mathbf{p} + \mathbf{D}^\kappa \boldmath{\kappa}^0, $$
(40)

is solved with respect to the unknown p and κ 0, which are then used in (36) in order to compute the corresponding accelerations a and distortions κ. Finally, the unknown masses and damages are estimated via least-square fitting of (38) and (39). An advantage of the approach is the linearity of the problem of solving (40). Moreover, the virtual distortions of a damaged element are all treated as independent from each other and in all time steps, hence exactly the same approach can be used to identify stiffness-related damages of unknown types (not only a simple stiffness reduction), as demonstrated in Zhang et al. (2010) using a truss structure. However, the problem of solving (40) is a well-known ill-conditioned problem (Hansen 2002), and thus extremely sensitive to measurement errors. Moreover, since all the elements of the vectors p and κ 0 are treated as independent unknowns, the number of the sensors has to be equal or greater than the total number of the unknown moving masses and the considered virtual distortions, so that the location of the damage has to be known a priori.

Therefore, this paper pursues a more practical parametric approach that treats the masses m i and the damage extents μ i as independent unknowns, which are used to determine the pseudo-load p, the virtual distortions κ 0 and finally the response y. In this way, the number of unknowns is significantly reduced and thus fewer sensors are necessary and the results are more stable; however, it is at the cost of assuming the damages to be of known types, such as the constant stiffness reduction that is considered in this paper.

5.1 Objective function and the optimization variables

Basically, the inverse problem of identification of unknown masses and damage extents is stated here as an optimization problem of minimization of the normalized mean-square distance between the measured structural response \(\mathbf{y}^\text{M}\) and the computed response y, where the optimization variables are m i and μ i . However, these variables have very different magnitudes, which can seriously impair the accuracy of many optimization procedures: the damage extents μ i belong to the interval [0,1], but the masses m i might be as large as several tens of thousands of kilograms. Moreover, while the damage extents have a natural initial value of 1 (no damage), there is no such a straightforward value for the moving masses. Thus, initial approximations of the masses (called the trial masses) are computed by assuming the bridge to be undamaged and approximating the pseudo-loads with the moving gravities of the masses, that is by solving in the least-square sense the following overdetermined system:

$$\label{eq:trial} \mathbf{y}^\text{M} = \mathbf{D}^\text{m} \mathbf{m}^\text{tr}\mathbf{g}, $$
(41)

where \(\mathbf{m}^\text{tr}\) is the diagonal matrix of the same structure as m in (37) and (38), but includes the trial masses \(m_i^\text{tr}\) on the diagonal. Given the trial masses, the optimization problem can be stated in the following dimensionless variables \(\mu_i^\star\) (\(i=1,\ldots,n_\text{m}+n_\text{e}\), where \(n_\text{e}\) is the number of the potentially damaged elements):

$$\label{eq:newVariables} \mu_i^\star = \begin{cases} \dfrac{m_i}{m^\text{tr}_i} & \text{if }i=1,\ldots,n_\text{m}, \\[10pt] \mu_{i-n_\text{m}} & \text{if }i=n_\text{m}+1,\ldots,n_\text{m}+n_\text{e}, \end{cases} $$
(42)

which all have the natural initial value of 1 and are all of the same magnitude. Therefore, the proposed optimization problem is stated in the following form:

$$ \label{eq:objt} \begin{array}{lll} {\kern-1pt} \text{minimize}\quad & f(\mu_1^\star, \ldots, \mu_{n_\text{m}+n_\text{e}}^\star) = \frac{1}{2}\frac{\Vert \mathbf{y}^\text{M} - \mathbf{y} \Vert^2} {\Vert \mathbf{y}^\text{M} \Vert^2},\\ {\kern-1pt} \text{subject to}\quad & \mu_i^\star \geq 0,\ i=1,\ldots,n_\text{m}+n_\text{e}, \end{array} $$
(43)

where y is the response computed for the assumed values of the optimization variables via (42), (37) and (35).

5.2 Sensitivity analysis

The identification process amounts to the minimization of the objective function given in (43) and can be quickly performed using gradient-based optimization algorithms, provided the gradient can be computed at a reasonable cost. The formulation based on (37) and (35) allows the discrete adjoint method to be used (Haftka and Gürdal 1992), which is quicker by one order of magnitude in comparison to the standard direct differentiation method (Papadimitriou and Giannakoglou 2008).

For notational simplicity, (35) and (37) and their first derivatives with respect to the variable \(\mu_i^\star\) are stated in the following simple aggregate forms:

$$\mathbf{Ax} = \mathbf{b}, \label{eq:volterraBothDiscreteShort}\\ $$
(44)
$$\mathbf{Ax}_i = \mathbf{b}_i-\mathbf{A}_i\mathbf{x}, \label{eq:volterraBothDiscreteShortD}\\ $$
(45)
$$\mathbf{y} = \mathbf{Dx}, \label{eq:resBothDiscreteShort}\\ $$
(46)
$$\mathbf{y}_i = \mathbf{Dx}_i, \label{eq:resBothDiscreteShortD} $$
(47)

where

$$\mathbf{A}= \left[\begin{array}{cc} \mathbf{I}+\mathbf{m}\mathbf{D}^\text{mm} & \mathbf{m}\mathbf{D}^{\text{m}\kappa} \\ (\mathbf{I}-\boldmath{\mu})\mathbf{D}^{\kappa\text{m}} & (\mathbf{I}-\boldmath{\mu})\mathbf{D}^{\kappa\kappa} - \mathbf{I} \end{array}\right], \\ $$
(48)
$$\mathbf{b} = \left[\begin{array}{cc} \mathbf{mg} & \mathbf{0} \end{array}\right]^\text{T}, \\ $$
(49)
$$\mathbf{D} = \left[\begin{array}{cc} \mathbf{D}^\text{m} & \mathbf{D}^\kappa \end{array}\right], \\ $$
(50)
$$\mathbf{x} = \left[\begin{array}{cc} \mathbf{p} & \boldmath{\kappa}^0 \end{array}\right]^\text{T}. $$
(51)

The objective function is directly differentiated to obtain

$$ \label{eq:objtD} f_i = -\frac{\left( \mathbf{y}^\text{M} - \mathbf{y} \right)^\text{T}} {\left\Vert \mathbf{y}^\text{M} \right\Vert^2} \mathbf{D} \mathbf{x}_i, $$
(52)

which includes the first derivatives x i of the optimization variables. The direct differentiation method computes it by solving (45); for the full gradient, the solution has to be repeated \(n_\text{m}+n_\text{e}\) times, that is once for each optimization variable \(\mu_i^\star\). The discrete adjoint method adds to (52) the scalar product of the adjoint vector λ with (45) and collects together the terms including x i to obtain

$$ \label{eq:objtD2} f_i = \boldmath{\lambda}^\text{T} \big( \mathbf{A}_i\mathbf{x} - \mathbf{b}_i \big) + \left( \boldmath{\lambda}^\text{T} \mathbf{A} -\frac{\left( \mathbf{y}^\text{M} - \mathbf{y} \right)^\text{T}} {\left\Vert \mathbf{y}^\text{M} \right\Vert^2}\mathbf{D} \right)\mathbf{x}_i. $$
(53)

In this way, the first derivative of the objective function is stated as

$$ \label{eq:objtD3} f_i = \boldmath{\lambda}^\text{T} \big( \mathbf{A}_i\mathbf{x} - \mathbf{b}_i \big), $$
(54)

where the adjoint vector λ is computed at the cost of only a single solution of the adjoint equation

$$ \label{eq:adjoint} \mathbf{A}^\text{T} \boldmath{\lambda} = \mathbf{D}^\text{T} \frac{\left( \mathbf{y}^\text{M} - \mathbf{y} \right)} {\left\Vert \mathbf{y}^\text{M} \right\Vert^2}. $$
(55)

5.3 Remarks

In principle, if a small number of the time steps is used, the system matrix in (37) is of moderate dimensions and its inverse can be computed and used directly. However, in off-line identification, in the case of a dense time discretization or a longer sampling time, the system can become prohibitively large and computationally hardly manageable in a direct way. In such cases, the system matrix, which is a block matrix composed of lower triangular matrices, can be rearranged into the lower triangular block form that can be exploited by a specialized linear solver (like block forward-substitution or dynamic programming (Adams and Doyle 2002; Uhl 2007)) to reduce the numerical costs of the solution. Despite the inherent ill-conditioning of the system, application of such a solver is facilitated by the fact that both the matrix and the right-hand side vector are computed based on the FE model of the structure, and so they include only numerical errors, which are usually several orders of magnitude smaller than measurement errors. On the other hand, the left-hand side vector of (40) contains the measurement data and hence it can be contaminated with significant measurements errors. Thus, the results of any identification procedure based on a solution of (40) may suffer from instability, even if a regularization procedure is used.

Furthermore, given the FE model of the undamaged structure, the proposed method can be used online by repetitive applications in a moving time window (Zhang et al. 2010), that is by replacing the measured structural response \(\mathbf{y}^\text{M}\) in (43) with \(\mathbf{y}^{\text{M}(n)} - \bar{\mathbf{y}}^{(n)}\), where \(\mathbf{y}^{\text{M}(n)}\) is the response measured in the nth time window and \(\bar{\mathbf{y}}^{(n)}\) is the free vibration response of the undamaged structure caused by nonzero initial conditions at the beginning of the window. These initial conditions and the corresponding free vibrations can be computed using the FE model of the undamaged structure, provided the moving masses and the virtual distortions in the previous windows are already identified.

If the system parameters are known, the virtual distortions in (35) vanish, and the proposed method can be also used for identification of the moving masses only.

6 Numerical example

In this section, a multi-span frame structure is used to validate the proposed method for simultaneous identification of moving masses and damage. Measurement error and three types of model errors are taken into account in order to test the robustness of the method.

6.1 Structure and moving masses

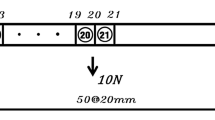
Figure 3 shows the model of the considered three-span frame structure. It is made of steel with Young’s modulus 2.15 ×1011 N/m2 and a density of 7.8 ×103 kg/m3; it has a uniform mass distribution of 15.3 ×103 kg/m and a simplified rectangular cross-section of b×h = 0.89 m × 2.21 m, so that the second moment of area is 0.8 m4. It is 200 m long; each of the two side spans is 50 m long. Each of the two piers is 20 m high and has the second moment of area of 0.16 m4.

Fig. 3
figure 3

Damaged three-span frame structure and three moving masses

Full size image

Three moving masses \(m_1 = 71.2 \times 10^3\) kg, \(m_2 = 60 \times 10^3\) kg and \(m_3 = 53 \times 10^3\) kg pass over the structure with constant velocities of v 1 = 34 m/s, v 2 = 34 m/s and v 3 = − 30 m/s. The initial positions of the masses are x 1,0 = − 3 m, x 2,0 = 0 m and x 3,0 = 200 m. Three strain sensors are employed: s 1 at the location of 65.2 m, s 2 at 95.2 m and s 3 at 145.2 m, as shown in Fig. 3. The sensors are placed at the bottom surface of the beam, so that the distance to the neutral axis is 0.5h = 1.105 m.

6.2 Measurement and model errors

Measurement errors of the simulated measurement data \(\mathbf{y}^\text{M}\) are modeled by adding an uncorrelated Gaussian noise at \(k_\text{n}\) rms level, that is

$$ \mathbf{y}^\text{M}\, \leftarrow \, \mathbf{y}^\text{M} + k_\text{n} \boldsymbol{\eta} \sqrt{\frac{\Vert\mathbf{y}^\text{M}\Vert^2}{n_\text{a}n_\text{t}}}, $$
(56)

where \(\boldsymbol{\eta}\) is a column vector of the same length as \(\mathbf{y}^\text{M}\) (that is, \(n_\text{a}n_\text{t}\)), whose elements are random numbers independently drawn from \(\text{N}(0,1)\). Altogether, three noise levels are used: \(k_\text{n} \in \left\{0\%,5\%,10\%\right\}\).

The influence of model error is tested below by using a different FE model of the structure for identification purposes than for the generation of the simulated measurements. For identification purposes, the beam is divided into 20 elements of 10 m each; each of the two piers is divided into two elements of 10 m (the original mesh). These values are chosen based on Law et al. (2004), where it is tested that a minimum of eight finite elements have to be used to model a single-span bridge deck for moving force identification. As described above, the moving masses are assumed to attach directly to the beam. This model is modified in order to generate the simulated measurements. The three following types of modifications are considered:

  • Type I, which is modification of the stiffness of all the elements. More precisely, uncorrelated Gaussian modifications with mean − 2% and standard deviation 5% are used, as due to both aging and initial model inaccuracies.

  • Type II: a mass-spring vehicle model is used instead of the simple moving mass, see Fig. 4.

  • Type III: a four times finer FE mesh is used, that is each of the 10 m elements is further divided into four equal elements of 2.5 m.

Fig. 4
figure 4

Type III model error: a mass-spring vehicle model is used instead of a simple moving mass

Full size image

For Type II model error, the parameters of the mass-spring vehicle model are chosen as in Au et al. (2004; Sheng et al. (2006): the stiffness is 286×106 N/m and the damping is 2.8×106 Ns/m. Figure 5 compares the responses obtained using the original undamaged structure, as well as the same structure with Type III model error and with Type II+III model errors. For a flat beam considered in this paper, the discrepancies between the responses obtained from the mass-spring vehicle model and those from the simple mass model are small. Similarly, noticeable effects of element mesh, like Type III model error, occur only at the times when the vehicles pass directly over the sensors: the finer mesh better reflects the local high-frequency components of the response. These local vibrations decrease soon after the vehicle passes by the sensor. Therefore, in order to improve the accuracy and decrease the influence of Type III model error, the local vibrations can be removed from the measurements by modifying the original objective function in (43) as follows:

$$ \label{eq:objtwe} f\big(\mu_1^\star, \ldots, \mu_{n_\text{m}+n_\text{e}}^\star\big) = \frac{1}{2}\frac{\left\Vert (\text{diag}\,\mathbf{w}) \left(\mathbf{y}^\text{M} - \mathbf{y}\right) \right\Vert^2} {\left\Vert (\text{diag}\,\mathbf{w}) \mathbf{y}^\text{M} \right\Vert^2}, $$
(57)

where w is a binary weighting vector, which contains only 1s with the exception of the time steps at which the vehicles are within a certain distance from any of the sensors (±2.5 m is used in this paper).

Fig. 5
figure 5

Responses of the undamaged system simulated using different meshes and vehicle models: sensors s 1, s 2 and s 3

Full size image

6.3 Identification cases

The following six cases are discussed to test the method proposed in this paper:

  1. 1.

    The structure is assumed to be undamaged. Only the moving masses are identified. Measurement error is simulated at 5% rms level. No model error is assumed.

  2. 2.

    Two pier elements (nos. 21 and 23) are damaged with the damage extents μ 21 = 0.4 and μ 23 = 0.7. The moving masses and the damage extents are identified simultaneously. The damage location is limited to the four pier elements of the original mesh, so that four stiffness modification coefficients are used in optimization, besides the three variables related to the masses. In this way, the exact number of the damaged elements and their locations are treated as unknown and also identified. Measurement error at 5% rms level and no model error are used.

  3. 3.

    As in Case 2, but Type I model error is additionally simulated, see Fig. 6 (left). The damage extents listed above in Case 2 relate to the element stiffnesses in the modified model, so the to-be-identified damage extents in Case 3 are slightly different, as they include the model error besides the damage.

  4. 4.

    As in Case 2, but model error Type II+III is used, that is the finer mesh and the mass-spring vehicle model are used to generate the simulated measurements, and no measurement error is considered. Identification of masses and damages is performed via (43), that is using all the responses without removing the local vibrations.

  5. 5.

    As in Case 4, but local vibrations are removed from the responses via (57) and measurement error is simulated at 5% rms level.

  6. 6.

    As in Case 5, but model error I+II+III is used, see Fig. 6 (right) for the stiffness modifications, and measurement error is simulated at 10% rms level. Local vibrations are removed from the responses via (57).

In all cases, the dynamic responses of the sensors are calculated using the Newmark integration method with the parameters α = 0.25 and β = 0.5. The integration time step equals 0.01 s (100 Hz sampling frequency). A total of 200 time steps is used, so that the sampling time interval is 2 s. The simulated noise-contaminated sensor responses in Cases 1 and 2 are shown in Fig. 7.

Fig. 6
figure 6

Stiffness reduction levels of the elements: (left) original mesh (Type I model error); (right) fine mesh (Type I+III model error)

Full size image
Fig. 7
figure 7

Simulated strain responses of the damaged and the intact systems in identification Cases 1 and 2. Simulated measurement noise at 5% rms level

Full size image

The following subsections discuss the identification in the six mentioned cases. The mass identification results are assessed by their relative accuracy, while the damage identification results are more naturally assessed in terms of their absolute accuracy (percentage points).

6.4 Moving mass identification (Case 1)

First, the moving masses are identified using a direct solution of (40), where the virtual distortions κ 0 are assumed to vanish. For a unique solution, at least three sensors are necessary. The pseudo-loads p are computed separately for the noise-free and the noise-contaminated measurements, see Fig. 8. The truncated singular value decomposition (TSVD) is used. The corresponding regularization levels (the number k of the truncated singular values) were determined using the L-curve technique (Jacquelin et al. 2003), that is by weighing in the log-log scale the residual of (40) vs. the norm of the first differences of the pseudo-load \(\Vert \mathbf{Lp} \Vert\). The L-curves are depicted in Fig. 8 (top) and attest that the (40) is seriously ill-conditioned. Moreover, consistently large values of the regularizing term \(\Vert \mathbf{Lp} \Vert\) suggest that it is impossible to get accurate results even at the optimal regularization level. In the noise-free case, the optimum regularization level is k = 29. The corresponding computed pseudo-load is shown in Fig. 8 (bottom left); the end part diverges suddenly from the actual mass-equivalent pseudo-force. With noise contamination, the pseudo-load is computed at the optimal value of k = 269 and shown in Fig. 8 (bottom right); both the front and the end parts diverge largely from the actual values. Table 1 lists the masses identified using (24), where the accelerations are computed via (36). The errors confirm that the result can be very sensitive to the disturbances of the measured response.

Fig. 8
figure 8

Case 1, three sensors. Moving load identification by a direct solution of (40): (top left) L-curve, noise-free measurements; (top right) L-curve, 5% rms measurement noise; (bottom left) computed pseudo-loads, noise-free measurements; (bottom right) computed pseudo-loads, 5% rms measurement noise. L is the matrix of the first differences. “estimate i” and “actual i” denote the ith estimated and actual pseudo-loads

Full size image
Table 1 Case 1
Full size table

In comparison, the identification via (43) turns out to be robust to noise. Moreover, the masses are accurately identified using a single sensor only (s 1), the results are listed in Table 1. The initial trial values of the moving masses are computed via (41); in each optimization step, the pseudo-load p is calculated fast using the moving dynamic influence matrix \(\mathbf{D}^\text{mm}\) by (37), which reduces to \([\mathbf{I}+\mathbf{m}\mathbf{D}^\text{mm}]\mathbf{p} = \mathbf{mg}\). The objective function is optimized using the function ’fmincon’, which is a part of the Matlab optimization toolbox. The pseudo-loads identified using the noise-contaminated measurements are compared with the actual pseudo-loads in Fig. 9; the results are very satisfactory under 5% rms noise pollution, especially in comparison to Fig. 8 (bottom right).

Fig. 9
figure 9

Case 1, single sensor s 1. Pseudo-loads, actual and identified by (43); “estva i” and “actva i” denote the ith estimated and actual pseudo-load

Full size image

6.5 Simultaneous identification of moving masses and damages (Cases 2–6)

The damage is limited to the two piers, that is to the respective four finite elements of the original mesh. Together with the three moving masses (mass modification coefficients), seven variables have to be identified by minimizing the objective function (43) or (57). Responses of only two sensors are used for that purpose (s 1 and s 3); the initial trial mass values are estimated via (41).

The identification results in Case 2 (5% measurement noise, no model error) are shown in Table 2. The three moving masses and four potential damages are identified accurately. As only two damages were actually assumed, the optimization allowed their number and location (limited to the four considered pier elements) to be identified as well. The results are relatively insensitive to the measurement error.

Table 2 Case 2
Full size table

The identification results in Cases 3–5 are shown in Table 3. The results confirm that the model error of Type I influences the accuracy of damage identification (Case 3), but both the damage and moving masses can be identified with acceptable accuracy even with an additional measurement error. For the model error of Type III (finer mesh), coupled with Type II (mass-spring vehicle model), the direct use of the simulated measurements in (43) results in poor accuracy even without any measurement error (Case 4). However, simple filtering of the local vibrations via (57) dramatically improves the accuracy to the level attained with Type I model error (Case 5, 5% measurement error included). These results suggest that in practice (57) should be always preferred over (43).

Table 3 Cases 3–5
Full size table

In the last test (Case 6), all three types of model errors are used together with the measurement error at 10% rms level. The identification is performed via (57). The results are listed in Table 4, where each actual damage extent is computed as an average of the damage extents of the four involved elements of the finer mesh. Given all the simulated errors, the results are of acceptable accuracy, which is not significantly worse than in the previously tested cases.

Table 4 Case 6
Full size table

7 Discussion

Section 2 discusses the VDM-based approach to modeling of damages. Although pseudo-loads could be directly used to model the damages via (10), the advantage of virtual distortions and modeling via (17) lies in

  1. 1.

    a smaller number of the distortions of an element in comparison to the number of its DOFs;

  2. 2.

    the intuitiveness of the relation between the stiffness modification and the corresponding virtual distortions, which is especially apparent in the case of a truss element;

  3. 3.

    natural gradation of importance of the virtual distortions, which is related to the order of the distortion (the magnitude of the corresponding eigenvalue) and to the excitation. Simulation or common engineering sense can be often used to determine which distortions of an element are dominant in its response and which are insignificant and can be thus neglected.

Besides damage extents, this paper treats moving masses as the optimization variables. In other research on moving load identification, the interaction forces between the structure and the masses are usually used as the unknowns. In these approaches, the forces-time histories in each time step are in general assumed to be independent, so that, in order to ensure a unique solution, the number of sensors must not be smaller than the number of the moving masses. Since such an identification is equivalent to a deconvolution, it is usually highly ill-conditioned and a numerical regularization is required. The regularization makes use of a priori assumptions about force-time histories, which usually concern their magnitude or smoothness (Tikhonov regularization) or limit the dimensionality of the solution space via a low-dimensional approximation. These assumptions are rather numerical than physical and so they cannot provide for missing sensors. By contrast, if the masses are treated as optimization variables, the forces-time histories in all time steps are coupled to the structural response and so cease to be independent. This kind of an assumption is physical and so the number of sensors can be decreased, as illustrated in the numerical example in Section 6.4, where a single sensor is used to identify accurately three moving masses, see Table 1, Figs. 8 and 9. In Section 6.5, two sensors are used to identify accurately seven unknowns (three masses and four damage extents), even despite the three concurrently used types of model errors and 10% measurement error.

It should be noted that before any practical application in bridge traffic monitoring, more research will have to be performed, e.g. to test multi-DOF vehicle models, more advanced bridge models and to confirm the locality of the effects of mesh-related model errors. Optimization of sensor number and placement is also an important problem, which affects the accuracy and resolution in most global methods of structural health monitoring.

8 Conclusion

Based on the virtual distortion method (VDM), this paper presents an effective method for simultaneous identification of moving masses and structural damage, which treats the masses and damage extents as the optimization variables. By an analogy to the dynamic influence matrix known in the VDM, the paper introduces the concept of the moving dynamic influence matrix, which allows the numerical costs of identification to be significantly reduced: the response of the system can be computed quickly without the need for numerical simulations and a repeated assembly of the time-variant mass matrix in each time step. A fast sensitivity analysis of the identification problem is used based on the adjoint method. The approach is tested numerically: four damages and three moving masses are identified using two sensors only. The identification error does not exceed 9% (4% on average), despite 10% simulated measurement error and three concurrently used types of model error.

The research is ongoing to investigate the ultimate accuracy and resolution of the method, as well as to introduce more advanced bridge and vehicle models.