Analysis of Characteristics of Two-Layer Convective Flows with Diffusive Type Evaporation Based on Exact Solutions

Abstract

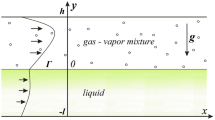
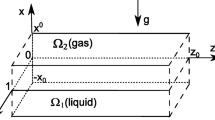
The theoretical approaches for mathematical modelling of the convective flows with mass transfer through the liquid–gas interface are discussed. The special attention is payed to modelling with use of the classical Boussinesq approximation of the Navier–Stokes equations. The diffusion equation and the effects of thermodiffusion and thermal diffusivity (the Soret and Dufour effects) are taken into account additionally to describe vapor and heat transfer processes in the gas-vapor phase. The use of the Oberbeck–Boussinesq equations allows one to apply the group-analytical methods in the theory of the evaporative convection and to construct the exact solutions of special type of the governing equations. Joint flows of the evaporating liquid and gas-vapor mixture are studied with the help of a partially invariant solution for the convection equations. The 2D and 3D solutions are demonstrated to simulate two-phase flows in the infinite channels with interface being under action of a longitudinal temperature gradient and perpendicularly directed gravity field. In the present paper the fluid flows with diffusive evaporation/condensation in the terrestrial and microgravity conditions are studied in the steady case. The new results obtained for combined thermal regime on the external rigid boundaries are presented.

Appendices

Appendix 1

When constructing the solution the case with the constant evaporation mass flow rate M = const is considered. The deceptively simple case allows one to perform the comparison with the values of M obtained in experiments and presented as trendlines (Goncharova et al. 2015).

Note that if the Dufour and Soret effects are taken into account simultaneously in boundary conditions for the temperature and vapor concentration (2.12) and (2.15), then these conditions can be replaced by equalities

$$ \frac{\partial T_{2}}{\partial n} = 0, \quad \frac{\partial C}{\partial n} =0. $$

(A.1)

Due to conditions (A.1) we have ${a_{2}^{2}} = 0$, b₂ = 0 and

$$ \begin{array}{@{}rcl@{}} {c_{6}^{2}} &=& - \frac{(x^{0})^{4}}{24} \frac{g}{\nu_{2}} E_{1} E_{2} - \frac{(x^{0})^{3}}{6} E_{2}{c_{1}^{2}}\\ &&- \frac{(x^{0})^{2}}{2} E_{2}{c_{2}^{2}} - x^{0}E_{2}{c_{3}^{2}}, \end{array} $$

where coefficients E₁, E₂ and B₁ are expressed in the following form:

$$ E_{1} = \beta_{2}A + \gamma b_{1}, \ \ E_{2}= \frac{b_{1}}{D} -\alpha B_{1}, \ \ B_{1} = \frac{DA-\chi_{2}\delta b_{1}}{D\chi_{2}(1-\alpha\delta)} . $$

Continuity conditions for the velocity and temperature (2.11) at the interface result in equalities of coefficients ${c_{3}^{1}} = {c_{3}^{2}}$, ${c_{5}^{1}} = {c_{5}^{2}}$.

Parameter ${a_{2}^{1}}$ is defined by relation ${a_{2}^{1}}= (A-A_{1})/x_{0}$ owing to linear temperature distribution (2.13) on the lower wall x = −x₀.

Heat balance condition (2.8) leads to the following equalities:

$$ \begin{array}{@{}rcl@{}} \kappa_{1} {a_{2}^{1}} -\kappa_{2} {a_{2}^{2}} -\delta\kappa_{2} b_{2} &=&0,\\ \kappa_{1} {c_{4}^{1}} -\kappa_{2} {c_{4}^{2}} -\delta\kappa_{2} {c_{6}^{2}} &=& -LM, \end{array} $$

(A.2)

where the mass flow rate of evaporating liquids is determined by relation $M = -D\rho _{2}\left ({c_{6}^{2}}+\alpha {c_{4}^{2}}\right )$ obtained from the mass balance equation (2.9). Since ${a_{2}^{2}} = b_{2} = 0$ the first condition in Eq. A.2 implies that ${a_{2}^{1}} = 0$. Consequently, equality of the temperature gradients on the lower wall and the interface is fulfilled: A₁ = A. The second condition in (A.2) allows one to express constant ${c_{4}^{1}}$:

$$ {c_{4}^{1}}= \frac{LD\rho_{2}\left( {c_{6}^{2}}+\alpha {c_{4}^{2}}\right)\kappa_{2} {c_{4}^{2}} + \delta\kappa_{2} {c_{6}^{2}}}{\kappa_{1}} . $$

Condition for saturated vapor concentration (2.10) has as a consequence the relations b₁ = C_∗ε_∗A and ${c_{7}^{2}} = C_{*}\left (1+\varepsilon _{*}{c_{5}^{2}}\right )$.

Dynamic conditions (2.7) defines correlations between coefficients ${c_{1}^{1}}$ and ${c_{1}^{2}}$, ${c_{2}^{1}}$ and ${c_{2}^{2}}$:

$$ {c_{2}^{1}}=\rho\nu {c_{2}^{2}}+ \frac{\sigma_{T} A}{\rho_{1}\nu_{1}} , \quad {c_{1}^{1}}=\rho\nu {c_{1}^{2}}. $$

Notation ρ and ν have been introduced in “??” (see formula (2.8)).

Integration constant ${c_{1}^{2}}$, ${c_{2}^{2}}$, ${c_{3}^{2}}$ are determined as a solution of the equation system obtained from the no-slip conditions on both walls of the channel (2.14) and additional condition (3.10):

$$ \begin{array}{@{}rcl@{}} &&\frac{{x_{0}^{2}}}{2} \rho\nu {c_{1}^{2}} -x_{0}\rho\nu {c_{2}^{2}} + {c_{3}^{2}} = \frac{\sigma_{T} A}{\rho_{1}\nu_{1}} x_{0}+ \frac{g\beta_{1}A}{6\nu_{1}} {x_{0}^{3}},\\ &&\frac{(x^{0})^{2}}{2} {c_{1}^{2}} +x^{0} {c_{2}^{2}} +{c_{3}^{2}}=- \frac{g(x^{0})^{3}}{6\nu_{2}} E_{1},\\ &&\frac{(x^{0})^{3}}{6} {c_{1}^{2}} + \frac{(x^{0})^{2}}{2} {c_{2}^{2}} + x^{0} {c_{3}^{2}} = \frac{Q}{\rho_{2}} -\frac{(x^{0})^{4}}{24} \frac{g}{\nu_{2}} E_{1}. \end{array} $$

Knowing ${c_{1}^{2}}$, ${c_{2}^{2}}$, ${c_{3}^{2}}$, constants ${c_{1}^{1}}$, ${c_{2}^{1}}$, ${c_{3}^{1}}$, ${c_{6}^{2}}$ can be calculated.

Then, constant ${c_{4}^{2}}$ is defined with the help of condition of zero heat flux on the upper wall x = x⁰ (the first equality in Eq. A.1):

$$ \begin{array}{@{}rcl@{}} \displaystyle {c_{4}^{2}}&=&- \frac{(x^{0})^{5}}{120} \frac{4g}{\nu_{2}} B_{2} E_{1} - \frac{(x^{0})^{4}}{24} \frac{g}{\nu_{2}} B_{1} E_{1}\\ &&+ \frac{(x_{0})^{3}}{6} B_{1}{c_{1}^{2}} - \frac{(x_{0})^{2}}{2} B_{1}{c_{2}^{2}}. \end{array} $$

Now value of ${c_{4}^{1}}$ can be found through known ${c_{6}^{2}}$ and ${c_{4}^{2}}$.

And finally, to define constant ${c_{5}^{1}}$ condition (2.13) is used:

$$ \begin{array}{@{}rcl@{}} {c_{5}^{1}}&=&T_{10}+ \frac{{x_{0}^{5}}}{120\chi_{1}} \frac{g\beta_{1} A^{2}}{\nu_{1}} - \frac{{x_{0}^{4}}}{24\chi_{1}} A{c_{1}^{1}}\\ &&+ \frac{{x_{0}^{3}}}{6\chi_{1}} A{c_{2}^{1}} - \frac{{x_{0}^{2}}}{2\chi_{1}} A{c_{3}^{1}} +{c_{4}^{1}} x_{0}. \end{array} $$

It allows one to found successively ${c_{5}^{2}}$ and ${c_{7}^{2}}$.

The pressure functions p_i are defined up to an additive constants ${c_{8}^{i}}$. Without loss of generality we can put the constants to be equal to zero.

Appendix 2

The physico-chemical parameters of working fluids are presented below in the order {HFE-7100, nitrogen} (or only HFE-7100) (Weast 1979; Lyulin et al. 2009):

$$ \begin{array}{@{}rcl@{}} &&\rho = \{1.5\cdot 10^{3}, 1.2\} kg/m^{3};\\ &&\nu = \{0.38\cdot 10^{-6}, 0.15\cdot 10^{-4}\} m^{2}/s;\\ &&\beta = \{1.8\cdot10^{-3}, 3.67\cdot10^{-3}\} K^{-1}; \\ &&\chi = \{0.4\cdot 10^{-7}, 0.3\cdot 10^{-4}\} m^{2}/s;\\ &&\kappa = \{0.07, 0.02717\} W/(m\cdot K);\\ &&\sigma_{T} = 1.14\cdot10^{-4} N/(m\cdot K);\\ &&D = 0.7\cdot10^{-5} m^{2}/s;\\ &&L = 1.11\cdot 10^{5} W\cdot s/kg;\\ &&C_{*} = 0.45;\\ &&\gamma = -0.5;\\ &&\varepsilon_{*} = 0.04 K^{-1};\\ &&\text{Dufour coefficient}~ \delta = 10^{-5} K;\\ &&\text{Soret coefficient}~ \alpha = 5\cdot 10^{-4} K^{-1}. \end{array} $$