Psychometric functions for detection and discrimination with and without flankers

Abstract

Recent studies have reported that flanking stimuli broaden the psychometric function and lower detection thresholds. In the present study, we measured psychometric functions for detection and discrimination with and without flankers to investigate whether these effects occur throughout the contrast continuum. Our results confirm that lower detection thresholds with flankers are accompanied by broader psychometric functions. Psychometric functions for discrimination reveal that discrimination thresholds with and without flankers are similar across standard levels, and that the broadening of psychometric functions with flankers disappears as standard contrast increases, to the point that psychometric functions at high standard levels are virtually identical with or without flankers. Threshold-versus-contrast (TvC) curves with flankers only differ from TvC curves without flankers in occasional shallower dippers and lower branches on the left of the dipper, but they run virtually superimposed at high standard levels. We discuss differences between our results and other results in the literature, and how they are likely attributed to the differential vulnerability of alternative psychophysical procedures to the effects of presentation order. We show that different models of flanker facilitation can fit the data equally well, which stresses that succeeding at fitting a model does not validate it in any sense.

Studies on lateral interactions have shown that the contrast threshold for detection of a target varies when it is measured in the presence or in the absence of flanking above-threshold stimuli. The magnitude and sign of this variation are, above all else, subject dependent, but they also depend on spatial frequency, visual eccentricity, presentation duration, or on the precise location, size, orientation, contrast, or onset asynchrony of the flankers (Adini, Sagi, & Tsodyks, 1997; Cass & Spehar, 2005; Giorgi, Soong, Woods, & Peli, 2004; Polat, 2009; Polat & Sagi, 1993, 1994a, 1994b, 2006; Shani & Sagi, 2005; Solomon & Morgan, 2000; Solomon, Watson, & Morgan, 1999; Tanaka & Sagi, 1998; Williams & Hess, 1998; Woods, Nugent, & Peli, 2002), and also on the paradigm used in the experiments (García-Pérez, Giorgi, Woods, & Peli, 2005).

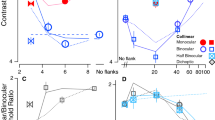
Although contrast detection threshold was traditionally the only parameter of concern in these studies, Petrov, Verghese, and McKee, (2006) and Shani and Sagi (2006) reported that lower thresholds in foveal presentations with flankers are accompanied by a flattening of the psychometric function. Other studies on the peripheral vision of patients with central field loss and age-matched normals have also shown a consistent flattening of psychometric functions without strong effects on detection thresholds (Alcalá-Quintana, Woods, Giorgi, & Peli, 2010). Interestingly, this flattening can also be observed in results reported by authors who failed to notice the outcome. For instance, García-Pérez et al. (2005) estimated psychometric functions with and without flankers in 16 different conditions for each of four observers at 4 deg of eccentricity, and their analysis focused as usual on a comparison of threshold estimates. Yet, their Fig. 2 showed sample data and fitted psychometric functions that seem to corroborate the claims of Petrov et al. (2006) and Shani and Sagi (2006). The broader picture is shown here in Fig. 1, which shows the relation between threshold and support (a measure of spread that is an inverse function of the usual slope parameter) with and without flankers in the data of García-Pérez et al. (2005). Because the effect of flankers varied with spatial and temporal paradigms, data from each condition are plotted separately in Fig. 1a, b. The left panels show thresholds with flankers against thresholds without flankers, where it can be noted that facilitation is not observed in spatial 2AFC but is prevalent in temporal 2AFC. The center panels show that the effect of flankers is consistent across paradigms in producing a flattening of the psychometric function (i.e., an increase in its support); finally, the right panels show that lower thresholds in the presence of flankers are associated with flatter psychometric functions only under temporal 2AFC.

Fig. 1

Effect of the presence of flankers under spatial (a) or temporal (b) 2AFC paradigms in the study of García-Pérez et al. (2005). The left panels show the relation between detection threshold in the absence of flankers and detection threshold in the presence of flankers for each of four observers (marked with different symbols) and conditions (largely unmarked). Open symbols represent conditions in which the collinear flankers were co-oriented with the target; solid symbols represent conditions in which they were cross-oriented. Data points below the diagonal identity line indicate flanker facilitation, and seem to occur only with temporal 2AFC. The center panels show the relation between the support of Ψ in the absence of flankers and its support in the presence of flankers. Graphical conventions are the same as before. Support is inversely related to slope and reflects the width of the nonasymptotic region of the psychometric function (Fig. 2 for a detailed explanation). With only rare exceptions, data points lie well above the diagonal regardless of psychophysical paradigm, indicating that the support of Ψ is larger (i.e., the function is flatter) in the presence of flankers than it is in the corresponding condition without flankers. The right panels show the relation between support and threshold. Solid symbols come from psychometric functions with flankers, open symbols come from psychometric functions without flankers, and data from different observers are plotted with different symbols. The presence of flankers reduces threshold and increases the support of the psychometric function only under a temporal 2AFC paradigm

The data presented in Fig. 1 concur with the results of Petrov et al. (2006), Shani and Sagi (2006), and Alcalá-Quintana et al. (2010) in suggesting that the presence of flankers affects support more than threshold. Actually, Fig. 1 reveals that the only unique, strong, and consistent effect of the presence of flankers is a flattening of the psychometric function, but all these data reveal the effect of flankers on threshold and support only at threshold contrasts. Direct evidence on whether this flattening of psychometric functions occurs also at suprathreshold levels is lacking. Some studies have measured discrimination thresholds with and without flankers with an eye toward obtaining threshold-versus-contrast curves (TvC curves; see Adini & Sagi, 2001; Chen & Tyler, 2001, 2002, 2008; Zenger-Landolt & Koch, 2001), but they provide only indirect evidence that the psychometric functions for discrimination have a larger support (i.e., they are flatter) in the presence of flankers. Nonetheless, it is worth discussing what the data reported in those studies indicate, however indirectly, about the support of the psychometric functions at high contrast levels with and without flankers.

Interestingly enough, the TvC curves reported in these few studies show a large diversity of patterns as to how contrast discrimination thresholds vary with standard contrast (i.e., with the contrast of the standard stimulus) with and without flankers. For instance, Zenger-Landolt and Koch (2001; see their Fig. 3) and Adini and Sagi (2001; see their Fig. 2b) reported TvC curves in the presence of flankers that were substantially above those for the target alone, and a large fraction of the curves had a second dipper in the high-contrast region. These results thus suggest that psychometric functions with flankers are flatter,¹ although they are not uniformly so along the contrast continuum. Yet, a different pattern was reported by Chen and Tyler (2001, 2002, 2008). In this case, TvC curves with flankers were generally merely shifted to the left of TvC functions without flankers so that the TvC function with flankers lay below that without flankers in the low-contrast region and then crossed over and lay above that with flankers in the high-contrast region. Chen and Tyler (2008) interpreted this pattern as indicating that flankers produce facilitation in the low-contrast region and inhibition (threshold elevation) in the high-contrast region. But these characteristics are also consistent with the notion that, with flankers, psychometric functions are steeper with low-contrast standards and flatter with high-contrast standards.

Fig. 2

Graphical interpretation of the parameters of the logistic Ψ resulting from insertion of Equation 3 into Equation 1. Parameter γ is valued at the guessing rate of .5 that applies in a 2AFC detection task, thus setting a lower horizontal asymptote at .5. Parameter λ is set at .02 so that the upper horizontal asymptote lies at 1 – λ = .98. Parameter θ (θ = –1.5 here) is the point at which Ψ evaluates to the midpoint between its asymptotes; that is, $\Psi \left( \theta \right) = \left( {1 - \lambda + \gamma } \right)/2$, as indicated by the dotted line in the graph; the location of Ψ relative to an arbitrary performance level π_T is given by x _T (in this illustration, x _T = –1.32 relative to π_T = .84; see the dashed line in the graph). The scale parameter β (β  =  0.2 here) indicates the width of the central 24.49% span of Ψ (see the horizontal segment drawn near the horizontal axis); our replacement parameter σ indicates the width of the horizontal region where Ψ spans a larger central percentage of its nonasymptotic regime. The percentage chosen determines the value of an auxiliary parameter δ, which is added to the lower asymptote and subtracted from the upper asymptote to draw the two solid horizontal lines across the graph (labeled γ + δ and 1 – λ – δ on the right of the graph). Each of these lines crosses Ψ at only one point, and the horizontal distance between those two points represents the support of Ψ (σ = 1.083 here). In this illustration, we set δ = .03 (yielding the width of the central 87.5% span of Ψ) so that the reference lines and crossings are visible; we advocate the use of $\delta = \left( {{1} - \lambda - \gamma } \right)/100$, so that δ = .0048 here, and σ thus measures the central 98% span of Ψ. Relative to this latter value for δ, the curve plotted here has σ = 1.838

Because of these discrepant results and also because the evidence that they provide about the effect of flankers on the support of the psychometric function is only indirect, the aim of the work described in the present article was to gather direct evidence on this issue. Thus, psychometric functions with and without flankers were estimated for detection and for discrimination at standard contrasts ranging from near detection threshold to well above detection threshold. And, in doing so, we paid particular attention to circumventing a problem of 2AFC methods that is often overlooked and that affects the estimated support (or flatness) of the estimated psychometric functions. Use of 2AFC tasks in contrast discrimination studies is potentially affected by so-called “order effects,” which show that the results differ according to whether the standard stimulus is presented in the first or second intervals of each 2AFC trial. Actually, psychometric functions separately fitted to data from either type of trial are generally laterally shifted away from the standard level and in opposite directions, with the consequence that a psychometric function fitted to aggregated data from both types of trials is flatter than either of its components (Alcalá-Quintana & García-Pérez, in press; García-Pérez & Alcalá-Quintana, 2010a; Ulrich & Vorberg, 2009). These separate psychometric functions can further show different supports, which complicates understanding what the psychometric function obtained from aggregated data across presentation orders represents. To say the least, this raises the question of which of them is the “true” psychometric function and, hence, which of them carries the actual discrimination threshold. Previous research on flanker facilitation effects discussed in the preceding paragraphs has overlooked this problem and, since psychometric functions were not directly measured, the magnitude of contamination by order effects is unknown. To circumvent at least the identified causes of order effects, our experiments were carried out using the strategy described in García-Pérez and Alcalá-Quintana (2010a). Specifically, capitalizing on Fechner’s (1860/1966) observation of an “interval of uncertainty” in which the observer cannot decide which stimulus has a higher contrast, we measured observers’ performance using Fechner’s amendment of the Method of Right and Wrong Cases, which consists of counting “the undecided case as half right and half wrong.” Fechner (p. 78) wrote that this strategy “is the only one which can also yield a basis for elimination and precise determination of the influences...which cause constant errors,” and it is implemented by allowing three response categories (“Interval 1”, “Interval 2”, and “I don’t know”; see also Urban, 1910). A reinterpretation of Fechner’s ideas in terms of signal detection theory was described by Watson, Kellogg, Kawanishi, and Lucas (1973) and is the basis for our method. Use of this method has been shown to eliminate the spurious flattening of psychometric functions due to order effects produced by response bias (Alcalá-Quintana & García-Pérez, in press; García-Pérez & Alcalá-Quintana, 2010a), and it also eliminates the interval bias that is for similar reasons typically observed in 2AFC detection tasks (García-Pérez & Alcalá-Quintana, 2010b).

Location and support of an arbitrary psychometric function

Because we will deal with detection and discrimination data, a formal characterization of the psychometric function Ψ that encases both situations would be useful. We will adopt the same formalism discussed in Alcalá-Quintana and García-Pérez (2004, 2005), but, to make this report self-contained, we will briefly repeat it here. The general mathematical form of Ψ is

$$\Psi (x) = \gamma + \left( {1 - \lambda - \gamma } \right) F\left( {x;\theta,\beta}\right), $$

(1)

where x = log(c), 0  ≤  c  ≤ 1 is Michelson contrast, λ is the lapsing rate, γ is the guessing rate (γ = 1/2 in 2AFC detection tasks), F is a monotone increasing function expressing how the probability of some relevant sensory event varies with x, and θ and β are the location and scale parameters of F, respectively.

To gain some flexibility, we will define the location of a psychometric function Ψ as the point x _T at which the probability of a correct response reaches some arbitrary level π_T (with $\gamma < {\pi_{\rm{T}}} < 1 - \lambda$); that is, x _T  =  Ψ^-1(π_T). Under this approach, x _T can be directly interpreted as a detection threshold, a PSE, or a reference point for a discrimination threshold under the conventional definitions—that is, the stimulus level at which the probability of a correct response is some conveniently chosen π_T. Thus, the detection threshold can be defined as x ₈₄  =  Ψ^-1(.84) on the psychometric function for detection (although other performance levels ranging from .75 to .94 have occasionally been used), the PSE is defined as x ₅₀  =  Ψ^-1(.5) on the psychometric function for discrimination, and the discrimination threshold is defined as the distance between x ₅₀ and x ₇₅ on the psychometric function for discrimination also (although, again, other performance levels ranging from .67 to .94 have occasionally been used in place of x ₇₅).

Similarly, and owing to difficulties interpreting and estimating slope parameters (García-Pérez & Alcalá-Quintana, 2005; see also Gilchrist, Jerwood, & Ismaiel, 2005), we will define the support σ of a psychometric function Ψ as the width of the range of contrasts, where Ψ shows nonasymptotic behavior. Formally, given some small $\delta \left( {0 < \delta < \left( {1 - \lambda - \gamma } \right)/2} \right)$,

$$ \sigma = {\Psi^{{ - 1}}}\left( {1 - \lambda - \delta } \right) - {\Psi^{{ - 1}}}\left( {\gamma + \delta } \right) $$

(2)

represents the horizontal range spanned by the nonasymptotic regime of Ψ—that is, the contrast range (in log units) within which the probability of a correct response varies between γ + δ (i.e., slightly above the lower asymptote) and 1 – λ – δ (i.e., slightly below the upper asymptote). When $\delta = \left( {1 - \lambda - \gamma } \right)/100$, σ measures support as the width of the central 98% span of Ψ.

When F in Equation 1 is given by the logistic function

$$ F\left( {x;{{\theta, \beta }}} \right) = \frac{1}{{1 + \exp \left[ { - \left( {x - {{\theta }}} \right)/{{\beta }}} \right]}}, $$

(3)

it can easily be seen that

$$ {x_{\rm{T}}} = {{\theta }} - {{\beta }}\;{ \ln }\left[ {\frac{{1 - \lambda - {\pi_{\rm{T}}}}}{{{\pi_{\rm{T}}} - \gamma }}} \right], $$

(4)

$$ \sigma = 2\;{{\beta }}\;{ \ln }\left[ {\left( {1 - \lambda - \gamma - \delta } \right)/\delta } \right]. $$

(5)

When ${\pi_{\rm{T}}} = \left( {1 - \lambda + \gamma } \right)/2$ (i.e., when π_T is the midpoint between the lower asymptote at γ and the upper asymptote at 1 – λ), Equation 4 yields π_T = θ so that θ can be interpreted as the point at which the probability of a correct response is midway between the floor performance level γ and the ceiling performance level 1 – λ. Similarly, when $\delta = \left( {1 - \lambda - \gamma } \right)/100$, Equation 5 reduces to $\sigma = 2\;{{\beta }}\;{ \ln }\left( {99} \right) \approx 9.19{{\beta }}$. Alternatively, when $\delta = 37.754\left( {1 - \lambda - \gamma } \right)/100$, Equation 5 reduces to σ = β so that β can be interpreted as the width of the central 24.49% span of Ψ. These characteristics are illustrated in Fig. 2 for a logistic Ψ with γ = .5 (for 2AFC detection tasks), λ = .02, β = 0.2 (yielding σ = 1.083 with δ = .03), and θ = –1.5 (yielding x _T = –1.32 relative to π_T = .84).

Experiments

The experiments for this investigation required estimating the psychometric function for detection of a target in the presence and also in the absence of above-threshold flankers. Also required was a contrast discrimination experiment involving a number of different standard contrasts—an experiment that also needs to be conducted in the presence and in the absence of the same flankers that were used in the detection experiment. These experiments were carried out in the two labs in which the authors work, using identical software but slightly different hardware. The details and results of these experiments are described next.

Apparatus and Stimuli

All experiments were controlled by PCs equipped with VisionWorks (Swift, Panish, & Hippensteel, 1997). In Madrid, stimuli were displayed on a 20-in. Clinton Monoray (Richardson Electronics Ltd., LaFox, IL) monochrome monitor (model M20ECD5RE, DP104 phosphor) with a spatial resolution of 1,024 × 768 pixels (horizontal × vertical), a luminance resolution of 2¹⁵ gray levels, and a frame rate of 127 Hz. The image area spanned 36.8 cm horizontally and 27.6 cm vertically, which subtended 20.85 × 15.71 deg at a distance of 100 cm. In Boston, stimuli were displayed in monochrome mode on an EIZO Flex-Scan FX·E7 color monitor with a spatial resolution of 1,024 × 600 pixels, a luminance resolution of 2¹⁵ gray levels, and a frame rate of 122 Hz. The image area spanned 40 cm horizontally and 23.4 cm vertically, subtending 22.62  ×  13.35 deg at a distance of 100 cm. The voltage-to-luminance nonlinearity was compensated for via look-up tables arising from a calibration procedure that rendered correlations of .999961 and .999983 (in Madrid and Boston, respectively) between actual and nominal luminance.

The target stimulus was a Gabor patch with a horizontal carrier of 2 c/deg and a circular Gaussian envelope with a standard deviation of 0.35 deg (resulting in half-amplitude spatial-frequency and orientation bandwidths of 0.792 octaves and 31.06 deg, respectively).² The target was created within a 98 × 98 pixel array (90 × 90 in Boston) and was thus truncated to approximately ±2.84 SDs of the Gaussian envelope. The stimulus was represented internally with 24.44 pixels per cycle of the carrier (22.48 in Boston) and was displayed with a mean luminance of 36 cd/m² (38 cd/m² in Boston) that blended in with a uniform background of the same mean luminance and covering the entire image area. A small black circle (2 pixels in radius) was permanently displayed at each of the four corners of the square area at which the target stimulus would appear, and the observers were asked to maintain fixation around the center of the area whose perimeter was thus marked. This fixation aid was not extinguished during stimulus presentation, and its perimetric location with respect to the target helped to prevent masking effects (see Summers & Meese, 2009). The standard stimulus in discrimination experiments was thoroughly analogous except that its contrast was fixed at the applicable level. Standard and target were separate stimuli whose contrasts were manipulated independently. The temporal course of stimulus presentation was a rectangular pulse of 181.1 msec (23 video frames) in Madrid and 180.3 msec (22 video frames) in Boston.

In separate blocks in each experiment, the stimulus field either consisted of the target (or the standard, when applicable) just described or included also two flanking Gabor patches of the same frequency, orientation, and size, but with a fixed suprathreshold Michelson contrast, c = .4, which were located to the left and right of the target (and standard, when applicable), centered 2 deg (i.e., four wavelengths) away from it, and displayed on both intervals of each 2AFC trial.³ Flankers were created within pixel arrays of the same size as those used to create the target (and the standard) so that the flankers and target (or standard) did not overlap spatially when presented simultaneously. Simultaneous presence of the flankers at a fixed contrast requires that some slots in the display look-up table be reserved for them. Thus, the flankers were displayed with a total of 126 fixed gray levels, whereas the target (or standard) was also displayed with 126 gray levels that were drawn from a palette of 2¹⁵ levels to render the contrast required for the presentation. To avoid differences in these respects between blocks with and without flankers, in the latter, the target (and the standard) was also displayed with 126 gray levels only.

Procedure

The monitor was allowed to warm up for no less than half an hour before any session started. Binocular viewing with natural accommodation and pupils was used. Observers sat 100 cm away from the display, and their heads were not restrained, although they were asked to maintain a fixed viewing distance throughout the experiment. The room was dark except for the light from the display monitor. The background luminance and the fixation aid were present throughout the experimental session.

All data were gathered using a temporal 2AFC paradigm. A trial consisted of two intervals; the target was displayed only in one of these (newly decided with equiprobability on each trial, but with the constraint that exactly half of the trials display the target in each interval), whereas the other interval displayed mean luminance (in detection experiments) or a standard of the required contrast. In sessions with flankers, these were present in both intervals. The two temporal intervals were marked by beeps of different pitch and were separated by a gap of 503.9 msec (64 frames) in Madrid or of 516.4 msec (63 frames) in Boston, with intertrial intervals of at least the same duration as the interstimulus intervals. The observer’s task was to indicate by a keypress the interval in which the target had been presented (in detection experiments) or the interval in which the stimulus had higher contrast (in discrimination experiments). If both intervals appeared to have displayed a stimulus with the same contrast (or a blank), observers were instructed to use a third, “don’t know” key to indicate their indecision.⁴ This event was recorded in the data file, but it also made the computer generate a random response so that the adaptive staircases to be described next could proceed. If the observers had missed a trial for whatever reason, they could use a fourth key to ask for the trial to be discarded and repeated (not necessarily immediately afterward). The session was self-paced; the next trial did not start until the observer had responded. This is the reason that intertrial intervals might have variable length, but are still with the minimum duration specified above.

Data were gathered using an adaptive method of constant stimuli governed by 1–up/1–down staircases. Full details and justification for the use of these staircases are given in García-Pérez and Alcalá-Quintana (2007b; see also García-Pérez & Alcalá-Quintana, 2005), but their setup is briefly described next. In detection experiments, steps up tripled the size of steps down (0.3 and 0.1 log units, respectively), and two separate staircases were interwoven that differed only by 0.05 log units in their starting points (log contrast of –1 versus –0.95)—that is, half the base step size of 0.1 log units used in each staircase, so that the two staircases ran on interlaced lattices. The two starting points represent contrast levels at which the target was well above threshold. The detection experiment was carried out first and thus helped select the set of standard contrasts to be used in the discrimination experiment. Each of the various standard contrast levels thus selected was used in a separate session of the discrimination experiment.

The discrimination experiment involved 12 standard levels placed around each observer’s detection threshold determined earlier. The levels used with each observer in the conditions with and without flankers are listed in Table 1 and are labeled from s ₁ to s ₁₂. Note that the spacing of standard levels around the detection threshold (which defines standard level s ₃) is finer than the spacing of standard levels well above the detection threshold: 0.1 log units between levels s ₁ and s ₆, 0.15 log units between levels s ₆ and s ₉, and 0.2 log units between levels above s ₉.⁵ The reason for these different spacings is that we wanted to evaluate discrimination performance when the standard level was within the nonasymptotic regime of the psychometric function for detection (standard levels s ₁ to s ₆) and also when the standard level was within the upper asymptotic regime of the psychometric function for detection (standard levels s ₇ to s ₁₂).

Table 1 Standard contrasts (designated s ₁ to s ₁₂) used in the discrimination experiment for each observer when the target is presented alone or with flankers. Each observer’s detection threshold in each condition, rounded to the nearest twentieth of a log unit (i.e., 1 dB), is s ₃

The setup of staircases in discrimination experiments varied with the contrast of the standard. When the standard was at or below 0.2 log units above the detection threshold (i.e., for standard levels between and including s ₁ and s ₅; see Table 1), one of the interwoven staircases used steps up that were triple the size of steps down (0.45 and 0.15 log units, respectively), whereas the other used steps up that were double the size of steps down (0.30 and 0.15 log units, respectively), and their respective starting points were 0.450 log units above and 0.525 log units below the contrast of the standard. At higher standard levels (s ₆ to s ₁₂), the interwoven staircases also had starting points that were 0.450 log units above and 0.525 log units below the contrast of the standard, but they applied inverse rules so that the first interwoven had steps up that were triple the size of steps down (0.45 and 0.15 log units, respectively), whereas the second had steps up that were one-third the size of steps down (0.15 and 0.45 log units, respectively).

Staircases in the detection experiment were set up to complete 250 trials each, and two separate 500-trial sessions were run so that the psychometric function for detection was estimated with data from 1,000 trials. When the standard in discrimination experiments was at or below the detection threshold (standard levels from s ₁ to s ₃), staircases were set up to complete 90 trials each; two pairs of interlaced staircases were interwoven in a 360-trial session, and two repeat sessions provided a total of 720 trials per standard level. When standard level was immediately above the detection threshold (standard level s ₄), staircases differed only in that they were set up to complete 125 trials each, so that a single session collected data from the 500 trials that would be used to estimate the psychometric function at this standard level. At the next standard level (designated s ₅), staircases ran for 110 trials and rendered data from 440 trials in a single session. At higher standard levels (designated from s ₆ to s ₁₂), each of the interlaced staircases completed 45 trials, and four pairs of interlaced staircases were interwoven in a single session to provide a total of 360 trials per standard level. These variations in the number of trials contributing to the estimation of psychometric functions for detection and discrimination fulfill requirements for precision contingent on the height of the lower asymptote of the psychometric function in each case (see García-Pérez & Alcalá-Quintana, 2005).

Observers completed the detection experiment (without and with flankers) first, and then proceeded to complete all of the discrimination sessions without flankers first, followed by the discrimination sessions with flankers. Sessions in the discrimination experiment were arranged in increasing order of standard level, but pauses of at least 10 min were given between consecutive sessions.

Data analysis

Data from each observer and condition were analyzed separately. Data from all applicable trials (in detection or discrimination with a given standard level, and with or without flankers) were pooled and binned by contrast level to fit a logistic psychometric function in each condition. In applying Fechner’s (1860/1966) “half right and half wrong” rule, half of the “don’t know” responses given at each contrast level were counted as correct, and the other half were counted as incorrect. The psychometric functions for detection had the general form in Equation 1 with F as in Equation 3, and maximum-likelihood estimates of their three parameters (λ, θ, and β, since γ = .5 is not a free parameter in this case) were obtained using NAG subroutine e04jyf (Numerical Algorithms Group, 1999), which uses a quasi-Newton algorithm and allows constrained optimization.⁶ We imposed the natural constraints β > 0 and θ < 0, and also 0 ≤ λ ≤ .06. Discrimination data at a given standard level were also fitted to the same general logistic function, and estimates of γ (which is a free parameter in this case), λ, θ, and β were similarly obtained with the additional constraint 0 ≤ γ ≤ .5. Once these functions had been fitted, detection thresholds relative to ${\pi_{\rm{T}}} = \left( {1 - \lambda + .5} \right)/2$ and measures of support with $\delta = \left( {1-\lambda -.5} \right)/100$ were obtained from the psychometric function for detection using the relations in Equations 4 and 5 above. Note, then, that detection thresholds are defined as the stimulus level for which performance is at the midpoint of the range of the psychometric function. The same Equations 4 and 5 were used with discrimination data, where PSEs were conventionally obtained relative to π_T = .5 and discrimination thresholds were obtained relative to π_T = .75, whereas measures of support were obtained making $\delta = \left( {1 - \lambda - \gamma } \right)/100$. Figure 3 illustrates all of these measures using sample psychometric functions for detection, near-threshold discrimination, and above-threshold discrimination.

Fig. 3

Graphical illustration of the estimates of detection threshold and support obtained from psychometric functions for detection (curve on the left), and the estimates of PSE, discrimination threshold, and support obtained from psychometric functions for discrimination near the detection threshold (second curve from the left) and at two different levels above the detection threshold (two curves on the right). For simplicity, this illustration assumes λ = 0. Discrimination thresholds relative to a 75%-correct performance level on the corresponding curve are given by the distance between the reference dashed and solid vertical lines for each curve; PSEs (the 50%-correct point in discrimination curves) are indicated by solid vertical lines

Detection data were also subjected to a second analysis by which the psychometric function was fitted using the denoising approach described in García-Pérez (2010). In practice, denoising merely implies (a) replacing computer-generated responses arising from the observer’s use of the “don’t know” key with wrong responses, and (b) fitting a general form for the psychometric function in which the lower asymptote is a free parameter ξ. For additional details, see García-Pérez (2010). Discrimination data were not denoised in any way.

Some of our analyses require tests of equality (e.g., whether discrimination thresholds with and without flankers are identical). In all of these cases, the Bradley–Blackwood test was used, which is a robust simultaneous test of equality of means and variances with paired data (Bradley & Blackwood, 1989).

Observers

Five experienced psychophysical observers with normal or corrected-to-normal vision participated in the study. Observers M1, M2, and M3 participated in Madrid; Observers B1, B2, and B3 participated in Boston. Observers M1 and B1 are the same person (one of the authors); Observers M2 (an author) and B2 were also aware of the design and goals of the study; the remaining observers (M3 and B3) were naive in all these respects. Prior to their participation, all observers read and signed an informed consent form that had been approved by the Institutional Review Board in accordance with NIH regulations.

Results

Estimated psychometric functions for detection

Figure 4a shows raw data and fitted psychometric functions for detection for each observer in each condition. Several aspects of these data are worth pointing out. First, B3 is the only observer showing threshold elevation in the presence of flankers, in an amount of 0.05 log units; the remaining observers did show some facilitation in an amount that varied between 0.02 log units (Observer B1) and 0.09 log units (Observer M1). Second, Observer M1 showed facilitation in the typical amount (a threshold reduction of 0.09 log units in the presence of flankers), whereas Observer B1 (who is indeed the same person, as indicated above) showed a smaller effect (0.02 units), although it is unclear whether this is simply a question of sampling error. At the same time, Observer B1 showed lower absolute sensitivity than did Observer M1: Detection thresholds for B1 were 0.15 log units higher without flankers and 0.22 log units higher with flankers. These differences in absolute sensitivity cannot be attributed to the different hues of the phosphors in each monitor (a yellowish-green phosphor for Observer M1 compared to an RGB white-looking phosphor for Observer B1), because contrast sensitivity in green and white monochromatic light is virtually identical, provided the mean luminance is matched (Nelson & Halberg, 1979; Watanabe, Mori, Nagata, & Hiwatashi, 1968; Zulauf, Flammer, & Signer, 1988). A more subtle difference in hardware seems to have produced these variations in absolute thresholds, but a discussion of this side issue (which has no impact on the paired comparisons involved in this study) is deferred to the Appendix.

Figure 4b shows analogous psychometric functions fitted to denoised data, which confirm the aforementioned points. In particular, estimates of threshold and support are virtually identical for each observer and condition whether they are obtained from raw data (Fig. 4a) or denoised data (Fig. 4b). Both approaches differ only as to how “don’t know” responses are treated: They are regarded either as half right and half wrong (Fig. 4a) or as wrong responses. As discussed in García-Pérez (2010), one of the advantages of denoising is that the free lower asymptote in the fitted psychometric function indicates compliance of the observer with the instructions to use the “don’t know” response key, something that is impossible to check out with raw data. A second advantage is that estimates of support from denoised data have smaller standard errors.

Fig. 4

Data and fitted logistic psychometric functions for detection of the target without flankers (open symbols and dashed curves) and with them (solid symbols and solid curves). To avoid clutter, data points are shown only if at least 10 trials had been administered at the applicable contrast level, but all data were used for parameter estimation. Part (a) shows results for raw data; part (b) shows results for denoised data. Each panel in each part shows results for a different observer, as indicated in the top left corner. Estimated parameters are given in the insets; parameter ξ in part (b) is an estimate of the lower asymptote for denoised data (see García-Pérez, 2010)

A summary picture of the relations between threshold and support with and without flankers is given in Fig. 5 in the same format used in Fig. 1, but for our raw (Fig. 5a) and denoised (Fig. 5b) data. In either case, our results show mild facilitatory effects of flankers (left panels in Fig. 5a, b), stronger effects on the support of the psychometric functions in the presence of flankers (center panels in Fig. 5a, b), and a lack of relation between threshold and support (right panels in Figs. 5a, b): The relation was negative but not significantly different from zero in the presence of flankers whether for raw data [r = –.74; 95% confidence interval (–.97, .18) in Fig. 5a] or for denoised data [r = –.62; 95% confidence interval (–.95, .38) in Fig. 5b], and a weaker sample correlation was also not significantly different from zero for the target alone whether for raw data (r = .20 in Fig. 5a) or for denoised data (r = .09 in Fig. 5b).

Fig. 5

Relation between detection thresholds with and without flankers (left panels), between support with and without flankers (center panels), and between support and detection threshold (right panels; solid symbols for the condition with flankers and open symbols for the condition without flankers) in the results shown in Fig. 4 for raw data (a) and denoised data (b). When larger than symbol size, error bars (vertical for estimated values along the vertical axes and horizontal for estimated values along the horizontal axes) are standard errors taken from García-Pérez (2010; see his Fig. 3) for raw or denoised estimates arising from sets of 1,000 trials

Estimated psychometric functions for discrimination

Figure 6 shows data and fitted psychometric functions for discrimination for each observer (rows) in each condition (distributed across two panels to reduce clutter). At low standard levels (between s ₁ and s ₆), for which the psychometric function for detection has not yet reached its upper asymptotic regime, the psychometric functions for discrimination have the high lower asymptote expected from the formal analysis in García-Pérez and Alcalá-Quintana (2007b); at higher standard levels (at and above s ₇), where detection performance is at its ceiling level, the lower asymptote of the psychometric function for discrimination is at or near zero. These characteristics hold with and without flankers.

Figure 7 compares the location and support of the psychometric functions for discrimination in the presence (solid symbols and curves) and in the absence (open symbols and dashed curves) of flankers at each standard level separately for the case of standard levels around the detection threshold (s ₁ to s ₆; Fig. 7a) and for the case of standard levels well above the detection threshold (s ₇ to s ₁₂; Fig. 7b). In the former case, the specific standard levels used in the presence and in the absence of flankers are generally different for any given observer (see Table 1) because they are defined relative to the detection threshold in each condition. For this reason, parameter estimates obtained with and without flankers are first plotted as a function of standard contrast in the top row of Fig. 7a. The left panel in the top row of Fig. 7a plots the PSE for each observer and standard level against the actual standard level, with open symbols when target and standard were presented alone and solid symbols when target and standard were presented with flankers. In principle, the PSE should match the standard level within sampling error in all cases, and the data bear this expectation with no apparent differences between conditions with and without flankers. The correlation between standard level and PSE in the absence of flankers was .995 (it was .991 with flankers), with the 95% confidence interval ranging from .990 to .998 (or from .981 to .995 with flankers); on the other hand, least-squares regression lines fitted to the data yielded intercepts of –0.112 without flankers and –0.068 with them that were not significantly different from zero [95% confidence intervals (–0.172, 0.052) without flankers and (–0.147, 0.010) with them] and slopes of 0.932 without flankers and 0.957 with flankers that were not significantly different from unity [95% confidence intervals (–0.202, 2.066) without flankers and (–0.505, 2.418) with them].

The center panel in the top row of Fig. 7a plots discrimination thresholds as a function of standard level for the same conditions for which PSEs were plotted in the left panel. As is clear from the sketch in Fig. 3, the distance between the PSE and the point that serves as a reference to define the discrimination threshold increases as the psychometric function flattens. Then, variations in the discrimination threshold (i.e., the distance between those two points) as a function of standard level are indirect indications of concomitant changes in the support of the underlying psychometric functions. A quick look at the center panel in the top row of Fig. 7a suffices to note that discrimination thresholds decrease as standard level increases and that the sets of conditions with and without flankers (solid and open symbols, respectively) do not seem to yield different outcomes. Quantitatively, the significant correlation between standard level and discrimination threshold in the absence of flankers was –.774 (it was –.722 with flankers), with the 95% confidence interval ranging from –.879 to –.598 (or from –.849 to –.516 with flankers).

Finally, the right panel in the top row of Fig. 7a shows how support varies with standard level, something for which the center panel provided only indirect evidence. The correlation between support and standard level was not significantly different from zero whether without flankers [open symbols; r = .219; 95% confidence interval (–.118, .511)] or with flankers [symbols; r = –.157; 95% confidence interval (–.462, .181)]. The different outlook given by the center and right panels in the top row of Fig. 7a clearly reveals that discrimination thresholds are only indirect and are somewhat inaccurate indices of how the support of the psychometric function varies with standard level. This is because at low standard levels, the psychometric functions for discrimination have asymmetric lower and upper asymptotes (see Fig. 6).

Fig. 6

Data (symbols) and fitted logistic psychometric functions (curves) for discrimination. Results for different standard contrasts are shown with different symbols and are separated into two columns of panels to reduce clutter (see the legend at the top of each column). Open symbols and dashed curves represent results without flankers; solid symbols and solid curves represent results with flankers. To avoid clutter, data points are shown only if at least 10 trials had been administered at the applicable contrast level, but all data were used for parameter estimation. Each row shows results for a different observer, as indicated in the top left corner in the panels on the left column

As mentioned previously, near-threshold standard levels were generally different with and without flankers for each observer, something that precludes a direct comparison of the characteristics of the psychometric functions with and without flankers. Nevertheless, the differences were generally small (see Table 1): 0.1 log units (2 dB) for Observer M1, and ±0.05 log units (1 dB) for Observers M2, M3, B2, and B3, whereas standard levels with and without flankers for Observer B1 were actually identical. With the necessary precautions in the interpretation of these results, the bottom row of Fig. 7a plots PSEs, discrimination thresholds, and support of psychometric functions with and without flankers against one another, with solid symbols for Observer M1 (for whom standard levels with and without flankers differed by 0.1 log units), open symbols for Observer B1 (for whom standard levels with and without flankers did not differ), and gray symbols for the remaining observers (for whom standard levels with and without flankers differed by ±0.05 log units). The left panel in the bottom row of Fig. 7a shows differences between PSEs with and without flankers that mostly reflect the fact that the standard levels were not always the same in either case and, thus, that solid symbols lie relatively far below the diagonal, gray symbols lie closer to the diagonal, and open symbols lie virtually on the diagonal. The center panel in the bottom row of Fig. 7a shows that discrimination thresholds are slightly higher with flankers, but this seems only the natural consequence of the lower standard levels used with flankers, which are indeed associated with higher discrimination thresholds (see the center panel in the top row of Fig. 7a). Finally, the right panel in the bottom row of Fig. 7a shows that support with flankers is again generally larger than without them, something that cannot be attributed to any relation between support and standard level (see the right panel in the top row of Fig. 7a). In this case, the average support with flankers was 0.742 with a standard deviation of 0.145, whereas the average support without flankers was 0.634 with a standard deviation of 0.103. The difference is significant by the Bradley–Blackwood test, F(2, 34) = 16.485, p < .0001.

Fig. 7

a Variations in PSE, discrimination threshold, and support of the psychometric functions for discrimination as a function of standard contrast at levels near detection threshold (top row) and relation between PSE, discrimination threshold, and support with and without flankers at the same standard levels (bottom row). Data from different observers are represented with different symbols. In the top row, open symbols denote results without flankers and solid symbols denote results with them; in the bottom row, open symbols denote results in which the standard levels with and without flankers were identical, gray symbols denote results in which the standard levels with and without flankers differed by ±0.05 log units, and solid symbols denote results in which the standard levels with and without flankers differed by 0.10 log units. b Relation between PSE, discrimination threshold, and support with and without flankers at standard levels above detection threshold. Data from different observers are represented with different symbols

In sum, at standard levels near the detection threshold, the support of psychometric functions for discrimination seems slightly larger in the presence of flankers. There are also clear and significant traces that discrimination thresholds decrease as the level of the standard stimulus increases (center panel in the top row of Fig. 7a), whether with or without flankers, although no such relation appears to exist in either case in terms of the support of the underlying psychometric functions (right panel in the top row of Fig. 7a).

Figure 7b shows the relationship between psychometric functions for discrimination with and without flankers at standard levels well above the detection threshold. Since the set of levels used with and without flankers was the same for each observer (see Table 1), data plotted in the panels of Fig. 7b can be subjected to thorough statistical analyses. Figure 7b shows that, whether with or without flankers, the PSE is approximately at the same location (left panel), the discrimination threshold is also similar (center panel), and the support of the underlying psychometric functions is also similar (right panel). Furthermore, the center and right panels in Fig. 7b look about the same, a consequence of the fact that discrimination thresholds are more accurate indices of the support of the underlying functions in the absence of large differences between the upper and lower asymptotes of the psychometric function. Across the board, Bradley–Blackwood tests revealed nonsignificant differences only in the case of the PSEs in the left panel of Fig. 7b, F(2, 34) = 0.007, p = .9925. Concerning the center panel of Fig. 7b, the average discrimination threshold with flankers was 0.098 with a standard deviation of 0.027, whereas the average discrimination threshold without flankers was 0.089 with a standard deviation of 0.018— differences that were nevertheless significant, mostly as a result of the quite divergent variances, F(2, 34) = 7.016, p = .0028. Similarly, in the right panel of Fig. 7b, the average support with flankers was 0.802 with a standard deviation of 0.223, whereas the average support without flankers was 0.734 with a standard deviation of 0.143, differences that were also significant for the same reason, F(2. 34) = 7.290, p = .0023. Thus, the larger support of the psychometric function for detection in the presence of flankers (with a difference of about 0.13 units; see the center panels in Fig. 5a, b) persisted to a slightly lesser extent (about 0.11 units) at near-threshold contrast levels and was further reduced to about 0.07 units (although the difference was still significant) at contrast levels well above the detection threshold.

Efficacy of the manipulation to eliminate order effects due to response bias

We argued in the introduction that the provision of a “don’t know” response option and application of Fechner’s (1860/1966) half right and half wrong rule eliminates order effects caused by response bias and renders psychometric functions that are not significantly displaced in opposite directions when fitted to the subset of trials in which the test was presented first versus to the subset of trials in which the test was presented second. Analyses presented in the preceding section were carried out on aggregated data from both trial types, but it is worth seeking traces of order effects. For this purpose, sets of psychometric functions were fitted as described above, but separately to data coming from the subsets of trials in which the test was presented first and to data coming from the subset of trials in which the test was presented second. The magnitude of order effects was then defined as in Alcalá-Quintana and García-Pérez (in press), namely, as the difference between the estimated PSE and the level of the standard stimulus—that is, as PSE–x _s. This difference can also be computed when the PSE is estimated from aggregated data across presentation orders, even though the name “order effect” does not make sense in such case and presumably reflects only sampling error.

The left panel of Fig. 8 plots PSE–x _s when the test is presented second, against PSE–x _s when the test is presented first. In a plot such as this, order effects show in that data points are concentrated along the negative diagonal and significantly away from the origin of coordinates. The obvious negative correlation in the left panel of Fig. 8 is significant whether for data with flankers [r = –.66; 95% confidence interval (–.80 , –.44)] or for data without them [r = –.78; 95% confidence interval (–.88 , –.63)], but the vast majority of data points actually lie around the origin of coordinates, indicative of a lack of order effects, except in a few cases. It should be noted that order effects that are exclusively caused by response bias further result in that the difference PSE–x _s from aggregated data is unrelated to the difference PSE–x _s computed either when the test is presented first or when the test is presented second, and this is a defining property of what Ulrich and Vorberg (2009) called “Type-A order effects.” Contrary to this expectation, the center panel of Fig. 8 reveals a significant positive correlation whether with flankers [r = .48; 95% confidence interval (.20 , .68)] or without them [r = .56; 95% confidence interval (.31 , .74)]. And, in the right panel, the correlation is significantly different from zero with flankers [r = .32; 95% confidence interval (.02 , .57)], but not without them [r = .06; 95% confidence interval (–.25 , .36)]. The presence of these correlations is suggestive of what Ulrich and Vorberg called “Type-B order effects,” which cannot be attributed to response bias and, hence, cannot be eliminated with our strategy. Then, thus far, Fig. 8 suggests that order effects arising from response bias have actually been eliminated, although some other unknown source of order effects still exists that has contaminated the data from a few observers in a few conditions.⁷ Interestingly, these residual Type-B order effects do not seem to have contaminated our primary estimates (namely, the support of psychometric functions), as will be discussed next.

Fig. 8

Scatterplot of the difference between the estimated PSE and the standard stimulus level (St) across psychometric functions fitted to data from trials in which the test stimulus was presented first, to data from trials in which it was presented second, or to aggregated data from both presentation orders. Open symbols denote conditions without flankers; solid symbols denote conditions with them. Data from different observers are plotted with different types of symbols. Only data at the higher standard levels (at and above s ₆) are included in this analysis, because the lower asymptote of the remaining data sets is much too high (see Fig. 6)

The left panel of Fig. 9 shows that, with flankers, estimates of support when the test is presented second (average of 0.699 with a standard deviation of 0.222) are somewhat smaller than when the test is presented first (average of 0.830 with a standard deviation of 0.280), and the difference is significant, F(2, 40)  =  9.263, p  =  .0005. The same was true and in the same direction without flankers [averages of 0.654 and 0.730, with standard deviations of 0.156 and 0.162; F(2, 40)  =  6.373; p  =  .0040]. This is the defining property of Type-B order effects which, in principle, have the drawback that the support of the psychometric function (and, in turn, the discrimination threshold) varies with presentation order and, in consequence, may potentially inflate estimates of support (or discrimination threshold) obtained from aggregated data (García-Pérez & Alcalá-Quintana, 2010a). Interestingly, this inflation has not occurred here, as the center and right panels of Fig. 8 reveal: Estimates of support from aggregated data are similar to estimates obtained from the subset of trials in which the test was presented first (center panel in Fig. 9), although they are necessarily larger than estimates obtained from the subset of trials in which the test was presented second (right panel of Fig. 9). In the presence of Type-B order effects—and the ensuing uncertainty as to whether the actual support (or discrimination threshold) is that estimated when the test is presented first or second—one can only hope that support estimates from aggregated data are not further contaminated by this characteristic and that they are not still larger than estimates obtained from the least favorable presentation order. This is actually the case here: From the center panel in Fig. 9, average support from aggregated data is 0.806 (SD: 0.210) with flankers and 0.731 (SD: 0.141) without them, figures that compare well with those of estimates coming from trials in which the test was presented first (averages of 0.830 and 0.730, respectively, already reported in the discussion of the left panel of Fig. 9). The Bradley–Blackwood test came out significant only with flankers and only because the standard deviations differed meaningfully; a more relevant (for our present purpose) paired-samples t test revealed that the average support is not significantly different between the two conditions whether with flankers or without them.

Fig. 9

Scatterplot of estimated support across psychometric functions fitted to data from trials in which the test stimulus was presented first, to data from trials in which it was presented second, or to aggregated data from both presentation orders. Open symbols denote conditions without flankers; solid symbols denote conditions with them. Data from different observers are plotted with different types of symbols. Only data at the higher standard levels (at and above s ₆) are included in this analysis, because the lower asymptote of the remaining data sets is much too high (see Fig. 6)

In sum, Type-A order effects caused by response bias appeared to be eliminated by application of the half right and half wrong method, but traces of Type-B order effects are visible in our data whose cause is unknown. Nevertheless, estimates of support obtained from aggregated data do not seem to be inflated by these Type-B order effects.

Estimated TvC curves

Figure 7 suggests that psychometric functions for discrimination do not differ meaningfully with and without flankers. No other study that we know of has measured psychometric functions in these conditions, but discrimination thresholds obtained with adaptive procedures have been used to determine TvC curves (Adini & Sagi, 2001; Chen & Tyler, 2001, 2002, 2008; Zenger-Landolt & Koch, 2001). We thus plotted our results also in this form, as shown by the symbols in Fig. 10. In the aforementioned studies, empirical TvC data were used to fit models involving a particular transducer function. Here, we fitted the typical transducer function

$$ \mu (c) = \frac{{{{\left( {c{S_E}} \right)}^P}}}{{{{\left( {c{S_I}} \right)}^q} + Z}} $$

(6)

to our raw data (i.e., to the entire set of data displayed in our Figs. 4a and 6, not just to the summaries plotted in Fig. 10) separately for each observer and condition. Equation 6 is the well-known transducer function proposed by Foley (1994) and further described by Foley and Schwarz (1998), which assumes that responses are based on excitatory (represented in the numerator) and inhibitory (represented in the denominator) influences; for additional details regarding the parameters of Equation 6, see also García-Pérez and Alcalá-Quintana (2007b). We fitted separate transducer functions for the conditions with and without flankers because our only aim was to obtain an accurate closed-form summary of empirical data in each case, rather than to test particular hypotheses or fit particular models. The functions were fitted as described in García-Pérez and Alcalá-Quintana (2007b) and, as usual, parameter S _E was set equal to 100 to fix the scale for the remaining (free) parameters. The resultant parameter estimates are given in Table 2.

Fig. 10

TvC function for each observer. Open symbols and dashed curves reflect results without flankers; solid symbols and curves reflect results with flankers. Data points indicate the log increment contrast ${ \log }\left( {\Delta c} \right) = { \log }\left( {10^{{x_{{75}}}} - 10^{{x_{{50}}}}} \right)$, where x ₇₅ is the target contrast required to attain a discrimination performance level π_T = .75, and x ₅₀ is the PSE, plotted as a function of the standard contrast x _s. Points plotted outside the frame on the left of each panel represent detection thresholds at π_T = .75. Dashed and solid lines (for conditions without and with flankers, respectively) are predicted TvC curves from Equation 6 with maximum-likelihood estimates of its parameters

Table 2 Maximum-likelihood estimates of the parameters of the transducer function in Equation 6 for each observer and condition

The transducer functions thus fitted actually generate predicted psychometric functions for detection and for discrimination at any standard level (see García-Pérez & Alcalá-Quintana, 2007b). Then, the 75% and the 50% points x ₅₀ and x ₇₅ on each of these predicted functions were determined, and the increment threshold $\Delta c = 10^{{x_{{75}}}} - 10^{{x_{{50}}}}$ was plotted as a function of standard contrast x _s, yielding the dashed (for the condition without flankers) and solid (for the condition with flankers) curves in the panels of Fig. 10. In general, TvC curves with and without flankers only differed either at the low-contrast region (Observers M1 and B2) or as to the depth of the dipper (Observers M2, M3, and B1); they did not differ in any meaningful respect for Observer B3, and only for Observer M2 was a difference observed in the high-contrast region. Also, no consistent pattern of variation across observers could be appreciated.

Discussion

We have measured psychometric functions for detection and discrimination with and without flankers, and our results confirm again that psychometric functions for detection are flatter in the presence of flankers. Our results also show that a flattening of the psychometric functions for discrimination is mildly present near the detection threshold, but that it virtually disappears well above the detection threshold. At the same time, detection thresholds are generally lower in the presence of flankers, but (with the exception of Observer M2) discrimination thresholds generally remain the same whether flankers are or are not present. Finally, our results corroborate a feature that was also reported in earlier studies, namely, the heterogeneity of flanker effects across observers.

Comparison with previous results

The TvC data and curves in our Fig. 10 reveal a new type of pattern as compared with two other patterns that have been described in the literature (see Adini & Sagi, 2001; Chen & Tyler, 2001, 2002, 2008; Zenger-Landolt & Koch, 2001) and that were also mentioned in the introduction. In comparison, our data show instead little differences between TvC curves with and without flankers. This lack of major differences in TvC curves was accompanied by a lack of major differences in the support of the psychometric functions for discrimination with and without flankers at high standard levels—a characteristic that cannot be contrasted against previous results because those studies measured only discrimination thresholds.

How, then, can these three patterns of results be reconciled? It could certainly be that the discrimination thresholds measured in other studies were contaminated by order effects (one of whose sources was eliminated by our method) and that the unknown source of these order effects differentially affects conditions with flankers and without them. But, at the same time, the three patterns have each been obtained with a different psychophysical procedure: adaptive threshold estimation using up–down staircases (Adini & Sagi, 2001; Zenger-Landolt & Koch, 2001), adaptive threshold estimation using Bayesian methods (Chen & Tyler, 2001, 2002, 2008), and estimation of psychometric functions with elimination of order effects caused by response bias (the present study).

Zenger-Landolt and Koch (2001) and Adini and Sagi (2001) both obtained similar patterns by using up–down staircases with equal sizes for the steps up and down, which they claimed to converge on the 79.3%-correct (or 79%-correct) point on the psychometric function. It has been shown, however, that these staircases do not converge on their presumed points and that use of steps up and down of the same size make their convergence point highly dependent on both the starting point of the staircase and the relative size of the steps with respect to the support of the psychometric function (Faes et al., 2007; García-Pérez, 1998, 2000). Furthermore, these staircases were designed for use in 2AFC detection tasks in which the psychometric function has a lower asymptote at .5; 2AFC discrimination tasks with high-contrast standards render instead psychometric functions with a lower asymptote near zero (see Fig. 3), thus similar to those that apply in yes–no tasks and for which staircases set up as those in the studies of Zenger-Landolt and Koch and Adini and Sagi have an even more erratic behavior (García-Pérez, 2001). Thus, each of the data points estimated by Zenger-Landolt and Koch or Adini and Sagi for their TvC curves actually reflects a distinctly different (and largely unknown) percentage-correct level, and variations in this particular level across the board may actually be very large owing to variations in the support and lower asymptote of the underlying psychometric functions. Neither Zenger-Landolt and Koch nor Adini and Sagi measured psychometric functions and, therefore, it is uncertain how large the effect may be, but for reference, we have plotted in Fig. 11 the estimated support of the psychometric function of each of our observers in each condition (with and without flankers) as a function of standard level. This plot shows that support may vary by as much as a factor of three. At the same time, our Fig. 6 showed large variations in the lower asymptote of psychometric functions for discrimination at near-threshold standard levels along with lower asymptotes at or near zero in psychometric functions for discrimination at above-threshold contrast levels. It is therefore uncertain what it is that discrimination thresholds measured by Zenger-Landolt and Koch or Adini and Sagi actually represent. And, it should be remembered that they were also obtained under the assumption that the PSE lies exactly at the standard level (i.e., no sampling error) and under the potential contamination of order effects.

Fig. 11

Support of the psychometric functions for each observer, as a function of standard contrast. The support of the psychometric function for detection is plotted at an abscissa of -∞. Open symbols pertain to the condition without flankers; solid symbols to the condition with flankers

We should also stress that the discrepant results can hardly be attributed to other differences between our study and that of Zenger-Landolt and Koch (2001). For instance, according to results presented in García-Pérez et al. (2005), our temporal 2AFC paradigm should have increased (rather than decreased) the magnitude of facilitation found by Zenger-Landolt and Koch using a spatial 2AFC paradigm. Also, according to results presented in Giorgi et al. (2004), our foveal viewing should have increased (rather than decreased) the magnitude of facilitation found by Zenger-Landolt and Koch using eccentric viewing.

Chen and Tyler (2001), on the other hand, used quest (Watson & Pelli, 1983) to measure detection and discrimination thresholds defined as the 91.5%-correct point on the underlying psychometric functions (which they did not estimate independently either), also on the assumption that the PSE lies exactly at the standard level and without measures to prevent order effects. With small numbers of trials, this method has been shown to provide estimates that are biased toward starting point and that are also affected by large systematic errors if the actual psychometric function differs from that assumed by quest, regardless of whether the discrepancy bears upon the mathematical form of the functions, their support, or their lower and upper asymptotes (Alcalá-Quintana & García-Pérez, 2004).⁸ It has also been shown that the dependability of estimates obtained with quest and its variants is compromised when used to estimate thresholds away from the 80%-correct point on the psychometric function for detection or from the 50% point on the psychometric function for discrimination (García-Pérez & Alcalá-Quintana, 2007a). Subsequently, Chen and Tyler (2002, 2008) used a variant of quest that was designed for concurrent estimation of threshold and slope (Kontsevich & Tyler, 1999). This procedure involves a larger number of assumptions than quest, and its configuration also requires decisions that were not described by Chen and Tyler (2002, 2008), except for the fact that the procedure was set up to estimate the 75%-correct point using 40 trials. In any case, this variant of quest was also designed (and partially tested) for use in cases in which the psychometric function has a lower asymptote at .5 (i.e., for 2AFC detection tasks) and its properties, when used with discrimination tasks in which the lower asymptote of the psychometric function lies at a lower and undetermined level, are actually unknown. At the same time, results reported by Kontsevich and Tyler (1999; see their Fig. 1b) indicate that threshold estimates obtained with their method are actually positively or negatively biased to an extent that varies with the actual slope of the psychometric function (an issue that is most relevant in the present context), and that this bias is not eliminated unless more than 100 trials are administered.

In contrast, we have estimated psychometric functions for detection and discrimination, so that their support can be measured instead of inferred from discrimination thresholds. Our estimates of psychometric functions were obtained using a sampling plan whose performance has been extensively studied (García-Pérez & Alcalá-Quintana, 2005), and its setup was tailored to the characteristics of the psychometric functions at each standard level (including the case of detection, which implies a null standard) so as to maximize estimation accuracy. In addition, we allowed a “don’t know” option and we applied Fechner’s (1860/1966) half right and half wrong rule in order to eliminate spurious inflation of support due to Type-A order effects. Our results thus showed that the effect of flankers is different at contrast levels around the detection threshold (where they flatten psychometric functions) and at contrast levels well above the detection threshold (where they only seem to have a minimal effect on the support of the psychometric function and, hence, on discrimination thresholds).

Models of flanker facilitation effects

The way in which psychometric functions with and without flankers vary along the contrast continuum must constrain models of the flanker facilitation effect. In this section, we discuss whether or not the most prevalent models for the flanker facilitation effect can accommodate variations of one or another type in the support of psychometric functions.

Petrov et al. (2006) claimed that flanker facilitation is caused by uncertainty reduction. Their modeling consisted only of fitting psychometric functions for detection with and without flankers with an approach that estimates the number M of detectors that are presumably monitored by the observer during the task. The larger the number of detectors that have to be monitored, the larger the uncertainty. It has also been shown that, under this model, if the number of detectors decreases, then the psychometric function flattens (Pelli, 1985), although the reverse is not necessarily true. Given that this is an inherent property of the model, a mere visual comparison of the support of two psychometric functions would suffice to assert which case putatively involved more detectors. This model can then accommodate any observed pattern of changes in the support of psychometric functions with and without flankers, and will attribute these changes to variations in the number of receptors that are involved, with no more supporting evidence than the estimated number of receptors provided by the fit. Petrov et al. argued that this uncertainty reduction occurs because flankers indicate the location of the target. If this were the actual cause of flanker facilitation, a similar reduction should be observed if uncertainty about the location of the target were eliminated in some other way. For instance, in our foveal conditions with fixation markers, there is no more uncertainty about the location of the target without flankers than with them, and yet, our data indicate that detection thresholds in these conditions are still generally lower in the presence of flankers. The same results were observed in other studies that used foveal presentations with fixation aids. It seems, then, that uncertainty reduction is not a tenable explanation (besides not being supported by any other evidence than an intrinsic property of a model). A similar argument against uncertainty reduction has been elaborated by Chen and Tyler (2008). Morgan and Dresp (1995), Williams and Hess (1998), Huang and Hess (2007), Huang, Mullen, and Hess (2007), Summers and Meese (2009), Meese and Baker (2009), and Wu and Chen (2010) also presented data that prompted them to rule out uncertainty reduction as the cause of flanker facilitation.

Conventional psychophysical modeling of the flanker facilitation effect has estimated contrast response (transducer) functions from TvC data with and without flankers. This has been done under the assumption that flankers have a multiplicative effect on contrast (Chen & Tyler, 2001, 2002, 2008), under the assumption that flankers have additive and multiplicative effects at different contrast levels (Zenger-Landolt & Koch, 2001), or avoiding assumptions of this type by independently fitting separate transducer functions for the conditions with and without flankers (as was done in the present study). The effects of flankers are thus expressed directly as an alteration of the contrast response function in line with the results of physiological studies (Polat, 1999). At the same time, the variance of sensory effects with flankers or without them has been assumed to be independent of stimulus levels (i.e., the additive noise assumption). Under this approach to modeling flanker effects, the data and fitted psychometric functions in our Figs. 4a and 6 or the derived TvC data and fitted TvC curves in our Fig. 10 could be used to estimate transducer functions with and without flankers and to interpret the results along these lines, but this approach suffers from a problem that we will describe and illustrate next.

The validity of any conclusion regarding flanker-contingent changes in the transducer function rests in turn on the validity of the additive noise assumption under which the transducer functions are estimated. But it might instead be that the presence of flankers affects the variance of sensory effects (i.e., the multiplicative noise assumption, not to be confused with multiplicative effects on contrast such as those discussed in the preceding paragraph, which affect the contrast response function without altering the type of noise), whether altering also the transducer function or leaving it intact. Unfortunately, current psychophysical paradigms do not allow the determination of whether noise is additive or multiplicative: García-Pérez and Alcalá-Quintana (2009; see also Katkov, Tsodyks, & Sagi, 2006a, 2006b) have shown that empirical TvC curves can be accounted for equally accurately by a conveniently chosen transducer function coupled with additive noise or by an alternative transducer function coupled with multiplicative noise. Next, we will demonstrate this interchangeability, since this is useful in a discussion of the flanker facilitation effect.

Given that with our data the estimated TvC functions with and without flankers do not differ much (see Fig. 10), we will consider instead the data reported by Chen and Tyler (2001), which show larger differences and thus allow a clearer illustration of our point. But this illustration requires a brief description of Chen and Tyler’s (2001) method. The transducer functions fitted by Chen and Tyler (2001) had the form

$$ \mu (c) = \frac{{{K_e}{{\left( {c{S_e}} \right)}^p}}}{{{K_{{i}}}{{\left( {c{S_{{i}}}} \right)}^q} + \sigma }}, $$

(7)

and note that parameter σ in Equation 7 is not the same as the parameter that was defined in Equation 2 as a measure of the support of a psychometric function. Under their parameter-estimation approach, the transducer function for the condition without flankers was constrained to have K _e = K _i = 1, whereas that for the condition with flankers was unconstrained in this respect. In addition, the two functions were jointly fitted to the two data sets (with and without flankers) so that the remaining parameters (S _e , S _i , p, q, and σ) had the same estimated values in both functions. In other words, and given the role of parameters K _e and K _i in Equation 7, the strategy of Chen and Tyler (2001) fits a model that embeds the assumption that flankers have a multiplicative effect on contrast, whereas noise is additive. In any case, these response functions express the average sensory effect of (or the internal response to) a target as a function of contrast and, under the standard difference model with normally distributed sensory effects and fixed variance, the probability of a correct response in a 2AFC task is given by ⁹

$$ \Psi (x) = \int_0 {^{\rm{\infty}}{{\varphi }}\left( {d;{{\mu }}\left( {{{10}^x}} \right) - {{\mu }}\left( {10^{x_s}} \right),\nu } \right){\hbox{d}}\;d} = \Phi \left( {\frac{{{{\mu }}\left( {{{10}^x}} \right) - {{\mu }}\left( {10^{x_s}} \right)}}{{\sqrt {\nu } }}} \right) $$

(8)

(see García-Pérez & Alcalá-Quintana, 2007b), where φ(d; m, v) is the probability density of a normally distributed random variable D with mean m and variance v, and Φ is the unit-normal distribution function. Chen and Tyler (2001) estimated thresholds as the 91.5% point on psychometric functions and further assumed that threshold is reached when ${{\mu }}\left( {{{10}^x}} \right) - {{\mu }}\left( {10^{x_s}} \right) = 1$. Taken together, these two assumptions require $\sqrt {\hbox{v}} = 0.728755$ in Equation 8 to satisfy the definition that, at threshold, $\Psi (x) = \Phi \left( {1/0.728755} \right) = .915$. Chen and Tyler (2001) thus sought functions μ₁ (for the case without flankers) and μ₂ (for the case with flankers) such that the families of psychometric functions generated by Equation 8, that is, $\Phi \left( {\frac{{{{{\mu }}_{{1}}}\left( {{{10}^x}} \right) - {{{\mu }}_{{1}}}\left( {10^{x_s}} \right)}}{{0.728755}}} \right)$ and $\Phi \left( {\frac{{{{{\mu }}_2}\left( {{{10}^x}} \right) - {{{\mu }}_2}\left( {10^{x_s}} \right)}}{{0.728755}}} \right)$, give a satisfactory account of their empirical TvC data. This strategy assumes that flankers alter only the transducer function.

Chen and Tyler (2001) and others (Chen & Tyler, 2002, 2008; Yu, Klein, & Levi, 2002, 2003; Zenger-Landolt & Koch, 2001) actually succeeded in accounting for empirical data in this way, but the question arises as to whether the data could also be accounted for by a model in which flankers leave the transducer function intact and alter the variance of the noise. If this is the case, the success at fitting one or the other type of model would not reveal anything about the mechanism of flanker facilitation. Testing the feasibility of the alternative model implies determining whether a transducer model with multiplicative noise (i.e., one in which the variance of sensory effects changes with stimulus level according to some variance function v) can be found for data with flankers such that

$$ \Phi \left( {\frac{{{{{\mu }}_1}\left( {{{10}^x}} \right) - {{{\mu }}_1}\left( {10^{x_s}} \right)}}{{\sqrt {{\nu (x) + \nu \left( {{x_s}} \right)}} }}} \right) = \Phi \left( {\frac{{{{{\mu }}_2}\left( {{{10}^x}} \right) - {{{\mu }}_2}\left( {10^{x_s}} \right)}}{{0.728755}}} \right), $$

(9)

where the right-hand side is the family of psychometric functions generated by the additive noise model with the response function μ₂ originally fitted to data with flankers by Chen and Tyler (2001), and the left-hand side is the family of functions generated by an alternative version of the transducer model in which the response function is still μ₁ (i.e., the same one that was fitted to data without flankers) but variance is no longer constant. Clearly, such a model must exist, and its variance function v can be obtained given the necessary equality of the arguments of Φ on either side of Equation 9, first yielding

$$ \sqrt {{{{v}}\left( {{x}} \right) + {\hbox{v}}\left( {{{{x}}_{{s}}}} \right)}} = 0.728755\frac{{{{{\mu }}_{{1}}}\left( {{{10}^x}} \right) - {{{\mu }}_{{1}}}\left( {10^{x_s}} \right)}}{{{{{\mu }}_{{2}}}\left( {{{10}^x}} \right) - {{{\mu }}_{{2}}}\left( {10^x{_s}} \right)}}. $$

(10)

Finding a closed-form expression for v in Equation 10 takes some doing and may not always be possible, but this is immaterial: The TvC data of Chen and Tyler (2001), or any other data, can be accounted for on the assumption that flankers affect the variance of noise while leaving the response function unchanged. For illustration purposes, an approximation to the form of the variance function v can easily be obtained by noting that Equation 10 must also hold when x _s is the null stimulus, so that $10^{ {{x}}_{\rm{s}} } = 0$, ${{{\mu }}_1}\left( {10^{\rm{x_{\rm{s}} }}} \right) = {{{\mu }}_2}\left( {10^{\rm{x_{\rm{s}} }}} \right) = 0$, and v(x _s ) = v ₀, yielding

$$ v(x) = \left( {0.728755\frac{{{{\mu }_1}\left( {{{10}^x}} \right)}}{{{{\mu }_2}\left( {{{10}^x}} \right)}}} \right)^2 - {v_0}, $$

(11)

where v ₀ is a free parameter. Then, the variance function in Equation 11 coupled with the transducer function μ₁ will produce the same psychometric function for detection in the presence of flankers as the additive noise model of Chen and Tyler (2001) with the transducer function μ₂, and it will produce slightly different psychometric functions for discrimination owing to the fact that Equation 11 is only an approximation to the variance function that will satisfy Equation 10.

Figure 12 shows the outcomes of the multiplicative noise model for data with flankers in comparison with the original additive noise model considered by Chen and Tyler (2001). The first column shows the fitted transducer functions μ₁ and μ₂ for each observer, redrawn from Chen and Tyler’s (2001) Fig. 5. The second column shows the (constant) variance function that was implied in Chen and Tyler’s (2001) additive noise model and also shows the nonconstant variance functions that arise from Equation 11 with v ₀ = 0.15 for Observer C.-C.C., and v ₀ = 0.06 for Observer M.D.L. The third column shows the fit of the additive noise model of Chen and Tyler, redrawn from their Fig. 4, but reverses the assignment of symbol and line styles in accordance with conventions in the present article. The fourth column shows the fit of the alternative model for data with flankers in which the transducer function is the same that holds without flankers, but the variance function implies multiplicative noise (continuous curves; the dashed curves are unchanged with respect to those in the third column). Despite the gross approximation that Equation 11 represents, the fit of this multiplicative noise model for flanker effects is no worse than that of the additive noise model considered by Chen and Tyler (2001), which shows that the question as to what is it that flankers alter is very slippery. Success at fitting some model to data does not actually disclose the cause of the phenomenon. We have chosen to leave the data without flankers accounted for by the additive noise model of Chen and Tyler (2001) and to fit the data with flankers with a multiplicative noise model, but Equations 9– 11 make clear that we would also have succeeded at ascribing additive noise and multiplicative noise models in reverse.

Fig. 12

First column: Response function estimated for each of the two observers (rows) in the study of Chen and Tyler (2001) in the conditions with flankers (solid curve) and without them (dashed curve). These curves are redrawn from Fig. 5 in Chen and Tyler but are done so using line styles consistent with the conventions in the present article. Second column: Alternative variance functions representing additive noise (horizontal line) and multiplicative noise (asymptotically increasing curve); the latter was obtained through Equation 11 with v ₀ = 0.15 in the top row (Observer C.-C.C.) and v ₀ = 0.06 in the bottom row (Observer M.D.L.). Third column: Empirical TvC data from Chen and Tyler and the theoretical curves that they fitted to those data, involving different transducer functions and the assumption of equal additive noise (replotted from their Fig. 4). Fourth column: The same data as before, but now both theoretical curves arise from the same transducer function (given by the dashed curve in the left panel) in combination either with the additive noise assumption for the condition without flankers (dashed curve, which is thus identical to that plotted in the third column) or with the multiplicative noise assumption for the condition with flankers (solid curve). Note that open and solid symbols and dashed and solid curves in the two columns on the right are assigned to conditions in the opposite way to Fig. 4 in Chen and Tyler

The bottom line of the preceding demonstration is that differences in TvC data (or psychometric functions) in the absence or the presence of flankers do not by themselves reveal anything about whether response functions or noise variance (or both) are affected by the presence of flankers: The data with flankers can be equally accurately accounted for by a model in which the transducer function varies, whereas the variance function remains the same (the choice of Chen & Tyler, 2001 as well as that of all others who have addressed this issue; see Zenger-Landolt & Koch, 2001; Yu, Klein, & Levi, 2002, 2003) and by a model in which the transducer function is the same in the conditions with and without flankers but the variance function changes. This essential indeterminacy also shows that the leftward shift of psychometric functions with flankers that was reported by Shani and Sagi (2006; see also Petrov et al., 2006) can be caused by a reduction of noise variance rather by an additive effect of flankers on the contrast of the target.

Given the functional equivalence of additive noise and multiplicative noise models, experimental methods that could allow determining whether noise is additive or multiplicative would be needed to clarify whether flankers alter the contrast response function, the variance of the noise, or both. In any case, flankers seem to have a larger effect on the support of the psychometric function than they have on its location, particularly for detection and for discrimination near the detection threshold. The term flanker facilitation thus appears as a misnomer that places the emphasis in the small and unstable effect of flankers on thresholds while leaving out of the picture their actually larger and more consistent effect on the support of the psychometric function.

Conclusion

We measured psychometric functions for detection and discrimination with and without flankers using a robust psychophysical method. Our results confirm that psychometric functions for detection are flatter in the presence of flankers, that this flattening is mildly present in psychometric functions for discrimination near the detection threshold, and that it virtually disappears well above the detection threshold. When plotted in TvC form, our discrimination data describe a pattern that is distinctly different from two other patterns that have been reported in the literature, although the differences are reasonably attributed to the different psychophysical methods used across the studies that reported these three patterns.

Our results did not replicate the most common finding of earlier studies, namely that at high-contrast levels, discrimination thresholds with flankers are higher than those without flankers. Because our method eliminated Type-A order effects that spuriously broaden psychometric functions, one might speculate that, by comparison, what previous studies have actually shown is that flankers increase the magnitude of order effects, and thus produce spuriously higher discrimination thresholds. The origin of Type-B order effects still found in our data is unclear, although they have been reported to have different forms and magnitudes in different conditions (Ulrich & Vorberg, 2009). Although only a speculation at this point, flanker-contingent Type-B order effects do not seem untenable. Hopefully, further research designed also to eliminate Type-A order effects will clarify whether Type-B order effects in 2AFC discrimination tasks are actually larger with flankers than without them and, ideally, will also identify their causes and devise means for the elimination of their contaminating influence.

Our discussion of current models of flanker facilitation effects has questioned the validity of the hypothesis that flankers reduce uncertainty about the location of the target. Also, the widespread claim that flankers alter the contrast response function has been shown to reflect only the natural outcome of the modeler’s decision to attribute this particular role to the flankers by the arbitrary choice of fitting additive noise models to the data (and succeeding at that). We have shown that the alternative choice of fitting a multiplicative noise model also succeeds at accounting for the data equally accurately, and in this type of model, the contrast response function is the same with and without flankers, whereas the variance function differs in either case. The functional equivalence of these alternative explanations reveals that the cause of flanker effects cannot be determined until experimental procedures are devised that allow separate estimation of the contrast response and variance functions.

Appendix

This appendix discusses a generally widespread hardware problem that must have affected a number of studies that have used our same calibration and experimentation system (VisionWorks; Swift et al., 1997). We should nevertheless stress that this problem affects absolute measures of threshold and support of psychometric functions; therefore, they may be relevant in clinical studies in which observers’ absolute thresholds are compared to normative data for diagnosis. But, this problem has no consequence in studies such as ours, where the issue under consideration is the relative magnitudes of threshold and support across conditions (i.e., with and without flankers). Indeed, similar or even larger calibration problems have been described under the Modelfest project (see Ahumada & Scharff, 2007), which in that case affect comparisons of absolute measures across laboratories in which different equipment was used.

Monitor calibration protocols ensure proper gamma correction only under the same exact conditions that were used during calibration. Our calibration system uses a protocol that measures the luminance of a uniform patch centered on the image area and whose size is half the width and half the height of the image area, whereas the outer region of the image area on the monitor remains unlit. This was the only calibration option in the system until recently, and it is still the default option. Our experiments, on the other hand, are carried out using an average luminance field that covers the entire image area. García-Pérez and Peli (2001) showed that the RGB monitor used in Boston in the present experiments and a monochrome monitor very similar to the one used in Madrid respond differently to these changes in image size when it comes to ensuring gamma correction. In particular, for stimuli displayed at the center of the RGB monitor, actual luminance levels in the vicinity of the midrange (where our stimuli were placed) are about 95% of the nominal levels, which leaves contrast unaltered (see the strand of open circles in the bottom left panel of Fig. 5 in García-Pérez & Peli, 2001). However, on the monochrome monitor, actual luminance in this region is higher than nominal and is in a proportion that increases slightly nonlinearly with nominal luminance, although local variations within the narrow subranges involved in our experiments are approximately linear (see the strand of open circles in the bottom right panel of Fig. 5 in García-Pérez & Peli, 2001). To check whether the monitor used in Madrid was affected by the same problem, we carried out measurements such as those leading to Fig. 5 in García-Pérez & Peli (2001).

Figure 13 shows the relation between actual and nominal luminance (left panel) and the relation between actual and nominal contrast (right panel) that arose from these measurements. Quite apparently, the relation between actual and nominal luminance is still very approximately linear, although the slope is lower than unity. As for contrast, actual contrast is slightly higher than nominal contrast across the entire range, but the discrepancy is slightly larger at very low contrasts (i.e., at contrast near the detection thresholds reported in the upper panels of our Fig. 4a). In particular, when nominal contrast is 1% (–2 log units), actual contrast is about 0.16 log units higher. This characteristic might explain why the same person appears to have lower thresholds on the monochrome than on the RGB monitor (Observer M1 vs. Observer B1; see Fig. 4). To confirm this point, we plotted the data for Observer M1 in Fig. 4a (and fitted the psychometric functions) using the actual contrasts determined by the relation shown in the right panel of Fig. 13, instead of the nominal contrasts used in Fig. 4a. The results are shown in Fig. 14, which also replots the data for Observer B1 (the same person) from Fig. 4a for comparison. Clearly, thresholds and psychometric functions (including measures of support) for Observers M1 and B1 are much more coincidental here.

Fig. 13

Relation between actual and nominal luminance (left panel) and between actual and nominal contrast (right panel) in the monitor used in Madrid. The dashed diagonal is the identity line. Symbols denote measurements

Fig. 14

Top panel: Data and fitted psychometric functions for Observer M1 in Fig. 4a, but using actual rather than nominal contrast, transformed using the relation in the right panel of Fig. 13. Bottom panel: Data and fitted psychometric functions for Observer B1 (the same person) merely copied without change from Fig. 4a for comparison

To corroborate that the differences in absolute threshold could be attributed to the different behavior of the monitors and were not caused by some idiosyncratic characteristic of Observer M1/B1, psychometric functions for detection with and without flankers were also measured for Observer M2 on the RGB monitor in Boston a few months later, and the results showed differences of similar magnitude and sign: Detection thresholds without and with flankers were, respectively, 0.16 and 0.31 log units higher on the RGB monitor (Boston) than they were on the monochrome monitor (Madrid; data reported in Fig. 4a for Observer M2).

Note, finally, that the calibration problem just described (and corrected) affects only comparisons of absolute thresholds and supports across monitors, and not comparisons between stimuli presented on the same monitor (which is the actual topic of the research reported in the present article). For this reason, we decided against applying the (somewhat inaccurate) mapping described in the right panel of Fig. 13 to our entire data set.