On the tension between growth rate and CMB data

Abstract

We analyze the claimed tension between redshift space distorsions measurements of $f(z)\sigma _8(z)$ and the predictions of standard $\varLambda$CDM (Planck 2015 and 2018) cosmology. We consider a dataset consisting of 17 data points extending up to redshift $z=1.52$ and corrected for the Alcock-Paczynski effect. Thus, calculating the evolution of the growth factor in a wCDM cosmology, we find that the tension for the best fit parameters w, $\varOmega _m$ and $\sigma _8$ with respect to the Planck 2018 $\varLambda$CDM parameters is below $2\sigma$ in all the marginalized confidence regions.

1 Introduction

Large-scale galaxy surveys are becoming one of the most powerful tools to test the currently accepted $\varLambda$CDM model based on General Relativity. The possibility of mapping the distribution of matter in large volumes at different redshifts allows to measure the growth rate of structures as a function of time and (length) scale which is a well-defined prediction of any cosmological model.

The ability of such surveys to construct 3D maps depends crucially on the precise determination of galaxy redshifts from which radial distances to the survey objects can be inferred. The actual conversion depends, in turn, on two important effects. On one hand, peculiar velocities introduce distorsions in the redshift distribution, the so called redshift space distorsions (RSD), generating an anisotropic galaxy power spectrum. On the other, although at low redshift the Hubble law provides a straightforward relation between redshift and distances, at higher redshifts this conversion depends on the chosen fiducial cosmology. This fact lays behind the Alcock–Paczynski (AP) effect. In recent times these effects have allowed to measure the linear growth rate of structures, defined as $f=d\ln \delta _m/d\ln a$ with $\delta _m$ the linear matter density contrast with relatively good precision in a wide range of redshifts. More precisely, RSD provide a measurement of the quantity $f(z)\sigma _8(z)$, where $\sigma _8(z)$ is the normalization of the linear matter power spectrum at redshift z on scales of $8 h^{-1}$Mpc. In particular, measurements which can reach $10\%$ precision have been obtained at $z<1$ by different surveys such as 2dF [1], 6dFGRS [2], WiggleZ [3] and recently by SDSS-III BOSS [4] and VIPERS [5]. At higher redshifts two measurements have also been obtained recently by FMOS [6] and from the BOSS quasar sample [7] although with relatively lower precision.

Confrontation of $f(z)\sigma _8(z)$ measurements with standard $\varLambda$CDM cosmology predictions has lead in recent years to claims of inconsistency or tension at different statistical significance levels. Thus in [8] a lower growth rate than expected from Planck $\varLambda$CDM cosmology was identified for the first time. Later on [9, 10] a tension at the 2$\sigma$ level was claimed between the Planck data and the CFHTLenS determination of $\sigma _8$. A similar tension was found by the KiDS$+$VIKING tomographic shear analysis [11]. More recently [12] a 3$\sigma$ tension with respect to the best fit parameters of Planck 2015 was also identified in a set of 18 data points from RSD measurements of $f(z)\sigma _8(z)$. The tension could even increase up to $5\sigma$ if an extended dataset is used [13]. The extended dataset has far more data at low redshifts where the model discrimination is easier [14], however in this extended case possible correlations within data points have not been taken into account.¹ The possibility that more recent datapoints with larger errorbars compared to earlier datapoints could introduce a bias towards the expected standard Planck/$\varLambda$CDM cosmology is also discussed in [13].

In this paper, we follow a complementary approach, rather than using the extended dataset for which correlations are unknown, we will revisit the analysis of the tension from the most conservative point of view, i.e. using only independent datapoints or points whose correlations are known. Thus we consider the Gold dataset of [12] and introduce two changes in the analysis. Firstly, we include the most recent measurements from BOSS-Q [7] and on the other, we draw attention on the possible correlation between SDSS-LRG and BOSS-LOWZ points. Notice that the former are obtained from the SDSS data release DR7 with practically the same footprint as the later, obtained from DR10 and DR11, but with less galaxies. In this sense, we explore the consequences of removing the two SDSS-LRG points from the analysis. In this sense, our dataset is very similar to that consider by Planck collaboration [16]. On the other hand, we will take the best fit parameters of Planck 2018 (CMB alone) given in [16] rather than Planck 2015 used in [12]. We consider the same type of wCDM cosmologies with three free parameters $(w,\varOmega _m,\sigma _8)$ but obtain the confidence regions from the marginalized (rather than maximized) likelihoods. This enlarges the confidence regions so that the tension is found to be reduced below the $2\sigma$ level for all the parameters combinations.

2 Growth of structures and $f(z)\sigma _8(z)$

Let us consider a flat Robertson-Walker background whose metric in conformal time reads

$$\begin{aligned} ds^2 = a^2 (\eta ) \left[ - d\eta ^2 + \delta _{ij} dx^i dx^j \right] \end{aligned}$$

(1)

The evolution of matter density perturbations $\delta _m=\delta \rho _m/\rho _m$ in a general cosmological model with non-clustering dark energy and standard conservation of matter is given for sub-Hubble scales by

$$\begin{aligned} \delta _m '' + \mathcal {H} \delta _m ' - \frac{3}{2} \mathcal {H}^2 \varOmega _m(a) \delta _m = 0 \end{aligned}$$

(2)

where prime denotes derivative with respect to conformal time, $\mathcal{H}=a'/a$ and $\varOmega _m(a)=\rho _m/(\rho _m+\rho _{DE})$. In this work we will limit ourselves to wCDM cosmologies so that at late times

$$\begin{aligned} \mathcal{H}^2=H_0^2 a^2(\varOmega _m a^{-3}+(1-\varOmega _m)a^{-3(1+w)}) \end{aligned}$$

(3)

and

$$\begin{aligned} \varOmega _m(a) = \frac{\varOmega _{m}}{\varOmega _{m} + (1-\varOmega _m) \ a^{-3w}} \end{aligned}$$

(4)

The growth rate is defined as

$$\begin{aligned} f=\frac{d\ln \delta _m}{d\ln a} \end{aligned}$$

(5)

which can be approximated by $f\simeq \varOmega _m^\gamma (a)$ with $\gamma \simeq 0.55$ for wCDM models. Even though this fitting function provides accurate description for cosmologies close to $\varLambda$CDM, since we are interested in exploring a wide range of parameter space, in this work we will obtain f just by numerically solving (2) with initial conditions $\delta _m(a_i)=1$ and $\delta '(a_i)=1/a_i$ with $a_i$ well inside the matter dominated era.

The matter power spectrum corresponding to the matter density contrast in Fourier space $\delta _k(z)$ with $1+z=1/a$ is given by $P(k,z)=V\vert \delta _k(z)\vert ^2$ with V the volume. Thus the variance of the matter fluctuations on a scale R is given by

$$\begin{aligned} \sigma _R ^2(z) = \frac{1}{2\pi ^2} \int P(k',z) W_R ^2 (k') ^2 dk' \end{aligned}$$

(6)

with the window function defined as:

$$\begin{aligned} W_R(k)=\frac{3}{k^{3}R^{3}} \, [\sin (kR)-kR\cos (kR)] \end{aligned}$$

(7)

Thus $\sigma _8(z)$ corresponds to $\sigma _R(z)$ at the scale $R= 8 h^{-1}$ Mpc.

From the matter power spectrum it is possible to define the galaxy power spectrum as $P_g(k,z)=b^2(z)P(k,z)$ with b(z) the bias factor.

From the observational point of view, galaxy surveys are able to determine the galaxy power spectrum in redshift space, which is given by

$$\begin{aligned}&P_{r,\text {obs}} (k_r,\mu _r ; z) \nonumber \\&\quad =\frac{H(z) d_{Ar} ^2 (z)}{H_r (z) d_A^2 (z)} D^2 (z) b^2 (z) \left[ 1 + \beta (z) \mu ^2 \right] ^2 P(k,z=0)\nonumber \\ \end{aligned}$$

(8)

where $H(z)=(1+z)\mathcal{H}(z)$,

$$\begin{aligned} d_A (z) = \frac{1}{1+z} \int _{\frac{1}{1+z}}^1 \frac{1}{a^{1/2}} \frac{da }{H_0 \sqrt{\varOmega _{m} + (1-\varOmega _{m} ) \ a^{-3w}}} \end{aligned}$$

(9)

is the angular diameter distance, $D(z)=\delta _m(z)/\delta _m(0)$ is the growth factor, $\beta (z) = f(z)/b(z)$ and $\mu$ is the cosine of the angle between $\hat{k}$ and the observation direction. Finally, the index r denotes that the corresponding quantity is evaluated on the fiducial cosmology. Notice that the first factor in (8) corresponds to the AP effect, whereas the $(1+\beta \mu ^2)^2$ factor is generated by the RSD. As we see RSD induce an angular dependence on the power spectrum which contains a monopole, quadrupole and hexadecapole contributions. From the measurements of monopole and quadropole it is possible to obtain the $f(z)\sigma _8(z)$ function that for simplicity in the following we will simple denote $f\sigma _8(z)$. The measured value depends on the fiducial cosmology, so that in order to translate from the fiducial cosmology used by the survey to other cosmology it is needed to rescale by a factor [12]

$$\begin{aligned} \text {ratio}(z) = \frac{H(z) d_A (z)}{H_r(z) d_{A,r}(z)} \end{aligned}$$

(10)

The fiducial cosmology correction could affect not only $f\sigma _8$ but also the power spectrum or even introduce additional multipoles in the galaxy power spectrum in redshift space. In principle, all these effects could be properly taken into account but, as shown in [13], in practice an approximated approach is employed which relies on the introduction of correction factors. In our case, and in order to check the results of [12] and [13], we have chosen the same correction factors used in those references. The same factors were used in [8]. In any case, different approaches can change the significance of the tension.

3 Testing Planck cosmology

In order to confront the predictions of standard $\varLambda$CDM model with $f\sigma _8(z)$ measurements, we will obtain theoretical predictions for a general wCDM model with three free parameters $(\varOmega _m, w,\sigma _8)$ with $\sigma _8=\sigma _8(z=0)$. Our benchmark models will correspond to the Planck 2015 and Planck 2018 (TT,TE,EE+lowE) best fit parameters in Table 1.

Table 1 Planck 2015 [17] and 2018 [16] (TT,TE,EE$+$lowE) best fit $\varLambda$CDM parameters

On the other hand, our data points will correspond to measurements of SDSS [18,19,20]; 6dFGS [21]; IRAS [22, 23]; 2MASS [22, 24]; 2dFGRS [25], GAMA [26], BOSS [27], WiggleZ [28], Vipers [5], FastSound [6] and BOSS Q [7]. In Table 2 we show the 17 independent data points with the corresponding fiducial cosmology parameters corresponding to the so called Gold-2017 compilation of [12] which contains 18 robust and independent measurements based on galaxy or SNIa observations together with an additional independent BOSS quasar point. As mentioned before, we have removed the two SDSS-LRG-200 points since they are based on almost the same galaxy selection as the BOSS-LOWZ point from two heavily overlapping footprints with BOSS-LOWZ including fainter galaxies. On the data provided by these surveys we will apply the fiducial cosmology correction given by (10).

Table 2 Data points from [7, 12]

Apart from the errors quoted in Table 2, the three points corresponding to WiggleZ are correlated. Thus the non-diagonal covariance matrix for the data points 11, 12, 13 is given by:

$$\begin{aligned} C_{ij} ^{11,12,13} = 10^{-3} \left( \begin{array}{ccc} 6.4000 &{} 2.570 &{} 0.000 \\ 2.570 &{} 3.969 &{} 2.540 \\ 0.000 &{} 2.540 &{} 5.184 \end{array} \right) \end{aligned}$$

(11)

and the total covariance matrix would be

$$\begin{aligned} C_{ij} = \left( \begin{array}{cccc} \sigma _1 ^2 &{} 0 &{} 0 &{} ... \\ 0 &{}C_{ij}^{11,12,13} &{} 0 &{} ... \\ 0 &{} 0 &{} ... &{} \sigma _N^2 \end{array} \right) \end{aligned}$$

(12)

The corresponding $\chi ^2$ is defined as

$$\begin{aligned} \chi ^2(\varOmega _m,w,\sigma _8)=V^i C_{ij}^{-1} V^j \end{aligned}$$

(13)

with $V^i= f\sigma _{8,i} - \text {ratio}(z_i) f\sigma _8 (z_i; \varOmega _m,w,\sigma _8)$. Here $f\sigma _{8,i}$ corresponds to each of the data points in Table 2 and $f\sigma _8 (z_i; \varOmega _m,w,\sigma _8)$ is the theoretical value for a given set of parameters values. In order to obtain the two-dimensional confidence regions for the different pairs of parameters, we will construct the marginalized likelihoods integrating the remaining parameter with a flat prior,² i.e.

$$\begin{aligned} L(w,\sigma _8)=N\int _{\varDelta \varOmega _m} e^{-\frac{1}{2}\chi ^2(\varOmega _m,w,\sigma _8)}\,d\varOmega _m \end{aligned}$$

(14)

Fig. 1

Blue line corresponds to wCDM best fit, purple line corresponds to Planck 2015 and grey line to Planck 2018

Table 3 Values of $\chi ^2$ for the models plotted in Fig. 1. $\chi ^2_{LRG}$ refers to the dataset in [12] whereas $\chi ^2_N$ refers to the data set in this work in Table 2. The best fit parameters for wCDM with LRG data points are $\sigma _8=1.57$, $\varOmega _M=0.1$ and $w=-0.27$. The tension between Planck cosmologies and wCDM for three fitted parameters is also shown in parenthesis

Fig. 2

w vs. $\varOmega _{m}$ 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence regions. Left: maximized contours with $\sigma _8=0.812$. The Planck 2018 point lays at $1.56\sigma$. Right: marginalized contours. The blue point corresponds to Planck 2015 and lays at $1.71\sigma$; and the grey point corresponds to Planck 2018 and lays also at $1.71\sigma$

In particular for $\varOmega _{m} \in [0.05;0.9]$, $w\in [-2.5;0.5]$ and $\sigma _8\in [0.1;4.0]$. We have checked that the confidence regions remain practically unchanged if we enlarge these intervals. Notice that this is one of the main differences with respect to [12] in which the remaining parameter was fixed to the Planck cosmology value. This procedure implies the introduction of a strong prior in the likelihood (14) from CMB data. However, if we want to determine the confidence regions obtained from $f\sigma _8$ data alone, no CMB information should be included in the corresponding likelihoods which is the approach considered in this work.

Fig. 3

w vs. $\sigma _8$ 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence regions. Left: maximized contours with $\varOmega _m=0.3166$. The Planck 2018 point lays at $1.19\sigma$. Right: marginalized contours. The blue point corresponds to Planck 2015 and lays at $0.26\sigma$ and the grey point corresponds to Planck 2018 and lays at $0.33\sigma$

Fig. 4

$\sigma _8$ vs. $\varOmega _m$ 1$\sigma$, 2$\sigma$ and 3$\sigma$ confidence regions. Left: maximized contours with $w=-1$. The Planck 2018 point lays at $1.68\sigma$. Right: marginalized contours. The blue point corresponds to Planck 2015 and lays at $1.44\sigma$. The grey point corresponds to Planck 2018 and lays at $1.23\sigma$

4 Results

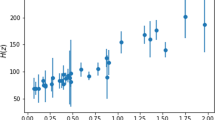
In Fig. 1, the data points quoted in Table 2 together with the corresponding wCDM best fit curve are represented. The best fit corresponds to the parameters $\varOmega _{m}=0.145$, $\sigma _8=1.18$ and $w=-0.46$. For the sake of comparison we also show the $f\sigma _8 (z)$ curves corresponding to the Planck 2015 and Planck 2018 (in Table 1) cosmologies. The $\chi ^2$ values for the different models can be found in Table 3 together with the corresponding tension level obtained from the $\chi ^2$ difference for a three-parameter distribution. As we can see, for both models the tension of Planck cosmology with respect to the best fit wCDM cosmology is below 2$\sigma$.

We see that Planck 2018 provides a better fit than the Planck 2015 cosmology, mainly thanks to the reduction in the $\sigma _8$ parameter, but still both are well above the best fit to wCDM.

In order to obtain the corresponding confidence regions we will compare two procedures. On one hand, we will follow the approach in [12] in which the likelihood is maximized, i.e. in the two-dimensional confidence regions the remaining parameter is fixed to the corresponding Planck value in Table 1. In the second procedure, the remaining parameter is marginalized as mentioned in the previous section. In Figs. 2, 3 and 4 we show the different two-dimensional confidence contours. As we can see, Planck 2018 $\varLambda$CDM shows tensions of $1.56\sigma$, $1.19\sigma$ and $1.68\sigma$ in the maximized contours which is around $1\sigma$ below the tension found in [12] with Planck 2015 parameters, partially thanks to the reduced $\sigma _8$ value of Planck 2018 as mentioned before and the exclusion of the two SDSS-LRG points. On the other hand, the marginalized contours are as expected enlarged as compared to the maximized ones. Notice also that although the form of the $(\sigma _8,w)$ and $(\varOmega _m,\sigma _8)$ contours are similar in both cases, the marginalization procedure changes the shape of the $(\varOmega _m,w)$ regions and the tensions with respect to Planck 2018 are $1.71\sigma$ for $(\varOmega _m,w)$, $0.33\sigma$ for $(\sigma _8,w)$ and in the $(\varOmega _m,\sigma _8)$ plane we get $1.23\sigma$. In Table 4 the different tension levels are summarized for the two Planck cosmologies, comparing maximized and marginalized contours and with the dataset in this work and that in [12].

5 Conclusions

We have revisited the tension of $\varLambda$CDM Planck cosmology with RSD growth data. We have considered the Gold data set of [12] together with one additional BOSS-Q point and removing the two SDSS-LRG points thus obtaining a total of 17 independent data points.

Confronting these data with the growth rate obtained from a wCDM cosmology with three independent parameters $(w,\varOmega _m,\sigma _8)$, we find that unlike previous claims, the tension with Planck 2018 cosmology is below the $2\sigma$ level in all the two-dimensional marginalized confidence regions. This reduction, which is around $1.5\sigma$ as compared to [12], is due to three different factors, namely, the use of Planck 2018 parameters, the fact that marginalized confidence regions have been considered and the exclusion of the possibly correlated SDSS-LRG points. Notice that for the $\varLambda$CDM model (i.e. fixing $w=-1$), the tension is found to be at $1.68\sigma$ level.

Future galaxy surveys such as J-PAS [29], DESI [30] or Euclid [31] with increased effective volumes will be able to reduce the error bars in the determination of $f\sigma _8(z)$ in almost an order of magnitude and will help to confirm or exclude the tension analyzed in this work.

Table 4 Tension levels for the Planck 2015 and Planck 2018 $\varLambda$CDM cosmologies in the different two-dimensional maximized and marginalized regions for the datasets in Table 2 (N) and in [12] (LRG)