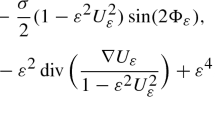Abstract
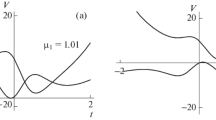
We study ferromagnetic dissipative systems described by the isotropic LLG equation, from the standpoint of their spatially localized dynamical excitations. In particular, we focus on dissipative soliton solutions of a nonlocal NLS equation to which the LLG equation is transformed and use Melnikov’s theory to prove the existence of these solutions for sufficiently small dissipation. Next, we employ pseudospectral and PINN (physics-informed neural network) numerical techniques of machine learning to demonstrate the validity of our analytic results. Such localized structures have been detected experimentally in magnetic systems and observed in nano-oscillators, while dissipative magnetic droplet solitons have also been found theoretically and experimentally.






Similar content being viewed by others
References
M. Lakshmanan, Th. W. Ruijgrok, and C. J. Thompson, “On the dynamics of continuum spin systems,” Phys. A, 84, 577–590 (1976).
L. D. Landau and E. M. Lifshitz, “On the theory of the dispersion of magnetic permeability in ferromagnetic bodies,” Phys. Z. Sowjetunion, 8, 153–164 (1935).
T. L. Gilbert, “A phenomenological theory of damping in ferromagnetic materials,” IEEE Trans. Magn., 40, 3443–3449 (2004).
D. C. Mattis, The Theory of Magnetism I: Statics and Dynamics (Springer Series in Solid-State Sciences, Vol. 17), Springer, Berlin (1988).
M. D. Stiles and J. Miltat, “Spin-transfer torque and dynamics,” in: Spin Dynamics in Confined Magnetic Structures III (Topics in Applied Physics, Vol. 101, B. Hillebrands and A. Thiaville, eds.), Springer, Berlin–Heidelberg (2006), pp. 225–308.
M. Lakshmanan, “The fascinating world of the Landau–Lifshitz–Gilbert equation: an overview,” Philos. Trans. Roy. Soc. London Ser. A, 369, 1280–1300 (2011).
O. Descalzi, M. Clerc, S. Residori, and G. Assanto (eds.), Localized States in Physics: Solitons and Patterns, Springer, Berlin–Heidelberg (2011).
Z. Ahsan and K. R. Jayaprakash, “Evolution of a primary pulse in the granular dimers mounted on a linear elastic foundation: An analytical and numerical study,” Phys. Rev. E, 94, 043001, 15 pp. (2016).
W. Królikowski, O. Bang, N. I. Nikolov, D. Neshev, J. Wyller, J. J. Rasmussen, and D. Edmundson, “Modulational instability, solitons and beam propagation in spatially nonlocal nonlinear media,” J. Opt. B: Quantum Semiclass. Opt., 6, S288–S294 (2004).
A. N. Slavin and V. S. Tiberkevich, “Spin wave mode excited by spin-polarized current in a magnetic nanocontact is a standing self-localized wave bullet,” Phys. Rev. Lett., 95, 237201, 4 pp. (2005).
M. A. Hoefer, T. J. Silva, and M. W. Keller, “Theory for a dissipative droplet soliton excited by a spin torque nanocontact,” Phys. Rev. B, 82, 054432, 14 pp. (2010).
S. M. Mohseni, S. R. Sani, J. Persson et al., “Spin torque-generated magnetic droplet solitons,” Science, 339, 1295–1298 (2013).
I. V. Barashenkov, S. R. Woodford, and E. V. Zemlyanaya, “Interactions of parametrically driven dark solitons. I. Néel–Néel and Bloch–Bloch interactions,” Phys. Rev. E, 75, 026604, 18 pp. (2007).
V. Besse, H. Leblond, D. Mihalache, and B. A. Malomed, “Pattern formation by kicked solitons in the two-dimensional Ginzburg–Landau medium with a transverse grating,” Phys. Rev. E, 87, 012916, 12 pp. (2013).
Y. Lan and Y. C. Li, “Chaotic spin dynamics of a long nanomagnet driven by a current,” Nonlinearity, 21, 2801–2823 (2008).
M. Daniel and M. Lakshmanan, “Perturbation of solitons in the classical continuum isotropic Heisenberg spin system,” Phys. A, 120, 125–152 (1983).
St. Wiggins, Introduction to Applied Nonlinear Dynamical Systems and Chaos (Texts in Applied Mathematics, Vol. 2), Springer, New York (2005).
J. Gruendler, “The existence of homoclinic orbits and the method of Melnikov for systems in \(\mathbb R^{n\,}\),” SIAM J. Math. Anal., 16, 907–931 (1985).
M. Yamashita, “Melnikov vector in higher dimensions,” Nonlinear Anal. Theory Methods Appl., 18, 657–670 (1992).
S.-N. Chow and M. Yamashita, “Geometry of the Melnikov vector,” Math. Sci. Eng., 185, 79–148 (1992).
V. M. Rothos and T. C. Bountis, “Mel’nikov analysis of phase space transport in a \(N\)-degree- of- freedom Hamiltonian system,” Nonlinear Anal. Theory Methods Appl., 30, 1365–1374 (1997).
J. Yang, Nonlinear Waves in Integrable and Nonintegrable Systems (Mathematical Modeling and Computation, Vol. 16), SIAM, Philadelphia, PA (2010).
M. Raissi, P. Perdikaris, and G. E. Karniadakis, “Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations,” J. Comput. Phys., 378, 686–707 (2019).
V. M. Rothos and A. F. Vakakis, “Dynamic interactions of traveling waves propagating in a linear chain with local essentially nonlinear attachment,” Wave Motion, 46, 174–188 (2009).
K. J. Palmer, “Exponential dichotomy and transversal homoclinic orbits,” J. Differ. Equ., 55, 225–256 (1984).
P. Tsilifis, P. G. Kevrekidis, V. M. Rothos, “Cubic-quintic long-range interactions with double well potentials,” J. Phys. A: Math. Theor., 47, 035201, 21 pp. (2014); arXiv: 1207.6731.
Funding
T. Bountis acknowledges that his work on Sections 2, 3.1 and 3.2 of this paper was supported by the Russian Science Foundation project No. 21-71-30011. T. Bountis also acknowledges partial support for Section 3.3 by the grant No. AP08856381 of the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan, for the project of the Institute of Mathematics and Mathematical Modeling MES RK, Almaty, Kazakhstan.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The authors declare no conflicts of interest.
Additional information
Prepared from an English manuscript submitted by the authors; for the Russian version, see Teoreticheskaya i Matematicheskaya Fizika, 2023, Vol. 215, pp. 190–206 https://doi.org/10.4213/tmf10404.
Appendix: Homoclinic Melnikov theory of integro-differential equations
Here, we briefly review the theory of a more general class of perturbed nonlocal dynamical systems [24], which we used in Sec. 2 to study the existence and stability of bright solitons in the nonlocal NLS (2.2).
We start by considering a perturbed \(n\)-dimensional dynamical system of the integro-differential form
We assume that the unperturbed system (A.1) (corresponding to \(\epsilon=0\)) has a hyperbolic singular point \(x_0\) and a homoclinic orbit \(\gamma\) to \(x_0\). The linear variational equation of unperturbed system (A.1) along the homoclinic orbit \(\gamma\), written in the form
We now let \(W^{\mathrm s}_0\) and \(W^{\mathrm u}_0\) denote the respective stable and unstable manifolds of the singular point \(x_0\), and define the following projections for a given \(\alpha\in\mathbb{R}\):
We now define the perturbed stable invariant manifold of the fixed point \(x_\epsilon\) as
Letting \(\eta^{\mathrm s}_2=P(\alpha)z_{0,2}\), we can prove, using the contraction mapping theorem, that system (A.8) has the unique solution
To measure the distance between the stable and unstable manifolds of the perturbed Poincaré map, it suffices to measure the separation of these manifolds in the subspace \(\operatorname{Range}(I-P(\alpha))\cap\operatorname{Range}(I-Q(\alpha))\). Let \(\mathcal D\) denote the distance between \(W^{\mathrm s}_{\mathrm{loc}}(x_{\epsilon,\mu})\) and \(W^{\mathrm u}_{\mathrm{loc}}(x_{\epsilon,\mu})\):
We consider the problem adjoint to (A.2),
We define \(\mathcal D=\epsilon M_2+O(\epsilon^2)\), where the components of the Melnikov vector \(M_2\) are given by
Thus, the conditions for the existence of transverse intersections between the stable and unstable manifolds of a Poincaré map associated with the system of integro-differential equations (A.1) can be summarized by the following theorem [24].
Theorem.
If there exist \(\alpha\), \(\nu=(\nu_1,\ldots,\nu_{m-1})\), and \(\epsilon\) such that the Melnikov vector \(M_1(\alpha,\nu)=0\) and the \(m\) vectors \(\frac{\partial M_1}{\partial\alpha},\frac{\partial M_1}{\partial\nu_1},\ldots,\frac{\partial M_1}{\partial\nu_{m-1}}\) are all nonzero at the point \((\alpha,\nu)\), then the local stable and unstable manifolds of the Poincaré map associated with system (A.1) intersect transversally. Moreover, in the case where the Melnikov vector \(M_1(\alpha,\nu)\equiv 0\), if there exist \(\alpha\), \(\nu=(\nu_1,\ldots,\nu_{m-1})\), and \(\epsilon\) such that \(M_2(\alpha,\nu)=0\) and the \(m\) vectors \(\frac{\partial M_2}{\partial\alpha},\frac{\partial M_2}{\partial\nu_1},\ldots,\frac{\partial M_2}{\partial\nu_{m-1}}\) are all nonzero at the point \((\alpha,\nu)\), then \(W^{\mathrm s}_{\mathrm{loc}}(x_\epsilon)\) and \(W^{\mathrm u}_{\mathrm{loc}}(x_\epsilon)\) intersect transversally.
We remark that the stability of bright solitons of the nonlocal NLS with cubic and quintic nonlocal terms was studied in [26] using a different approach to analyze their dynamical behavior.
Rights and permissions
About this article
Cite this article
Rothos, V.M., Mylonas, I.K. & Bountis, T. Dissipative soliton dynamics of the Landau–Lifshitz–Gilbert equation. Theor Math Phys 215, 622–635 (2023). https://doi.org/10.1134/S0040577923050033
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0040577923050033