Skip to main content
SpringerLink
Log in

Thermal Frequency Analysis of Double CNT-Reinforced Polymeric Straight Beam

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

This paper reported the modeling steps of coupled beam nanocomposite system and its fundamental frequency characteristics. The model has been derived for two straight coupled beams (made of carbon nanotube, CNT) as the continuous transitional springs, including a middle elastic layer.

Methods

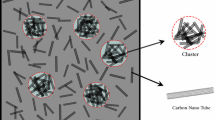
The effective properties of the beam components are evaluated based on the well-known rule of mixture. Additionally, to achieve the generality of the material distribution, various configurations of CNT have been adopted in the current model through the thickness of the structure. The main objective of the present study is to evaluate the effect of material temperature dependency on the frequency parameter of the nanocomposite double beam system. The structural model has been derived mathematically using the robust lower-order theory (first-order shear deformation, FSDT) to compute the eigenvalues without hampering the degree of solution accuracies. The nanotube properties are also considered to be temperature-dependent (TD). The final eigenvalues are computed via a semi-analytical approach, namely generalized differential quadrature (GDQ) approach.

Results

First, the natural frequencies of homogenous beam system are compared with the results of frequency parameter available in the literature. Then, the fundamental frequencies of the coupled beam system have been computed analytically for different structural input parameters (material properties, end constraints of full structure and middle elastic layer) to showcase the effect individual and/or combined conditions with and without the influence of temperature.

Conclusion

The final outcomes are revealed in detail for different input parameters and the subsequent outcomes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data Availability

The data that support the findings of this study are available from the corresponding author, upon reasonable request.

Abbreviations

\(V_{{{\text{CN}}}}^{{}}\) :

Volume of CNTs in beam

\(V_{{{\text{M}}^{^{\prime}} }}\) :

Volume of matrix in beam

\(E_{{{\text{CN}}}}^{11} \;{\text{and}}\;E_{{{\text{CN}}}}^{22}\) :

CNTs Young’s modulus

\(G_{{{\text{CN}}}}^{12}\) :

CNTs shear modulus

\(\upsilon_{{{\text{CN}}}}\) :

CNTs Poisson ratio

\(\rho_{{{\text{CN}}}}\) :

CNTs density

\(E_{{\text{M}}}^{{}}\) :

Matrix Young’s modulus

\(G_{{\text{M}}}^{{}}\) :

Matrix shear modulus

\(\upsilon_{{\text{M}}}\) :

Matrix Poisson ratio

\(\rho_{M}\) :

Matrix density

\(E_{{\text{R}}}^{11} \;{\text{and}}\;E_{{\text{R}}}^{22}\) :

Equivalent Young’s modulus

\(G_{{\text{R}}}^{12}\) :

Equivalent shear modulus

\(\upsilon\) :

Equivalent Poisson ratio

\(\rho\) :

Equivalent density

\(\eta_{1} ,\,\eta_{2} ,\,\eta_{3}\) :

Size-dependent parameters

\(D_{1}^{i} \;{\text{and}}\;D_{2}^{i}\) :

Field displacement

\(d_{1}^{i} \;{\text{and}}\;d_{2}^{i}\) :

Neutral axis displacement

\(\sigma_{x}^{i}\) :

Normal stress

\(\tau_{xz}^{i}\) :

Shear stress

\(E\) :

Elastic modulus

\(\nu\) :

Poisson’s ratio

\(N_{x}^{i}\) :

Normal force

\(Q_{x}^{i}\) :

Shear force

\(M_{x}^{i}\) :

Bending moment

\(\omega\) :

Natural frequency of system

\(\overline{\omega }\) :

Dimensionless natural frequency of system

\(D_{{{\text{eff}}}}\) :

Effective stiffness matrix

\(M_{{{\text{eff}}}}\) :

Mass matrix

\(D_{{\text{I}}}\) :

Stiffness matrix related to internal points

\(D_{{{\text{IB}}}}\) :

Internal stiffness matrix associated with BCs

\(D_{{\text{B}}}\) :

BCs matrix stiffness

\(\left\{ {X_{{\text{I}}} } \right\}\) :

Vector related to internal grid points

\(\left\{ {X_{{\text{B}}} } \right\}\) :

Vector related to BCs

K :

Stiffness of mid-layer springs

\(k_{{\text{s}}}\) :

Stiffness factor

T :

Environment temperature

\(T_{0}\) :

Room temperature (= 300° k)

References

  1. Zhao X, Chen B, Li Y, Zhu W, Nkiegaing F, Shao Y (2020) Forced vibration analysis of Timoshenko double-beam system under compressive axial load by means of Green’s functions. J Sound Vib 464:115001

    Google Scholar 

  2. Wu Y, Gao Y (2016) Dynamic response of a simply supported viscously damped double-beam system under the moving oscillator. J Sound Vib 384:194–209

    ADS  Google Scholar 

  3. Sobhani E, Masoodi AR (2021), Differential quadrature technique for frequencies of the coupled circular arch–arch beam bridge system. Mech Adv Mater Struct, pp 1–12

  4. Rezaiee-Pajand M, Rajabzadeh-Safaei N (2016) An explicit stiffness matrix for parabolic beam element. Latin Am J Solids Struct 13:1782–1801

    Google Scholar 

  5. Rezaiee-Pajand M, Mokhtari M, Masoodi AR (2018) Stability and free vibration analysis of tapered sandwich columns with functionally graded core and flexible connections. CEAS Aeronaut J 9(4):629–648

    Google Scholar 

  6. Rezaiee-Pajand M, Rajabzadeh-Safaei N, Hozhabrossadati SM (2021) On the damping influence on the dynamic analysis of functionally graded beams resting on elastic foundation by Green’s function method. Mech Based Des Struct Mach, pp 1–18

  7. Rezaiee-Pajand M, Masoodi AR (2018) Exact natural frequencies and buckling load of functionally graded material tapered beam-columns considering semi-rigid connections. J Vib Control 24(9):1787–1808

    MathSciNet  Google Scholar 

  8. Mathews P (1959) Vibrations of a beam on elastic foundation II. ZAMM-J Appl Math Mech/Zeitschrift für Angewandte Mathematik und Mechanik 39(1–2):13–19

    ADS  MathSciNet  Google Scholar 

  9. Mathews P (1958) Vibrations of a beam on elastic foundation. ZAMM-J Appl Math Mech/Zeitschrift für Angewandte Mathematik und Mechanik 38(3–4):105–115

    ADS  MathSciNet  Google Scholar 

  10. Eisenberger M (1994) Vibration frequencies for beams on variable one-and two-parameter elastic foundations. J Sound Vib 176(5):577–584

    ADS  Google Scholar 

  11. Li Z, Xu Y, Huang D (2021) Analytical solution for vibration of functionally graded beams with variable cross-sections resting on Pasternak elastic foundations. Int J Mech Sci 191:106084

    Google Scholar 

  12. Jena SK, Chakraverty S, Malikan M (2020) Vibration and buckling characteristics of nonlocal beam placed in a magnetic field embedded in Winkler-Pasternak elastic foundation using a new refined beam theory: an analytical approach. Eur Phys J Plus 135(2):1–18

    Google Scholar 

  13. Chaabane LA (2019) Analytical study of bending and free vibration responses of functionally graded beams resting on elastic foundation. Struct Eng Mech 71(2):185–196

    Google Scholar 

  14. Deng H, Cheng W, Zhao S (2017) Vibration and buckling analysis of double-functionally graded Timoshenko beam system on Winkler-Pasternak elastic foundation. Compos Struct 160:152–168

    Google Scholar 

  15. Batihan AÇ, Kadioğlu FS (2016) Vibration analysis of a cracked beam on an elastic foundation. Int J Struct Stab Dyn 16(05):1550006

    MathSciNet  Google Scholar 

  16. Shen H-S, Xiang Y (2013) Nonlinear analysis of nanotube-reinforced composite beams resting on elastic foundations in thermal environments. Eng Struct 56:698–708

    Google Scholar 

  17. Yas MH, Samadi N (2012) Free vibrations and buckling analysis of carbon nanotube-reinforced composite Timoshenko beams on elastic foundation. Int J Press Vessels Pip 98:119–128

    CAS  Google Scholar 

  18. Gibigaye M, Yabi CP, Degan G (2018) Free vibration analysis of dowelled rectangular isotropic thin plate on a Modified Vlasov soil type by using discrete singular convolution method. Appl Math Model 61:618–633

    MathSciNet  Google Scholar 

  19. Akgöz B, Mercan K, Demir Ç, Civalek Ö (2016) Static analysis of beams on elastic foundation by the method of discrete singular convolution. Int J Eng Appl Sci 8(3):67–73

    Google Scholar 

  20. Parida S, Mohanty SC (2018) Free vibration and buckling analysis of functionally graded plates resting on elastic foundation using higher order theory. Int J Struct Stab Dyn 18(04):1850049

    MathSciNet  Google Scholar 

  21. Mojiri H, Salami SJ (2022) Free vibration and dynamic transient response of functionally graded composite beams reinforced with graphene nanoplatelets (GPLs) resting on elastic foundation in thermal environment. Mech Based Des Struct Mach 50(6):1872–1892

    Google Scholar 

  22. Zhang P, Schiavone P, Qing H (2022) Stress-driven local/nonlocal mixture model for buckling and free vibration of FG sandwich Timoshenko beams resting on a nonlocal elastic foundation. Compos Struct 289:115473

    Google Scholar 

  23. Al-Shujairi M, Mollamahmutoğlu Ç (2018) Buckling and free vibration analysis of functionally graded sandwich micro-beams resting on elastic foundation by using nonlocal strain gradient theory in conjunction with higher order shear theories under thermal effect. Compos B Eng 154:292–312

    Google Scholar 

  24. Tang Y, Ding Q (2019) Nonlinear vibration analysis of a bi-directional functionally graded beam under hygro-thermal loads. Compos Struct 225:111076

    Google Scholar 

  25. Li X, Li L, Hu Y, Ding Z, Deng W (2017) Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Compos Struct 165:250–265

    Google Scholar 

  26. Abediokhchi J, Kouchakzadeh MA, Shakouri M (2013) Buckling analysis of cross-ply laminated conical panels using GDQ method. Compos B Eng 55:440–446

    Google Scholar 

  27. Tang H, Li L, Hu Y (2018) Buckling analysis of two-directionally porous beam. Aerosp Sci Technol 78:471–479

    Google Scholar 

  28. Tornabene F, Dimitri R (2018) A numerical study of the seismic response of arched and vaulted structures made of isotropic or composite materials. Eng Struct 159:332–366

    Google Scholar 

  29. Javani M, Kiani Y, Eslami MR (2021) Application of generalized differential quadrature element method to free vibration of FG-GPLRC T-shaped plates. Eng Struct 242:112510

    Google Scholar 

  30. Gholami R, Ansari R (2018) Nonlinear harmonically excited vibration of third-order shear deformable functionally graded graphene platelet-reinforced composite rectangular plates. Eng Struct 156:197–209

    Google Scholar 

  31. Shin Y-J, Kwon K-M, Yun J-H (2008) Vibration analysis of a circular arch with variable cross-section using differential transformation and generalized differential quadrature. J Sound Vib 309(1–2):9–19

    ADS  Google Scholar 

  32. Fariborz J, Batra R (2019) Free vibration of bi-directional functionally graded material circular beams using shear deformation theory employing logarithmic function of radius. Compos Struct 210:217–230

    Google Scholar 

  33. Babaei H, Kiani Y, Eslami MR (2019) Large amplitude free vibration analysis of shear deformable FGM shallow arches on nonlinear elastic foundation. Thin-Walled Struct 144:106237

    Google Scholar 

  34. Kolahi MRS, Moeinkhah H, Rahmani H (2021) Numerical study of the non-linear vibrations of electrically actuated curved micro-beams considering thermoelastic damping. Commun Nonlinear Sci Numer Simul 103:106009

    MathSciNet  Google Scholar 

  35. Dublin M, Friedrich HR (1956) Forced responses of two elastic beams interconnected by spring-damper systems. J Aeronaut Sci 23(9):824–829

    Google Scholar 

  36. Seelig J, Hoppmann W (1964) Normal mode vibrations of systems of elastically connected parallel bars. J Acoust Soc Am 36(1):93–99

    ADS  Google Scholar 

  37. Seelig J, Hoppmann I (1963) Impact on an elastically connected double beam system. Rensselaer Polytechnic Inst Troy NY

    Google Scholar 

  38. Hamada TR, Nakayama H, Hayashi K (1983) Free and forced vibrations of elastically connected double-beam systems. Bull JSME 26(221):1936–1942

    Google Scholar 

  39. Rao S (1974) Natural vibrations of systems of elastically connected Timoshenko beams. J Acoust Soc Am 55(6):1232–1237

    ADS  Google Scholar 

  40. Vu H, Ordonez A, Karnopp B (2000) Vibration of a double-beam system. J Sound Vib 229(4):807–822

    ADS  Google Scholar 

  41. Oniszczuk Z (2000) Free transverse vibrations of elastically connected simply supported double-beam complex system. J Sound Vib 232(2):387–403

    ADS  Google Scholar 

  42. Han F, Dan D, Cheng W (2018) An exact solution for dynamic analysis of a complex double-beam system. Compos Struct 193:295–305

    Google Scholar 

  43. Han F, Dan D, Cheng W (2019) Exact dynamic characteristic analysis of a double-beam system interconnected by a viscoelastic layer. Compos B Eng 163:272–281

    Google Scholar 

  44. Fei H, Danhui D, Wei C, Jubao Z (2020) A novel analysis method for damping characteristic of a type of double-beam systems with viscoelastic layer. Appl Math Model 80:911–928

    MathSciNet  Google Scholar 

  45. Pan S, Feng J, Safaei B, Qin Z, Chu F, Hui D (2022) A comparative experimental study on damping properties of epoxy nanocomposite beams reinforced with carbon nanotubes and graphene nanoplatelets. Nanotechnol Rev 11(1):1658–1669

    CAS  Google Scholar 

  46. İnada AA, Arman S, Safaei B (2022) A novel review on the efficiency of nanomaterials for solar energy storage systems. J Energy Storage 55:105661

    Google Scholar 

  47. Safaei B, Moradi-Dastjerdi R, Qin Z, Behdinan K, Chu F (2021) Determination of thermoelastic stress wave propagation in nanocomposite sandwich plates reinforced by clusters of carbon nanotubes. J Sandwich Struct Mater 23(3):884–905

    CAS  Google Scholar 

  48. Sarkon GK, Safaei B, Kenevisi MS, Arman S, Zeeshan Q (2022) State-of-the-Art review of machine learning applications in additive manufacturing; from design to manufacturing and property control. Arch Comput Methods Eng 29:1–59

    Google Scholar 

  49. Barbaros I, Yang Y, Safaei B, Yang Z, Qin Z, Asmael M (2022) State-of-the-art review of fabrication, application, and mechanical properties of functionally graded porous nanocomposite materials. Nanotechnol Rev 11(1):321–371

    CAS  Google Scholar 

  50. Mehar K, Panda SK, Mahapatra TR (2017) Thermoelastic nonlinear frequency analysis of CNT reinforced functionally graded sandwich structure. Eur J Mech-A/Solids 65:384–396

    MathSciNet  Google Scholar 

  51. Mehar K, Panda SK, Patle BK (2018) Stress, deflection, and frequency analysis of CNT reinforced graded sandwich plate under uniform and linear thermal environment: a finite element approach. Polym Compos 39(10):3792–3809

    CAS  Google Scholar 

  52. Fattahi A, Safaei B, Qin Z, Chu F (2021) Experimental studies on elastic properties of high density polyethylene-multi walled carbon nanotube nanocomposites. Steel Compos Struct 38(2):177–187

    Google Scholar 

  53. Safaei B, Onyibo EC, Hurdoganoglu D (2022) Thermal buckling and bending analysis of carbon foam beams sandwiched by composite faces under axial compression. Facta Univ Ser Mech Eng 20:589

    Google Scholar 

  54. Safaei B, Onyibo EC, Hurdoganoglu D (2022) Effect of static and harmonic loading on the honeycomb sandwich beam by using finite element method. Facta Univ Ser Mech Eng 20:279

    Google Scholar 

  55. Liu Y, Qin Z, Chu F (2021) Nonlinear forced vibrations of FGM sandwich cylindrical shells with porosities on an elastic substrate. Nonlinear Dyn 104(2):1007–1021

    Google Scholar 

  56. Qin Z, Zhao S, Pang X, Safaei B, Chu F (2020) A unified solution for vibration analysis of laminated functionally graded shallow shells reinforced by graphene with general boundary conditions. Int J Mech Sci 170:105341

    Google Scholar 

  57. Qin Z, Pang X, Safaei B, Chu F (2019) Free vibration analysis of rotating functionally graded CNT reinforced composite cylindrical shells with arbitrary boundary conditions. Compos Struct 220:847–860

    Google Scholar 

  58. Safaei B (2020) The effect of embedding a porous core on the free vibration behavior of laminated composite plates. Steel Compos Struct 35(5):659–670

    Google Scholar 

  59. Safaei B (2021) Frequency-dependent damped vibrations of multifunctional foam plates sandwiched and integrated by composite faces. Eur Phys J Plus 136(6):1–16

    MathSciNet  Google Scholar 

  60. Safaei B, Fattahi A (2017) Free vibrational response of single-layered graphene sheets embedded in an elastic matrix using different nonlocal plate models. Mechanics 23(5):678–687

    Google Scholar 

  61. Tran TT, Dinh KN, Ismail E (2022) Dynamic response of FG-CNTRC beams subjected to a moving mass. Vietnam J Sci Technol 60(5):853–868

    Google Scholar 

  62. Wang Y, Zhang Z, Chen J, Fu T (2022) Low-velocity impact response of agglomerated FG-CNTRC beams with general boundary conditions using Gram–Schmidt–Ritz method. J Braz Soc Mech Sci Eng 44(11):1–20

    CAS  Google Scholar 

  63. Cho J, Kim H (2022) Numerical optimization of CNT distribution in functionally graded CNT-reinforced composite beams. Polymers 14(20):4418

    CAS  PubMed  PubMed Central  Google Scholar 

  64. Garg A, Chalak H, Zenkour A, Belarbi M-O, Sahoo R (2022) Bending and free vibration analysis of symmetric and unsymmetric functionally graded CNT reinforced sandwich beams containing softcore. Thin-Walled Struct 170:108626

    Google Scholar 

  65. Kumar P, Kumar A (2022) Stability analysis of imperfect functionally graded CNTs reinforced curved beams. Mech Based Des Struct Mach, pp 1–22

  66. Ong OZS, Ghayesh MH, Losic D, Amabili M (2022) Coupled dynamics of double beams reinforced with bidirectional functionally graded carbon nanotubes. Eng Anal Bound Elem 143:263–282

    MathSciNet  Google Scholar 

  67. Zhao J-L, Chen X, She G-L, Jing Y, Bai R-Q, Yi J, Pu H-Y, Luo J (2022) Vibration characteristics of functionally graded carbon nanotube-reinforced composite double-beams in thermal environments. Steel Compos Struct 43(6):797–808

    Google Scholar 

  68. Shu C (1991) Generalized differential-integral quadrature and application to the simulation of incompressible viscous flows including parallel computation. University of Glasgow

    Google Scholar 

  69. Shu C (2000) Differential quadrature and its application in engineering. Springer, Berlin

    Google Scholar 

  70. Ke L-L, Yang J, Kitipornchai S (2010) Nonlinear free vibration of functionally graded carbon nanotube-reinforced composite beams. Compos Struct 92:676–683

    Google Scholar 

  71. Wu HL, Yang J, Kitipornchai S (2016) Nonlinear vibration of functionally graded carbon nanotube-reinforced composite beams with geometric imperfections. Compos B Eng 90:86–96

    CAS  Google Scholar 

Download references

Funding

This study was not funded by any company.

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Ferdowsi University of Mashhad, Mashhad, Iran

    Moein Alreza Ghandehari & Amir R. Masoodi

  2. Department of Mechanical Engineering, National Institute of Technology Rourkela, Rourkela, 769008, India

    Subrata Kumar Panda

Authors
  1. Moein Alreza Ghandehari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Amir R. Masoodi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Subrata Kumar Panda
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Amir R. Masoodi.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghandehari, M.A., Masoodi, A.R. & Panda, S.K. Thermal Frequency Analysis of Double CNT-Reinforced Polymeric Straight Beam. J. Vib. Eng. Technol. 12, 649–665 (2024). https://doi.org/10.1007/s42417-023-00865-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-023-00865-0

Keywords

Search

Navigation