Introduction

The initiation of explosives by rapid compression for the purposes of impact hazard assessment is usually performed in a falling-weight instrument. Sentencing, that is act of judging the outcome of a given impact test, is a key aspect of the test. Typically, the diagnostics available are intended for the binary sentencing of whether reaction did or did not occur, such as a report detected by a microphone [1], or the collection of product gases from chemical decomposition [2], and sometimes without even those; it being left to the operator to record whether they saw ‘sparks or a flash’ [3]. In the case of diagnostic with a recordable output, such as a microphone, a reaction is judged to have occurred if the signal exceeds some predefined threshold above the noise level, in which case the sentence is usually referred to as a ‘go’. When no reaction is judged to have occurred the sentence is usually referred to as a ‘no-go’. In any given run of tests to evaluate the sensitiveness of an explosive substance, what might typically be recorded is the mass of the falling weight, the height at which it was dropped from, and whether or not a reaction occurred. A plot of impact stimulus, such as the kinetic energy of the falling weight, versus the probability of reaction is usually sigmoidal, and statistical methods may be used to determine the level of stimulus associated with a given threshold probability of reaction, often with the goal of performing as few tests as possible [4]. Such a threshold can then be used as a measure of the sensitiveness of the explosive to impact, and comparisons can be drawn with other materials in a ranking exercise.

In terms of gaining an understanding of what processes are occurring during the impact, at the Cavendish Laboratory of the University of Cambridge there is a tradition of using falling-weight instruments that provide on-axis optical access to impacted samples [5]. Since the early 1950’s such studies have given valuable insight into the formation and growth of hot-spots, but relatively little on the mechanics involved. There are a few descriptions of falling-weight instruments instrumented with strain-gauges such that one can infer something of the dynamics of the process, but reports of their use seem to be somewhat limited [6,7,8].

In terms of mechanics, there is in fact an even longer history of characterizing explosives using so-called Hopkinson pressure bars at the University of Cambridge; one of Hopkinson’s earliest uses for a pressure bar was in an attempt to measuring the detonation pressure of gun-cotton [9]. A few decades later, Taylor used a direct impact Hopkinson pressure bar to estimate the dynamic compressive mechanical properties of cordite [10]. It is in the context of the latter case that Hopkinson pressure bars are now most commonly deployed; for informing constitutive relations of deformation, and to that end they are most commonly used in conjunction with formulated explosives to characterize their intermediate to high strain-rate mechanical properties [11,12,13,14].

There are some recent reports of initiating energetic materials and studying the dynamics of the process using split Hopkinson pressure bars, though these are typically limited to the study of aluminium-polytetrafluoroethylene mixtures [15,16,17,18,19,20]. There are also a small number of reports of so-called hybrid drop weight-Hopkinson pressure bar investigations, which are essentially direct-impact experiments [21,22,23,24].

The primary purpose of the experiments described in the present study was as assessment of the feasibility of initiating explosives, in this instance granulated 1, 3, 5, 7-tetranitro-1, 3, 5, 7-tetrazoctane, 1,3,5-Trinitro-1,3,5-triazinane, and 2,2-Bis[(nitrooxy)methyl]propane-1,3-diyl dinitrate, more conveniently referred to as HMX, RDX and PETN, in a split Hopkinson pressure bar system (SHPB). We have sentenced our experiments using photodiodes to record the light emitted during reaction, and additionally taken the opportunity to append diagnostics to study the spectral nature of that light. We find that it is feasible to initiate granulated HMX, RDX and PETN in a SHPB, and that there are compelling scientific reasons for doing so. In particular, firstly, the ability to tailor the time-history of the pressure pulse that is incident on the sample; for example in principle it is feasible to generate incident pressure profiles that are nominally half-sine, top-hat, ramping, low amplitude long duration, high amplitude short duration, etc. Secondly the relatively simple nature of the instrument makes extraction of quantitative descriptions of the dynamics a tractable proposition; for example pressure-density descriptions of the compaction of the sample, knowing what fraction of the incident elastic energy is imparted to the specimen in the run-up to initiation, and measurements of the time to reaction.

Excepting for our recent optical spectroscopy focused article [25], where our use of an SHPB was mentioned in passing as a vehicle to elicit reaction, then to the best of the authors’ knowledge, this is the first report of a study on the deliberate initiation of neat HMX, RDX or PETN powders in a split Hopkinson pressure bar instrument.

Generating Gigapascal Pressures of Microsecond Duration

It is helpful to briefly review the mechanics of falling weight machines, in order to understand the characteristics of the pressure pulses they generate, and so that we may design an SHPB system capable of reproducing the required pressures and durations.

Case of a Falling-Weight Machine

In a falling-weight experiment a typical mass m, is 1 kg, the drop-height h, is of order 0.5 m, and therefore the impact speed v, is circa 3.1 m‧s−1.

Let us assume the two anvils each have a volume of 1 cubic centimetre giving a combined volume V, and let each have a length of 1 cm giving a combined length l. Let them be formed from a steel of modulus E, equal to 200 GPa and a density ρ, of 8000 kg‧m−3. The corresponding longitudinal sound-speed in the steel c0, is given by:

$${c}_{0}=\sqrt{\frac{E}{\rho }}$$
(1)

and in this example is 5000 m‧s−1.

The initial impact stress σ0, that is generated is calculable [26] and is given by:

$${\sigma }_{0}=v\sqrt{E\rho }$$
(2)

and is found to be modest, circa 125 MPa in this example.

A much higher peak pressure is subsequently generated because the anvil-sample system is of lower mechanical impedance than both the falling weight and the base that supports it. Upon impact, only compressive waves reverberate within the anvil system, and the pressure in the anvils rings-up stepwise by a factor of σ0 upon each reflection, until a peak pressure is achieved, corresponding to the instant at which the forces acting on the falling weight have brought it to rest. If we assume that the falling weight and the base that supports it are perfectly rigid, meaning that the impedance mismatches are infinite, then all of the kinetic energy of the falling weight is converted into stored elastic energy within the anvils. In which case the corresponding peak pressure σpeak is given by:

$${\sigma }_{peak}=\sqrt{\frac{2mghE}{V}}$$
(3)

and in this example gives rise to a peak pressure of 990 MPa, or circa 1 GPa.

Thereafter the momentum of the falling-weight is reversed, and the pressure in the anvils rings-down again to zero, at which instant the weight detaches from the anvil surface and the rebound is complete. The loading path in this greatly simplified example can be described as a stepwise generated half-period of a triangle wave. The duration of the impact tw, can be estimated as:

$${t}_{w}=2\frac{{\sigma }_{{\text{peak}}}}{{\sigma }_{0}}\bullet \frac{l}{{c}_{0}}$$
(4)

and in this example is circa 65 µs.

In reality, because the impedance mismatches at the anvil interfaces are not infinite, the reverberations are not total reflections, and elastic energy passes back into the weight and the supporting base, and likewise into the ground, and so is effectively lost from the system. Consequently, the peak-stress will be less than Eq. (3) suggests, entailing more internal wave reflections, and therefore of longer duration than Eq. (4) suggests.

In terms of a more realistic wave-based estimate of the impact duration, the multi-component nature of a practical system introduces further interfaces, each with their own transmission/reflection coefficients, and from the point of view of a simple mathematical description, the problem quickly becomes intractable. Instead, inroads into the problem can be made by making the observation that the long duration of the impact relative to the duration of one reverberation within the anvils permits a quasi-static, Newtonian treatment [6]. The consequence of such an approach is that the pressure pulse should take the form of a smooth half-sine of duration tN which is given as:

$${t}_{N}=\pi l\sqrt{\frac{m}{EV}}$$
(5)

and in this example is circa 100 µs.

In practice, a pressure profile reminiscent of a half-sine is usually observed, with high-frequency low-amplitude oscillations superimposed, whose origins lie in the aforementioned ring-up and ring-down wave activity.

In considering all of the above, it is worth pointing out that differing machines that use the same masses dropped from the same height, and therefore possess the same initial kinetic energy, will, if they differ in the details of their anvil arrangements, produce differing force–time histories. And even the same machine that utilizes the same energy of drop, using smaller masses dropped from greater heights, will achieve the same peak stress in the anvils, but on time scales of ever shorter duration; the mechanical power will be greater.

However, for the purposes of the current investigation, the key point is that pressures of circa 1 GPa and durations of order 100 microseconds are commensurate with the operation of a relatively normally proportioned split Hopkinson pressure bar.

Case of Split Hopkinson Pressure Bar

The mechanical pressure in a split Hopkinson pressure bar is caused by the collision of the striker bar travelling with speed v, against the end of a stationary input bar. In the simplest case the bars are formed from the same material, having the same mechanical impedance Z, which is a convenient material property given by:

$$Z=\rho {c}_{0}$$
(6)

the bars have equal cross-sectional areas, and are flat ended. In such a scenario the pressure pulse will take the form of an approximately square wave of amplitude σ and a duration τ equal to the time taken for two wave transits in the striker bar:

$$\sigma =\frac{Zv}{2}$$
(7)
$$\tau =2\frac{{l}_{{\text{striker}}}}{{c}_{0}}$$
(8)

If one were to use bars of the same steel as the anvils described in the falling weight example discussed above, then to achieve a mechanical pressure of 1 GPa would require an impact speed of circa 50 m‧s−1, and to have a duration of > 100 microseconds would require a striker bar of length > circa 25 cm. A much greater impact speed is required in the case of the SHPB than the falling weight because the peak stress is generated in a single step, rather than relying on the superposition of many such steps, as occurs when the anvils in a falling weight instrument ring up to peak pressure.

In practice, the pressure pulses that are measured are not perfectly square, but are acute trapezoids with finite rise and fall times. They also have superimposed high-frequency oscillations, but these do not have their origin in mechanical ringing; rather they are a consequence of the fact that the position at which the waves are measured is remote from the location at which they were generated, and the waves have undergone Pochhammer–Chree propagation-based dispersion [27].

Previous experiments of ours [25] investigated the single-shot time-integrated measurement of HMX deflagration optical emission in a BAM impact machine and a split Hopkinson pressure bar; a subset of the experiments reported here. The presence of greybody features in such emission allowed the temperature of the reaction to be known, which in the SHPB case was determined to be 2900 ± 200 K. That value is some 1000 K cooler than the temperature measured in the BAM-fallhammer deflagration using the same technique. In the present study a four channel pyrometer was also deployed that allowed for time-dependent temperature measurements as the deflagration reaction evolved, and served the dual purpose of detecting reaction light to sentence reaction outcomes, and providing for an independent measurement of temperature.

Experiment Design

Choice of Pressure Bar Materials

A target pressure of circa 1 GPa immediately begins to put constraints on the design of the SHPB experiments, in particular the choice of bar material. We require that the bars remain elastic; many common bar materials are immediately ruled out because the 1 GPa is in excess of their yield strengths. For this reason, we chose to use the high-performance steel alloy Maraging 350; it will remain elastic until circa 2.4 GPa.

The Maraging 350 bars of the Cavendish Laboratory used in the present study have a measured 1-D sound speed of 4,882 m‧s−1 and a specific impedance of 39,483,160 kg‧m−2‧s−1. Both the input and output bars are of each of length 450 mm. Two striker bars were used in the present study having lengths of 150 and 70 mm; the latter to reduce the mechanical energy of the experiments once it became apparent that the longer duration pulses were not required to cause reaction. Momentum traps of length greater than the striker bar were used. All bars are centreless-ground and have nominal diameters of 12.7 mm.

The striker bars were launched by a gas-gun using compressed helium, the gas-gun is more than capable of achieving the 50 m‧s−1 impact velocities that are required.

Choice of Bar Instrumentation Methods

Diagnostics for Force Measurement

Usually, our Hopkinson pressure bars are instrumented with strain gauges to monitor the elastic waves within them, the change in resistance being converted into a voltage via a potential divider circuit and recorded on an oscilloscope. A calibration process to convert the measured voltage into force is required [28]. However, it is our experience at the Cavendish Laboratory that strain-gauges will typically start to mechanically fail at particle velocities greater than circa 10 m s−1.

For this exploratory study two approaches were taken. The first approach was to deploy the non-contact optical technique of heterodyne velocimetry (HET-V), sometimes known as PhotonDoppler Velocimetry (PDV), in conjunction with Hopkinson bar techniques [29]. An advantage of such an approach is that, because the particle velocity in the bars u is measured directly and readily converted into force F, a signal-to-force calibration process is not required:

$$F=ZAu$$
(9)

where A is the cross-sectional area of the bar.

In the first instance the analysis, which looks at the frequency content of the optical signals, particle speeds are calculated in the form of a spectrogram. The data of interest is then extracted using a local-maximum peak-finding algorithm, making use of our own in-house analysis software [30], Fig. 1 illustrates this. A downside of the homodyne PDV instrument we used is that it does not have the ability to distinguish compression from tension, as it measures speed rather than velocity.

Fig. 1
figure 1

Left: spectrogram showing particle speed in the SHPB bar corresponding to a nominally 1 GPa pressure pulse. Note the deviation from a perfect top-hat due to dispersion giving rise to Pochhammer-Chree oscillations. Right: the resultant particle-speed history extracted from the spectrogram. This signal looks like a conventionally derived strain-gauge signal—but our experience is actual strain gauges do not easily withstand such extreme conditions. The pressure in the bar is found by simply multiplying the measured particle speed by the known mechanical impedance of the bar material

Full size image

The second approach was to attempt to extend the working range of the semi-conductor strain gauges (Kulite model AFP-500-090), by taking especial care to use a minimum of solder and the thinnest possible gauge connection wires; thereby minimising any parasitic mass and helping to reduce the inertial forces that are the chief cause of gauge failure. Calibration of the strain gauges was performed in conjunction with the PDV; comparing the measured strain-gauge signals with PDV derived mechanical forces.

Figure 2 shows the resultant strain-gauge circuit calibration. Usually a calibration based upon a linear approximation is sufficient, however in the case we have adopted a third order polynomial to account for the significant departures away from linearity at large forces. On the basis of the goodness of fit to the calibration data, the uncertainty in the calculated level of force for a given gauge voltage was found to be < 2%.

Fig. 2
figure 2

Strain gauge calibration curve. The forces were deduced from particle velocities measured using the PDV system and knowledge of the physical properties of the maraging steel bars. Changes in strain gauge resistance were converted to changes in voltage using a potential divider circuit. Note the positive and negative quadrants correspond to compression and tension respectively

Full size image

In terms of force measurement, the majority of the experiments with HMX were diagnosed using PDV only, and chiefly served to demonstrate that initiation was possible and practical. The majority of the RDX and PETN experiments required lower forces and it was more practical to use strain gauges; which allowed for a more sophisticated analysis of the data, since the gauges do not suffer from our PDV’s ambiguity about particle speed direction.

Diagnostics for Reaction Sentencing and Temperature Measurement

A four-channel pyrometer provided high temporal resolution of the reaction light. However it was limited in the wavelength resolution, the opposite of our previous measurements using a single-shot spectrometer [25]. A single fibre optic was used to carry light from the experiment to the pyrometer, and simply split by launching into a 1-to-4 fan-out fibre bundle, splitting the input into four roughly equal contributions. This simple approach eliminates the use of collimator-coupled beam-splitters, or equivalent [31], and in our experience leads to more light intensity reaching the detectors by virtue of having fewer components, and therefore fewer interfaces with imperfect transmission. Light from each of the four ends of the fibre bundle was launched from a kinematically mounted wavelength specific collimator, through a bandpass filter and was directed onto the sensing element of an amplified fast photodiode [ThorLabs PDA10A2], being capable of reaching the time resolution required (rise time of 2.3 ns). The bandpass filters have full-width half-maximum bandwidths of 40 nm, which we felt was a good compromise between wavelength specificity and signal-to-noise, and for these SHPB experiments were centred on 450, 500, 700 and 750 nm.

Temperatures are calculated by fitting a greybody to the four channels, on the assumption that a single greybody can be fitted, rather than detailing a continuum, and so only a single temperature is recorded. The greybody fit takes the form of the Planck distribution (Eq. 10), where the spectral radiance, Bλ, at wavelengths, λ, depend solely on temperature, T,

$${B}_{\lambda }\left(\lambda ,T\right)=\epsilon \left(\lambda ,T\right)\bullet \frac{2h{c}^{2}}{{\lambda }^{5}}\bullet \frac{1}{{e}^{\frac{hc}{\lambda {k}_{B}T}}-1} ,$$
(10)

where all the constants have their usual meanings. For simplicity, the emissivity ϵ is assumed to be constant over the spectral range of interest.

This approach will add a bias towards measuring higher temperatures, as they have a higher intensity of emission, as can be understood from the Stefan-Boltzmann law,

$$P=\underset{0}{\overset{\infty }{\int }}d\lambda \int d\Omega {B}_{\lambda }{\text{cos}}\left(\theta \right)=\sigma {T}^{4}$$
(11)

where σ is a constant, so the emitted power, P, over all wavelengths and angles, is dependent on the fourth power of temperature.

Once setup, the pyrometer was calibrated by measuring a known blackbody source; a National Physical Laboratory verified tungsten lamp at 2856 K. This approach accounts for any bias or attenuation in the equipment used; all channels are scaled by the ratio of the measured to calculated intensities at the certified temperature, and a greybody is fitted to the results. In our analysis we do consider the transmission characteristics of the bandpass filters, but in practice this yields an almost identical result to assuming that each channel acts on the centre wavelength alone.

The relationship between temperature and intensity does, theoretically, allow temperature measurement based on intensity only (a one channel pyrometer). However, such an approach suffers from being unable to distinguish between the scenarios where a rising intensity is measured because either the source is hotter, or the number of emitters are increasing. Therefore, this method was not used in the present study; as we anticipate that the number of emitters will vary as the reactions proceed.

Materials and Conditioning

The materials in this study were used in 40 mm3 quantities, the same as recommended for BAM impact tests, and were: HMX Type-B, the β-phase polymorph, having the distribution of particle sizes given in [32]. Prior to use the HMX was dried in an oven at a temperature of 110 °C for a period of 24 h. RDX was i-RDX Type II Class 5. Prior to use it was dried in an oven at a temperature of 110 °C for a period of 24 h. The PETN was sieve-cut 85 having a mean grain size of 180 µm [33]. Prior to use it was dried in an oven at a temperature of 80 °C for a period of 24 h.

Typical masses measured for each of the 40 mm3 sample volumes are given in Table 1. Using crystalline density data [34], the tapped densities are given as a fraction of their theoretical maximum. It is likely that the starting densities in the Hopkinson bar experiments were similar to these values.

Table 1 Typical masses for the measured 40 mm3 volumes and their densities based on the data given in [34]
Full size table

Sample Confinement and Loading Procedure

For convenience, and due to their long length, Hopkinson pressure bars are typically mounted horizontally; so when testing powder specimens this presents somewhat of a difficulty.

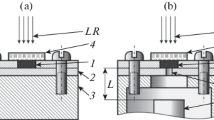
To keep the design of experiment as simple as possible, the input and output bars were used directly in contact with the specimens, without any additional anvils or end-caps. A confining sleeve was designed and made from tool steel conforming to the composition specification BS-1407. The outer diameter of the sleeve is nominally 25.0 mm, giving a nominal wall thickness of 6.15 mm. The inner diameter was bored to provide a close fit to the bars, yet still allowing a free sliding action.

Two holes were drilled into the side wall of the sleeve, one of diameter 12.7 mm to allow the sample to be loaded between the bars, and a second of diameter 2.2 mm to allow for a snug-fitted optical fibre for light detection, which is used for reaction sentencing and temperature measurement.

The procedure for loading a specimen was firstly to insert an optical fibre into the smaller port of the sleeve such that its end lay flush with the inner wall of the sleeve. Then, with the input and output bars entered into the sleeve, to fill through the large filling hole; explosive powder sat at the bottom of the cavity. The sleeve was then moved along the input bar so that the ends of the bars and the powder specimen lay between the filling and optical fibre ports. The gap between the input and output bars was closed, trapping the explosive powder in-between. Applying light pressure, and holding the input bar stationary, the output bar was given one full rotation; this action spread the powder specimen evenly over the input / output bar faces. Finally, the sleeve was slid still further down the input bar so that the fibre optic was situated directly over the sample. In this configuration, the samples were confined laterally, though not hermetically, and it is similar to the BAM impact arrangement.

Figures 3 shows photographs illustrating the experimental arrangement including a photograph of the revealed explosive layer. Upon disassembly, the sleeve and output bar came away cleanly leaving a compact of HMX on the end of the input bar. There were no obvious macroscopic defects in the compact, and the surface looked uniform.

Fig. 3
figure 3

Left: photograph of revealed HMX explosive layer sitting between the input-bar and the output-bar. The explosive layer (white) is seen through the filling port of confining sleeve. Note the smaller port to the right of the sleeve, normally used to house an optical fibre for reaction sentencing and temperature measurement. During an experiment the sleeve is slid left along the input bar so that the optical fibre is facing directly at the explosive layer. Right: upon disassembly the sleeve and output bar came cleanly away, leaving a compact of HMX on the end of the input bar. There are no obvious defects in the compact, and the surface appears uniform

Full size image

Results and Discussion

Figure 4 shows a typical result of a PETN sample reacting under the influence of a pressure pulse of nominal circa 800 MPa and 30 µs duration. The forces in the bars have been converted into a pressure in the sample by normalising with respect to the pressure bar cross-sectional areas; since the samples cover the whole of the bar end-faces. The photodiode data, the sum of amplitudes for all four channels, has been delayed by the known time taken for the elastic waves to propagate from the sample to the input/output-bar gauge positions, and indicates that reaction took place whilst the sample was under compression. It is worth noting that in the event of a ‘no-go’, when the post-impact samples were clearly unreacted, our system did not detect any light. In terms of the gauge records, we do not see any obvious evidence of the reaction in the pressure histories; neither a drop due to the sudden disappearance in load bearing capacity, nor a sudden rise due to pressurisation caused by reaction product gases. This observation is contrary to a number of instrumented drop-weight studies that report a pressure drop at the instant of reaction, notable among them being the study due to Heavens and Field [7]. However, it is worth pointing out that their experimental arrangement incorporated a recess within the sleeve surrounding the explosive layer, which would allow both for unconfined lateral expansion of both the extruded sample and the reaction product gases. Likewise, if, unlike the current experiments, the sample does not initially cover the whole of the anvils and undergoes yield or melting, then that sudden loss of strength and subsequent rapid radial flow across the anvils might also be the cause of a rapid drop in pressure [35].

Fig. 4
figure 4

A typical result of a PETN experiment subjected to a pressure pulse of circa 800 MPa and 30 µs duration. The photodiode signal has been delayed by the time taken for the elastic wave to propagate from the sample to the output-bar gauge position. Reaction occurs whilst the sample is under compression

Full size image

Figure 5 shows an untypical experiment of a PETN sample subjected to a pressure pulse of circa 600 MPa and 30 µs duration, which serves as a helpful example for orientating the later discussion points. The feature that makes the data in Fig. 5 untypical is that, in this case, reaction is observed to occur after the sample has been unloaded, that is, when no forces are acting on the sample; this is the clearest example of such an obviously delayed response from the circa sixty experiments performed in this investigation. The dwell period between unloading and reaction occurring is circa 15 µs. The light from the reaction of the sample coincides with compressive pressure pulses being recorded in both the input and output bars.

Fig. 5
figure 5

An untypical result of a PETN experiment subjected to a pressure pulse of circa 600 MPa and 30 µs duration. The photodiode signal has been delayed by the time taken for the elastic wave to propagate from the sample to the output-bar gauge position. A reaction occurs after the sample has been unloaded and following a dwell period of circa 15 µs

Full size image

From Fig. 5, the magnitude of the compression pulse that is caused by the pressure of the gaseous reaction products mechanically coupling into the bars is of order 500 MPa; a value similar in magnitude to the applied mechanical pressure caused by the action of the striker bar.

A consistent observation of glass-anvil studies [5], is that reaction does not begin at all places at once, rather initiation typically starts at one or a few locations, where so-called critical hot-spots have formed, and then a burning front sweeps out from those sites and consumes the sample.

Our current hypothesis for the lack of an obvious signature of reaction in force records of experiments where reaction occurred under compression, such as Fig. 4, is that the effect of any loss of load bearing solid sample is counteracted by the presence of high pressure product gases as they sweep out from critical hot spot sites, and that due to the moderate confinement condition, the latter replaces the former during the experiment, until such time as the bars come into contact once all the reaction gases have escaped.

The timescales are commensurate with such a hypothesis; as measured by the sentencing photodiode the typical duration for the sample to react is circa 10 µs, which is approximately the same time required for the input bar to traverse a distance equal to the sample thickness. Furthermore, in our recent publication [25] that considers in detail the pressure and temperature induced red-shift of the sodium line, which tends to be the dominant spectral emission feature in the light emitted during reaction, the experimental evidence strongly indicates that the reaction product gasses are in pressure equilibrium with the imposed mechanical pressures.

In principle, with knowledge of the thickness of the specimen, it would be a relatively trivial task to use the normal Hopkinson bar relations [36] to calculate the force–displacement or pressure-density curves for each experiment, which would be of interest. Using a travelling microscope we measured the initial thicknesses of a number of HMX samples and they were of order 320 µm; a value not inconsistent with what one expects if one assumes that the densities in-situ were similar to that in the 40 mm3 dosing spoon. However, it quickly became apparent that with our experimental arrangement, the uncertainties were sufficiently large, and the process sufficiently time-consuming, that for this limited study, where the intention was to demonstrate the feasibility of SHPB initiation, that this aspect was not to be pursued further. This line of enquiry is something that the authors would like to revisit, and we note that to do so rigorously will require taking account of the compression in the bars themselves due to the passage of the pressure waves within them.

Instead, returning to Figs. 4 and 5, there are five aspects that we shall consider in turn: (i) the incident mechanical pressure required to cause reaction, (ii) the mechanical energy absorbed in the run-up to reaction, (iii) the time to reaction, (iv) the idea of a mechanical power or energy threshold for reaction, and (v) the temperature of reaction.

Analysis of Pressure Required to Cause Reaction

Ignoring Pochhammer-Chree oscillations, the nominal mechanical pressures incident on the samples are given by Eq. 7, and using the data of Fig. 5 as an example, a measured impact speed of 30.7 m‧s−1 is equivalent to circa 600 MPa. A plot of mechanical pressure incident on the samples versus binary go or no-go outcome is given in Fig. 6.

Fig. 6
figure 6

The applied mechanical pressures and the responses of the three explosive materials. The vertical lines give the thickness of the observed region of mixed responses; the width spans the range of pressures from the highest measured no-go to the lowest measured go

Full size image

The apparent pressure thresholds shown in Fig. 6 are given in Table 2. These values represent the range of pressures between the highest measured no-go to the lowest measured go, and their mid-points. There was no overlap between the conditions in the case of PETN or RDX, but in the case of HMX seven results fell within the range of mixed results including one partial reaction outcome at 1032 MPa. We call the reaction ‘partial’ because some reaction had clearly taken place, but not all the sample had been consumed, whereas in these experiments a ‘go’ outcome normally left no trace of any unreacted material. It follows that the boundaries between go and no-go conditions are sharp, and the use of sigmoidal stimulus vs. probability of reaction curves, which is the usual approach for impact sensitivity [37], does not seem appropriate here.

Table 2 Pressure threshold data for samples exposed to nominally square-wave pressure profiles
Full size table

Since higher threshold pressures are associated with lower sensitivity, we have that the sensitivity falls as PETN > RDX or HMX. Indicating the usually accepted sensitivity ranking, as would be determined in say a BAM or Rotter test, still holds. As to whether HMX > RDX, this is more contentious, and one can find conflicting reports, a point that is also well made in [35]. Storm et al. [38] would agree with our ranking, Afanas’ev and Bobolev [8] do not. Interestingly, the latter authors do provide critical pressure values for reaction, obtained using instrumented falling weights, and there is good agreement with our values for PETN and RDX, but less so on HMX. Adding to the scope for confusion, as Doherty and Watt point out, impact sensitivities measured on even the same lots of materials on nominally the same type of machine in different labs can vary significantly [39].

However, as attractive a proposition as the data in Table 2 would suggest it is, we would strongly caution against the use of a simple critical pressure threshold for reaction. In the first instance, as Fig. 5 so clearly demonstrates, we have examples of reaction occurring when the instantaneous pressure acting on the specimen is zero.

Additionally, in the case of HMX at least, when we deliberately ramped the mechanical pressure to circa 1200 MPa we saw, over the course of six separate experiments, no reactions. The ramping pressure waves, illustrated in Fig. 7, were generated by placing copper shims at the interface between the striker-bar and the input bar. The use of copper in this manner will change the input pressure pulse to appear as the elastic–plastic stress–strain response of the shim material [40]. This will tend to remove the high frequency content, and give a ramping pressure pulse as a consequence of the shim material work hardening as it flows.

Fig. 7
figure 7

Example of a ramping pressure wave that did not cause HMX to react, despite the pressure exceeding the apparent threshold implied in Table 2

Full size image

Such an observation is reminiscent of the behaviour of shock-induced chemical reactions in Ni/Al powder mixtures, where mixtures react under the influence of strong shocks, but not when more gentle multistep shocks are used to achieve the same final pressure states [41].

Another incident pressure profile that would be worth of study, but which was not explored here, comes from the fact that had a spherical impactor been used instead of a striker bar, then the resulting pressure pulse would be an approximate half-sine [42], and be more reminiscent of, and relatable to, the pressure-pulses generated by falling weight machines. However, it is questionable whether the collision would remain elastic, i.e. the sphere would likely indent the input bar.

Analysis of Energy Absorbed in the Run Up to Reaction

One advantage of using split Hopkinson pressure bars rather than a falling-weight machine is that it is far easier to account for the mechanical energy in the system. The instantaneous mechanical power is given by the product of force and (particle) velocity which can be integrated with respect to time to give energy. Strictly, energy is of course always a positive quantity, and the mechanical energy W associated with either a compressive or tensile wave of magnitude F is given by

$${W}_{wave}^{abs}=\underset{wave}{\overset{}{\int }}\frac{{F}^{2}}{ZA}dt$$
(12)

Equation (12) does not allow us to distinguish between elastic energy associated with compressive or tensile forces. If we instead introduce a sleight of hand, and write the mechanical energy as

$${W}_{wave}=\underset{wave}{\overset{}{\int }}\frac{F\bullet \left|F\right|}{ZA}\bullet dt$$
(13)

then we get the same magnitudes as before, but we preserve the sign: in our convention compression is positive, tension is negative. Clearly, the idea that tension results in negative mechanical energy is an unphysical one, but provided we are careful with our bookkeeping, this is a useful concept.

If the integrations in Eqs. 12 and 13 are not performed, then the products of the integrands and the differential dt, which in practice is the sample interval of our oscilloscope, we shall refer to as the instantaneous energies, wabs and w respectively.

Returning to the example of the delayed PETN reaction shown in Fig. 5, a plot of associated instantaneous energy w, is given in Fig. 8.

Fig. 8
figure 8

The instantaneous energy associated with the delayed reaction of the PETN experiment subjected to a pressure pulse of circa 600 MPa and 30 µs duration

Full size image

We can check the energy of the incident pressure pulse is equal to the kinetic energy associated with the striker bar colliding with the input bar

$${W}_{incident}=\underset{incident}{\overset{}{\int }}\frac{F\bullet \left|F\right|}{ZA}\bullet dt= \frac{{m}_{striker}{v}^{2}}{2}$$
(14)

which it is within experimental error, in the current example these two quantities being (32.1 ± 1.3) and (32.8 ± 0.3) joules respectively.

Making use of our earlier sleight of hand in relation to Eq. 13, we can graphically see that we can isolate the sum of the elastic energies that appear in the reflected and transmitted waves which are due to the elastic collision only, because the energy due to reaction can serendipitously be cancelled out:

$${W}_{reflected+transmision}^{collision}=\underset{transmitted}{\overset{}{\int }}\frac{F\bullet \left|F\right|}{ZA}\bullet dt -\underset{reflected}{\overset{}{\int }}\frac{F\bullet \left|F\right|}{ZA}\bullet dt$$
(15)

and in the current example is equal to (27.9 ± 1.2) joules. The difference between the energies calculated using Eqs. 14 and 15 is therefore equal to that amount of elastic energy that was incident on the specimen that was absorbed in the run-up to reaction, Eabsorbed.

$${E}_{absorbed}=\underset{incident}{\overset{}{\int }}\frac{F\bullet \left|F\right|}{ZA}\bullet dt - \underset{transmitted}{\overset{}{\int }}\frac{F\bullet \left|F\right|}{ZA}\bullet dt + \underset{reflected}{\overset{}{\int }}\frac{F\bullet \left|F\right|}{ZA}\bullet dt$$
(16)

and in the current example is equal to (4.2 ± 1.7) joules.

The above events, being time-separated, make these calculations unambiguous. However, if we make the assumption that stored mechanical energies are mathematically additive, then the above approach will be applicable even when the reaction takes place during the period of compression, and when the collisional and reactive elastic waves are superimposed and otherwise confused. For this approach to be valid, a key underlying assumption is that an equal amount of the energy of reaction is coupled into both input and the output bars.

It is noteworthy that Eq. 16 is unaffected by Pochhammer–Chree oscillations, and may well have merit in the analysis of other experiments of interest, for example, calculating the elastic energy absorbed in the run up to fracture of composites, or converted into thermal energy during the deformation of polymers.

Equation 16 was used to analyse experiments on each material type, the results being summarised in Table 3. Also given in Table 3 are the values reported in the literature, measured using BAM or similar, in particular without sandpaper or roughened surfaces; which act to increase friction and typically reduce the energy of the falling weight required to cause reaction.

Table 3 Elastic energy absorbed by the specimens that reacted, and falling weight literature values
Full size table

In using Eq. 16 we account for all the mechanical energies in the system to isolate that imparted to the samples alone. In a falling-weight machine, similarly; elastic energy is shared by both the sample and the machine and its components, and some energy will be transmitted into the base (floor) and lost. The exact partitioning can only be estimated, but Afanas’ev and Bobolev [8] suggest that about 15–25% of the energy of the falling-weight energy is spent on deforming the samples. At low impact energies the proportion is said to increase considerably, but without obvious quantification, and vice versa. Consequently, we might expect the SHPB threshold energy values to be lower than drop weight values, and indeed this is largely the case.

Compared to traditional methods of assessment, there is a fundamental difference of approach here. Using a falling-weight machine and a Bruceton approach (or similar) one gathers data either side of the threshold, typically for 50% probability of reaction, and attempts to deduce where the threshold is by use of statistics, necessitating N > 1. Using the above SHPB approach one finds the actual value of the amount of energy required to cause reaction, permitting N = 1, that is, an assessment can in principle be made from a single test. Seemingly, the current SHPB approach is more economical in terms of the amounts of material required to form an assessment, although in practice we would always advocate prudence in using as large a value of N as is practically feasible in order to obtain the most reliable statistics.

When obtained in a falling-weight machine, E50 is a probabilistic measure; it is the value at which the chances that a sample will react are 50%. Clearly there is also a chance that a very high-energy impact will be ‘no-go’, and a very low energy impact will ‘go’. This is not the same as the SHPB data, which is the directly measured amount of energy required to cause reaction. The route to reconciliation, or not, may come with a better understanding of the uncertainty of the SHPB data; does it represent a lack of precision, or does it suggest instead an underlying stochasticism?

For all the nominally square-wave pressure pulse experiments instrumented with strain gauges, Eq. 16 was also used to calculate the energies imparted to the samples that did not react. As might be expected, they were in all cases less than the apparent threshold energies, with one exception of an RDX experiment, which nevertheless was just within the bounds of the uncertainties of the threshold. Due to concern over the survivability of the strain-gauges, the ramp-wave HMX experiments utilised PDV only, precluding calculation of the absorbed energies due to the ambiguity in particle speed direction.

As to what the absorbed energies mean in terms of the temperature and physical states of the specimens, then based on the data of [34], Table 4 gives the approximate amount of energy required to raise the bulk temperature to their melt points, to thereafter melt, and the total figure for the process. We do not have information for the temperature and pressure dependencies of the heat capacities, melt temperatures and latent heats, and so have neglected them. Nonetheless, it is noteworthy that the energy absorbed in the run up to reaction is of the same order of magnitude to that amount of energy required to bulk heat the samples to their melt points; in the PETN case falling slightly short, in the HMX case slightly exceeding, and in the case of RDX at least, the total of energy absorbed is comparable to the total amount of energy required to entirely melt the samples.

Table 4 Approximate energies required to raise bulk temperatures to the melt point, and thereafter to melt
Full size table

Analysis of Energy Released  by the Reaction

With reference to Fig. 8 it is trivial to use Eq. 13 and integrate over the reaction pressure pulses to calculate that fraction of the chemical energy that has been mechanically coupled to the bars.

Alternatively, following similar arguments in the construction of Eq. 16, we can isolate the coupled-emitted energy:

$${E}_{emitted}=\underset{reflected}{\overset{}{\int }}\frac{F\bullet \left|F\right|}{ZA}\bullet dt+ \underset{reflected}{\overset{}{\int }}\frac{{F}^{2}}{ZA}\bullet dt$$
(17)

where we make the assumption that the amount of energy launched into the both the input and output bars is identical, which Fig. 8 supports.

Equation 17 is only valid in the case that the reaction pulse is delayed and separated in time from the reflected collisional pulse. If the pulses begin to overlap in time, then Eq. (17) will return erroneous underestimates. Additionally, the F2 term means that Eq. 17 is affected by Pochhammer-Chree oscillations, and this will introduce a small systematic error. Nevertheless, by applying Eq. 17 to the result shown in Fig. 8, we can calculate that the amount of energy that was coupled into the bars was circa (11.2 ± 0.6) joules. Taking the heat of explosion of PETN to be an exothermic value of 5794 kJ·kg−1 [44], then for our circa 31 mg sample mass, we can estimate that approximately 6% of the total chemical energy released was mechanically coupled into the pressure bars.

Analysis of the Time to Reaction

The early research of Bowden and Gurton [45] demonstrated that for PETN and RDX the delay between impact and observed reaction reduces when the velocity of impact is increased. Figure 9 is a plot of applied mechanical pressure versus time to reaction, the difference between the onset of compression to the onset of reaction as indicated by the photodetector. We observe the same behaviour as those earlier authors.

Fig. 9
figure 9

Time to reaction as a function of applied mechanical pressure. The data would suggest that as the mechanical pressure becomes more intense, the observed time to reaction becomes shorter. The inset shows the PETN data and fit of this study, alongside the PETN detonator ‘lost-time’ data of [48]. Note that the longest HMX time to reaction corresponds to the partially reacted sample indicated in Fig. 6. The fits to the experimental data are power laws, the dashed lines are 68% probability bounds for the fitted functions

Full size image

For a concept such as a standalone pressure threshold, a finite time to reaction is a somewhat problematic observation, since it implies, as Fig. 5 clearly demonstrates, that the observed reaction now is in response to an earlier physical condition, and not the presently prevailing one.

Bowden and Gurton noted that the faster the compression the earlier was the explosion, irrespective of the weight, or total energy, of the falling mass. They concluded that the majority of the time between impact and explosion is taken up crushing and compressing the explosive powder, and does not represent an induction period; the experimental result shown in Fig. 5 in part refutes this last statement. Rather, our results would tend to suggest that an amount of work is done which raises the temperature of the specimen, and the quicker this is done the redistribution of heat will be lessened, giving higher temperatures. And that the higher temperatures result in shorter times to reaction; a situation not unlike the so-called one-dimensional time to reaction scenario [46], and sufficiently short that in a falling-weight experiment reaction usually occurs before the impact event is completed.

A complicating factor is that we are not proposing that this temperature rise is uniform throughout the specimen. Rather, we expect that it will be spatially distributed around microstructural features resulting in so-called hot-spots [47]. It is the details of those hot-spot distributions that we expect are changing; either increasing in number density, individual temperature, or both.

An energy based approach is supported by the observation that the power-law fits to the data have exponents of PETN(− 1.7 ± 1), RDX(− 1.5 ± 0.5), HMX(− 2.0 ± 0.8). And mechanical power is proportional to the square of pressure; the implications of which are explored in the next section.

There is much in common here with the concept of so-called lost-time in detonation functioning, and interestingly the PETN exploding bridge-wire and exploding foil initiator data reported by Lee and Drake [48] would appear to be not inconsistent with the extrapolated fit to our split Hopkinson Pressure bar data; see the inset of Fig. 9.

Consideration of a Critical Power or Energy Threshold

Utilised earlier, the relationship that links mechanical power, P, and force in the Hopkinson bar is

$$P= \frac{{F}^{2}}{ZA}$$
(18)

Having expressions for the mechanical power flowing through our specimens, noting the time dependence, and having identified an amount of energy absorbed in the run up to reaction, it is worthwhile to bring these elements together to explore the idea of a critical energy threshold.

Such a proposal is strongly reminiscent of the critical energy concept proposed by Walker and Wasley [49] for describing detonation caused by the launching of strong planar shocks into explosives, which was subsequently modified by James to encompass the presence of lateral release waves [50], and again to encompass heterogeneous explosives [51]. These are ideas that been reviewed recently by Handley et al. [52], and put to use in understanding the role of microstructure in ignition [53, 54]. A modelling based approach applying these ideas to non-shock rapid compression of granular explosives is covered in depth by Barua et al. [55].

Returning to the PETN example shown in Fig. 5, the total energy launched into the specimen, incident minus the reflected energy, was (32.1 ± 1.3) J, and was delivered in circa 29 µs giving an average mechanical power of circa 1.1 MW.

Of the (32.1 ± 1.3) J of energy that was launched into the sample (4.2 ± 1.7) J was absorbed, and the remaining majority passed through the specimen and was carried away by the output bar. The difference between these two values has the physical meaning of the efficiency of mechanical energy absorption. In this case the efficiency factor φPETN = (13 ± 4)%. If this value were higher, the material could be said to be more sensitive; the apparent threshold energy for reaction could be achieved in the same time using lower mechanical powers, that is, with lower applied pressures.

In what follows we assume that the trigger for reaction is thermal in nature, and described by absorption of the energies given in Table 3. In Fig. 10 we plot the average mechanical powers of the pressure waves that were launched into the samples as function of the observed times to reaction. As in the example above, the product of these two quantities is that amount of mechanical energy that was launched into the sample in the run up to reaction. The average measured absorbed energies are plotted as curves of constant energy. Based on the data and the fits shown in Fig. 10, the efficiency factors are given in Table 5.

Fig. 10
figure 10

Plot of average power launched into the specimens against time to reaction; the fits are curves of constant energy. Also shown are curves of constant energy absorbed in the run up to reaction (from Table 3). The ratio of energy absorbed to that launched can be considered as an efficiency factor; i.e. in the case of HMX circa 6% of the energy launched into the specimen is absorbed in the run up to reaction, and 94% passes through and is carried away by the output bar. The fits to the experimental data are power laws, the dashed lines show standard deviations

Full size image
Table 5 Ratio of energy absorbed by the specimens to that launched into them: the so-called efficiency factor
Full size table

Figure 10 suggests that there is a lower mechanical power threshold, below which presumably thermal losses exceed the rate at which heat is accumulated, and reaction does not occur regardless of the loading duration. Note that the presence of such a threshold mechanical power implicitly implies a threshold pressure, as given by Eq. 18.

Thereafter, there is a loading duration threshold, whereby even if the mechanical power is greater than the threshold, if the loading pulse is of insufficient duration, then the amount of absorbed energy is insufficient to cause reaction.

It is an attractive idea to think that the energy absorption mechanisms that gives rise to the efficiency factor might have at least three aspects.

  1. (1)

    A component intrinsic to the material itself, i.e. a perfect single crystal; likely small, since such elastic media typically do not absorb acoustic waves. This is consistent with the observation that single crystals are often remarked to be insensitive to impact [56].

  2. (2)

    A component relating to the dissipative mechanisms associated with disruption of that microstructure by the pressure pulse [57]; which likely dominates, composing of friction, plasticity, fracture, and heating of gasses trapped in interstitial spaces through adiabatic compression. In our experiments, this phase is associated with the period of reflected wave activity, which indicates that the sample is actively being compacted.

  3. (3)

    Once the compaction phase is over, and the sample is nominally being held at constant pressure, and if reaction hasn’t already occurred, a component due to absorption of the elastic wave through the resultant imperfect compact. For example, would the dwell period shown in Fig. 5 have been shorter if the pressure pulse had been of longer duration? The relative size of this contribution is not immediately apparent, but could easily be probed experimentally by the use of striker bars of different lengths.

Temperature of Reaction

Figure 11 shows a pair of typical HMX experimental results, both taken in our SHPB, which confirm our spectroscopic diagnostic result that the temperature remains approximately constant throughout the reaction at the previously measured value of circa 3000 K. Figure 11 also demonstrates that a rising and falling number of emitters, and not a constant number of emitters of rising and falling temperature, is the most likely explanation for the rising and falling light intensity.

Fig. 11
figure 11

Two typical HMX deflagration temperature measurements taken with the optical pyrometer, overlaid with the intensity of light emission. Lower temperatures of circa 3000 K are measured in our SHPB compared to a more typical circa 4000 K measured using the same material in our BAM impact falling-weight machine. The temperature rises very rapidly with the onset of light emission, stays roughly constant during the main period of light emission, and falls with the extinction of light; even though total intensity is rising and falling on longer timescales throughout

Full size image

Across our SHPB data sets the representative measured HMX reaction temperature is (2900 ± 200) K, a value significantly cooler than the corresponding (4100 ± 300) K BAM impact temperature of reaction measured on the same HMX material, using the same pyrometer configuration [25].

At the present time, we consider that the different loading histories and environments in the BAM impact and SHPB experiments may be driving different chemical reactions, or else the same multiplicity of reactions occurring in differing proportions. Robertson and Yoffe [58] reported that decomposition products generated during impact were closer to, but still different from, those generated by thermal decomposition alone, as opposed to true detonation; indicating that the environment could well be playing a role in the details of the chemistry. Consequently, we should not assume that even for the same material, that the reactions that are occurring in one deflagration experiment are the same as those in another having a differing cause.

In the case of the PETN and RDX samples, the representative measured SHPB temperatures of reaction were (4200 ± 300) K and (3700 ± 300) K respectively.

Conclusions

First and foremost; we conclude that it is a practical proposition to study the ignition of explosives by rapid compression in a split Hopkinson bar arrangement, and have demonstrated this fact using granulated samples of the secondary explosives PETN, RDX and HMX.

The chief advantage of using a split Hopkinson bar arrangement over a falling weight instrument is the comparative mechanical simplicity, which allows for the application of equations to understand the forces acting on the specimen, and to properly account for the elastic energy entering and exiting the samples. We have measured the time history of those forces using both strain gauges and heterodyne velocimetry; in our opinion an upshifted HET-V system that is able to disambiguate between compression and tension would likely be the best experimental way forwards.

We have found it useful to sentence our experiments by recording the light emission, and doing so allows us to note the time elapsed from the onset of compression to the onset of reaction. We find that the more intense the loading, the shorter the time to reaction. Additionally, we can analyse the spectral content of the light to say something about the temperature of reaction; we confirm our earlier finding, that for HMX at least, the reaction temperature in the SHPB arrangement is typically less than in a BAM impact experiment.

It is possible to tailor the pressure pulse shape that is incident on the specimen, and though not done here, in principle it ought to be straightforward to calculate resultant pressure-density relations, or so-called compaction curves. Here we have instead focussed on the use of nominally square-wave pressure pulses and the amount of mechanical energy launched into the specimens, and that fraction that is absorbed by the specimens in the run up to reaction; both being quantities that we can calculate from the force histories.

We note that the amounts of energies absorbed are comparable to those amounts required to bulk heat the samples to their melt points, and in the case of RDX at least, to thereafter entirely melt the samples.

In measuring the absorbed fraction of energy launched into the specimens we arrive at a so-called efficiency factor, φ, which for the current experiments is of order 5 – 10%. Because we expect the compaction phase to play an important role in converting mechanical in thermal energy, we postulate that the efficiency factor is a function of the initial microstructure, and propose that it would be instructive to use these approaches to investigate the effect of sample mass, particle size distribution, morphology and porosity in the case of granular explosives, and thermophysically induced damage in the case of polymer bonded explosives. Sample mass is mentioned because in the present study we present absolute energies, whereas specific values normalised to, say, sample mass may well be more appropriate. Thereafter, whether a small or large particle size of a given explosive results in greater or lesser sensitivity becomes a question of how efficiently mechanical energy is converted into thermal energy during the compaction phase, and for the period after that, when mechanical energy is flowing through the unreacted resultant compact.

We propose that there is a lower mechanical power threshold below which heat is lost faster than it can be accumulated. A consequence of this is that there exists a lower pressure threshold for reaction. But neither mechanical power or pressure alone is sufficient information to decide whether reaction will occur or not. The duration of the loading seemingly must be sufficiently long so that the amount of energy imparted reaches some minimum threshold. Since power, energy and time are intuitively linked, we think it is more helpful to think in those terms, and certainly the idea of a stand-alone instantaneous critical pressure is not supported.

In part, our observations may explain some of the confusing results produced by drop-weight instruments. Equal energy drops generated using smaller masses will be of shorter duration, and therefore higher mechanical power, and since our results clearly indicate a dependency on mechanical power, equal energy drops are perhaps not as equavalent as one might at first assume. Similarly, even for the same material, we postulate that different initial microstructures; size distribution, density, etc., may give rise to differing compaction behaviour, and therefore different efficiency factors, that will change the apparent sensitiveness.

In the modelling and simulation publication by Barua et al. [54], the authors comment that: ‘we are mindful of the need to validate the model calculations, but have not yet found data from well-defined comparable experiments with well-characterized microstructures’. The authors would like to suggest that the use of split Hopkinson pressure bars might represent a fruitful experimental way forwards.