Introduction

The speed of sound in water has always been recognized as an important thermodynamic property which is widely used to calculate some acoustic and thermal properties (e.g. isentropic compressibility and the primary acoustic forces in ultrasound assisted demulsification [1]), and also it can be utilized as reference data to calibrate the majority of acoustic detection systems such as hydrophones and sound velocity profilers [2].

After 1826 when Colladon and Sturm launched the first physical-based experiments to measure the speed of sound in water on Lake Geneva, through simply striking an underwater bell on a boat and calculating the time taken for the generated pulse to traverse to another boat over a known distance [3], a variety of time measuring techniques have since been introduced to determine the speed of sound in water. The double-reflector pulse-echo method was commonly used in several investigations, wherein the ultrasonic pulses at the carrier frequencies of 5 [4, 5] and 8 MHz [6] were transmitted in two opposite directions and were then detected by two stationary reflectors at two unequal distances from the transducer. The differences in arrival time of the detected echoes could be consequently used to calculate the speed of sound.

In another study [7], two transducers were immersed in a thermostatic acoustic vessel to transmit and receive ultrasonic signals over various acoustic pathlengths which were measured by a double-beam, plane-mirror interferometer. Here, the time-of-flight technique was used to measure the difference in arrival times of 1 MHz signals over two precisely known distances.

Despite that time measuring studies are carefully planned, executed, and analyzed, so that the speed of sound in water is precisely reported (with uncertainties from 0.001 to 0.003%), there are few experimental data sets that give the speed of sound variation with temperature over a wide range of liquids using this intricate technique. Such data sets are often needed for calibration purposes in ultrasonic systems; consequently, the wave nature-based techniques were developed as another speed of sound measurement method in water as a function of temperature. Here, the frequency (f) and the wavelength (λ) of the ultrasound are measured instead of the time. For the first attempts, Greenspan and Tschiegg [8] managed to measure the pulse-repetition frequencies, corresponding with the end-to-end time of flight of ultrasonic pulses, at 1° C intervals over the temperature range 0° to 100° C. Water was placed in a 200 mm tube with transducers placed at either end. Successive echoes were sent into the tube and the frequencies were obtained on an oscilloscope when time coincidence was observed between the pulses; they were multiplied by twice the tube length, equivalent to λ, to calculate the speed of sound at that particular temperature. Unlike Greenspan’s work, with the fixed acoustic pathlength and adjusted frequency, later efforts [9, 10] were carried out based on variable pathlengths, measured by an ultrasonic interferometer operating at 5 MHz, which allowed determination of the wavelengths for the speed of sound calculations with temperature variation. As a result, the speed of sound in water was measured and reported for 148 observations between 0.001 °C and 95.126° C, with low uncertainty (about 0.015 m/s accuracy). In further studies, Fujii and Masui [11] reported higher precisions in their results (0.001%) over the temperature range 20–75 °C; here they used a carrier frequency of 16.5 MHz and they further employed a Michelson interferometer [12] that was illuminated by a frequency-stabilized He–Ne laser as a comparator to precisely determine the acoustic wavelengths in pure water.

Although there is high reliability of the measurement of the sound of speed by using the universal wave equation, the complexity in wavelength determination at higher frequencies remains a challenge for both of these methods and systems. As the frequency increases into the MHz range, wavelengths of course become shorter and are of the order of microns. Consequently more sophisticated systems are needed to measure the wavelengths precisely, adding to system complexity. In addition, the uncertainty and variability in the results inevitably increases in the speed of sound measurements for liquids other than water or impure water, for which there are no comprehensive data sets for verification of the results. Duplication of these complex systems and methods in the measurements for higher frequencies is difficult to carry out and often yields an accuracy that is greater than is required for many purposes. The current technique proposed is simple and convenient to set-up, providing sufficiently accurate results for many applications. This study aimed to develop a new method, demonstrated using low frequency ultrasound, to measure the speed of sound in water. Lower frequencies were selected in the first case as longer wavelengths (at cm-scales) are more easily measured with less error.

Material and Methods

The new methodology utilized two operating procedures to measure the speed of sound in water within the temperature range of 20–95 °C and were based on the liquid version of the resonance air tube [13,14,15], wherein attaining resonance conditions is targeted to determine the wavelength and coincidence frequency of the propagating waves in the liquid at a set temperature. The coincidence frequency is defined as when the emitted frequency (top of tube) and detected frequency (bottom of tube) are equal.

The two procedures are 1) Acoustic pathlength adjustment, until resonance is met, and determination of the speed of sound at 20 °C, followed by 2) Frequency manipulation of the acoustic field until resonance is met for different temperatures.

The purpose of the first procedure (the variable pathlength method) is to study the amplitude traces resulting from the displacement of the moving transmitter during the ultrasonication in the water-filled acoustic tube, with a fixed frequency of 28 kHz, equal to the resonance frequency of the piezoelectric transducer at 20 °C. To start this task, the acoustic tube was filled with fresh water to the 18 cm mark, and the temperature was set to the initial water temperatures of 20 °C. The transmitter and transducer were interfaced with the water, and the 28 kHz ultrasonication, with peak-to-peak amplitude of 5 V, was applied for 30 s. The time duration was sufficiently long enough to capture 90 root mean square (RMS) voltage readings. After a short delay, this process was repeated for the next locations, where the transmitter was displaced relative to the water surface with a 2–3 mm reduction in its level within the tube, until the two transducers were as close as possible to each other with a water film confined between them.

The wavelength could be then determined through simply measuring the distance between the consecutive, significant voltage peaks which were produced as a result of the variable pathlength method. Therefore, procedure 1 yielded the speed of sound in water at 20 °C by using the universal wave equation. Whilst the amplitude peaks were measured as the transducer was moved towards the emitter, the expectation was that at some point the phase differences between the radiated and received waves will be almost zero at the receiver; this occurs when the gap between transmitter/receiver was approaching the distances equal to an integral number of half wavelengths in the vibrating water column [13]. The distance between the amplitude peaks, therefore, is considered to be the wavelength at 20 °C, yielding the speed of sound in water by the λ∙f relationship.

In order to confirm the resonance frequency of the piezoelectric transducer at 20 °C, another experiment was carried out in the acoustic water tube where the distance between the transducer surfaces was kept equal to the newly calculated wavelength. The frequency applied to the transmitter was then linearly adjusted over the transducer’s operating bandwidth at 28 kHz ± 1.2 kHz, where, of course it was anticipated to get the maximum amplitude at exactly 28 kHz, as confirmation.

The second procedure (frequency manipulation method) investigates the coincidence frequencies corresponding to temperatures higher than 20 °C, while keeping the acoustic pathlength distance equal to the wavelength at 20 °C (as measured in procedure 1). This procedure was repeated over temperature increments of 5 °C up to 95 °C, where it was expected to see a drop in the amplitude trace followed by a slight phase shift across these temperature changes. This indicates degradation of the resonance conditions in the tube. Resonance can be restored by frequency manipulation to the coincidence frequency at each temperature, causing the phase difference to substantially diminish. As a result, the coincidence frequency can be found when the match between receiving frequency and the radiated one occurs. The coincidence frequencies that were found for each temperature were multiplied by the acoustic pathlength to calculate the sound velocity in water over this temperature range and the results were compared to the literature.

The oscilloscope x–y inputs were used to fix the distance between the transducers’ surfaces by displaying the phase between the radiated and received waves until the smallest phase difference was observed, displayed as a straight line on the oscilloscope. Afterwards, even a 1 ºC increase in the temperature would lead to degradation in the resonant field, established at a driving frequency of 28 kHz, followed by a slight increase in the phase shift. The output voltages received by the gain detector also showed the peak amplitude at this frequency.

Compared to other resonance tube work [13,14,15], this study presents a novel way to enhance the precision in the resonance condition detection by using an inexpensive, in-house gain detector using an Arduino microcontroller. The gain detector in conjunction with the receiver and transducer in the tube were used to provide real-time recording of the voltage amplitudes from the ultrasonic irradiation, allowing the point of resonance to be easily identified.

Setup

A. Acoustic water column

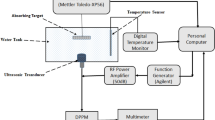
The speed of sound measurements in pure water were performed in a newly designed experimental acoustic system (See Fig. 1). The system primarily consisted of an 84 mm diameter, acrylic cylindrical tube with a moveable, 100 W (maximum power), Ultrasonic Transducer (PZT-4, Beijing Ultrasonic Co., China) as the transmitter at the top of the tube and a mounted PZT-8 Ultrasonic Transducer (Beijing Ultrasonic Co.) as the receiver at the bottom of the tube. Both transducers were flat and with the same diameter (68 mm) and both were centered on the tube ends and parallel to each other, allowing the ultrasonic emitter to provide an axial symmetric vibration relative to the tube and receiver. Hence, a plane wave could be partially established in the acoustic tube as result of the tube geometry around the target frequency of 28 kHz. The circular waveguide cutoff frequency equation was used to calculate the diameter of the resonance tube, using the following relationship [16, 17],

$${f}_{c}=1.841 \frac{{c}_{0}}{\pi d}$$
(1)

where fc is the cut off frequency, c0 is the velocity of sound in water (1582 m/s @ 20 °C), d is the diameter of the tube and 1.841 is the smallest of the radial wave motion propagation constants in the tube, resulting from the derivatives of the Bessel function with the wave number set equal to zero [17]. Due to the need to accommodate the transducers and heater in the resonant tube, a larger diameter was used in this study than would be derived from (1). Therefore, a larger dispersive coefficient, equal to 5.3314 was used to calculate the critical diameter of the resonant tube. This might not, however, result in damped wave propagation, due to the finite length of the acoustic tube [18] which was only about 20 cm in height. It was found that for the 28-kHz device, the inner diameter of the tube must be equal to or less than 9.6 cm, assuming a plane wave tube with arbitrary terminations.

Fig. 1
figure 1

Schematic of the experimental system. Components: 1-Ultrasonic PZT Transmitter, 2-PZT Receiver, 3-Acoustic cylindrical duct, 4-Micromanipulator Clamp, 5-Water Outlet Valve, 6-Cartridge Heating Element, 7-K-Type Temperature Controller Thermocouple, 8- Thermometer used for calibration, 9-Arbitrary Waveform/Signal Generator (AWG), 10-Digital Oscilloscope, 11- In-house Arduino Online Control System (Thermostat-Gain Detector), 12- PC

Full size image

Two ultrasonic transducers were used for the system for transmitting and receiving the acoustic streaming. The transducers were made of two Lead-Zirconate-Titanate (PZT) made piezoelectric ceramic disks, 45 × 7.5 mm, coated with copper–gold alloy electrodes and wholly matched with a rear resonant steel cap and a front aluminum head. The transmitter transducer working frequency was 28 kHz with a ± 1.2 kHz operating bandwidth. It was excited by the specified sinusoidal burst signals which were driven via a dual-channel signal generator (MHS-5200A, 25 MHz, Zhengzhou-Minghe Electronics Tech. Co.,LTD, China). The transmitter was held in place by a micromanipulator clamp to precisely adjust the generated acoustic fields to achieve the desired effect, wherein the interference of the incident and reflected waves would produce superpositioned waves of greater amplitude. The irradiated ultrasonic waves would be repeatedly reflected at the end of their journey though the water column, due to encountering the rigid transmitter/receiver at the end of tube, and then they travel in the opposite direction back to the radiating source, while the source was periodically displaced towards the receiver. The periodic adjustments allowed the acoustic field to successively approach the resonance modes in an iterative fashion. The resonance occurs at equally spaced intervals along the tube, wherein the distance between the transducer and emitter surfaces is equal to an integral number of half wavelengths. Since the piezo transmitter introduces the antinode plane at the interface with the surface of the water, the intervals which lead to the maximum acoustic amplitude detected by the receiver, actually correspond to the pressure antinodes. Therefore, the pathlengths will be equal to a multiple number of half wavelengths. This was called the variable pathlength method, used in achieving the resonant field in the acoustic tube.

A valve was mounted at the bottom of the acoustic tube to allow easy adjustment of the water level and the tube was graduated with a mm scale to facilitate measurement of the acoustic pathlengths.

B. Online control system

At the core of the instrumentation, a real time control system was designed with two open-source microcontrollers with two principal tasks: 1) gain detection and 2) temperature control.

  1. 1)

    The gain detector consisted of an Arduino UNO microcontroller board based on the Microchip ATmega328P microcontroller, and a simple voltage preamplifier to provide noise-tolerant voltages. The microcontroller, in conjunction with a two-channel oscilloscope, was dedicated to real time detection of the acoustic field responses to the ultrasonication carried out in both procedures: the variable pathlength and frequency manipulation methods. The amplitudes of the resultant voltage responses were then processed and computed as the RMS voltages through embedded codes. The Arduino baud rate was 57,600. There was also a serial data link connected from the signal generator’s TTL I/O interface into the microcontroller to capture the driving frequency of the transmitter; this is needed to automatically calculate the speed of sound in water as a function of temperature, which was displayed on the screen.

  2. 2)

    The second Arduino-based microcontroller was developed to accurately control the system temperature so that it was consistent with the differences between the set point and the real temperature; this was coded through an in-house C++ algorithm to maintain thermal equilibrium at the desired temperatures, where the algorithm modulated the power supplied to a 300W cartridge heating element (Wattco, USA). The temperature was measured with a sensitive K-type thermocouple (PTMTCA7, 1 mm diameter, RS PRO, France). The heating element and thermocouple were interfaced to the microcontroller via a power driver circuit and a MAX31855 temperature module (Adafruit Manufactures, NYC), respectively. The thermocouple sensor rod covered the entire water depth, leading to an averaged temperature measurement. By mounting the heating element and thermocouple in the acoustic tube, the temperature fluctuations could be reduced in the tube during the speed-of-sound measurement tests.

In order to improve the homogeneity of the temperature distribution in the water column, the heating element was specifically designed to lead to agitation in the column. The element was fully embedded in a glass tube with a small gap at the end. Here, the water was spontaneously and continuously dragged up into the narrow space between the element and glass tube and then vigorously pushed out as a result of explosive growth of the micro-bubbles generated when the water was in contact with the hot element. Hence, the heat was rapidly and evenly distributed within the entire water column, reducing any thermal gradients. By developing this method of naturally forced convection, there was no need to use an impeller which could potentially produce severe disturbances in the ultrasonic field and electrical interference.

The heating system was examined and calibrated using a laboratory glass thermometer (0.3 °C accuracy, -1/101 °C, Thermometer World, UK) placed inside the acoustic tube. The estimated uncertainty of the temperature measurements was ± 0.25 °C, over the tube volume.

C. Data acquisition

All of the captured and computed data sets were transferred from the microcontrollers to the PC (see, 12 in Fig. 1) through the Parallax microcontroller data acquisition tool (PLX-DAQ, USA,Parallax Inc.) software, at a rate of 3 readings per second. The variation of the speed of sound in water with temperature could then be plotted in real time from a large number of accumulated data readings of the voltage amplitude responses and temperature readings with respect to the frequency manipulations. The signal generator’s built-in GUI provided a platform to monitor and control the acoustic field features. The wave forms, input voltage amplitude and frequency were included in the control panel.

All experiments were repeated three times to obtain an average and standard deviation of the results. In order to filter noisy data in the voltage measurements, an average of 200 samples were captured with a delay of 10 ms between readings. This was repeated 90 times, and these values were then averaged and analysed for procedure 1 and 2 and for the confirmation of the resonance frequency experiments.

The overall uncertainty in the speed of sound in water measurement (uw) was calculated and consists of fractional uncertainties in the temperature (uT), pathlength (uL), and frequency (uf) measurements, given by

$${\mathrm{u}}_{\mathrm{w}}= \sqrt{{\mathrm{u}}_{\mathrm{T}}^{2}+{\mathrm{u}}_{\mathrm{L}}^{2}+{\mathrm{u}}_{\mathrm{f}}^{2}}$$

Results

Fixed Ultrasonic Irradiation over Variable Pathlengths (Procedure 1)

Figure 2 shows the graph of the detected RMS voltage as a function of depth of water in the acoustic tube, with the water held at 20 °C. The emitter frequency was 28 kHz and the resonance locations in the tube are clearly identifiable, with 4 peaks occurring at L = 0.0, 5.3, 10.6 and 16.0 cm. Here, the position of each peak corresponds to a multiple number of half wavelengths of the ultrasonic irradiation. However, the smaller peaks are observed at the half-wavelength condition and the 4 larger peaks correspond to an integral number of full wavelengths at resonance; this indicates that the standing field is likely perfectly formed in the acoustic water column when the distance between the transducer surfaces was strictly equal to an integral number of full wavelengths. It is seen that each peak reduces in amplitude with increasing distance because of the increased power absorption in the water.

Fig. 2
figure 2

The linear alteration in acoustic pathlength vs. the variation in amplitude voltage responses at a water temperature of 20˚C

Full size image

The simultaneous monitoring by the oscilloscope confirmed the uniqueness of these locations, wherein the phase of the radiated and received waves were perfectly overlapping at the driving frequency. The error bars in the plots at every point correspond to 3 data sets, and every point is the average from three runs, with 90 RMS voltage readings for each run.

The wavelength was measured as 53.0 ± 0.1 mm based on the distances between the peaks, resulting in the calculated speed of sound being equal to 1484 ± 3.2 m/s for water at 20 °C at 28 kHz. This indicates an accuracy of 99.89% compared to the reference data [19, 20].

Resonance Frequency Determination

Figure 3 shows the result of keeping the distance fixed and changing the frequency to confirm the resonance frequency of piezoelectric transducer at 20 °C. The RMS voltage amplitudes detected by the gain detector presented a peak at 28 000 ± 1 Hz, equivalent to the resonance frequency. Here there were three runs, with 100 readings collected for each data point shown and the SEM was ± 2.5 mV (for 92.4% confidence level). The test demonstrates the uniqueness of this resonance frequency and validates the speed of sound calculation at 20 °C.

Fig. 3
figure 3

The ultrasonic frequency adjustment vs. the variation in amplitude voltage responses to find the resonance frequency for a water depth of 5.3 cm, equivalent to λ at 20˚C

Full size image

The Coincidence Frequency Determination over Variable Temperature

Following procedure 2, the coincident frequencies were found in the acoustic tube from 20–95 ºC, along with X–Y oscilloscope tracking on the phase shift variations between the radiated and received waves to identify the zero phase shift, as result of the temperature increments; these results can be seen in Fig. 4. The small phase difference between the transmitted and received ultrasonic waves was first quantified with the oscilloscope at the initial temperature and frequency of 20 °C and 28 kHz, respectively.

Fig. 4
figure 4

The impact of temperature on phase difference between radiated and received waves (T- ɸ), associated with the frequency adjustment requirement, (T-f)

Full size image

At 20 °C, when the phase shift was 0, resonance was achieved. This can be seen by the white circle in Fig. 4 and the overlapping black circle shows the 0 phase shift (20 °C at 28 kHz). Keeping the irradiating frequency at this matched condition, the temperature was increased to 25 °C, which took less than 1 min to achieve. The corresponding phase difference increased with this temperature rise. The new phase shift can be seen in Fig. 4 by the square box. The frequency was then adjusted to achieve the resonance condition for this new temperature, the new frequency can be seen, again by the white circle, and the corresponding resonant (coincidence) frequency is shown by the black circle, where the difference between these two represents the observed phase shift to achieve resonance at the new temperature. This was repeated in 5 °C increments.

It should be noted that the required driving frequencies were swept upward and downward before and after 75 °C respectively, in order to minimise the phase difference. It should be noted that the speed of sound in pure water is reported [19, 20] maximum around this temperature.

Figure 5 shows the RMS voltage plotted as a function of frequency over the temperature range 20–95 °C; these data plots identified the coincident frequencies that were plotted in Fig. 4.

Fig. 5
figure 5

The coincidence frequencies observed at temperatures 20(a), 25(b), 30(c), 35(d), 40(e), 45(f), 50(g), 55(h), 60(i), 65(j), 70(k), 75(l), 80(m), 85(n), 90(o) and 95(p)˚C

Full size image

Comparing Figs. 4 with 5 shows that the peak voltages occurred at the moment when the phase differences between the radiated and received waves were at their minimum, corresponding to the coincident frequencies.

The Speed of Sound in Water over Variable Temperature

Using the coincident frequency data from Fig. 4, where over 3.2 × 104 readings were taken at the 16 temperatures from 20° to 95° C, the calculated values of the speed of sound were plotted and can be seen in Fig. 6.

Fig. 6
figure 6

The calculated speed of sound in water vs. temperature (Exp) curve fitted with a third order polynomial (Excel, Poly.Exp), compared to the reference experimental data, Del Grosso and Mader [19] and IAPWS-95 equation of state [20]

Full size image

In this figure, each experimental data point was averaged over 4 experimental runs in which the speed of sound was calculated for each temperature. This was carried out to enhance the degree of reproducibility of procedure 2, and to increase the accuracy of data. The data were fitted with a third-degree polynomial with a coefficient of correlation of 0.9856. As can be seen from Fig. 6, there is a good agreement of the fit compared to two sets of reference data [19, 20] plotted alongside.

Table 1 shows the error source for the speed of sound measurements, its uncertainty and relative error in the speed of sound as a function of temperature for this technique. It can be seen that the calculated error was 2.157 × 10–3 percent, corresponding to an error of about 3.2 m/s in the speed of sound of water at 20 °C and 28 kHz.

Table 1 Estimated uncertainty in the speed of sound measurement
Full size table

Conclusion

A novel, low frequency ultrasound assisted methodology was developed to determine the speed of sound in water over a temperatures range of 20–95 °C. The averaged measurements provided the speed of sound as a function of temperature for pure water with a mean square error (MSE) equal to 3.0948, and comparable to the reference data [20]. The high resolution associated with the design simplicity of this approach has demonstrated that the methodology can be used to determine the temperature dependency of the speed of sound in water, with it being equally applicable to other liquid media, with an acceptable level of accuracy. However, 28 kHz might not be an appropriate low frequency for liquids that are denser than water because of the accuracy needed in determining the spatial separation of the nodes.