Bi-DNE: bilayer evolutionary pattern preserved embedding for dynamic networks

Abstract

Network embedding is a technique used to generate low-dimensional vectors representing each node in a network while maintaining the original topology and properties of the network. This technology enables a wide range of learning tasks, including node classification and link prediction. However, the current landscape of network embedding approaches predominantly revolves around static networks, neglecting the dynamic nature that characterizes real social networks. Dynamics at both the micro- and macrolevels are fundamental drivers of network evolution. Microlevel dynamics provide a detailed account of the network topology formation process, while macrolevel dynamics reveal the evolutionary trends of the network. Despite recent dynamic network embedding efforts, a few approaches accurately capture the evolution patterns of nodes at the microlevel or effectively preserve the crucial dynamics of both layers. Our study introduces a novel method for embedding networks, i.e., bilayer evolutionary pattern-preserving embedding for dynamic networks (Bi-DNE), that preserves the evolutionary patterns at both the micro- and macrolevels. The model utilizes strengthened triadic closure to represent the network structure formation process at the microlevel, while a dynamic equation constrains the network structure to adhere to the densification power-law evolution pattern at the macrolevel. The proposed Bi-DNE model exhibits significant performance improvements across a range of tasks, including link prediction, reconstruction, and temporal link analysis. These improvements are demonstrated through comprehensive experiments carried out on both simulated and real-world dynamic network datasets. The consistently superior results to those of the state-of-the-art methods provide empirical evidence for the effectiveness of Bi-DNE in capturing complex evolutionary patterns and learning high-quality node representations. These findings validate the methodological innovations presented in this work and mark valuable progress in the emerging field of dynamic network representation learning. Further exploration demonstrates that Bi-DNE is sensitive to the analysis task parameters, leading to a more accurate representation of the natural evolution process during dynamic network embedding.

Introduction

Primary motivations

Citizens have shifted from traditional media to online social networks (OSNs) for obtaining, exchanging, and sharing information. The vast amount of data collected on OSNs are invaluable for academics and economics, making these platforms truly remarkable. This situation has led to the creation of many machine learning algorithms that address different application tasks, such as community detection [1, 2], link prediction [3, 4], node classification [5, 6], data visualization [7], and user alignment [8]. The volume of available social network data and the reliance of methods on the quality of the input pose challenges for implementing machine learning algorithms [9, 10]. To overcome these obstacles, various representation learning techniques have been proposed.

Network embedding (NE) is a type of representation learning strategy that has become popular for solving social network tasks. NE is further divided into static network embedding (SNE) and dynamic network embedding (DNE). SNE is commonly used in the OSN research and is employed to extract various user node features, such as text sentiments and user relationships in social networks. In SNE methods, the vertices and edges remain unchanged during the time evolution process. DSRE [11], an unsupervised method introduced by Xiao et al., is a cost-effective way to extract specific knowledge from the abundant unstructured text information available in OSNs. Its efficacy has been proven to facilitate efficient OSN research while minimizing experimental costs. However, real-world networks are dynamic and constantly evolving. OSNs, such as Facebook and microblogging sites, offer opportunities for users to meet new people and build lasting connections, resulting in the constant formation of new friendships. The constantly changing nature of network development poses new challenges for SNE problems. Therefore, representation learning algorithms that overlook these dynamic features face limitations in terms of accurately capturing the evolving characteristics of hidden nodes, thus impeding their effectiveness in various practical applications.

A DNE approach extends a conventional static network model to capture the evolving patterns within networks [12, 13]. Li et al. [14] employed matrix perturbation theory to iteratively update low-dimensional node vectors, considering the temporal dependencies between different network representations. Goyal et al. [15] utilized a deep autoencoder called DynGEM to capture the nonlinear information between neighboring nodes, enhancing the learning of first-order and second-order relationships. While these DNE methods have provided some insights into network evolution, they still fall short of discerning the distinctive characteristics of the various node types within a network. Moreover, there is a dearth of comprehensive knowledge surrounding the fundamental dynamic mechanisms that drive network structure shifts.

Previous research has demonstrated that network dynamics are heavily influenced by evolution, with triadic closure being one of the most important structures [16]. Closed triads are formed when all pairs of users have connections in subsequent snapshots. The significance of triadic closure cannot be underestimated in terms of the growth and progression of OSNs. Importantly, this mechanism is not exclusive to OSNs; it also applies to the natural patterns that are present in various types of networks. Figure 1 depicts the evolutionary patterns observed in the vertex and community structure of a local social network. i and j are initially unconnected users, and they establish a friendship with user kat time a. This pattern unfolds in three distinct phases. Initially, user k exhibits relatively low connectivity, indicating limited popularity. However, user k can its increase attention and effort by maintaining strong connections with these two friends. Subsequently, user k evaluates the relevance and similarity between themselves and users i and j. This evaluation guides user k’s social strategy, determining whether it is advantageous to introduce their two friends to each other. In OSNs, communities are typically subgraphs with higher internal link densities than that of the overall network. The likelihood of forming connections within a community surpasses that of forming connections between different communities. In Fig. 1, i and j are not initially part of the same community, necessitating k’s role in fostering connections across communities. As time passes and triadic closure occurs, users i and j may change their link structures. This can lead to significant dissimilarity in their low-dimensional representations. Consequently, the community structure that they inhabit also undergoes an alteration.

Although past studies have recognized the impacts of alterations on network dynamics and the significance of incorporating events such as triadic closure into the development of social networks, little research has adequately merged DNE with triadic closure to address problems within OSNs. Yang et al. [17] presented DNETC, a novel DNE model that combines DNE coordination and triadic closure to effectively capture network evolution patterns. Their approach employs an ensemble technique using vertex similarity and emphasizes two factors, vertex popularity and community structure, enhancing the learning of a discriminative low-dimensional network representation. By incorporating this feature-enhanced representation, the authors optimized the evolution process of triadic closure within the network. However, understanding network evolution requires the consideration of both the micro- and macrolevels. The microlevel captures the intricate formation process of the network structure, involving the gradual generation of new edges through strengthened ternary closure. It provides insights into the specific structure adopted by the network at a given time, explaining the evolution process of the network. In contrast, macrolevel dynamics focus on network size changes, which are measured by the quantity of edges. This dynamic evolution process exhibits discernible nonrandom patterns and aims to answer the question of “how many edges should be generated in total by the dynamic evolution process of the network at the microlevel at time t.” Understanding the dynamics at both the micro- and macrolevels is crucial for comprehending the evolution of a network, as these factors significantly influence how networks grow and transform.

Fig. 1

Evolutionary patterns of vertices and the resulting community structures in localized social networks. The red solid line represents the addition of a new link at the subsequent moment. The circles with different colors represent the discrete vertices of two communities

Innovation aspect

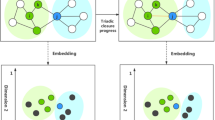
This study proposes bilayer evolutionary pattern-preserving embedding for dynamic networks (Bi-DNE), which is a novel approach for dynamic network representation learning that captures evolution patterns at both the micro- and macrolevels, thus addressing the challenges associated with network representation learning in dynamic networks. Bi-DNE offers methodological innovations in terms of network representation learning by integrating triadic closure and dense power laws. We use enhanced triadic closure to simulate how dynamic network structures change at the microlevel. At the macrolevel, we use dense power-law principles to impose constraints on how a network structure evolves. Our method effectively captures the dynamic characteristics of the network evolution process through low-dimensional representations, showcasing its methodological advancements. The visualized pipeline offers a clear and concise representation of the Bi-DNE method, as described in Fig. 2. The process begins with the input of a dynamic network and then divides it into two primary components that represent the micro- and macrolevel dynamics. It then learns the community structure of the network and finally converges to the Bi-DNE embedding process. The result is an evolved network representation that effectively demonstrates the fusion of micro- and macrodynamics during dynamic network embedding.

Fig. 2

A visualization pipeline of Bi-DNE

The Bi-DNE model is tested through various experiments that involve link prediction, link reconstruction, changed link prediction, and reconstruction tasks conducted on real datasets. Through these experiments, it is shown that the model can accurately preserve dynamic network evolution patterns. Our proposed model successfully captures high-quality feature representations from social network data. These findings underscore the methodological innovations and practical value of the Bi-DNE algorithm.

Contributions

The specific contributions of this study are listed below:

• Bi-DNE, a new approach that integrates micro- and macrodynamics to learn embeddings for dynamic networks, captures the natural evolution process of a network and improves network analysis tasks, is presented.

• Microlevel modeling is performed via enhanced triadic closure to capture granular network formation.

• Macrolevel modeling constrains the overall growth trends through a power law.

• Multiscale dynamics unification enables the evolution process to be more accurately represented.

• The proposed approach significantly outperforms the baselines on predictive tasks concerning time-evolving networks.

• This study advances the state-of-the-art representation learning research for dynamic networks.

• The sensitivity of the parameters in Bi-DNE is validated for the analysis task, demonstrating that the network representations learned by Bi-DNE are capable of addressing different types of variations.

Manuscript structure

The rest of the paper is organized into the following sections. The section “Related work” provides a brief review of related work. The notation and definition of the DNE problem are given in the section “Problem definition”. The section “Framework of Bi-DNE model” presents the Bi-DNE model in detail and the section “Experiment settings” presents the experimental setup. The section “Results” analyzes the experimental results and the section “Conclusion” concludes the paper.

Related work

In this section, we will discuss the various approaches to NE models, both static and dynamic, as explored in previous research. Abbreviations involved in the full text are enumerated in Table 1 for easier understanding.

Table 1 List of abbreviations

SNE models

In the early stages, matrix factorization techniques, such as Laplacian eigenmapping [18] and locally linear embedding (LLE) [19], were commonly used. These approaches aim to obtain node representations of dimensionality k by computing eigenvectors. However, they often face challenges, including high computational costs and statistical performance limitations, when dealing with large-scale networks.

Deep learning has emerged as a prominent approach for network representation learning, leveraging neural network-based models to capture the intricate patterns and relationships within a network. DeepWalk [20] draws inspiration from the skip-gram word representation model [21] and learns latent representations. Node2Vec [22] extends DeepWalk by introducing a bias parameter that enhances the walking strategy by controlling the preference for depth- or breadth-first search. Line [23] focuses on capturing the second-order proximity information by considering the common neighbors of indirectly connected nodes, complementing the information acquired from the first-order proximity. SDNE [24] utilizes a deep neural network, modeling the highly nonlinear relationships between node representations, and uses the middle layer of a deep autoencoder to represent network nodes. GraRep [25] incorporates a specific relation matrix and reduces its dimensionality through singular value decomposition, resulting in a k-step network representation. These deep learning-based models have advanced the field of network representation learning by effectively capturing complex network structures.

The existing methods primarily focus on preserving the pairwise relationships between nodes while overlooking the valuable community structures in networks. Notable approaches such as BIGCLAM [26] and MemeRep [27] incorporate community structures into the network embedding (NE) process, but they do not consider the dynamic evolution characteristics of the target network. To obtain precise network representations, it is essential to include diverse and varied external information alongside the network topology. TADW [28] addresses this issue by incorporating the text features of nodes through matrix factorization, enhancing the strength and effectiveness of network node representations. CANE [29] is another noteworthy method that captures contextual information by considering node neighbors, improving the quality of the resulting network representations. These approaches provide insights into the integration of community structures, external information, and contextual dependencies for effective network representation learning. Li et al. [30] proposed using neural networks to learn node embeddings that capture air transportation network features. These embeddings were utilized to predict market influences for flight frequency optimization. In addition to network topology information, incorporating node attribute information into embeddings has shown promise. Li et al. [31] modeled the influence propagation process by jointly representing users in a social network structure and a multidimensional attribute space.

DNE models

Many methods have been suggested for preserving evolutionary trends in dynamic networks. DANE [14] and DHPE [32] employ matrix perturbation theory and generalized singular value decomposition to update node vector representations in dynamic networks while preserving high-order proximity. DNE [33] enables separate learning of node embeddings, enhancing the efficiency of vector representation updates. These methods contribute to preserving evolutionary patterns in dynamic networks by incorporating different techniques for updating node vector representations. Yu et al. [34] introduced NetWalk, a clique-based DNE approach for anomaly detection. Zhou et al. [35] proposed a method that incorporates dynamic information into a vector representation. A triadic closure simulation mechanism helps their model achieve excellent results. Ma et al. [36] presented a smoothing technique to maintain continuous community dynamics. This community-aware mechanism greatly improves the model fitting degree of real community change. CTDNE [37] is a dynamic network that captures time sequence information with continuous-time series represented as random walk sequences. The influence of past neighbors on neighbor formation for node vector representations is captured by HTNE [38] using the Hawkes process. However, the driving force behind the evolution of dynamic networks, especially the vertex evolution patterns, is often overlooked by these methods.

Lu et al. [39] proposed a novel approach for representing temporal networks by incorporating both micro- and macrodynamics, enabling the modeling of temporal dependencies and capturing microlevel network evolution. Additionally, they addressed macroscopic dynamics by defining a generic dynamical equation parameterized with network embeddings. This equation captured the inherent evolutionary patterns of the network and imposed constraints on the embeddings at higher structural levels. By considering both micro- and macrodynamics, their approach acknowledged the mutual influence between these dynamics and their impact on node embedding learning in temporal networks. The innovative combination of micro- and macrodynamics in their work has served as an inspiration for our own research.

Zhou et al. [40] introduced DynamicTriad, a novel representation learning method that preserves the structural information and evolution patterns of networks. They proposed using triples, comprising three vertices, to capture the fundamental triadic closure process that drives network formation and evolution. By incorporating this process into their model, DynamicTriad effectively captures network dynamics and learns vertex representation vectors at different time steps. This innovative approach provides insights into the temporal dynamics of networks and holds promise for network representation learning. Zhang et al. [41] designed a dynamic graph convolutional network to extract structural embeddings for DNE. Their method learns node representations via a leader-based fake labeling scheme. DynamiSE, proposed by Sun et al. [42], is a novel approach for link prediction that encodes both the dynamic and symbolic semantics of a network. The model integrates balance theory and ordinary differential equations in combination with node representation learning to build a deeper dynamic signed graph neural network. This network is designed to capture the complex symbolic semantics formed by two types of edges, resulting in a more comprehensive and accurate representation of the underlying network dynamics.

Yang et al. [17] proposed a novel network embedding approach for dynamic networks. This method considers vertex similarity and incorporates user popularity and community structure information to capture evolution patterns. By employing the ensemble idea and quantifying the probability of closing open triples, DNETC effectively captures the dynamics of network evolution. Additionally, the authors enhanced the discriminative power of low-dimensional network representations by utilizing community structure information as a higher order proximity measure for vertices. This optimization process yields improved dynamic network evolution predictions and aids in discovering macroscopic community structures. DNETC successfully captures diverse evolutionary patterns while preserving dynamic information in real networks. Du et al. [43] proposed ERM-ME to divide emotional communities based on user emotional preference. Then, the sentiment features are used to train the base classifiers, which are combined into a meta-classifier. Zhang et al. [44] introduce a novel method called DINE that learns vertex representations for dynamic networks. Their approach models users and items concurrently and integrates their representations in dynamic and static information networks.

To provide a more intuitive summary of previous studies, Tables 2 and 3 highlight the strengths and limitations of related SNE and DNE approaches, respectively. Early SNE approaches, such as DeepWalk [20], Node2Vec [22], and LINE [23], have been successful in modeling network topology. However, they do not consider the temporal nature and dynamics of real-world networks. Nevertheless, the initial DNE techniques that rely on matrix perturbation theory or factorization, such as CTDNE [37] and DANE [14], do not fully model the complex microlevel processes that underlie network formation over time. In the work of Yang et al. [17], community information and triadic closure rules are embedded, but the realistic constraint problem of dense power laws is not considered.

This paper proposes Bi-DNE, an improved model that uses an enhanced triadic closure process to simulate the formation of microlevel networks. This model takes important factors, such as node similarities and community structures. Additionally, macrolevel dynamics are governed by a power-law equation that controls the evolution scale of the target network. The fusion of both micro- and macrodynamics enables more precise characterizations of network evolution patterns. This approach can address the limitations of previous research and provide a better understanding of the network formation and evolution process.

Table 2 A detailed comparison of the SNE studies

Table 3 A detailed comparison of the model proposed in this paper and other DNE studies

Problem definition

In this section, we introduce the notations and definitions used throughout our work. The variable symbols and their meanings involved in this paper are listed in Table 4.

Table 4 List of variables

Definition 1

(Undirected network) A dynamic network is defined as a sequence of undirected graphs, represented as network snapshots ${G^{(1)},G^{(2)},\ldots ,G^{(T)}}$, where T denotes the set of finite time steps. At each time step $a\in \left\{ {1,2, \ldots ,T} \right\}$, the network state is denoted as ${G^{\left( a \right) }} = \left\{ {V,{E^{\left( a \right) }},{W^{\left( a \right) }}} \right\}$, where V is the set of nodes, ${E^{\left( a \right) }}$ is the set of edges, and each edge $e_{ij}^{\left( a \right) }$ represents the connection between nodes $v_i$ and $v_j$ with weight $w_{ij}^{\left( a \right) }$. The edges in ${E^{\left( a \right) }}$ are undirected in networks. This definition assumes that the network topology evolves over time rather than remaining static.

Definition 2

(Dynamic network embedding) Let $G =$$\{G^{(1)},G^{(2)},\ldots ,G^{(T)}\}$ be a dynamic network, where T snapshots represent the network at different time steps. A positive integer d denotes the dimension of a low-dimensional representation space $\mathbb {R}^d$. The mapping $f^{(a)}: V^{(a)} \rightarrow \mathbb {R}^{(d)}$, for $a\in \{1,2,\ldots ,T\}$ refers to a function that embeds vertices $V^{(a)}$ in snapshot $G^{(a)}$ into d-dimensional vectors. Let $\varvec{v}_i\in V$ denote vertex i and $\varvec{u}_i^{(a)}$ its corresponding low-dimensional representation. The mapping function f is assumed to learn low-dimensional representations u that can express features of both network topology and dynamics.

Definition 3

(Microevolution pattern) Given a dynamic network, the microscopic microevolution pattern refers to the network structure’s formation process through triads. An open triad $\left( {{v_i},{v_j},{v_k}} \right)$ evolves into a closed triad. The set $\;E_ + ^{\left( a \right) } = \left\{ {{e_{ij}}\mid {e_{ij}} \notin {E^{\left( a \right) }} \cap {e_{ij}} \in {E^{\left( {a + 1}\right) }}} \right\}$ is defined to represent the new edges generated during this process. Triadic closure between time steps is assumed to be one of the primary microlevel drivers of network evolution.

Definition 4

(Macroevolution pattern) Given a dynamic network, the macroevolution pattern at the macroscopic level represents the evolution process in which the network scale follows a certain distribution rule. The notation $A = \left\{ {n_\textrm{e}^{\left( 1 \right) },\;n_\textrm{e}^{\left( 2 \right) },\; \ldots ,\;{n_\textrm{e}}^{\left( T \right) }} \right\} \;$ is defined to represent the set of edge numbers for T time steps of the dynamic network, where $\;n_\textrm{e}^{\left( a \right) }$ represents the total number of edges in the network up to time point a. The evolution of network edge numbers is assumed to follow certain statistical distribution laws, reflecting macrolevel network evolution characteristics.

Definition 5

(Community structure) Communities in dynamic networks consist of nodes that are densely interconnected within each community while having sparse connections with nodes outside the community. Let $\;{C^{\left( a \right) }}=$ $\left\{ {C_1^{\left( a \right) },C_2^{\left( a \right) }, \ldots ,C_m^{\left( a \right) }} \right\}$ represent the division of the network at time a into m communities. Then, we have $V = C_1^{\left( a \right) } \cup C_2^{\left( a \right) } \cup \ldots \cup C_m^{\left( a \right) }$, and for any pair of nodes $\left( {i,j} \right)$ with $i \ne j$, it holds that $C_i^{\left( a \right) } \cap C_j^{\left( a \right) } = \emptyset$. The network is assumed to exhibit community structure characteristics, where nodes have dense connections within communities but sparse connections between communities.

Framework of Bi-DNE model

This section comprehensively introduces the proposed dynamic network representation learning model (Bi-DNE) and its details. Bi-DNE includes three components: multigranularity attribute embedding (the sections “Preservation of dynamic embedding through microscopic evolution”, “Preservation of dynamic embedding through macroscopic evolution and “Microscopic and macroscopic representations of dynamic evolution”), attention-based structure embedding (the section “Preservation of dynamic embedding through community structure”), and an iterative training process (the section “Conjunctive model”). Among them, the multigranularity attribute embedding method comprises two essential processes: the micro-level enhanced triadic closure process, which models network structure formation (the section “Preservation of dynamic embedding through microscopic evolution”), and the macrolevel constraints that enforce a dense power-law evolution pattern through dynamic equations (the section “Preservation of dynamic embedding through macroscopic evolution”). Figure 3 illustrates the framework of Bi-DNE, providing informative details about its structure.

Preservation of dynamic embedding through microscopic evolution

In a social network, when an open triple arises at a certain time, certain users actively introduce their friends, thus transforming it into a closed triple. Conversely, other users opt to maintain the original social status of their friends, thereby displaying a decision distinction based on individual considerations and variations in social strategies. User considerations encompass factors, such as user popularity, similarity, and the community structure to which they belong. As the network evolves, its nodes continually form new connections through the triadic closure mechanism, taking place at various points in time. This evolutionary process is influenced by factors, such as node popularity, similarity between nodes, and the community in which the nodes reside.

Fig. 3

Schematic diagram of the Bi-DNE model. Bi-DNE retains the evolution pattern and community structure of the vertices as the microscopic expression during the embedding process and uses the dynamic equation to constrain the network structure to obey the densified power-law evolution pattern as the macroscopic expression

Considering the aforementioned factors, we utilize a d-dimension vector $\varvec{D}_{i j k}^{(a)}$ to assess the decision of user $v_k$

$$\begin{aligned} \varvec{D}_{i j k}^{(a)}=\left[ \frac{w_{i k}^{(a)}}{{deg}_{k}^{(a)}} *\left( \varvec{u}_{k}^{(a)}-\varvec{u}_{i}^{(a)}\right) +\frac{w_{j k}^{(a)}}{{deg}_{k}^{(a)}} *\left( \varvec{u}_{k}^{(a)}-\varvec{u}_{j}^{(a)}\right) \right] * \xi _{i j}^{(a)}, \end{aligned}$$

(1)

where the edge weight $w_{i k}^{(a)}$ denotes the tie strength of $v_i$ and $v_k$, ${deg}_k^{(a)}$ is the degree of $v_k$, and $\varvec{u}_{k}^{(a)}$ denotes the embedding vector of $v_k$. $\xi _{i j}^{(a)}$ is defined as a function of community influence, that is

$$\begin{aligned} \xi _{i j}^{(a)}={\left\{ \begin{array}{ll} \alpha , &{}\quad \text{ if } {(v_i^{(a)} \in C_p^{(a)})}\bigwedge {(v_j^{(a)} \in C_q^{(a)})}\bigwedge {(p \ne q)},\\ 1 - \alpha , &{}\quad \text{ otherwise }. \end{array}\right. }\end{aligned}$$

(2)

Furthermore, to calculate the probability of an edge forming between users $v_i$ and $v_j$ under the influence of user $v_k$ at time step $a+1$, use the following formula:

$$\begin{aligned} P_{{k \rightarrow i, j}}^{(a)} = \frac{1}{1+\exp \left( -\left\langle \varvec{\theta }, \varvec{D}_{i j k}^{(a)}\right\rangle \right) }, \end{aligned}$$

(3)

where the vector $\varvec{\theta }$ with d-dimensions represents the social strategy information extracted from latent vertices.

Consequently, the probability of creating a new connection follows the formula below:

$$\begin{aligned} P_{e_{i j_{+}}}^{(a)}=\sum _{\varvec{\mu }_{i, j}^{(a)} \ne 0} \prod _{k \in C N_{i, j}^{(a)}}\left( P_{k \rightarrow i, j}^{(a)}\right) ^{\mu _{k \rightarrow i, j}^{(a)}} *\left( 1-P_{k \rightarrow i, j}^{(a)}\right) ^{\left( 1-\mu _{k \rightarrow i, j}^{(a)}\right) }. \end{aligned}$$

(4)

The vector $\varvec{\mu }{i,j}^{(a)} = ({\mu {k \rightarrow i, j}^{(a)}}){k \in {\text {CN}}{i,j}^{(a)}}$ indicates the state of an open triad involving nodes $v_i$ and $v_j$ at time step a. Specifically, $\mu _{k \rightarrow i, j}^{(a)} = 1$ if nodes $v_i$ and $v_j$ will form an edge at time step $a+1$ under the influence of their common neighbor $v_k$. The set ${\text {CN}}{i,j}^{(a)}$ contains all common neighbors of nodes $v_i$ and $v_j$ at time step a. The vector $\varvec{\mu }{i,j}^{(a)}$ encodes which open triads will close due to triadic closure in the next time step. The probability of not generating edge $e_{ij}$ at time $a+1$ follows the formula below:

$$\begin{aligned} P_{e_{i j_{-}}}^{(a)}=\prod _{k \in C N_{i, j}^{(a)}}\left( 1-P_{k \rightarrow (i, j)}^{(a)}\right) . \end{aligned}$$

(5)

The loss function for the triadic closure process combines two user edge evolution patterns with the objective of minimizing negative log-likelihood, which is below [17]

$$\begin{aligned} L_{t}^{(a)}=-\sum _{(v_i, v_j) \in S_{+}^{(a)}} \log P_{e_{ij_{+}}}^{(a)}-\sum _{(v_i, v_j) \in S_{-}^{(a)}} \log P_{e_{ij_{-}}}^{(a)}, \end{aligned}$$

(6)

where $S_{+}^{(a)}={(v_i, v_j) \mid e_{ij} \notin E^{(a)} \cap e_{ij} \in E^{(a+1)}}$ represents the set of open triads composed of nodes $v_i$ and $v_j$ that become closed at time step $a+1$. In other words, $S_{+}^{(a)}$ contains node pairs $(v_i, v_j)$ that do not have an edge $e_{ij}$ in snapshot $E^{(a)}$, but gain an edge $e_{ij}$ in snapshot $E^{(a+1)}$. $S_{-}^{(a)}={(v_i, v_j) \mid e_{ij} \notin E^{(a)} \cap e_{ij} \notin E^{(a+1)}}$ indicates open triads that remain open, i.e., node pairs $(v_i, v_j)$ that do not have an edge $e_{ij}$ in snapshot $E^{(a)}$ and continue not to have an edge $e_{ij}$ in snapshot $E^{(a+1)}$. The sets $S_{+}^{(a)}$ and $S_{-}^{(a)}$ categorize open triads based on whether they close or remain open between time steps a and $a+1$.

Preservation of dynamic embedding through macroscopic evolution

The ternary closure evolution process at the microlevel continuously drives network node topology changes, which are manifested in the continuous formation of new edges. At the macrolevel, the formation process is constrained by the network size, which determines the number of edges to be generated at a given time. Macrolevel dynamics encompass the evolution pattern of the network size, which typically follows a distinct distribution. This distribution allows the network size to be described by a dynamic equation. Incorporating this high-level structure into the network embedding process greatly enhances its effectiveness. Therefore, establishing a dynamic equation with a network embedding vector as a parameter establishes a connection between the network dynamics analysis and DNE tasks.

In a dynamic network, we use the notation ${G^{\left( a \right) }} = \left\{ {V,{E^{\left( a \right) }},{W^{\left( a \right) }}} \right\}$ at time a. Here, V represents the set of nodes, ${E^{\left( a \right) }}$ represents the set of edges, and ${W^{\left( a \right) }}$ represents the weights associated with the edges. The total number of nodes in the network is represented by ${n^{\left( a \right) }}$, while the total number of edges is represented by $n_\textrm{e}^{\left( a \right) }$. The dense power-law model describes the network evolution process, stating that as the graph becomes denser over time. Based on this model, we define the average number of accessible neighbors for each node when attempting to establish a new edge with another node in a dynamic network

$$\begin{aligned} n_{a c}=\varphi \left( n^{(a)}-1\right) ^{\omega }, \end{aligned}$$

(7)

where $\varphi$ represents the linear sparse index and $\omega$ represents the dense power index. Typically, $\omega$ falls between 1 and 2. A value of 1 for the index a indicates a constant average number of degrees over a specified timeframe, while a value of 2 signifies a highly dense configuration.

The link rate r(a) is crucial in developing network size, but its importance diminishes as the network progresses due to its temporal dynamics. This is because the majority of edges are formed in the early stages, and as the network becomes denser, the edge generation rate naturally decreases. The link rate r(a) is also influenced by the underlying network topology. Since the network structure is not static but evolves with new edges, considering this aspect in network embedding is essential. Aiming at incorporating both the temporal and structural information, we propose a parameterized formulation for the network’s link rate using the network dynamic finalization term $a^\epsilon$ and the node embedding $\mathcal {U}$, which can be expressed as follows:

$$\begin{aligned} r(a)=\frac{\frac{1}{n_{\textrm{e}}^{(a)}} \sum _{e_{i j}^{(a)} \in E^{(a)}} \sigma \left( -\left\| \varvec{u}_{i}^{(a)}-\varvec{u}_{j}^{(a)}\right\| _{2}^{2}\right) }{a^{\epsilon }}, \end{aligned}$$

(8)

where $\epsilon$ is network dynamic end item, $\sigma x = \exp \left( x \right) /$ $\left( {1 + \exp \left( x \right) } \right)$ is the sigmoid function. When network evolution is complete, the current network consists of $n^{(a)}$ interconnected nodes. At time a, each node $v_i$ within the network endeavors to form new connections, specifically with other accessible neighbor nodes $n_{ac}$, utilizing a connection rate denoted as r(a). Henceforth, we define the macrolevel network dynamics at time a as the quantity of newly established edges as follows:

$$\begin{aligned} \Delta n_{\textrm{e}}^{\prime (a)}=n^{(a)} * r(a) * n_{a c}. \end{aligned}$$

(9)

The integration of network structure into learned embeddings is crucial for capturing the inherent characteristics of a network. In Eq. (8), the numerator represents the maximum link rate of the network, which takes into account the temporal decay of node embeddings. This motivates the combination of network representation learning and the exploration of macroscopic evolutionary patterns in dynamic networks.

Fig. 4

An illustration of a dynamic network exhibits both micro- and macrolevel evolution patterns

As the dynamic network evolves, $A\!\! =\! \left\{ {n_\textrm{e}^{\left( 1 \right) },\;n_\textrm{e}^{\left( 2 \right) },\; \ldots ,\;{n_\textrm{e}}^{\left( T \right) }} \right\}$ represents the number of edges in the dynamic network for T time steps, where ${n_\textrm{e}^{\left( a \right) }}$ is the total number of edges in the network at time up to a. Then, the true number of edges changed in the network at time a is

$$\begin{aligned} \Delta n_\textrm{e}^{\left( a \right) } = n_\textrm{e}^{\left( {a + 1} \right) } - n_\textrm{e}^{\left( a \right) }. \end{aligned}$$

(10)

To capture the macrolevel evolution dynamics of the network, we aim to construct a loss function for the embedding process that preserves these dynamics. At time a, the loss function is determined by minimizing the sum of squared errors between the actual count of changed edges in the network, denoted as $\Delta n_\textrm{e}^{\left( a \right) }$, and the predicted count of changed edges, denoted as $\Delta n_{\textrm{e}}^{\prime (a)}$, which is based on the macroevolution pattern. The formulation is as follows:

$$\begin{aligned} L_{m}^{(a)}=\left( \Delta n_{\textrm{e}}^{(a)}-\Delta n_{\textrm{e}}^{\prime (a)}\right) ^{2}. \end{aligned}$$

(11)

Microscopic and macroscopic representations of dynamic evolution

This paper presents the Bi-DNE model, which integrates micro- and macroevolution dynamics of dynamic networks into DNE. Figure 4 shows a dynamic network diagram that reflects the model’s idea, described as follows:

• Microlevel: From time step a to $a+2$, new edges gradually evolve due to the triadic closure effect of nodes that are not connected but have common friends. Each change is described in detail, reflecting the dynamic characteristics of the network at the microlevel. For example, the triadic closure process of these three adjacent time steps generated a total of four new edges.

• Macrolevel: The number of edges does not change randomly but rather exhibits significant distribution characteristics. This macroevolution dynamic reveals the potential evolution patterns of dynamic networks, which can further constrain the learning of network node representations at a higher level. That is, networks gradually evolve through fine-grained changes and ultimately form a network with a certain size. For example, from time step a to $a+1$, the network generates three new edges through microevolution, while from time step $a+1$ to $a+2$, the network generates only one new edge through microevolution. Observing the parabolic trend in the graph shows that the network generates more edges in the early stages through triadic closures, but the growth rate gradually declines as time passes.

• Micro- and macrolevels combined: The micro- and macrolevels serve as guiding principles for the network evolution and node embedding tasks. The triadic closure process that occurs among the nodes at the microlevel drives the continuous generation of edges. However, this effect is limited by the distribution characteristics at the macrolevel, which jointly determine how many new edges are generated at each time step.

Preservation of dynamic embedding through community structure

In dynamic networks, community structures are important characteristics. Social network groups are represented as data points in an embedding space. Even if they are not directly connected, groups tend to be closer together than individuals from different groups. Measuring the distances between communities helps keep the network structure intact.

Let $C^{(a)} = \left\{ C_1^{(a)},C_2^{(a)},\ldots ,C_m^{(a)}\right\}$ be the set of m community structures in dynamic network G at time step a. For any vertex pair $v_i^{(a)}\in C_p^{(a)}$ and $v_j^{(a)}\in C_q^{(a)}$ $(i\ne j)$, there are four possible edge subsets based on whether nodes have an edge $e_{ij}$ and whether they belong to the same community $p=q$ or different communities $p\ne q$ [17]

• $S_1^{(a)}=\left\{ (v_i, v_j) \mid e_{ij} \in E^{(a)} \bigwedge p=q\right\}$: Linked vertex pair in the same community. [17]

• $S_2^{(a)}=\left\{ (v_i, v_j) \mid e_{ij} \in E^{(a)} \bigwedge p \ne q\right\}$: Linked vertex pair in different communities. [17]

• $S_3^{(a)}=\left\{ (v_i, v_j) \mid e_{ij} \notin E^{(a)} \bigwedge p=q\right\}$: Unlinked vertex pair in the same community. [17]

• $S_4^{(a)}=\left\{ (v_i, v_j) \mid e_{ij} \notin E^{(a)} \bigwedge p \ne q\right\}$: Unlinked vertex pair in different communities. [17]

The proximity between vertex pairs is measured separately for each of the four subsets. The loss function to preserve community structure is formally defined as

$$\begin{aligned} L_{c}^{(a)}=\sum _{\left( i, j\right) \in S^{(a)}} \left[ \xi _{ij}^{(a)}*g^{(a)}(v_i, v_j)\left\| \varvec{u}_{i}^{(a)}- \varvec{u}_{j}^{(a)}\right\| _2^2+\gamma \right] _{+}. \end{aligned}$$

(12)

Let set $S^{(a)}=S_1^{(a)} \cup S_2^{(a)} \cup S_3^{(a)} \cup S_4^{(a)}$ represent all vertex pairs in network G at time a. The Euclidean distance between embeddings of vertices $v_i$ and $v_j$ is denoted as $\left\| \varvec{u}_i^{(a)} - \varvec{u}j^{(a)}\right\| 2^2$. The notation $[x]+$ represents $\max (0,x)$ for a real number x. $\gamma \in \mathbb {R}^+$ is a margin hyperparameter. $\xi {ij}^{(a)}$ is defined in Eq. (2). The function $g^{(a)}(v_i,v_j)$ indicates whether vertices $v_i$ and $v_j$ are linked at time a

$$\begin{aligned} g^{(a)}(v_i,v_j)={\left\{ \begin{array}{ll} 1, &{}\quad \text {if } (v_i,v_j) \in S_1^{(a)} \cup S_2^{(a)}\\ -1, &{}\quad \text {otherwise}, \end{array}\right. }\end{aligned}$$

(13)

where it outputs 1 if $v_i$ and $v_j$ are linked, and -1 otherwise.

Conjunctive model

Dynamic evolution of networks occurs at both micro- and macrolevels and plays a crucial role in their development. We construct an overall objective function that incorporates three loss functions: $L_{c}^{(a)}$ (Eq. (12)) for community structure preservation, $L_{t}^{(a)}$ for microevolution preservation (Eq. (6)), and $L_{m}^{(a)}$ for macroevolution preservation (Eq. (11)). Minimizing these loss functions allows us to capture the intricate dynamics of dynamic networks and obtain meaningful representations for nodes in the network. The formulation is as follows:

$$\begin{aligned} L_{l o s s}=\sum _{a \in T} L_{c}^{(a)}+\beta _{0} L_{t}^{(a)}+\beta _{1} L_{m}^{(a)}, \end{aligned}$$

(14)

where $\beta _0\in [0,1]$ is the weight of the microlevel network evolution pattern on the DNE constraint, and $\beta _1\in [0,1]$ is the weight of the macrolevel network evolution pattern on the DNE constraint.

In this study, the entire training procedure of the Bi-DNE approach discussed above is outlined as Algorithm 1.

Algorithm 1

Overall framework of Bi-DNE

Experiment settings

All methods were implemented using Python 3¹ The hyperparameters involved in this experiment and their meanings are enumerated in Table 5.

Table 5 List of hyperparameters

Dataset

In this study, the proposed model Bi-DNE is evaluated using four real-world dynamic networks, which are described as follows:

• The fb-messages network [45]: This dataset represents an online community of 1,899 students from the University of California, Irvine. It includes 59,835 messages sent between them from April to October 2004.

• The ia-facebook network [45]: This dataset shows the connections between 44,686 users over 24 months. A total of 735,439 links that were recorded between 2007 and 2008. Earlier data were not included due to lack of information.

• The ia-contacts-Dublin network [45]: This network consists of daily dynamic contacts collected during the Infectious Social Patterns event at the Science Gallery in Dublin, Ireland, during the ArtScience Exhibition. The data were collected at 20-s intervals. The network spans ten time steps, with each time step representing a 3-week period.

• The ia-retweet-pol network [45]: This dataset includes 470 Twitter users as vertices and 61,157 retweet relations as edges. It spans six time steps, with each step representing a three-week period.

Figure 5 presents more detailed statistics concerning the experimental data.

Fig. 5

The statistics of four datasets. From left to right are: fb-messages, ia-facebook, ia-contacts, and ia-retweet

Baseline

To evaluate the effectiveness of the suggested model, we have chosen five baseline methods. These methods include three SNE techniques (DeepWalk, Node2vec, and LINE) and two DNE methods (TNE and DynamicTriad). To ensure fair comparisons in our experiments, we have carefully chosen the best settings for each of the baseline algorithms by tuning their parameters.

To evaluate the effectiveness of the suggested model, we choose five baseline methods for comparison purposes. These methods include three SNE techniques (DeepWalk, Node2Vec, and LINE) and nine DNE methods (TNE, DynamicTriad, AGA, GDM, TFIP, DGCN, DynamiSE, ERM-ME, and DINE). To ensure fair comparisons in our experiments, we carefully select the best settings for each of the baseline algorithms by tuning their parameters.

• DeepWalk (2014) [20] is a widely used approach to embed static networks. It leverages truncated random walks to capture vertex structural information and generates low-dimensional vector representations for each vertex. Close vertices in the random walk sequence are assumed to be similar. Our DeepWalk experiments used a step size of 8, a window size of 5, and 100 steps per vertex.

• Node2vec (2016) [22] is a model that improves neighbor selection during random walks by introducing hyperparameters p and q. This results in better node representation. It also uses a skip-gram graph model and has similar step and window size settings as DeepWalk. We set $p=0.15$ and $q=4$ in our experiments.

• LINE (2015) [23] is a method that captures the first-order similarity between directly connected nodes, preserving local information in the network. It also introduces second-order similarity for nodes with familiar neighbors, capturing global network information. By integrating these two similarity measures, LINE models the relationships between nodes and obtains node representations as embedding vectors.

• TNE (2016) [12] is a matrix factorization algorithm for DNE that captures temporal changes. We used its default parameters in our experiments.

• DynamicTriad (2018) [35] studies changing networks by analyzing triads. The settings in our experiments are the same as Yang et. al [17].

• AGA (2021) [30] introduced a budget-constrained optimization module, and achieved superior accuracy on many paths. The hyperparameter $\beta$ is set to 1.

• GDM (2021) [31] is a static network embedding method combined with a Gaussian propagation model. We used its default parameters in our experiments.

• TFIP (2022) [46] uses sentiment analyzing methods to embedding static network. The active probability in TFIP is set as 0.1.

• DGCN (2022) [41] is a dynamic network embedding model applying GCN modules. The number of hidden layers is set to 2, the hidden layer size is set to 128, and the number of convolutional layers is set to 2.

• DynamiSE (2023) [42] is a model that simultaneously encodes the dynamics and symbolic semantics of the network for link prediction. The search range is set to 0.001, 0.01, 0.1, 0, 1, 10, 100.

• ERM-ME (2022) [43] is a dynamic network embedding method to capture the attributes and emotions of different roles in social networks. The parameters that control the iteration are the same as Du et al. [43].

• DINE (2023) [44] is a network node dynamic embedding model for social recommendation. The batch size is set as 512 and the dimension of embedding d is set as 24. The learning rate and the regularization coefficient are searched in [0.0001, 0.0005, 0.001, 0.0057] and [0.0001, 0.001, 0.01, 0.1], respectively.

Parameter setting

Prior to learning the network representation, a comprehensive examination of different parameter combinations is conducted to identify the optimal control parameters. The main parameters considered in this study are $\eta \in \left\{ 0.1,0.3,0.5,0.7,0.9 \right\}$, $\alpha \in \left\{ 0.3,0.4,0.5,0.6,0.7,0.8 \right\}$, and $\gamma \in \left\{ 0,1,2,3,4 \right\}$, which are tested with values from predefined sets.

The Bi-DNE model and the baselines are used to obtain embedding vectors for nodes via network representation learning. Subsequently, the positive and negative samples acquired at various time steps are collected, and a logistic regression model is utilized as the classifier. The collected samples are subjected to fivefold cross-validation, and the experiments are repeated ten times to assess the performance of the tested methods. Experimental comparisons are then conducted based on the averaged results.

To determine the most suitable dimension for the latent vector space, different values of $d =\left\{ 24, 48, 72, 96, 120 \right\}$ are tested. For performance comparison, we chose embedding vector dimension $d=48$ after weighing computational complexity and performance.

Evaluate tasks and benchmarks

Bi-DNE learns low-dimensional vertex representations, which are applied to graph-related tasks, including link reconstruction, prediction, and modification. In this study, the embedding vectors of vertices are used to create feature representations for network edges. The feature representation for each edge is formulated as $\;{e_{ij}} = \left| {{u_i} - {u_j}} \right|$.

• Link prediction: The objective of link prediction in dynamic networks is to predict the presence of future edges within the network. In DNE, low-dimensional representations $\varvec{u}_i^{(a)}$ and $\varvec{u}j^{(a)}$ of vertices $v_i$ and $v_j$ at time a are used to predict the existence of an edge e ij between them at time $a+1$. Link prediction is done by using vertex embeddings to estimate connection likelihoods. The embedding vectors of nodes can express the likelihood of connections between them.

• Link reconstruction: Link reconstruction is a method for testing the effectiveness of NEs by analyzing the spatial positions of the embedding vectors assigned to two vertices and determining their presence or absence. The relative positioning of two nodes in the embedding space reflects whether they share a connection.

• Dynamic link prediction and reconstruction: This work studies how dynamic networks predict and reconstruct changes in their edges, which greatly affect their overall development over time. By analyzing these changes, we can better understand the network’s dynamic qualities at different points in time. The network connections are assumed to be dynamic and evolving, with new links forming based on mechanisms like triadic closure.

Link prediction and reconstruction are fundamental components that assess if embeddings effectively encode the presence or absence of edges. Dynamic link prediction and reconstruction, on the other hand, specifically evaluate how well embeddings handle network evolution over time. The problem suite assesses whether Bi-DNE achieves this objective. To assess the Bi-DNE’s effectiveness, we consider precision, recall, and F1-score as performance metrics.

Results

This section includes experiments conducted on four datasets using our proposed model Bi-DNE and several baseline models. We evaluate the performance of the learned embedding vectors through four downstream tasks: link reconstruction, link prediction, and joint link reconstruction and prediction. The statistical values obtained from these experiments are recorded in Table 6 and Figs. 6, 7, 8, 9, with the best results highlighted in bold.

Table 6 The F1-score of Bi-DNE and the baselines exhibited on four datasets

Fig. 6

Comparison of F1-scores for all algorithms across fb-messages dataset and downstream tasks

Fig. 7

Comparison of F1-scores for all algorithms across ia-facebook dataset and downstream tasks

Fig. 8

Comparison of F1-scores for all algorithms across ia-contacts-Dublin dataset and downstream tasks

Fig. 9

Comparison of F1-scores for all algorithms across ia-retweet-pol dataset and downstream tasks

Our research shows that the Bi-DNE algorithm performs better than the other baseline algorithms in most cases. The comparison among the F1 scores achieved by Bi-DNE and the other baselines across the four downstream tasks conducted on the fb-messages, ia-facebook, ia-contacts, and ia-retweet-pol datasets is shown in Figs. 6, 7, 8, and 9. It is noteworthy that Bi-DNE outperforms the other algorithms by achieving the best statistical F1 scores in 12 out of 16 tests. These results serve as compelling evidence for the effectiveness and superiority of our algorithm.

The experimental results lead to several key conclusions regarding the six network representation learning methods used in this study, which are categorized into static and dynamic models. The following findings are observed:

These findings demonstrate the superior performance of Bi-DNE, which effectively combines both micro- and macrolevel network characteristics. The model outperforms other approaches in terms of various tasks and datasets, showcasing its strength as a comprehensive and robust network representation learning method.

• (1) Our proposed models, Bi-DNE, DynamicTriad, and TNE, along with other DNE methods, are found to outperform SNE methods such as DeepWalk, LINE, and Node2Vec. This suggests that accounting for the dynamic characteristics of a network along with its topological structure properties during the embedding process can yield an improved network representation learning effect.

• (2) Out of the three methods for DNE, Bi-DNE and DynamicTriad have shown to perform the best. These models are able to capture the microlevel evolution trend and fine-grained structural properties of the network by modeling the triadic closure process. They also create representation vectors for each vertex step, which shows how effective it is to incorporate the ternary closure principle in the DNE process. However, TNE has suboptimal performance with sparse network adjacency matrices due to imbalanced samples.

• (3) Building upon the modeling of the dynamic network evolution process at the microlevel, Bi-DNE further incorporates the macrolevel evolution pattern to encode high-level structures in the embedding space. This additional feature enhances the performance of the model, making Bi-DNE stand out from the other approaches. Our model achieves the best results in three tasks (all except for link prediction) across various datasets.

In addition, the four downstream tasks can be classified into generic tasks and dynamic tasks. The comparisons drawn from our analysis reveal the following key findings: In tasks that require constant change, Bi-DNE has proven to show a considerable improvement in performance. When compared to the baseline model that obtained the highest F1-score on the four datasets for the altered link reconstruction task, Bi-DNE has shown a significant gain of 51.2%, 38.8%, 41.9%, and 32.8%, respectively. Similarly, the Bi-DNE model outperformed the baseline in predicting changed links, with F1 scores and improvements up to 55.8%. It adapts to dynamic networks by capturing changing trends at micro- and macrolevels, successfully preserving evolutionary patterns. Our proposed model is a suitable solution for addressing the needs of dynamic networks. Finally, we analyzed the datasets of four real networks used in the experiment, and the trend of edge changes is shown in Fig. 10:

Fig. 10

The trend of edge changes in the four datasets

By carefully observing the network dynamics over time, several noteworthy insights can be gleaned:

• First, the fb-messages dataset exhibits a distinct downward trend in edge changes, with the disappearance of edges outweighing the generation of new edges. This pattern indicates a substantial loss of connections within the network.

• Second, ia-facebook emerges as a prototypical social network, characterized by a high frequency of evolutionary trends commonly observed in real-life social networks. This dataset, therefore, serves as a valuable reference for experimental analysis, given its relevance to the dynamics of social networks.

• Third, the ia-contacts dataset displays a relatively small range of edge changes. This dataset represents a unique scenario where the generation and disappearance of edges resulting from triadic closure processes are roughly balanced.

• Finally, in the ia-retweet-pol dataset, edges demonstrate a gradual and steady growth rate during the initial two moments, followed by a stable phase with minimal changes. Leveraging the principles of ternary closure theory and dense power law, our research successfully captures the dynamic process of edge generation and the overall network growth scale. Consequently, our approach achieves optimal results in networks where the rate of edge growth intensifies, such as ia-facebook, which exemplifies the typical dynamics of social networks.

We performed ablation experiments on four datasets to investigate the effect of various modules of this paper on the model’s final performance. Table 7 and Fig. 11 present the experimental results, which indicate varying degrees of influence on Bi-DNE’s performance from the microlevel structure, macrolevel structure, and community structure. The research shows that embeddings with community structure combined with the removal of macrolevel dense power laws have the greatest influence on Bi-DNE and can enhance the quality of low-dimensional vectors. The modules that combine both macro- and microlevels play a critical role in this process. When comparing the ablation experiment of micro- and macrostructure, we found that the performance of microdense power law decreases more when the macroternary closure rule is removed. This indicates that the macrolevel is the most important in the module that combines macro and micro. From another perspective, both the microlevel and the community structure effectively improve the performance of the triadic closure model. However, the results obtained by only using community structure are not satisfactory, indicating that relying solely on community structure is insufficient for understanding the evolution of social networks. In the experiments conducted on the four data sets, the effect of the changing link task was better, indicating that our method is better at dealing with dynamically changing network characteristics compared to a static network.

Table 7 The F1 values of the Bi-DNE model ablation experiments on the four datasets

Fig. 11

Ablation experimental results of Bi-DNE on four datasets

Conducting a sensitivity analysis on the utilized parameters is a crucial aspect of research, as it aids in comprehending the extent of influence that parameters have on study outcomes and assessing the soundness of parameter selection. The Bi-DNE algorithm encompasses five primary hyperparameters: (1) $\alpha$, responsible for controlling community influence, (2) $\gamma$, determining the boundary value of the loss function for community structure information, (3) d, representing the vector dimension, (4) $\beta _0$, denoting the weight of microlevel network evolution pattern on DNE constraint, and (5) $\beta _1$, denoting the weight of macrolevel network evolution pattern on DNE constraint. The range for the parameter $\alpha$ was set to $\left\{ 0.3, 0.4, 0.5, 0.6, 0.7, 0.8 \right\}$. The parameter $\gamma$ was tested with values $\left\{ 1, 2, 3, 4\right\}$. The parameter d with values $\left\{ 24, 48, 72, 96, 120\right\}$, $\beta _0$ with $\left\{ 0.01,0.1,0.2,0.3,0.4,0.5\right\}$, $\beta _1$ with $\left\{ 0.01,0.1,0.2,0.3,0.4,0.5\right\}$. These experiments were conducted using the fb-message and ia-retweet-pol datasets.

Figure 12 illustrates the results obtained when analyzing the $\alpha$ parameter. It is evident that the performance of Bi-DNE improves across all four tasks as $\alpha$ increases up to a certain threshold. Notably, when $\alpha$ is set to 0.5, our model fails to differentiate whether network vertices belong to the same community. However, as $\alpha$ continues to increase, specifically reaching 0.6, Bi-DNE takes the community structure information into account. This consideration results in a significant increase in the F1 value, indicating that incorporating community structure information proves advantageous for enhancing the performance of the network embedding process.

Fig. 12

Statistical performance of Bi-DNE with different alpha value

The experimental findings depicted in Fig. 13 showcase the varying performance of Bi-DNE across different values of $\gamma$. The outcomes illustrate a gradual enhancement in the F1 score for all four tasks as $\gamma$ increases from 0 to 1. Nevertheless, as $\gamma$ continues to escalate, the model’s performance stabilizes, suggesting its robustness to this parameter.

Fig. 13

Statistical performance of Bi-DNE with different gamma value

The experimental results captured in Fig. 14 portray the evolving performance of Bi-DNE in terms of the F1 scores with respect to the embedding dimension d. The findings reveal a progressive enhancement in Bi-DNE’s performance across the four tasks as d increases from 24 to 96. However, the improvements become marginal upon further increase in the d value, as a substantial portion of the essential information has already been captured within the embedding vectors. To strike a balance between computational resources and Bi-DNE’s performance, this study sets the number of dimensions to 48.

Fig. 14

Statistical performance comparison of Bi-DNE with different values of d

The analysis conducted on the $\beta _0$ parameter, with a fixed value of 0.01, is depicted in Fig. 15. Notably, the model’s F1 index scores exhibit variations ranging from 0.003 to 0.009 for the fb-facebook dataset, and 0.002 to 0.013 for the ia-retweet-pol dataset. In Fig. 16, the analysis focuses on the $\beta _1$ parameter, while maintaining a fixed value of $\beta _0$=0.1. The model’s F1 index scores display variations ranging from 0.012 to 0.029 for the fb-facebook dataset, and 0.024 to 0.088 for the ia-retweet-pol dataset. These findings clearly indicate that the proposed model demonstrates consistent performance even when the $\beta _0$ and $\beta _1$ parameters are adjusted. Hence, it can be concluded that the Bi-DNE model exhibits robustness in relation to these two primary model parameters.

Fig. 15

Statistical performance of Bi-DNE with different $\beta _0$

Fig. 16

Statistical performance of Bi-DNE with different $\beta _0$

Complexity and overhead analysis

Based on the analysis of the Bi-DNE algorithm in the section “Framework of Bi-DNE model”, we can conclude that the algorithm automatically updates coupling coefficients through multiple iterations to obtain part-whole relationships. The algorithmic complexity of Bi-DNE can be seen as the summation of embedding complexities from the microlevel module, macrolevel module, and community structure module. In this process, we assume the number of nodes as n, the embedding dimension as d, and the number of edges as l. The required training time per round for our proposed model is 740 seconds, while Deepwalk is 95 seconds and DynamicTraid is 702 seconds. We compared Bi-DNE with DynamicTriad, another triadic closure-based model, and classic representation learning algorithms DeepWalk and Node2Vec. With a microlevel complexity of $O(n^3)$ utilizing triadic closure, macrolevel complexity of O(nd), and community structure complexity of O(nd), the overall complexity of Bi-DNE is $O(n^3+2nd)$, which is still $O(n^3)$. DynamicTriad performs well on link prediction tasks and has an $O(n^3)$ worst-case complexity. DeepWalk and Node2Vec require additional consideration of walk times, thus having an overall split complexity of $O(nd+nl)$ for walks and embedding. Finally, based on the dataset attributes in this paper, the complexity of Bi-DNE and DynamicTriad is $O(n^3)$. At the same time, the classic network embedding algorithms like DeepWalk and Node2Vec have a complexity of $O(n^2)$. The running time of the three algorithms is in line with the complexity of their respective algorithms. While both Bi-DNE and DynamicTraid have an $O(n^3)$ complexity, Bi-DNE also takes into account the community structure and dense power-law overhead, resulting in a slightly longer running time compared to the DynamicTraid method.

Real-world feasibility analysis

The paper uses real-world datasets, which allows the proposed model to demonstrate its excellent performance in practical applications. Although Bi-DNE may be more computationally complex than traditional static network embedding models, it is still feasible with modern computing resources. The advantage of Bi-DNE over traditional models is its ability to effectively capture the evolutionary process of a network over time, which is invaluable in many practical applications. As a dynamic network embedding model with superior performance, Bi-DNE is suitable for real-time or near-real-time analysis tasks, such as social media trend analysis. To successfully implement the Bi-DNE model in real-world scenarios, it is first necessary to collect high-quality dynamic network datasets and perform necessary preprocessing work, such as denoising and normalization, to ensure the quality of the input data. Additionally, appropriate model parameters, such as the community influence coefficient and learning rate, should be selected for performing accurate tuning according to actual business needs. Cloud computing platforms can also be used to deploy model services to ensure high availability, low latency, and service scalability. Finally, continuous model monitoring, evaluation, and update mechanisms should be established to ensure the stability and continuous improvement of the model performance. After conducting pretraining with data from different fields, our proposed method can also be applied to user profiling and recommendation in social networks, abnormal transaction detection in financial networks, and traffic flow prediction.

Conclusion

In this paper, we analyze the evolution of networks on both a micro- and macrolevel. At the microlevel, nodes in the network dynamically form their structure based on the triadic closure principle. Meanwhile, the number of edges in the network on a macrolevel follows a power-law distribution that determines the scale of network evolution. Based on these insights, we introduce the integration of triadic closure and dense power-law concepts into network representation learning. To address this important problem, a novel dynamic network representation learning model called Bi-DNE is proposed. The model captures the process of network structure formation through a strengthened triadic closure mechanism at the microlevel. Additionally, a dynamic equation ensures that the network structure adheres to the dense power-law evolution pattern at the macrolevel. To further enhance the quality of network embedding, the model incorporates community structure, enabling the extraction of richer information from the network. To assess the effectiveness of the proposed model, a comprehensive evaluation is conducted on four real-world datasets, encompassing diverse tasks, such as link prediction, link reconstruction, changed link prediction, and reconstruction. The experimental findings consistently demonstrate that the Bi-DNE framework adeptly captures the dynamic evolution information, providing robust evidence of its effectiveness and practical utility.

In this paper, we analyze the evolution processes of networks at both the micro- and macrolevels. At the microlevel, the nodes in a network dynamically form their structure based on the triadic closure principle. Furthermore, the number of edges in the network at the macrolevel follows a power-law distribution that determines the scale of network evolution. Based on these insights, we integrate the triadic closure and dense power-law concepts into the network representation learning process. To address this important problem, a novel dynamic network representation learning model called Bi-DNE is proposed. The model captures the network structure formation process through a strengthened triadic closure mechanism at the microlevel. Additionally, a dynamic equation ensures that the network structure adheres to the dense power-law evolution pattern at the macrolevel. To further enhance the quality of network embeddings, the model incorporates community structure information, enabling the extraction of richer information from the network. To assess the effectiveness of the proposed model, a comprehensive evaluation is conducted on four real-world datasets, encompassing diverse tasks, such as link prediction, link reconstruction, changed link prediction, and reconstruction. The experimental findings consistently demonstrate that the Bi-DNE framework adeptly captures dynamic evolution information, providing robust evidence of its effectiveness and practical utility.