Abstract
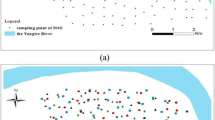
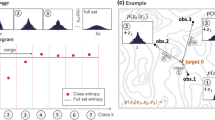
This study proposes the method of simulating spatial patterns and quantifying the uncertainty in multivariate distribution of heavy metals (Cr, Cu, Ni, and Zn) by sequential indicator simulation (SIS) combined with conditional Latin hypercube sampling (cLHS) in Changhua County, Taiwan. The cLHS is used for a sampling then for SIS mapping and assessing uncertainties of heavy metal concentrations. The indicator variogram results indicate that the 700 cLHS samples replicate statistical multivariate distribution and spatial structure of the 1,082 samples. Moreover, the SIS realizations based on 700 cLHS samples are more conservative and reliable than those based on 1,082 samples for delineating soil contamination by all heavy metals with the exception of Zn. Given adequate sampling, soil contamination simulation provides sufficient information for delineating contaminated areas and planning environmental management.









Similar content being viewed by others
References
Amini M (2005) Mapping risk of cadmium and lead contamination to human health in soils of Central Iran. Sci Total Environ 347(1–3):64–77
Bourennane H, King D, Couturier A, Nicoullaud B, Mary B, Richard G (2007) Uncertainty assessment of soil water content spatial patterns using geostatistical simulations: an empirical comparison of a simulation accounting for single attribute and a simulation accounting for secondary information. Ecol Model 205:323–335
Carre F, McBratney AB, Minasny B (2007) Estimation and potential improvement of the quality of legacy soil samples for digital soil mapping. Geoderma 141(1–2):1–14
Castrignano A, Buttafuoco G (2004) Geostatistical stochastic simulation of soil water content in a forested area of South Italy. Biosyst Eng 87:257–266
Castrignanò A, Cherubini C, Di Mucci G, Giasi CI, Molinari M (2004) The application of spatial modelling of the variability for the interpretation of a case regarding arsenic pollution in groundwater. Integrated methods for assessing water quality. 21–22 October, Louvain–La-Neuve, Belgium
Cherubini C (2009) A geostatistically based probabilistic risk assessment approach. In: Evolving application domains of data warehousing and mining: trends and solutions. Igi Global Publisher Idea Group Inc. ISBN: 978-1-60566-816
Cherubini C, Musci F, Pastore N (2009) Stochastic geolithological reconstruction coupled with artificial neural networks approach for hydrogeological modeling. Int J Math Models Methods Appl Sci 2(3), ISSN: 1998-0140
Deutsch CV, Cockerham PW (1994) Practical considerations in the application of simulated annealing to stochastic simulation. Math Geol 26(1):67–82
Deutsch CV, Journel AG (1992) GSLIB: geostatistical software library and user’s guide. Oxford University Press, New York, p 340
Fortin MJ, Edwards G (2001) A cognitive view of spatial uncertainty. In: Hunsaker CT, Goodchild MF, Friedl MA, Case TJ (eds) Spatial uncertainty in ecology: implications for remote sensing and GIS applications. Springer, New York, pp 133–157
Franco C, Soares A, Delgado J (2006) Geostatistical modelling of heavy metal contamination in the topsoil of Guadiamar river margins (S Spain) using a stochastic simulation technique. Geoderma 136(3–4):852–864
Goovaerts P (1996) Stochastic simulation of categorical variables using a classification algorithm and simulated annealing. Math Geol 28:909–921
Goovaerts P (1999) Geostatistics in soil science: state-of-the-art and perspectives. Geoderma 89(1–2):1–45
Goovaerts P (2001) Geostatistical modelling of uncertainty in soil science. Geoderma 103(1–2):3–26
Hassan MM, Atkins PJ (2007) Arsenic risk mapping in Bangladesh: a simulation technique of cokriging estimation from regional count data. J Environ Sci Health Part A Toxic Hazard Subst Environ Eng 42(12):1719–1728
Iman RL, Conover WJ (1980) Small sample sensitivity analysis techniques for computer-models, with an application to risk assessment. Commun Stat Part A Theory Methods 9(17):1749–1842
Journel AG (1996) Modelling uncertainty and spatial dependence: stochastic imaging. Int J Geogr Inform Sci 10(5):517–522
Juang KW, Chen YS, Lee DY (2004) Using sequential indicator simulation to assess the uncertainty of delineating heavy-metal contaminated soils. Environ Pollut 127(2):229–238
Kyriakidis PC (2001) Geostatistical models of uncertainty for spatial data. In: Hunsaker CT, Goodchild MF, Friedl MA, Case TJ (eds) Spatial uncertainty in ecology: implications for remote sensing and GIS applications. Springer, New York, pp 175–213
Lin YP (2002) Multivariate geostatistical methods to identify and map spatial variations of soil heavy metals. Environ Geol 42:1–10
Lin YP (2008) Simulating spatial distributions, variability and uncertainty of soil arsenic by geostatistical simulations in Geographic information systems. Open Environ Sci 2:26–33
Lin YP, Chang TK, Teng TP (2001) Characterization of soil lead by comparing sequential Gaussian simulation, simulated annealing simulation and kriging methods. Environ Geol 41(1):189–199
Lin YP, Chang TK, Shi CW, Tsen CH (2002a) Factorial and indicator kriging method using geographic information system to delineate spatial variation and pollution sources of soil heavy metals. Environ Geol 42:900–909
Lin YP, Teng TP, Chang TK (2002b) Multivariate analysis of soil heavy metal pollution and landscape pattern in Changhua County in Taiwan. Landsc Urban Plan 62(1):19–35
Lin YP, Yeh MS, Deng DP, Wang YC (2008) Geostatistical approaches and optimal additional sampling schemes for spatial patterns and future sampling of bird diversity. Glob Ecol Biogeogr 17:175–188
Lin YP, Cheng BY, Shyu GS, Chang TK (2010) Combining a finite mixture distribution model with indicator kriging to delineate and map the spatial patterns of soil heavy metal pollution in Chunghua County, Central Taiwan. Environ Pollut 158(1):235–244
McKay MD, Beckman RJ, Conover WJ (1979) Comparison of 3 methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 21(2):239–245
Minasny B, McBratney AB (2006) A conditioned Latin hypercube method for sampling in the presence of ancillary information. Comput Geosci 32(9):1378–1388
Pachepsky Y, Acock B (1998) Stochastic imaging of soil parameters to assess variability and uncertainty of crop yield estimates. Geoderma 85:213–229
Saito H, Goovaerts P (2000) Geostatistical interpolation of positively skewed and censored data in a dioxin-contaminated site. Environ Sci Technol 34(19):4228–4235
Schnabel U (2004) Uncertainty assessment for management of soil contaminants with sparse data. Environ Manage 33(6):911–925
Van Meirvenne M, Goovaerts P (2001) Evaluating the probability of exceeding a site-specific soil cadmium contamination threshold. Geoderma 102(1–2):75–100
Xu CG, He HS, Hu YM, Chang Y, Li XZ, Bu RC (2005) Latin hypercube sampling and geostatistical modeling of spatial uncertainty in a spatially explicit forest landscape model simulation. Ecol Model 185(2–4):255–269
Zhao YC, Shi XZ, Yu DS et al (2005) Uncertainty assessment of spatial patterns of soil organic carbon density using sequential indicator simulation, a case study of Hebei Province, China. Chemosphere 59(11):1527–1535
Zhao Y, Xu X, Sun W et al (2008) Uncertainty assessment of mapping mercury contaminated soils of a rapidly industrializing city in the Yangtze River Delta of China using sequential indicator co-simulation. Environ Monit Assess 138:343–355
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lin, YP., Chu, HJ., Huang, YL. et al. Modeling spatial uncertainty of heavy metal content in soil by conditional Latin hypercube sampling and geostatistical simulation. Environ Earth Sci 62, 299–311 (2011). https://doi.org/10.1007/s12665-010-0523-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12665-010-0523-5